基于粗糙集属性依赖度强化的交互式大数据特征分类

曹夏琳

(厦门海洋职业技术学院 信息工程学院, 福建 厦门 361000)

由于大多数数据的存储、选择和计算等都是以小型数据为基础[1],无法发现数据背后的秘密,随着数据量的增多,无法及时地解决用户的需要[2].因此,需要对大数据进行特征分类.交互式大数据的特征分类是从大量的、看起来很复杂的和没有规律的数据集合中,提取出隐藏的、未被发现的和具有现实意义的数据特征,这个分类的过程十分重要[3].传统的大数据特征分类基于决策树的方法,通过预处理数据并对其进行总结,从而获得可能的类型,为科研工作者提供决策依据.在这个高信息量的大环境下,对交互式大数据进行特征分类成为一种不可或缺的技术.

李越颖[4]提出了一种新的基于相邻搜索技术的实时数据抽取技术,用来解决现阶段对于海量大数据处理效率低下的问题.首先利用邻域搜索法,对大数据的特征进行分类,然后利用萤火虫算法,对分类后的大数据信息进行优化,获取大数据最优特征集,结合模拟退火算法,完成对数据向量机的内核分类,实验结果表明,该方法具有较高的准确率和召回率.张文杰等[5]利用基因方法,研究了一种新的大数据特征提取方法.首先对大数据的各个维度属性进行评价,并通过各个属性之间的差别来调节其权值,并利用属性权值来指导遗传算法的检索,从而提高了算法的检索性能和提取的精确性.在此基础上,根据属性加权求出了各属性的相似性,以适合性为评估标准,利用遗传算法对所选取的最佳特征集进行优化,从而达到了较好的效果.实验结果表明,该方法可以提升大数据特征分类的准确性.

基于以上研究背景,本文通过强化粗糙集属性依赖度,设计一种交互式大数据特征分类方法,有利于网络中交互式大数据的综合管理.

1 交互式大数据特征分类方法设计

1.1 强化交互式大数据粗糙集属性依赖度

利用粗糙集对交互式大数据进行处理过程中,首先需要对交互式大数据进行处理,将其表示为一个四元组,即

C={D,S,U,K},

(1)

其中D={d1,d2,…,dn}为交互式大数据在粗糙集的属性集合,S={s1,s2,…,sc,sd}为交互式大数据在粗糙集的特征集合,U={u1,u2,…,uc}为交互式大数据在粗糙集的属性值,K={k11,k12,…,knd}为交互式大数据在粗糙集的交互函数,通过交互函数,可以判断交互式大数据在粗糙集上的属性值.

利用交互式大数据在粗糙集的属性依赖度,来确定交互式大数据属性之间的关联关系[6],将依赖程度表示为

其中Gs(Sa,Sb)为交互式大数据属性Sa相对于属性Sb的依赖程度,Za(b)表示交互式大数据的关联系数.

根据交互式大数据的四元组C,给出交互式大数据在粗糙集的属性约束条件Ck,并通过约束条件,将属性集S划分成条件属性集A与决策属性集B[7].通过确定属性Sa∈A对于决策属性Sb∈B的依赖程度,计算Sa在粗糙集上属性依赖度,得到交互式大数据的最小属性依赖度Ω,当交互式大数据与最小属性依赖度的关联性较差时,说明该属性较重要,反之较次要.

利用交互式大数据在粗糙集的近似集,对粗糙集进行模糊处理[8],使得Sa的变化对于交互式大数据在粗糙集上依赖度的影响更加精准.那么交互式大数据在粗糙集上的近似集定义为

其中J(x)为交互式大数据与D关联关系,X为交互式大数据在粗糙集的决策集合,φ为权值,φ∈[0,1],当φ=0时,得到的近似值是准确的,当φ=1时,则会将所有的x纳入交互式大数据在粗糙集的近似集.所以φ越小,最终的结果越准确.

强化交互式大数据粗糙集属性依赖度的过程如图1所示.

图1 强化交互式大数据属性依赖度的过程

根据图1的过程,建立交互式大数据在粗糙集上不同条件属性Sa之间的依赖度关系,结合属性组合对交互式大数据进行重组,使得重要属性依赖度参与交互大数据特征提取的每个部分,得到条件属性Sa关于Sb的依赖度.

1.2 提取交互式大数据特征

在提取交互式大数据特征时,以交互式大数据强化后的粗糙集属性依赖度为依据[9],得到交互式大数据状态量幅值规律,表示为

其中gm为交互式大数据的时间序列,tj为不同交互式大数据的周期性变化时间,K为交互式大数据的类型,f为响应函数,χb为交互式大数据的变化规律,εr为交互式大数据的延迟算子.

考虑到交互式大数据数量巨大和种类繁多,数据之间的密度较大[10],为了保证交互式大数据特征提取的精准性,计算出交互式大数据之间的密度值,公式为

其中Kn为交互式大数据的类别数量,M为交互式大数据的属性数量,Nk为第k类交互式大数据的个数,g(r)为交互式大数据的密度函数,可以利用下式表示

其中Qr表示交互式大数据第r种属性,sims表示交互式大数据之间的相似度,f(s)表示交互式大数据的匹配函数,cr表示交互式大数据的误差值.

交互式大数据数据特征提取方式是实现交互式大数据特征准确分类的基础[11],提取的交互式大数据特征不仅要保证原有数据的特征,还要具有相同类别间的不变特性[12],利用下式可以确定交互式大数据分布的集中区域,即

其中ρk代表交互式大数据的聚类密度,ωg代表交互式大数据的权值向量.

在数据分布密集的区域,由于海量大数据的质量混杂,大量的数据不一致,这就导致了数据特征提取的困难大[13],因此,需要设置特征提取窗口,表示为

其中ηx代表交互式大数据的样本值,lz为特征提取窗口的置信度,Ey代表窗口的大小.

利用公式(8)设置的窗口,提取出交互式大数据的特征,将其定义为

其中n代表交互式大数据特征种类数目,q代表交互式大数据特征提取窗口大小,N*代表交互式大数据特征提取样本数量.

根据交互式大数据状态量的幅值规律,计算出交互式大数据之间的密度值,通过确定交互式大数据分布的集中区域,提取出交互式大数据的特征.

1.3 设计交互式大数据特征分类算法

基于上述数据特征的提取结果,设计了大数据特征分类的决策树算法,表示为

R(x)=I(fk(x)×z),

(10)

其中fk(x)代表交互式大数据的决策模型,z为决策树算法的分类结果,I(·)为特征提取因子.

在交互式大数据中,使用粗糙集属性依赖度对每棵决策树的数据特征进行提取,整个过程需要独立完成.因此使用该算法能够优化交互式大数据的特征分类,提高计算效率和最终的准确度.

如果让决策树拥有良好的交互式大数据提取性能,首先完成交互式大数据的样本训练,获得决策树模型[14].随后获取交互式大数据特征分类的目标函数,定义为

其中e为交互式大数据特征的维度,ei代表特征i在交互式大数据特征中的维度,ej代表特征j在交互式大数据特征中的维度,Uij代表特征i和特征j在交互式大数据中的特征函数.

根据交互式大数据特征分类的目标函数,计算出大数据R的期望熵值,即

其中δi代表交互式大数据中第i个提取特征的概率.

利用交互式大数据R的期望熵值[15],可以得到交互式大数据特征Z的增益信息值R,即

Gaim(R,Z)=E(R)-E(R,Z),

(13)

其中E(R,Z)代表交互式大数据特征Z完成属性分类后的期望熵值.

利用交互式大数据特征的增益信息,设计交互式大数据特征分类算法,对交互式大数据特征进行分类,表示为

其中Vd表示交互式大数据特征值,Σ是n个分类数目,Fsym表示交互大数据特征的分类结果,Wv表示第v个交互式大数据特征矩阵.

通过定义交互式大数据特征分类的目标函数,计算出大数据的期望熵值,利用交互式大数据特征的增益信息值,设计了交互式大数据特征分类算法.

2 实验分析

2.1 实验数据集

为了验证文中方法在实际应用中的有效性,本文选择5组交互式大数据样本集作为实验数据,具体如表1所示.

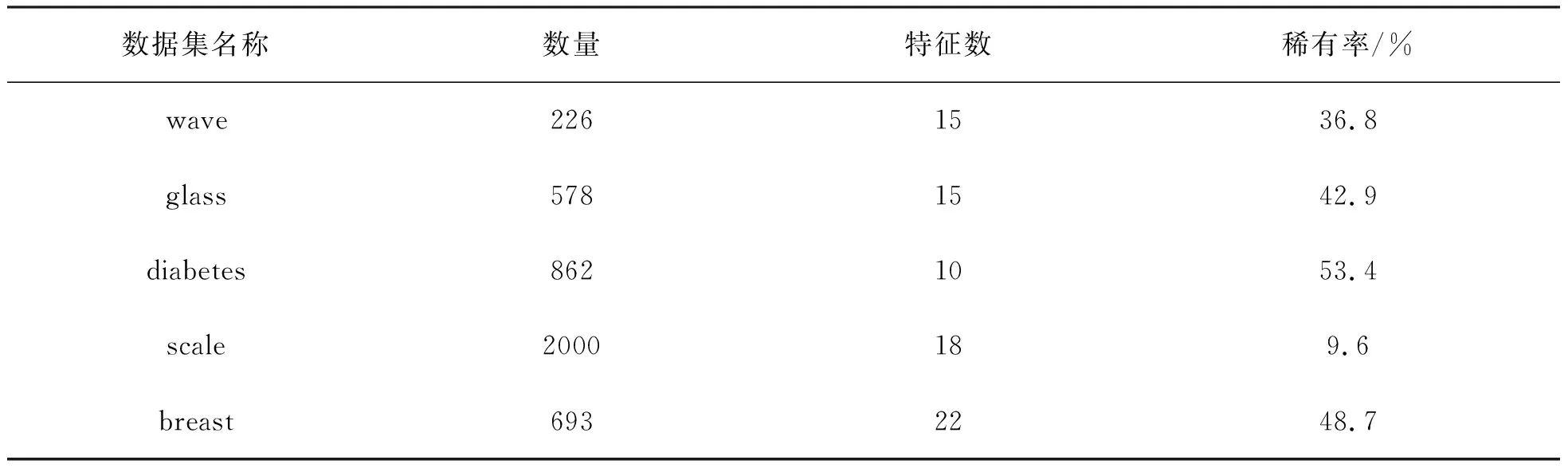
表1 实验数据集信息

2.2 实验环境

本文的实验选择四台机器,一台用作主节点,三台用作工作节点,实验环境的部署为节点内存:4GB;Hadoop版本:Hadoop2.6.0;jdkk编程版本:jdk1.8.2_88;操作系统:Windows 7;Eclipse版本:Eclipse4.6.2.

2.3 挖掘交互式大数据特征

在2.2的实验环境下,挖掘交互式大数据的特征.考虑到交互式网络环境比较复杂,存在很多依赖度偏低的属性,无法从大数据决策矩阵中挖掘出其特征,因此通过文中的粗糙集属性依赖度强化,挖掘交互式大数据特征,具体流程如图2所示.

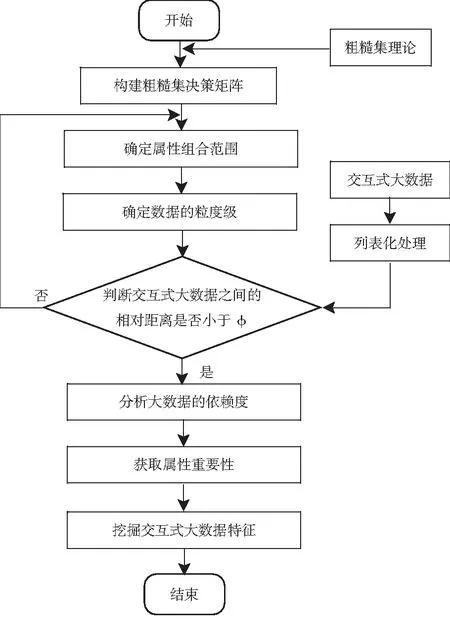
图2 交互式大数据挖掘流程

图2中通过引入粗糙集理论对交互式大数据进行列表化处理,基于交互式大数据的属性重要性,挖掘出交互式大数据的特征,利用文中方法对挖掘出的特征进行分类.

2.4 结果分析

根据图2流程挖掘出来的大数据特征,对其进行分类.利用AUC值和加速比指标衡量交互式大数据特征的分类性能.AUC值描述的是大数据特征分类方法的真实性,通常在0.5～1之间,AUC值越高,应用价值越高.加速比是衡量大数据特征分类效率的指标,可以通过下式计算,即

其中Tc为大数据特征串行分类时间,Tv为大数据特征并行分类时间.

为了验证文中方法的优越性,引入基于邻域搜索的分类方法和基于遗传算法优化的分类方法做对比,得到了如图3所示的AUC值(ROC曲线下与坐标轴围成的面积,Area Under Curve)测试结果.

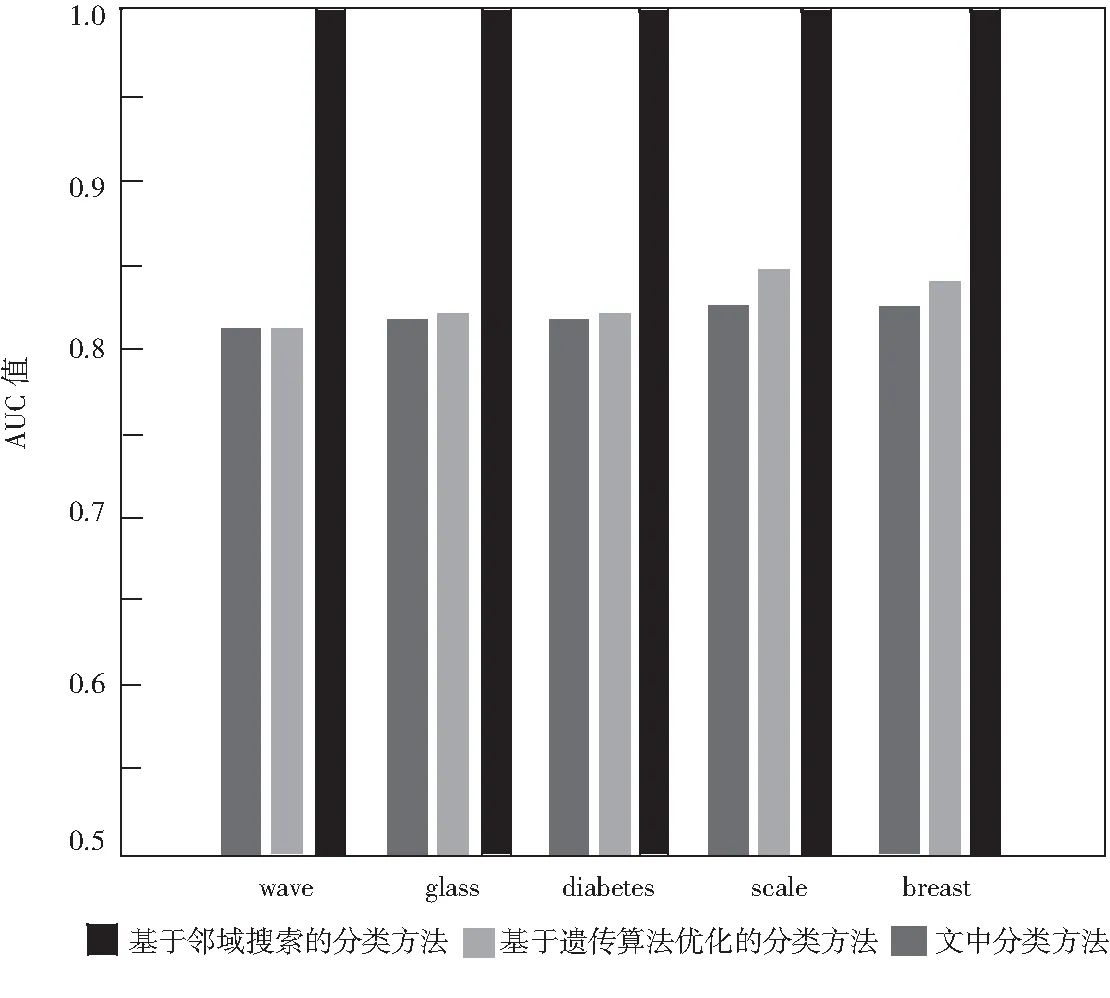
图3 AUC值测试结果

根据图3的结果可知,采用基于邻域搜索的分类方法和基于遗传算法优化的分类方法时,交互式大数据特征分类的AUC值在0.8～0.85之间,说明这两种方法在大数据特征分类中的应用价值偏低,而采用文中方法时,大数据特征分类的AUC值接近1.0,在交互式大数据特征分类中的应用价值极高.

图4 加速比测试结果

图4的结果显示,文中方法在分类交互式大数据特征时的加速比更大,5个数据集的加速比均在4.0以上,说明应用交互式大数据特征分类算法在执行数据特征分类的时间更短,提高了大数据特征的分类效率.

3 结束语

本文研究通过强化粗糙集属性依赖度,提出了一种交互式大数据特征分类方法,经实验测试发现,该方法在分类大数据特征时,应用价值大且分类效率高.在今后的研究中,将侧重于解决交互式大数据在复杂网络中的不平衡分布问题.