Properties of Cauchy integral on the Hyperbola

WEI Yuqiu,LIU Hua

(Department of Mathematics,Tianjin University of Technology and Education,Tianjin 300222)

Abstract The properties of Cauchy integral on the Hyperbola are introduced.Firstly,the definition of the principal part and order of the sectionally holomorphic function at infinity on the complex plane opened along the Hyperbola is presented.Then the properties of the Cauchy integral at infinity and the Plemelj formula on the Hyperbolaare discussed.Finally,the Hölder continuity of the Cauchy integral with principal value is discussed.

Key words Hyperbola;Generalized principal part;Plemelj formula

The Cauchy-type integrals on finite curves are discussed in classical reference [1-3].In reference [4],the author generalized the concept of both the principal part of a sectionally holomorphic function at the origin and infinity onwhich is cut by the positive real axis.In this paper,we introduce the definition of the generalized principal parts and orders at the infinity of the holomorphic function onwhich is cut by the Hyperbola.Based on this,the properties of Cauchy integral on the Hyperbola are solved in detail.

1 Preliminary

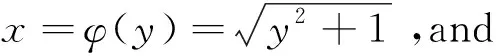
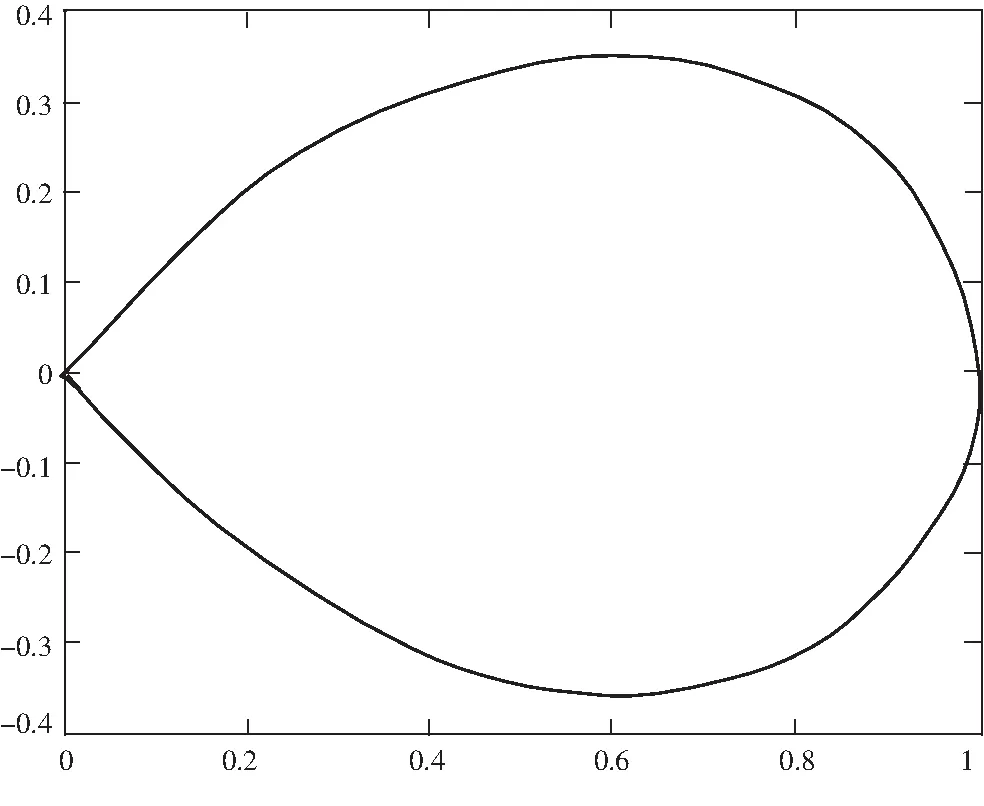
Figure 1 curve ρ(L)

Definition1[2]Assumefis defined on theL.If

whereMand 0<μ≤1are definite constants,thenfis said to satisfy Hölder condition of orderμ,denoted byf∈Hμ(L),or simplyf∈H(L).

Definition3 Iffis a function defined onL.There existst→∞such that

whereνis a real number andf*is a bounded function,or equivalently,

f(t)=O(t-ν),

(4)

then denoted byf∈Oν(∞).

If

2 Sectionally holomorphic functions jumping on the Hyperbola

In this section,we introduce the sectionally holomorphic function with the Hyperbola as the jump curve and its generalized principal parts at ∞on the Hyperbola.IfFis holomorphic in the complex plane cut by the Hyperbola,then denoted byF∈A(L).We also introduce the Cauchy-type integral on the Hyperbola.

Definition4 Letfbe a locally integrable function onL.Then

is called the Cauchy-type integral with kernel densityfalongLif it is integrable,and the Cauchy principal value integral with kernel densityfis defined by

wheret=φ(a)+ia∈L,if the integral exists.

Remark1 Obviously,for each pointlaonL,the above integral can be regarded as the sum of the following two integrals,

and

and

Lemma1[4](Analytical Properties of Cauchy-Type Integrals) Iff∈Oν(∞)(ν>0)and locally integrable onL.Then

C[f]∈A(L).

(11)

ProofBy (9) and reference[2-4],it is obvious thatC[f]∈A(L).

By the same argument,we obtain the following corollary.

Corollary1 Letf∈Oν(∞)(ν>0)and local integrable onL.Then

Definition5 LetF∈A(L).If there exists an entire functionE(z)such that

and thenE(z)is called the generalized principal part ofF(z)at ∞,denoted byG.P[F,∞].

Remark3 IfFis analytic near ∞,then it has the Laurent series

and its classical principal part is

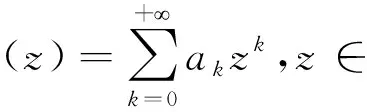
Then we have

G.P[F,∞]=P.P[F,∞],

since the entire functionG.P[F,∞]-P.P[F,∞]vanishes at ∞.

Definition6 AssumeF∈A(L).If

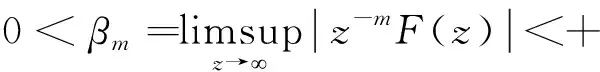
and thenFis said to be of ordermat ∞,denoted byOrd(F,∞)=m.

Remark5 Obviously,ifG.P[z-mF,∞]=βm≠0,ThenOrd(F,∞)=m.Especially,whenG.P(F,∞)is a polynomial of degreem,we haveOrd(F,∞)=m.

Remark6 LetOrd(F,∞)≤m.ThenG.P[z-m-1F,∞]=0,and we have

{F,|F(z)|=O(zm),z→∞}⊆{F,Ord(F,∞)≤m}⊆{F,G.P[z-m-1F,∞]=0}.

Theorem1 (Generalized principal part of a Cauchy-type integral at infinity) Iff∈H(L)∩Oν(∞)(ν>0)is locally integrable onL.Then

G.P[C[f],∞]=0,

whereC[f]is the Cauchy type integral given in (5).

ProofLetz=x+iy∈L.Without loss of generality,we may assumey>0.

First,we have

(13)

Case one,x≤3y.

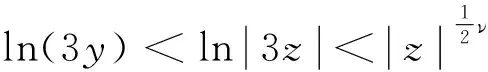
As the same as the above deduction,we have

ForI2,we have

≜I21+I22+I23+I24.

and

and

and

Here we take |z|>Δ1,Thus by (17) - (18) we obtain

Now by (14),(15) and (21) we obtain,for |z|>Δ1,

Case two.|x|>3y,

Take |z|>4,then forτ=lδ∈L,we have

Now by (22) and (23) we obtain,forzlarge enough,

which means thatG.P[f,∞]=0.

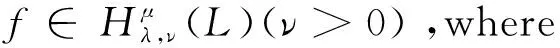
By

and Theorem 1 we obtain (24).

(25)

ProofSinceLis a Lyapunov curve,both Cauchy-type integral and singular integral onLare equivalent to the corresponding operator onρ(L),respectively.Then by (9),(10) and the Plemelj formula on the finite curve,it is trivial to check (25).

Now we prove the following Privanov Theorem.

(26)

ProofSinceLis a Lyapunov curve and according to reference[3],we can prove that (26) holds forC[f](t).By Plemelj formula (25),it also holds forC[f]±(t).