基于双矩阵博弈的群组聚合模型
李 娜,李佳美,马婧瑛
(宁夏大学 数学统计学院,宁夏 银川 750021)
对群体智能的研究起源于人们对生物界群居性生物群体的观察和研究[1].人们发现弱小个体总是通过协同工作完成捕食、迁徙和躲避天敌等工作,如鱼类群游、蚁群的聚集、兽群的围捕等.这些现象的共同特征是具有有限能力的简单个体通过信息交换和协同合作最终在集体层面上呈现出高效、强大和复杂的群体智能,从而完成复杂的任务.群体智能行为由于其在社会[2]、经济[3-4]、生物学[5]和工程学[6-8]等领域的广泛应用而得到越来越多学者的关注.
智能体群组通过协同与博弈,呈现出的群体智能行为包括一致性[5]、包围[9]、领航者涌现[10]、群体的聚合[11-13]等.聚合是微观层面常见的自然和社会现象,是指微小单元通过交互作用联结成一个更大的联合体的过程,它是一类常见的群体智能行为[11].聚合在自然界和社会中非常普遍,它是指N个粒子在一个连通图上随机游走并通过两两聚合,最终组成一个联合体的过程[12-13].文献[14]研究了社交网络上用户观点的聚合问题,作者利用非光滑分析理论证明了,只要用户的初始观点差异在一定范围内,观点最终会聚合为一个观点.然而,当个体具有自主意识,他们的交互与协调往往是一个复杂的过程.因此,文献[15]将个体间的交互建模为二人双矩阵博弈,并研究了N个个体的聚合问题.受上述参考文献的启发,本文研究存在不完全信息个体的情况下群组的聚合问题.
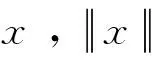
1 预备知识
1.1 双矩阵博弈
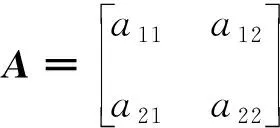
则策略对(ri*,cj*)就称为二人矩阵博弈(A,B)的纯策略纳什均衡解.而(ai*j*,bi*j*)称为纯策略纳什均衡.
在很多情况下,纯策略纳什均衡是不存在的.令Γ1={r1,r2}和Γ2={c1,c2}表示参与者P1和P2的策略空间,令α=[α1,α2]T是一个非负向量且满足α1+α2=1,其中αi表示参与者P1选择策略ri的概率.显然,α是策略空间Γ1的概率分布,即α是参与者P1的混合策略.同理,β=[β1,β2]T(β1+β2=1)被称为参与者P2的混合策略.(α,β)被称为二人双矩阵博弈(A,B)的一个混合策略.显然,在混合策略(α,β)下,参与者P1的效用的期望值为U1(α,β)=αTAβ.因此,将U1(α,β)称为参与者P1在混合策略(α,β)下的效用.类似的,称U2(α,β)=αTBβ是参与者P2在混合策略(α,β)下的效用.二人矩阵博弈(A,B)的混合策略纳什均衡可定义如下.
定义1[16]双矩阵博弈(A,B)的一个混合策略对(α,β):如果对任意混合策略(α,β)满足
(α*)TAβ*≥αTAβ*,
(α*)TBβ*≥(α*)TBβ.
则称(α*,β*)为博弈(A,B)的混合策略纳什均衡.
1.2 问题提出
对于一个由N个个体1,2,…,N组成的群组IN,设个体i在时刻k的状态记为xi(k)(k=0,1,….),xi(k)∈Rm.
假设1个体在0时刻,具有各不相同的初始状态,即xi(0)≠xj(0)对任意i≠j成立.
对于群组IN,分别给出两个个体的聚合和群组聚合的定义.
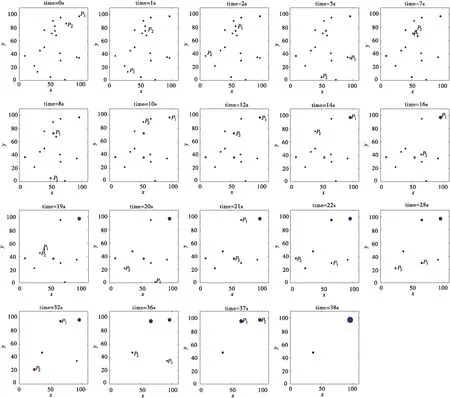
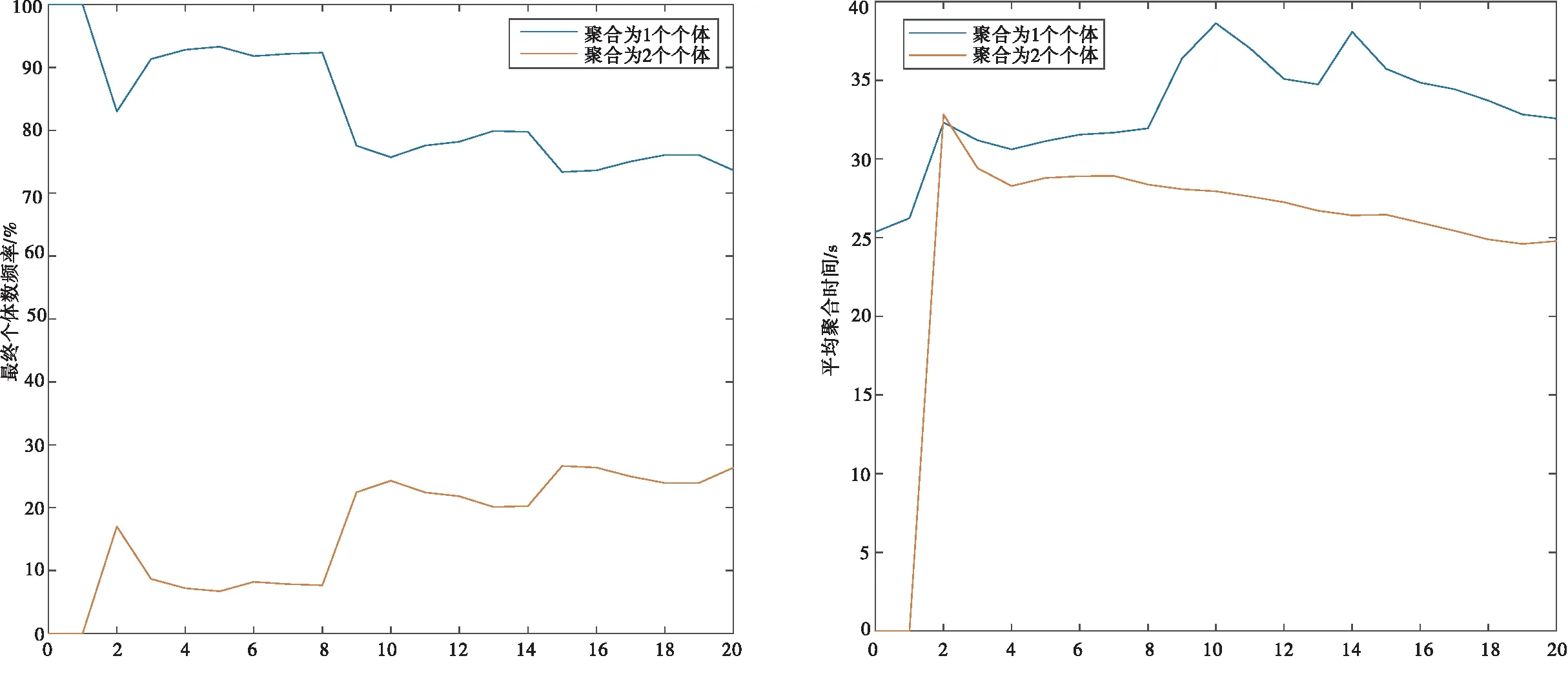
定义2(两个个体的聚合)对于群组IN中的个体i和j(i 根据定义2,当两个个体在某时刻状态相等时,它们将聚合为一个个体,此时群组中的个体数量减少1个.令nk表示k时刻群组IN中个体数量.容易得到,当nk=1时,该群组完成聚合. 定义3(群组聚合)对于群组IN,如果存在一个时刻K0,使得从K0时刻起,nk=1,(k≥K0)即个体1,2,…,N聚合为一个联合体,则称该群组完成聚合,并称K0为聚合时间. 为了使群组完成聚合,文献[15]将个体交互过程建模为如下的双矩阵博弈. 定义4[15]二人博弈G的参与者为两个个体,记为i和j.i和j博弈前的状态分别为xi(k)和xj(k),i和j通过博弈,决定其状态更新策略,更新后的状态分别为xi(k+1)和xj(k+1).每个参与者有两个备选策略,分别为合作(C)和背叛(D).如果参与者选择合作(C),则他将会改变自己的状态以完成聚合.如果参与者选择背叛(D),则无论是否能完成聚合,他都不会改变自己的状态.假设两个参与者独立地、同时做出决策.则参与者的策略对有下列四种. (i)(C,C),i,j都选择合作,改变其状态,则更新规则为 (ii)(C,D),i选择合作,改变其状态,j选择背叛,不改变其状态,则更新规则为 xi(k+1)=xj(k+1)=xj(k). (2) (iii)(D,C),i选择背叛,不改变其状态,j选择合作,改变其状态,则更新规则为 xi(k+1)=xj(k+1)=xi(k). (3) (iv)(D,D),i,j都选择背叛,保持状态不变,则无法聚合,更新规则为 对于参与者i和j来说,博弈的效用可分解为如下两个部分. (i)如果xi(k+1)=xj(k+1),i和j完成聚合,则得到奖励R. 表1 博弈G的策略对、状态更新规则和效用 由于f(·)是严格单调递增函数,如果存在ξ0>0,使得f(ξ0)=R,则当ξ(k)>ξ0时,f(ξ(k))>R.从表1不难得到,当f(ξ(k))>R时,博弈G具有唯一的纯纳什均衡策略对(D,D), 即两个参与者都会选择策略D.此时,参与者保持原有状态不变,从而无法完成两个个体的聚合.当f(ξ(k)) 定理1[15]如果f(ξ(k)) 和 选择策略C和策略D.参与者将以概率1-PD2聚合为一个新个体. 假设2f(ξmax(0)) 文献[15]中参与者选择方式并没有考虑个体被选择的概率分布模型.借鉴文献[16]的Gossip算法中交互对象选择模型,将文献[15]中的参与者选择过程改进如下. 步骤2参与者i从群组IN中选择博弈对象j; 步骤3个体i和个体j进行博弈G,若发生聚合,则聚合为一个个体.若没有发生聚合,则聚合失败. 此外,文献[15]假设所有的个体都能够获得有关博弈G的全部信息,即假设个体为完全信息个体.然而现实中,个体并不一定能够获得全部信息.因此,考虑将群组中的个体按照是否能够获得博弈G的全部信息分为完全信息个体和不完全信息个体.因此,分别研究群组中包含不完全信息个体和不包含不完全信息个体的聚合问题. 令pk表示k时刻博弈G的两个参与者聚合为一个个体的概率,即 pk=P(xi(k+1)=xj(k+1)). 由定理1可知,如果参与者可以获得博弈所需的全部信息,即对手的状态变量、博弈的效用等,那么参与者将会依据纳什均衡做出决策,即当f(ξ(k)) 完全信息的参与者会根据博弈规则做出使其效用最大化的决策.因此,在k时刻,当参与者i被选定后,它将依据期望效用最大化原则选择对手j. 定理2如果所有个体是完全信息个体,当i被首先选中作为参与者,i会选择与其距离最近的个体为对手,即 证明由假设2可知参与者i和对手会根据(5)式和(6)式确定其混合策略,从而个体i的期望效用为ξ(k)的函数 由假设2知,R-f(ξ(k))>0.容易得到, 定理3[15]如果假设2成立,且存在常数0 定理4如果假设2成立,则群组IN将以概率1聚合为一个个体,并且群组IN的聚合状态xc一定落入群组IN的初始状态围成的凸包内,即 P(xc∈conv{x1(0),x2(0),…,xN(0)})=1. 证明当假设2成立时,存在常数0 xi(k+1)=axi(k)+(1-a)xj(k),xj(k+1)=bxi(k)+(1-b)xj(k), 其中 因此,无论博弈双方如何选择策略,都有a∈[0,1],b∈[0,1].从而 xi(k+1)∈Sk,xj(k+1)∈Sk, (7) 其中 Sk=conv{x1(k),x2(k),…,xN(k)}. 而在k时刻没有参与博弈的其他个体i′∈IN{i,j}在下一时刻的状态则满足 xi′(k+1)=xi′(k)∈Sk. (8) 因此,由(7)式和(8)式可得 Sk+1=conv{x1(k+1),x2(k+1),…,xN(k+1)}⊆Sk. P(xc∈S0)=1. 证毕. 考虑群组IN中包含M(M≤N)个不完全信息个体的聚合问题.不完全信息个体是指无法获取到其他个体的状态信息以及博弈中的参数R和函数f(·)的有关信息的个体.假设这类不完全信息个体以下面的方式选择对手和策略. 假设4一个不完全信息个体参与博弈G时,它选择策略C或D的概率相等. 此时,可以得到如下结论. 当一个完全信息个体i在k时刻被选为博弈的第一参与者时,它会按照下列方式选择对手. 定理6如果假设2成立,则存在M个不完全信息个体的群组IN聚合为一个个体的概率为1.并且,完成聚合后,群组的聚合状态xc落入由群组IN的初始状态围成的凸包内的概率亦为1. 证明从定理5可知,在存在不完全信息个体的情况下,博弈G可能出现下面三种情况. (i)两个完全信息个体参与博弈.此时按照定理1,两个个体均以(5)式和(6)式选择策略C或D.根据定理3,存在两个常数0 对一个具有20个个体的群组的演化过程进行仿真实验.这些个体的状态为R2上的点,个体i在时刻k的坐标用向量[xi(k),yi(k)]T表示,则所有个体的初始状态可用矩阵 例1图1展示了由4个完全信息个体和16个不完全信息个体组成的群组的聚合过程,其中R=8.用蓝色的点表示完全信息的个体,红色的点表示非完全信息的个体,P1和P2分别表示博弈的第一个和第二个参与者.观察图1可发现,在38次博弈中,有15次博弈双方均选择策略D,这20次博弈中,博弈的参与者没有改变状态.进一步观察会发现,经过38次博弈,群组聚合为两个个体.此时,两个个体的距离ξ(38)=77.398,相应的f(ξ(k))=8.798>R.因此,当k≥38时,每一次博弈的策略对都是(D,D),也就是说参与者在该次博弈中无法聚合为一个个体.这一结论与本文理论结果是相符合的。 图1 14个完全信息个体和16个不完全信息个体的聚合过程 例2图2展示了由4个完全信息个体和16个不完全信息个体组成的群组在不同的参数R下的仿真分析,其中R∈[7,15].对每一个R,重复进行20000次仿真实验,图2(a)展示了群组停止聚合时,每一种可能情况在20000次仿真中所占的比例与R的关系.图2(b)展示了群组平均聚合时间与R的关系. 观察图2(a)可知,当R<10.37时,群组最终将聚合为1个、2个或3个个体,并且随着R的增加,群组聚合为1个个体的比例逐渐增加;当R>10.37时,聚合为1个个体的频率为100%,即20000次仿真实验的结果全部为群组聚合为一个个体.这一现象与本文所得到的理论结果定理6是相符的. 观察图2(b)可知,随着R的增加,群组完成聚合所需的平均时间逐渐减小,并且随着R的增大,完成聚合的平均时间趋向于20秒.这一现象与本文所得到的理论结果定理6亦是相符的. 为了进一步验证定理6的正确性,令R=12,重复进行20000次仿真,并将最终聚合状态的分布情况展示在图3中.观察图3可以得到,所有的最终状态都在初始状态围成的多边形内,这一结果与定理6的结论也是相符的. 图2 4个完全信息个体和16个不完全信息个体情况下,最终聚合个体数和聚合时间与R的关系 图3 4个不完全信息个体和16个完全信息个体的群组聚合状态分布图(R=12) 例3令R=9,群组中完全信息个体的个数分别为M个(M=0,1,…,20),对每个M的情况重复仿真20000次,图4(a)展示了群组最终聚合的个体数在20000次仿真中所占的比例,图4(b)则展示了随着完全信息个体数量的变化,群组平均聚合时间的变化情况. 观察图4(b)可知,当完全信息个体的数量为0或1时,群组完成聚合的博弈次数是25次左右,并且随着完全信息个体数量的增加,群组完成聚合的平均时间逐渐增加.随着不完全信息个体数量的增加,群组完成聚合的平均时间逐渐减少. (a) 集合个体数量的频率与完全信息个体数的关系 (b) 平均聚合时间与完全信息个体数的关系 研究了有限个体组成的群组的聚合过程.考虑并将个体间的聚合过程建模为二人双矩阵博弈,并进一步考虑了群组中的个体均为完全信息个体的情况下的聚合问题和群组中存在不完全信息个体的情况下的聚合问题.证明了无论群组中是否存在不完全信息个体,当个体间最大初始距离小于一个给定的值时,群组完成聚合的概率为1,并且完成聚合后的状态一定位于初始状态张成的凸包内.最后,若干仿真算例验证了本文所得到的理论结果的正确性,并进一步发现群体的聚合时间将随着不完全信息个体数和R的增大而减少.未来的研究将集中在进一步分析聚合时间与不完全信息个体数量之间的定量关系.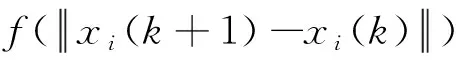
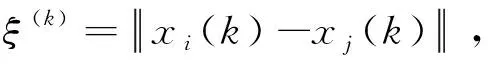

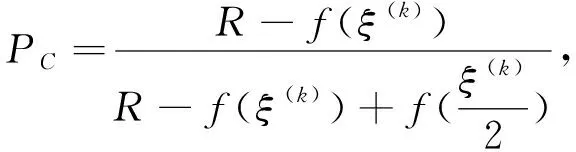
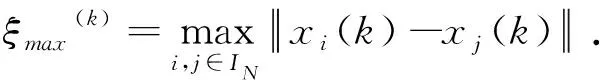

2 完全信息个体情况下的聚合问题
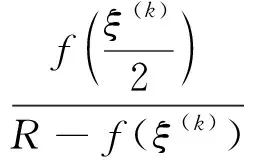
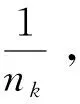
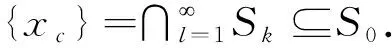
3 不完全信息个体情况下的聚合问题
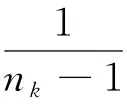
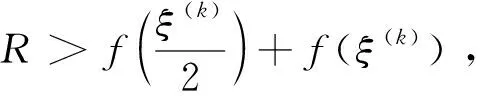
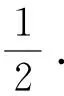



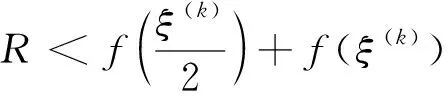
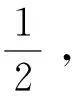
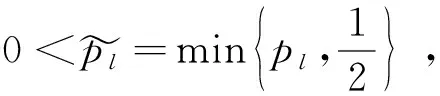
4 群组仿真实验

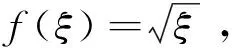



5 总结

