三维点云驱动关节目标定位和运动逆向分解算法研究

吴亚纬 郝泳涛

关键词：三维点云；机械臂；逆运动学；目标定位

0 引言

点云数据[1]是指在一个三维坐标系统里的一组向量的集合。三维点云是一种很重要的安慰数据结构，随着计算机和机器人学科的发展，三维点云也在机械臂领域获得了深入应用。

由于三维点云包含的多种信息，比如颜色、其强度等信息使得它对三维空间内的物体描述更加精准。

机械臂通常有多个自由度，这就使得机械臂拥有很高的灵活度，可以胜任很多复杂的工作，但是机械臂对环境的适应性是远不如人类的，为了提高机械臂对环境的适应能力，就需要结合计算机视觉的能力，通过三维点云提供的目标位置，机械臂通过逆向运动分解，使得机械臂运动到固定位置。

点云数据由于数据庞大，因此可以描绘出物体的三维轮廓[2-3]。在工业界，利用激光雷达获取点云数据，很早就有应用了，比如进行测高、遥感等，近几年的大规模发展得益于自动驾驶和机器人领域的火热，激光雷达成为重要的感知手段而得到人们关注，点云处理也成为热门。

点云的发展[4-8]主要是几个方面，首先从数据采集设备来说，目前包括了有人/无人机、地面、车载、便携式等多个平台共存。其次点云的场景特点有数据量大、冗余度高的特点。因此，必须在点云的数据模型、处理模型方面有一些突破，实现在点云场景方面的智能化。

与此同时，对机械臂的逆运动学求解通常有两种方法：解析法和数值法。解析法的特点包括运算速度快，但是通用性差，可以分为代数法和几何法求解，对解析法来说，串联机械臂有逆运动学解析解的充分条件是满足Pieper准则。即如果机器人满足两个充分条件中的一个，就可以得到封闭解：1） 三个相邻关节轴相交于一个点；2） 三个相邻关节轴相互平行。数值法的通用性较高，除了一些特殊的机械臂构型外，机械臂逆运动学问题很难用解析解求解，所以在很多情况下会使用数值解求解。通常设定一个目标函数，是把逆解求解问题转化为一个优化问题求数值解。

1 三维点云数据处理

1.1 PCL 库

PCL是在吸收了大量前人对点云研究的基础上，建立的大型跨平台开源库，实现了大量点云相关的通用算法和高效的数据结构，涉及点云获取、滤波、分割、配准、检索、特征提取、识别、追踪、曲面重建、可视化等。支持多种操作系统平台，可在Windows、Linux、Android、MacOSX、部分嵌入式实时系统上运行。如果说OpenCV是2D信息获取与处理的结晶，那么PCL就在3D信息获取与处理上具有同等地位，PCL是BSD 授权方式，可以免费进行商业和学术应用。

1.2 点云关键点提取

点云的关键点是一个点云数据中心有特殊特征的结合，并且其数量会远远小于初始的点云数量，可以很好地描述点云的特征。比较通用的关键点提取的算法有Harris算法、SIFT算法和ISS算法等。本文使用的是SIFT算法。

1.3 点云标准化协方差矩阵

协方差可以衡量两个随机变量在一个总体中共同变化的程度。在面临大量的数据时，或者维度很多的数据时，可以使用协方差矩阵描述不同维度的关系并且使用每两个随机变量之间的关系来描述整体维度中的关系。

计算协方差矩阵：在PCL中，首先加载需要读取的点云文件，使用Maxtrix3f创建协方差矩阵存储对象，并且创造点云质心对象用于计算协方差矩阵，最后计算点云质心，使用PCL库中现有的函数计算点云协方差矩阵。

标准化协方差矩阵：将协方差矩阵的每一个元素除以点的个数就可以得到标准化以后的协方差矩阵。

计算获得的协方差矩阵和标准化协方差矩阵用于为机械臂的定位以及运动提供相应的信息。

1.4 点云处理流程

2 机械臂建立及其运动分析

2.1 机械臂建立

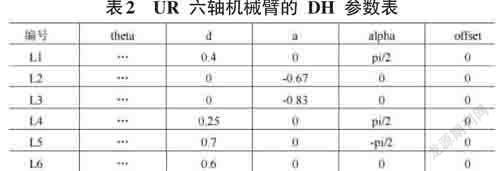
建立机械臂时通常会使用到DH参数法，这是一种1955年提出的对机械臂建模行之有效的建模方法。

机械臂运动需要一个基本的坐标系，当建立好一个DH坐标系以后，就可以根据DH参数表来计算机械臂各个关节之间的关系。

可以通过表1来建立一个标准型DH参数表，并验证机械臂的建模是否成功。

2.2 目标定位算法的研究

2.2.1 质心定位算法的研究

质心定位算法是一种比较简单的、理想化的定位算法[9]，首先需要找到未知节点的信息，这些所有的节点构成一个多边形，假设未知节点的分布相对整个节点来说是均匀的，然后通过数学方法，去计算这个多边形的质心节点。将多边形的所有顶点建立一个平面坐标系，将所有的横坐标相加后求得平均值，将纵坐标也进行相同的处理，由此求得多边形的中心作为最终结果。

可知，如果通过求多边形的中心位置来定位位置节点的位置，对于节点的连通性要求很高，当不同的节点所构成图形的中心并不与未知节点接近，这种方法的效果会很差，所以我们需要考虑一种改进的算法来应对这些弊端。

通过对质心算法进行加权，计算节点和未知的节点之间的距离，然后以每个点为圆心做一个圆，多个圆形相交所组成的区域构成一个新的多边形，然后计算这个新的多边形的中心就可以求得未知节点。

2.2.2 最小二乘法定位算法

對于最小二乘法来说，它也被叫作最小平方法。最小二乘法定位算法的目标之一是最小化误差的平方，对于多个数据建立多个方程，把多个方程的误差最小化，从而获得最优的估算坐标。

对于n个二维数据来说，我们使用最小二乘法，首先将所有的横纵坐标分别相加并求得平均值，然后计算灭个数据点的横坐标的平方并进行求和，算法横纵坐标相乘的结果并且进行求和，然后计算所要求的直线的斜率得到相应的直线方程，任取两个原来有数据中相隔较远的点的横坐标，带入求得的方程得到相应的纵坐标，得到两个点，然后用它们做回归直线，也可以拓展到三维空间中。

3 实验结果与分析

3.1 机械臂轨迹规划

机械臂要在空间中实现自由运动[10-12]，就需要在空间的坐标系的运动路径进行规划，计算出路径点，从而保证机械臂运动过程中经过这些路径点，常见的轨迹规划就包括直线和圆形轨迹。

直线规划的基本原理：当知道机器人手臂末端的起始和结束坐标时，使用三维空间的勾股定理计算两点之间的距离，即直线规划中所需直线的移动长度。我们设定运动速度，计算移动这个距离所需的时间，设定插值周期，运动时间除以插值周期得到插值步数n，从直线除以n个均匀分布的坐标。然后通过逆分解的原理，获取机械臂的所有关节信息，控制机械臂实现轨迹运动。

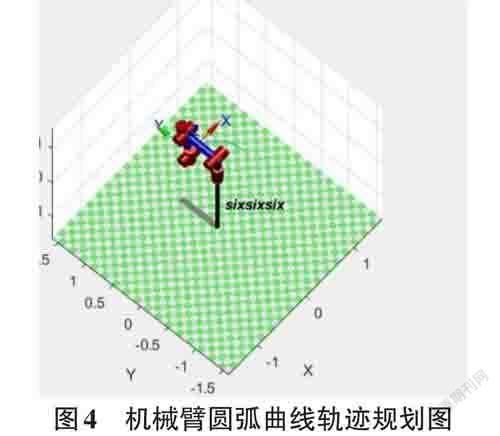
曲线规划的基本原则：当知道机器人末端的开始和结束坐标时，应该有所不同。坐标系下的空间转换、状态转移矩阵设置、将空间圆弧映射到平面空间进行处理、转换完成。然后以圆弧角度为研究对象，计算机器人运动的插值步数。线束段固定圆弧角度位移。计算与每个步骤相对应的圆弧上的点位置。这些运算求得了在空间转换以后插补点的位置坐标。最后，通过状态变换矩阵获取并发送原始空间下插值点的位置坐标。完成机械臂的圆弧轨迹规划。

3.2 机械臂运动逆向分解

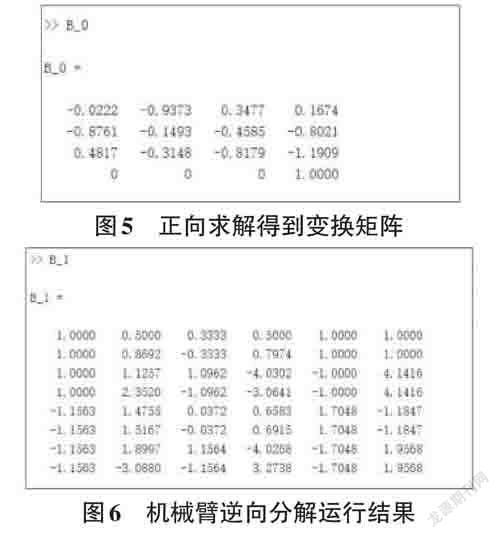
使用UR的机械臂，已知一个机械臂的变换矩阵，参照给出的DH的参数表来逆向求解出六个关节角度，并且进行验证。

使用数学解析法求得上述的关节角度，为了验证是否正确，还需要编写正向运动代码进行验证。

使用正向运动代码验证上述信息是否正确，将上述信息一个个代入编写的正向运动函数进行验证，结果均等于所求的变换矩阵，可以证明结果正确。

4 结束語

激光雷达等扫描设备带来了大量的三维点云数据，点云数据有很好的优势，对于三维点云的研究也越来越多，三维点云的出现拓展了机械臂的研究可能性。

本文介绍了处理点云的常用库PCL，并且通过PCL库实现了三维点云的读取、显示，将点云进行处理以后，计算相应的协方差矩阵和标准协方差矩阵，用于后续的机械臂研究。

本文也介绍了常用的机械臂建模方法，DH方法，并应用此方法进行了机械臂建模。我们对机械臂的直线和圆弧曲线轨迹规划的实验，并且通过PCL读取点云信息处理后得到相关矩阵变量，使得机械臂确认姿态信息，然后进行逆向分解运算。

关于点云与机械臂的结合研究还有许多东西值得学习，是十分值得探究的方向。