基于CEEMD-IBA-LSSVM的微电网短期负荷预测研究与应用

李晓辉，佟 鑫，曹敬立，李 蒙，张迎春，王梓舟

(国网冀北承德供电公司，河北 承德 067000)

0 引言

微电网是由负荷、储能及分布式电源等构成的可控供能系统[1]，其作为现代化电力系统重要发展分支之一，在促进智能电网快速发展的同时也遭遇到新的挑战[2]。微电网负荷预测结果的精准度及时效性对微电网运行稳定性、可靠性及安全性造成一定程度影响。因此，精准快速的微电网负荷预测对运行调度计划的合理制定起到积极作用，有利于微电网与大电网高效、可靠、稳定、安全运行[3-5]。针对负荷短期预测国内外学者开展了大量的研究，其中微电网负荷短期预测方法主要包含统计学模型预测、组合模型预测、机器学习预测及数据驱动预测四类。文献[6]分析光伏系统负荷受人口和经济的影响，并通过线性回归的方法对光伏负荷进行预测，最后验证回归预测模型的有效性。文献[7]将5个气象因素引入传统卡尔曼滤波模型当中形成自适应卡尔曼滤波预测模型，在一定程度上提升短期负荷预测精度。文献[8]在网络损失函数中引入一种新度量，提出一种基于全新鲁棒损失的人工神经网络(ANNs，artificial neural networks)负荷预测方法，并且通过验证得到该方法在收敛速度及预测精度方面具有一定的优势。文献[9]将改进果蝇优化算法(IFOA，improvement fruit fly optimizationalgorithm)与广义回归神经网络(GRNN，generalized regression neural network)进行融合，提出一种IFOA-GRNN负荷预测模型，并通过实例分析验证模型的有效性。文献[10]提出一种基于变分模态分解(VMD，variational mode decomposition)与蝙蝠算法(BA，bat algorithm)优化最小二乘支持向量机(LSSVM，least squares support vector machine)的短期负荷预测模型，充分考虑复杂环境因素，有效提升预测的精准度。文献[11]在最小二乘支持向量机中引入即时学习算法形成新的短期负荷预测模型，通过验证，该算法能够在保障预测精度的同时缩短整体预测时间。文献[12]对不同外部敏感因素进行充分考虑，提出基于经验模态分解(EDM，empirical mode decomposition)和特征相关性分析相结合的短期负荷预测方法，该方法减少预测模型特征数量的输入，在一定程度上提升负荷预测的精度和效率。文献[13]建立以长短期记忆(LSTM，long short-term memory)神经网络为核心的微电网负荷预测面模型，并通过实验仿真验证该模型的具有一定的优越性。文献[14]提出一种基于RNA遗传算法和布谷鸟算法的混合算法优化的风光发电预测模型，该模型兼顾布谷鸟算法与遗传算法的优点，更好的权衡局部与全局搜索能力。文献[15]构建了基于互补集成经验模态分解(CEEMD，complementary ensemble empirical mode decomposition)和区域划分自适应变异粒子群(RSVPSO，regional-division self-adapting variation particle swarm optimization)优化极限学习机(KELM，kernel extreme learning machine)的微网负荷预测模型，并通过实例验证模型的有效性。文献[16]提出一种基于经验模态分解(EMD，empirical mode decomposition)-卷积神经网络(CNN，convolutional neural network)-长短期记忆网络(LSTM，long short-term memory network)的混合电力短期负荷预测方法，通过实例仿真表明该模型能够有效缩短预测时间，提升预测精度。

综上所述，现阶段已经研究出多种微电网负荷短期预测模型，最大程度挖掘负荷序列特征，提升预测效率及精度是目前研究的重点方向。基于此，为进一步提升微电网负荷预测精度本文提出一种基于CEEMD和改进蝙蝠算法(IBA，improvement bat algorithm)优化LSSVM混合的微电网短期负荷预测模型，实现微电网短期负荷精准快速预测，合理对资源进行运行调度，实现资源的最大化利用，提升微电网经济性与可靠性。

1 互补集成经验模态分解

黄锷等人在1998年提出一种自适应时频信号处理方法，即经验模态分解(EDM，empirical mode decomposition)[17]，因其在非线性与非平稳信号处理方面的具有显著优势得到广泛的应用。EMD能够将复杂信号分解成有限数量的残余分量与本证模态函数(IMF，intrinsic mode function)，各个IMF分量能够对不同时间尺度下的原始信号特征进行呈现，但是通过这样的方法所取得的IMF分量会发生模态混叠的现象，对分解结果的准确性造成一定程度影响。随后，黄锷等人为了进一步对模态混叠现象进行改善，利用白噪声特性提出集合经验模态分解(EEMD，ensemble empirical mode decomposition)[18]，该方法能够对模态混叠现象进行有效抑制，但是信号重构之后会存在噪声残留。为了对上述问题进行解决，互补集成经验模态分解(CEEMD，complementary ensemble empirical mode decomposition)应运而生，其在EEMD的基础上进行一定的改进，引入相互独立同分布、完美负相关的互补噪声，在较大程度上消除信号重构过程中的冗余噪声，提升计算效率。

CEEMD具体信号分解过程为：

1)将一组正负成对型式的辅助白噪音ω(t)加入原始信号x(t)，得到一组新信号：

xn(t)=x(t)+εkωi(t)

(1)

式中,ωi(t)表示引入原信号的高斯白噪声，该噪声同时具备单位方差与零均值；εk表示各次选取白噪声的占比。

2)对加入白噪声的原始信号进行重复分解，对重复分解I次后所形成的IMF分量集成进行取平均操作，从而形成新的IMF分量，具体为：

(2)

式中,Ej表示EMD分解过程中获取的第j个本征模态函数。

3)一阶残差函数r1(t)的表达式为：

r1(t)=x(t)-IMF1(t)

(3)

4)r1(t)+ε1E1(ωi(t))，i=1,2,3，…，n通过EMD进行分解，当满足IMF1时，总体平均值IMF2的表达式为：

(4)

5)此时，k阶残差rk(t)的表达式为：

rk(t)=rk-1(t)-IMFk(t)

(5)

6)将r1(t)+ε1E1(ωi(t))，i=1,2,3,…，n利用步骤4)进行EMD分解，将获取的的首个本征模态函数当成CEEMD分解的IMFk+1，其表达式为：

(6)

7)重复上述步骤5)，当残差的极值不大于2时，表明残差已无法再被分解，此时获得最终残差R，其表达式为：

(7)

(8)

由式(8)可知，残差R与分解之后的IMF分量能够有效叠加重构出原始信号。

2 最小二乘支持向量机

LSSVM是在SVM算法的基础之上扩展而来，随着其在预测领域的不断应用，已经成为一种成熟的机器学习预测方法。LSSVM将SVM中不等式约束条件用等式替代，并且选用最小二乘损失函数来作为损失函数，整体结构具有样本小和风险小的特点，在很大程度上降低计算的复杂度。

LSSVM的具体回归过程为：

1)给定一样本集合{(xi,yi),i=1,2,…,N}，集合中样本输入为xi∈Rm；相对应的输出为yi∈R。原始样本通过函数φ(x)映射至高维特征空间，此时最优线性回归的函数表达式为：

f(x)=ωTφ(x)+b

(9)

式中,b∈R代表偏差；ω表示特征空间当中权系数向量。

2)基于结构风险最小原则，式(9)当中对应的LSSVM优化问题J的表达式为：

s.t.yi=ωTφ(xi)+b+ei

(10)

式中,ξ表示惩罚系数，且ξ>0；ei∈R表示误差变量。

3)对上述优化问题进行求解，首建立拉格朗日函数，具体函数式为：

(11)

式中,αi表示拉格朗日函数的乘法算子。

4)根据卡罗需-库恩-塔克条件对式(11)求解得到α与b，并且得到回归函数的表达式为：

(12)

式中,K(xi,xj)表示核函数，常见的核函数主要有径向基核函数与有线性核函数，两者的表达式为：

(13)

(14)

式中,σ2表示核函数的宽度。

由上述可知LSSVM模型有核函数宽度σ2与惩罚系数ξ两个待优化的参数，这两个参数的合理选取对LSSVM的泛化能力与抗干扰能力造成直接影响。本文在蝙蝠算法的基础上，对其缺陷进行改进从而得到改进蝙蝠算法，并运用改进蝙蝠算法对LSSVM的核函数宽度σ2与惩罚系数ξ进行优化。

3 蝙蝠算法及其改进

3.1 蝙蝠算法

蝙蝠算法(BA，bat algorithm)是由杨新社于2010年提出的一种全局随机搜索算法，该算法对蝙蝠通过回声定位捕捉猎物的过程的生物特征进行模拟，从而达到全局随机搜索。蝙蝠算法通常采用实数来进行编码，具有较少的相关参数，常应用于支持向量机(SVM，support vector machine)参数寻优[19]。蝙蝠算法将整个搜索空间当中的各个点看作蝙蝠个体；将蝙蝠搜索猎物与移动当成算法中的搜索与优化；蝙蝠移动过程中所处的位置的优劣看作求解目标的适应度值。

假设蝙蝠搜索空间的维度为D，每次迭代中各个蝙蝠的速度与位置的表达式为：

fi=fmin+(fmax-fmin)·β

(15)

(16)

(17)

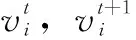
在局部搜索过程中，假如某一蝙蝠选择某一最优解，这时此蝙蝠会在该最优解附近产生新的解，其表达式为：

xnew=xold+εAt

(18)

式中,ε表示[0,1]之间的一个随机数；At表示所有蝙蝠在t时刻的响应度均值；xnew表示某最优解附近所产生的新解；xold表示当前最优解当中的某个最优解。

蝙蝠在搜寻猎物的过程当中会根据自身和猎物之间的距离对超声波的频率和响度进行实时调整，进而提升捕食效率。蝙蝠的脉冲频率及响度的表达式为：

(19)

(20)

3.2 改进蝙蝠算法

蝙蝠算法虽然具有较为简单的构造模型与优良的优化能力，但是其初始种群是通过随机方法生成，易在迭代后期出现早熟与陷入局部最优的问题，对种群多样性造成一定程度的影响。为改善蝙蝠算法所存在的问题，本文在常规蝙蝠算法的基础上，引入拉格朗日差值法、动态自适应惯性及反向学习来对其进行改进，使局部探索和全局搜索能力得到一定程度平衡，提升种群的多样性与算法性能，规避局部最优现象发生[20]。改进蝙蝠算法(IBA，improvement bat algorithm)优化LSSVM的流程如图1所示。

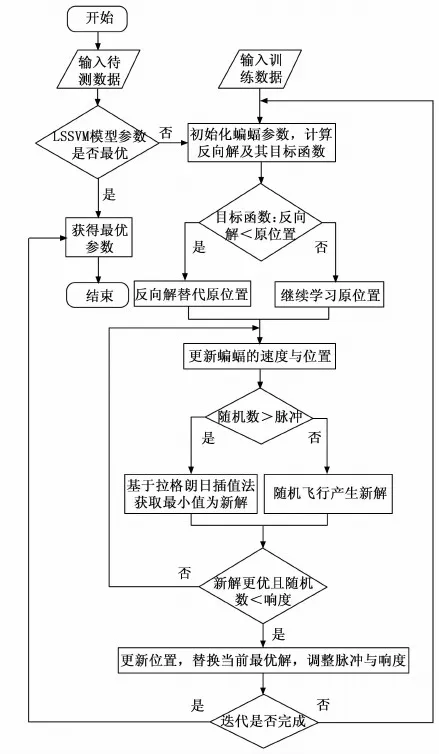
图1 IBA优化LSSVM流程图

3.2.1 反向学习

方向学习中将反向解来与原始解进行对应，基于不同方向来进行探索，其定义为：

假设P(x1,x2,…，xn)为n维空间当中的一点，并且xi∈[ai,bi]，此时xi反向解的表达式为：

(21)

在蝙蝠算法当中引入反向学习，将P(x1,x2,…，xn)当作蝙蝠算法中蝙蝠的位置，对比方反向解目标函数与原蝙蝠的位置，如果原蝙蝠位置劣于反向解目标函数，这时原蝙蝠的位置由反向解的位置代替，反之，对原蝙蝠的位置继续学习。引入反向解在一定程度上提升算法种群的多样性，规避局部最优现象的发生[21]。

3.2.2 动态自适应惯性权重

因蝙蝠算法搜索速度系数保持1不变，很大程度上降低个体灵活性和种群多样性，从而致使算法在局部探索和全局搜索出现不平衡。为解决该问题，引入聚焦距离，利用聚焦距离的变化率来对均衡蝙蝠的局部探索和全局搜索能力，从而达到惯性权重的自适应动态调整[22]。聚焦距离的表达式为：

(22)

(23)

(24)

式中,n表示种群的个数；D表示蝙蝠的维度数。

惯性权重的表达式为：

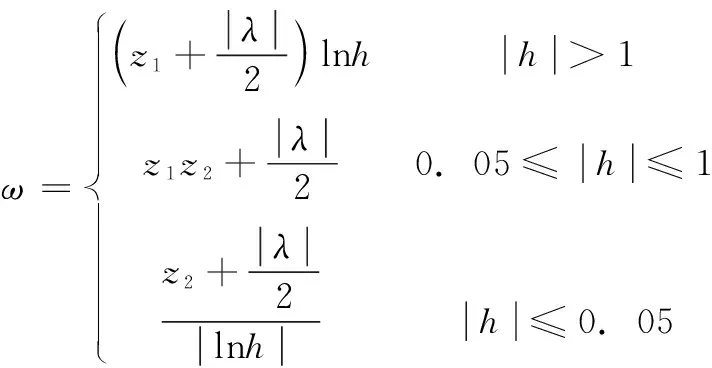
(25)

式中,z1取值0.3，z2取值0.2；λ表示[0,1]之间均匀分布的随机数。

由式(25)可知，蝙蝠在聚焦变化率处于较高水平时，呈现出较差的全局搜索能力，此时提升惯性权重，蝙蝠能够以较快的飞行速度寻找到全局最优解的范围，在一定程度上提升蝙蝠的全局搜索能力[24]；反之，蝙蝠在在聚焦变化率处于较低水平时，降低惯性权重，蝙蝠飞行速度降低，在一定程度上提升蝙蝠局部搜索能力。

综上可知，在蝙蝠算法中引入动态自适应惯性权重能够对蝙蝠局部探索与全局搜索能力进行平衡，使蝙蝠种群更好适应环境，提升整体寻优效率。

3.2.3 拉格朗日插值法

为进一步提升蝙蝠算法局部搜索能力、提升收敛速度，引入拉格朗日插值法来对多项式进行模拟[23]，拉格朗日插值的表达式：

(26)

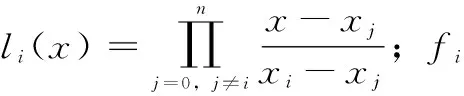
选取全局最优解gbest的j维当中的3个点进行信息生成并对其进行拉格朗日插值操作，其中一个为目前全局最优解，剩余两个为最优解附近的扰动，上述关系的表达式为：

σ=rand*η*v(i,j)

x0(j)=gbest(j)

x1(j)=gbest(j)+σ

x2(j)=gbest(j)-σ

(27)

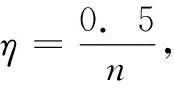
x0,x1,x2在j维空间当中能够通过拉格朗日插值生成抛物线，进而取得最小值，将当前最优解目标函数值与上述获取的最小值进行对比，进而对位置信息进行更新。拉格朗日插值的计算表达式为：

(28)

4 基于CEEMD-IBA-LSSVM混合模型微电网负荷预测模型

4.1 数据预处理

为进一步提升组合模型的训练速度，在负荷预测预测之前，需要对负荷原始数据通过式(29)进行归一化处理。

(29)

式中,p表示原始负荷值；p′表示原始负荷经过归一化后的值；pmin表示最小负荷值；pmax表示最大负荷值。

为了进一步提升预测结果的规律性与准确性，需要对微电网的硬性因素进行充分考虑，本文主要对环境温度、天气类型及日类型进行考虑。

针对日类型进行处理：休息日为0.5，工作日为1；天气类型处理：晴天为1，阴天、多云及雾天为0.5，雨天和雪天为0；应用式(30)对温度进行归一化处理。

(29)

式中,T表示原始温度；T′表示经过归一化后的温度值；Tmin表示最小温度值；Tmax表示最大温度值。

4.2 模型评价指标

本文选取均方差根误差(RMSE)、平均相对误差(MAPE)及平均绝对误差(MAE)来作为组合预测模型的评价指标，对模型进行量化评价，各评价指标的表达式为：

(30)

(31)

(32)

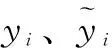
4.3 微电网负荷预测流程

因微电网在运过程中负荷会受到环境因素影响，故负荷序列会呈现出一定程度的非平稳与非线性的特征。由于CEEMD在非平稳序列处理方面具有显著的优势及LSSVM在短期负荷预测中效果显著，并运用IBA对LSSVM参数进行优化，故，提出一种CEEMD-IBA-LSSVM混合微电网负荷预测模型，该预测模型的流程如图2所示。

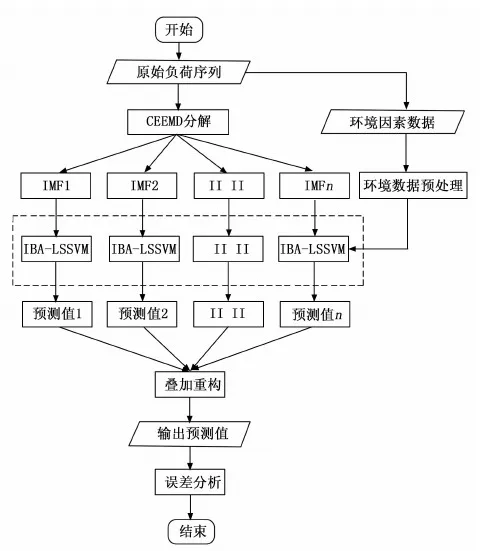
图2 CEEMD-IBA-LSSVM混合微电网负荷预测模型流程图

Step1:利用CEEMD来对微电网负荷的序列特征进行深度挖掘，从而获得多组残余分量与IMF分量；

Step2:对环境因素变量、残余分量及IMF分量数据进行归一化，并按照一定比例进行测试集与训练集划分；

Step3:将归一化数据完成的数据作为输入数据，构建IBA-LSSVM模型，对最大迭代数合种群数据等数据进行设置；

Step4:利用IBA优化LSSVM流程(图1)对核函数宽度σ2与惩罚系数ξ进行优化，最终得到最优σ2和ξ；

Step5:基于最优σ2和ξ下的LSSVM模型对测试数据进行分解预测，得到残余分量与IMF分量的结果，之后对上述结果进行叠加重构，最终获得微电网负荷预测值；

Step6:利用均方差根误差(RMSE)、平均相对误差(MAPE)及平均绝对误差(MAE)来对组合预测模型的性能进行评价。

5 仿真实验分析

5.1 数据分解

选取某微电网连续100天每小时的负荷数据作为实验数据，共计2 400组数据，将前95天2 280组数据作为训练数据，后5天120组数据作为测试集，并且这些数据样本当中包括每日天气类型、日类型及温度等因素。首先，利用CEEMD对前95天2 280组数据进行分解，并且基于频率尺度对其进行组合，最终获得残余分量与8组IMF分量；其次，通过IBA-LSSVM模型对预处理之后的环境变量数据、残余分量及IMF分量进行训练；最后，运用测试集数据对模型进行验证。

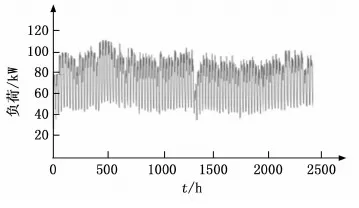
图3 微电网负荷采集数据

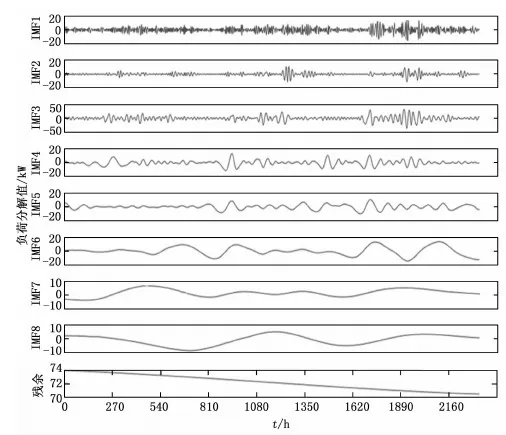
图4 CEEDM分解图

5.2 算法参数设置

IBA是一种对惯性权重、收敛速度及种群多样性进行改进的蝙蝠算法，其主要参数如表1所示。

表1 IBA算法主要参数表

由于IMF1-IMF4波动较强，则在构建预测模型时选取具备良好局部学习的基函数作为核函数，即式(14)；IMF5-IMF8及残余波动相对平缓，则在构建预测模型时选取具备良好全局学习的显函数函数作为核函数，即式(13)。IBA算法对LSSVM核函数宽度σ2与惩罚系数ξ优化得到的最优值如表2所示。

表2 LSSVM参数最优解

5.3 仿真结果及分析

为了对本文构建模型在微电网短期负荷预测领域的优越性进行验证，选取EEMD-BA-LSSVM、EEMD-IBA-LSSVM、CEEMD-BA-LSSVM及CEEMD-IBA-LSSVM四种不同预测模型对测试集120组数据进行预测，并将预测结果与十几数据以拟合曲线的形式进行呈现，具体如图5所示，4种模型3种不同评价指标如表3所示。

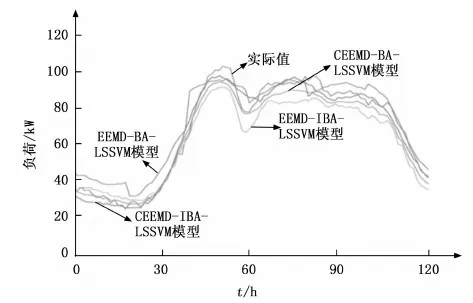
图5 负荷预测对比图

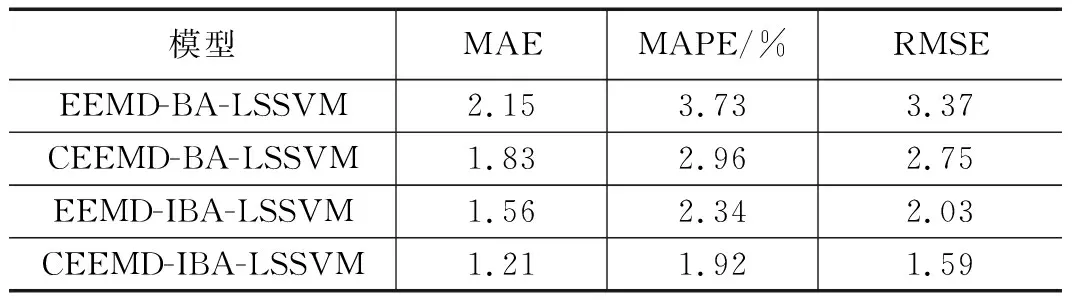
表3 4种不同预测模型指标对比表

由图5和表3可知，EEMD-BA-LSSVM、EEMD-IBA-LSSVM、CEEMD-BA-LSSVM及CEEMD-IBA-LSSVM四种不同预测模型均能够很好的对实际微网负荷曲线进行拟合，其中本文构建的CEEMD-IBA-LSSVM预测模型与实际负荷最为接近，且的均方差根误差(RMSE)、平均相对误差(MAPE)及平均绝对误差(MAE)最小，预测准确率约为98.21%，更能准确预测微网短期负荷的波动趋势，提前预知微电网短期负荷，合理对资源进行运行调度，实现资源的最大化利用，提升微电网经济性与可靠性。对于不同分解方法的预测模型，通过CEEMD分解的预测模型较相对应EEMD分解预测模型预测误差更小，更为接近实际负荷数据，这表明CEEMD在对模态混叠现象有效抑制的同时，也使EEMD 的残留噪声问题得到一定程度减弱。对于不同优化算法的预测模型，通过IBA优化算法的预测模型较BA优化算法预测模型预测误差更小，更为接近实际负荷数据，这表明IBA优化算法能够使局部探索和全局搜索能力得到一定程度平衡，提升种群的多样性与算法性能，规避局部最优与早熟现象。

6 结束语

针对微电网负荷特性，提出一种CEEMD-IBA-LSSVM混合微电网负荷预测模型，通过研究得到如下结论：

1)通过互补集成经验模态分解(CEEMD)来分解微电网负荷序列，能够使微电网负荷序列受环境因素的影响得到有效弱化，在一定程度上降低预测的复杂度，提升预测效率；

2)对蝙蝠算法(BA)进行改进，使局部探索和全局搜索能力得到一定程度平衡，提升种群的多样性与算法性能，规避局部最优与早熟现象；

3)基于改进BA对LSSVM中核函数宽度σ2与惩罚系数ξ进行优化，形成 CEEMD-IBA-LSSVM混合微电网负荷预测模型，能够提前预知微电网负荷，合理对资源进行运行调度，实现资源的最大化利用，提升微电网经济性与可靠性；

4)实验仿真表明：CEEMD-IBA-LSSVM混合微电网负荷预测模型与其他预测模型相比具有较高的运行效率与预测精度。

在今后的研究当中，需要探究更多影响微电网的因素，并构建多因素约束下的预测模型，从而提升多因素影响下的模型泛化能力与预测精度。