面向毫米波大规模极化敏感阵列的多径信号二维快速测向算法*

张喆，文方青**，师俊朋

（1.三峡大学水电工程智能视觉监测湖北省重点实验室，湖北 宜昌 443002；2.三峡大学计算机与信息学院，湖北 宜昌 443002；3.国防科技大学电子对抗学院，安徽 合肥 230037）

0 引言

未来6G 的世界是一个万物互联的世界，空天地的一体化通信让人们可以随时随地地进行便捷、安全、快速、智能的信息交互。DOA（Direction-of-Arrival，波达角）估计是通信、定位和传感的核心任务。因此，它是6G 通信网络无线通信的规范任务[1]。由于无线信道的复杂性（如反射、二次反射等），电磁波在传播途中往往会产生多径信号，即相干源。多径信号往往会造成无线信号的衰落，对其进行DOA 估计是一个重要的课题。此外，B5G/6G 中的大规模MIMO 天线阵列一般会带来巨大的计算复杂度，故高效率的天线技术也是DOA 算法研究需要突破的问题之一[2]。

2D-DOA（Two-Dimensional Direction-of-Arrival，二维波达方向）估计作为阵列信号处理领域中的重要问题之一，已经涌现出许多基于传统标量传感器进行测向的算法。针对非相关信号，Wu[3]等人提出的适用于均匀线阵的PM（Propagator Method，传播算子法），利用数据之间的线性关系进行高精度测向，但缺陷是只适用于均匀阵列。Xi[4]等人提出的适用于L 型阵列的子空间算法，通过重排特定的向量得到噪声子空间，再进行二维的搜索，导致该算法计算量较大。对于更符合实际的相干信源场景，Chen[5]等人提出了SS（Spatial Smoothing，空域平滑）算法对相关信号进行去相关，构造子矩阵并取各子矩阵的平均来恢复协方差矩阵的秩，但此方法损失了阵列的有效孔径。Kwong[6]等人提出通过协方差矩阵重构来恢复其秩，但此方案对阵列的要求必须是均匀的。刘[7]等人提出的适用于L 型阵列的二维MUSIC 算法，但此方案由于要构造Toeplitz 矩阵，并在Toeplitz 矩阵基础进行矩阵重排，最后进行二维搜索，所以计算量非常大。更值得一提的是，传统标量传感器输出只是标量，包含的信息较少，分辨率低[8]。

近年来，伴随着EMVS（Electromagnetic Vector Sensor，电磁矢量传感器）这一新型分支的兴起，基于EMVS 阵列进行信号处理得到了广泛的关注。EMVS 通过相互正交的偶极子和磁环感知来波信号，单个EMVS 不仅能感知来波的2D-DOA 信息，还能感知来波信号的极化特征。所以与传统标量传感器组成的阵列相比，EMVS 组成的阵列在理论上具有明显的优势，体现在较高分辨率、较强抗干扰、较稳定检测能力和极化多址能力这四个方面[9]，因而引起国内外学术界和工程界的广泛关注。2D-DOA和极化估计也相应成为目前电磁矢量传感器阵列研究的热点问题之一。经过近几十年的发展，已涌现大量优秀的估计算法，如2013 年Ren[10]等人提出的适用于URA的酉变换算法，及2019 年Ahmed[11]等人提出的适用于矩形阵列的PARAFAC（Parallel Factor，平行因子）算法。

已有部分研究关注EMVS 阵列中的相干信号测向问题。2004 年，徐[12]等人提出的适用于单一阵元或多阵元的空间平滑算法。2004 年，Rahamim[13]等人提出的适用于任意几何形状的PS（Polarization Smoothing，极化平滑）算法。2010 年，He[14]等人提出的适用于均匀矩形阵列的PDS（Polarization Difference Smoothing，极化差分平滑）算法。随着大规模MIMO（Multiple-in Multipleout，多输入多输出）技术的出现，利用大规模EMVS 解决DOA 估计问题成为人们新的研究热点，Wen[15]等人提出了CS（Compressive Sampling，压缩采样）框架，对数据矩阵进行降维处理后特征分解得到信号子空间，最后利用旋转不变性和归一化向量叉积技术得到2D-DOA估计。Wan[16]等人则基于四元数理论，在MUSIC 的基础上，提出一种QNC-MUSIC（Quaternion Non-Circular MUSIC，四元数非圆形MUSIC）的新算法，虽然DOA估计仍需要进行频谱搜索，但极化估计有闭式解。

本文聚焦现存算法的优点和不足，本文提出了一种改进的多径效应背景下2D-DOA 与极化参数联合估计的快速方法。本文方法通过对EMVS 阵列数据进行简单重排即可消除由于相干源引起的秩亏问题，再利用PM 算法从重排的数据中获得2D-DOA 信息，最后通过最小二乘算法获得极化特征。所提算法无须高维特征分解，且其适用于单快拍场景。相比现有算法，本文算法具有计算复杂度低、估计精度高的优势。仿真结果验证了所提算法的性能优势。

1 信号模型与问题描述

考虑图1 所示的接收阵列，该URA（Uniform Rectanglearray，均匀矩形阵列）由M×N个EMVS 组成（单个电磁矢量传感器由三个正交的电偶极子加上三个正交磁环组成[17]，本文假设它们共置于空间中一点），d表示阵元间距，λ为信号波长。假设有K个远场窄带的平面横波入射到该阵列，令θk，φk，γk，ηk分别为第k个（k=1,2,……,K）信源相对于接收阵列的俯仰角、方位角、辅助极化角和极化相位差，(θk,φk)也被称为信源的2D-DOA。接收阵列（L次采样）输出可以表示为[18]：

图1 极化URA示例

式中，uk=sinθkcosφk，vk=sinθksinφk，bk为单个EMVS输出的具体形式，其前三行元素代表入射电场的所有三个笛卡尔分量，后三行元素则表示入射磁场的所有三个笛卡尔分量。当估计2D-DOA 时，EMVS 阵列不仅可以利用入射信号的空间分集，而且可以利用它们的极化分集，因此它们可以提供比传统标量传感器阵列更精确的角度估计。

本文聚焦于多径环境中信号相干问题，由于电磁波信号的反射与折射，使入射到阵列的信源中既包括需要识别的信号本身，又包括频率相同但相位不同的多径信号，相位互相叠加使得原来的信号产生失真或者错误。更进一步地，相干信号会造成阵列输出的信号协方差矩阵秩亏，导致基于特征值分解的算法性能下降甚至失效。

2 本文算法

下面讨论如何在由EMVS 组成的URA 中利用矩阵重排的方法进行信号的解相干，并进一步利用PM 完成二维DOA 的估计。

2.1 基于矩阵重排的秩亏消除

本文首先将式(1) 中的阵列输出Y进行矢量化得到一组新的数据Z∈C6MNL×1，其具体的形式如下：

式中，Unvec6N()即把y这一包含6×M×N×L个元素的列向量从上到下取每6N个元素为一列，依次从第一列排到最后共M×L列，得到一个维度为6N×ML的矩阵。且容易得到(ST⊙Ax)T为满秩矩阵，证明如下：

令ci，cJ(i,j∈ {1,2,…,K})分别是(ST⊙Ax)中不同 的两列，即：

定义By(ST⊙Ax)T+Unvec6N(Nz)，X相应的 协方差矩阵R为：

式中，Rx是(ST⊙Ax)T的协方差矩阵，I6N为6N× 6N的单位矩阵。

2.2 2D-DOA进行估计

在本节，推导出一种基于PM 的高效2D-DOA 测向算法，它不需要进行谱峰搜索。PM 是一种基于转向矢量划分的线性算子，并且可以很容易地从数据中确定[19]。所提出的PM 算法基于以下划分：

式中，Q1由By的前K行组成，Q2由剩下的6N-K行组成。易知Q1为K×K维的范德蒙德矩阵，所以它是满秩的，即By的前K行是线性独立的，剩余的6N-K行Q2可以由这K行的线性组合表示。由此，定义一个(6N-K)×K维的矩阵为传播算子P[20]，且它满足以下关系：

进一步的，令P1，P2分别代表PH的前(6N-1)-K行与最后的(6N-1)-K行，则有以下关系[14]：

为了得到P，将R与By进行类似的划分：

同样地，R1为R的前K行，R2为R的剩余6N-K行。通过观察R=ByRxBy+σ2I6N，不难发现By中的线性关系对R也适用。即有：

此关系只适用于无限样本的情况。对于有限的采样，给出P的最小二乘估计：

式中，arg{}表示取对应的相位角。由于相对于x轴的方向余弦估计与对估计相似，这里就不再重复赘述。有了估计的和，通过Van[21]所提出的矩阵扰动法得到正确的2D-DOA 对。

最后，2D-DOA 估计即为：

3 算法分析

3.1 可辨识性

本文所提方法的可识别性受到K的最大可能值的约束，它等于无噪声X的最大秩。很明显，无噪声X的最大秩为min{6N,ML}。从式(8) 中可知，要想Q2存在，需满足K＜6N，又由(10) 中P1、P2的划分，必须满足K＜6(N-1)。因此综合上述来看，K=min{6(N-1)-1,ML}。另外，在表1 中，列出了本文所对比方法的可识别性。

表1 可识别性比较

3.2 复杂度

表2 复杂度比较

3.3 CRB

根据Wen 等人[15]，2D-DOA 的确定性CRB 由下式给出：

4 计算机仿真

本节采用蒙特卡洛方法验证所提算法的有效性。在仿真中，假设接收阵列为M行N列的均匀矩形阵列，每个阵元都是完备的共址式EMVS。阵元间距为d=0.5λ，α为相关系数。假设有K=3 个远场信号，其参数分别为θ=(40°,10°,60°)，φ=(-15°,45°,20°)，γ=(12°,39°,63°)，η=(33°,47°,-21°)。此外，假设已收集L个样本。仿真的每个图的结果都依赖于200 次独立的试验。在仿真中，信号与噪声比（SNR）被定义为，Y与N均为表达式(1)中的数据矩阵。性能评估采用RMSE（Root Mean Square Error，均方根误差）评价。值得一提的是，算法仿真对于相关信源强度的建模采用的是自回归（auto regression）过程，相关系数矩阵定义为：

式中α∈ [0,1]为相关系数。这种相关形式更接近实际的情况，实用性强。

首先，所提相干估计器的2D-DOA 估计的散点图结果由图2 给出，其中M=6，N=6，SNR=20 dB，L=1，α=1。可以清楚地看到，所有的参数都正确估计和自动配对。结果表明，本文方案可提供信源2D-DOA 估计的闭式解。

图2 所提出方法的散点结果

其次，图3 中给出了信源2D-DOA 估计在不同信噪比下 的平均RMSE 性 能，其中M=6，N=6，L=500，α=1。为了突出本发明方案的可靠性，将本方案同Spatial-Smoothing（SS）算法[12]、ESPRIT-Like（ES-like）算法[22]、Polarization-Smoothing（PS）算法[13]以及URA 的克拉美罗界（标记为CRB）进行比较。显然当信噪比逐渐变大时，所有算法都会提供更好的RMSE 性能。然而，本文所提的方法的RMSE 比所有对比的算法更低，且在低信噪比时仍有较高精度，这表明本文方案能提供更精确的估计性能。

图3 不同SNR下的估计性能

此外，图4 还给出了不同采样次数下的平均RMSE性能，其中M=6，N=6，SNR=16 dB，α=1。值得注意的是，当采样次数增加时，所有算法都会提供更好的RMSE 性能。然而，本文所提的方法的RMSE 比所有对比的算法更高，特别是在采样次数较少时（如L＜10），这表明本文方案的实用性更强。

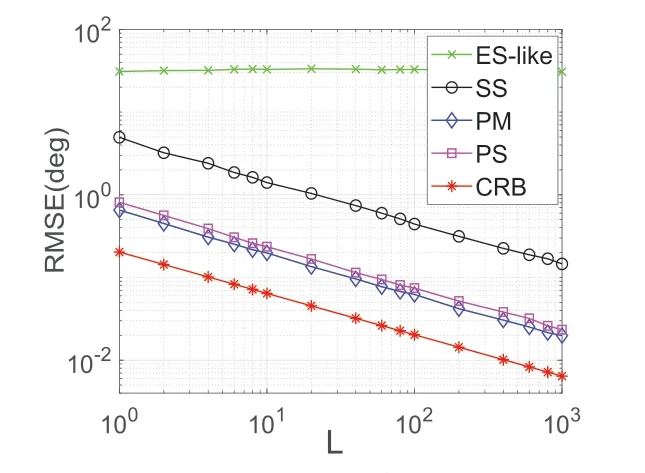
图4 不同L下的估计性能

最后，本文对比了不同相关强度下的RMSE 性能，其中M=6，N=6，L=500，SNR=5 dB。从图5 可以看出，在信号相关强度较低和较高时，即非相关信号和相干信号两种场景下时，PM 都能保持稳定的低RMSE，且在α＞0.4的条件下性能优于现有的方案。

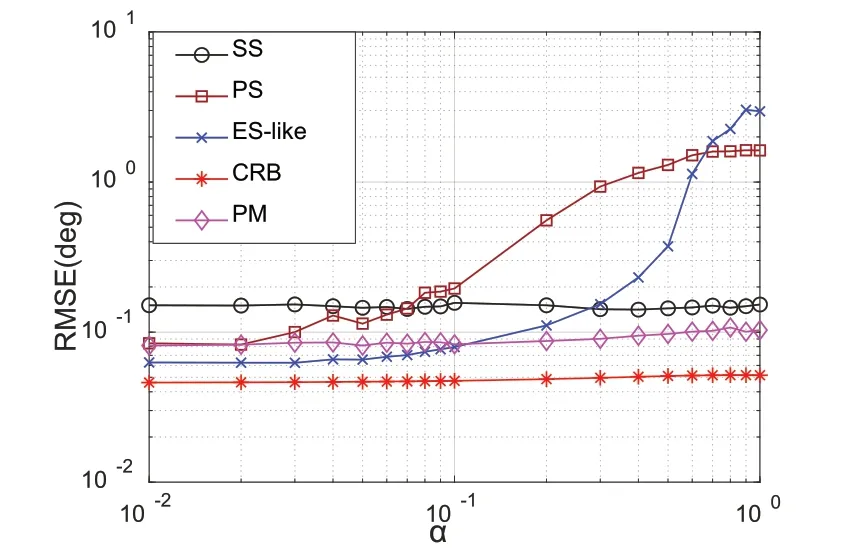
图5 不同相关强度下的估计性能

5 结束语

本文提出一种基于矩阵重排的多径背景下的2D-DOA 估计算法。不同于主流的空间平滑和极化平滑算法，矩阵重排通过将空域信息和极化域信息结合起来解决因相干信号而导致的秩亏问题，并利用线性算子得到了一种高效的2D-DOA 测向方法，相信该算法在下一代移动通信网络中利用毫米波大规模敏感阵列得到DOA估计方向上会有较大的作用。