简约而不简单
———特级教师张齐华《等值分数》课例赏析
文|严巧华
在“聚焦新课标 赋能新课堂”2022 江苏省小学数学教材研讨培训会中,学习了特级教师张齐华《等值分数》一课,让我再一次领略到了数学王子的课堂魅力。纵观整节课,给我的总体感觉是紧扣新课标,简约不简单。看似普通的教学设计,不经意间的一个追问,一个小小的动手做环节,总能调动学生的学习积极性,激起学生思维的火花。教师用学生能够理解的方式,在鲜活生动的数学课堂中,促进其理解和内化数学核心素养。
一、简约的导入设计,开放的思维引导
教学片断:
导入环节,张老师创设了一个简单的故事情境:小熊和大熊分同样大的饼,小熊平均分2 份,大熊平均分4 份,各吃其中一些,谁吃得多?
生:同样多。
师:什么情境下吃得一样多?
生:小熊吃了它2 份中的1份,大熊吃了它4 份中的2 份。
师:还有没有其他可能?
师:还有其他可能吗?
师:刚才提到了几个分数?(出示圆片图)哪两个分数相等?
【赏析:《义务教育数学课程标准(2022年版)》(以下简称“新课标”)指出,在教学中可以从学生已有的知识经验和思维水平出发,根据学生数学学习的心理特征和认知规律设计教学活动。本节课的内容是等值分数,对三年级学生而言,这个概念相对来说有点抽象,在此之前,学生可能知道这两个分数是相等的,但并不知道这就是等值分数。如何让学生突破对等值分数概念的认知,形成初步的表象,考虑到三年级学生的年龄特点,张老师设计了小熊分饼的教学环节,一句简单的“各吃其中一些,谁吃得多”,将学生的思维调动起来。
张老师设计的小熊分饼实际上是给等值分数的生成促成了一个生长点,让学生体会到等值分数与已有知识的联系。张老师在设计问题时并没有直奔主题,直指等值分数,而是用“各吃其中一些,谁吃得多”引导学生找到三种可能性。这一环节的设计,旨在引导学生学会用数学的思维去思考,用数学的语言去表达。不仅从深层次沟通了分数知识和已有知识的联系,也让学生体会到了分数的大小关系,而相等只是其中的一种。导入设计虽简约,但开放的问题将教学引向了深入,为等值分数的研究拉开了序幕。】
二、简约的操作设计,扎实的过程体验
教学片断:
小贴士:1.同桌合作,折一折、比一比、画一画,把理由说清楚;2.比一比,看哪个小组的方法多。

生2:我是算出来的,大家看,这边有4 份,这边有2 份,4÷2=2,代表这个也可以只分成两份,所以这两个也是一模一样的。
师:我听到他好像将4 份变成了2 份,这是什么意思呢?
生3:我觉得他的意思就是指可以把这一条线挡住,就能发现它也仅仅是在中间划了一刀,跟这个是完全一样的。
师:他竟然在头脑当中把中间这条线给藏了起来,现在看起来像几分之几?
师:既然可以把它的线藏起来,那么?
生:原来平均分的2 份变成了4 份,原来取的1 份变成了2 份。
师:不过刚才从左往右是分,反过来从右往左是什么?
生:合。(板书:分/合)
(学生尝试说一说)
师:相等相等,我得等于你,你也得等于我……
【赏析:汇报环节,学生呈现的做法和想法又带给我们不一样的惊喜。在这一环节中,教师紧扣两幅图片,让学生折一折、看一看、比一比、想一想,充分利用手边的素材,通过直观操作,数形结合,一方面让学生对两个分数有了更深刻的感知,另一方面,有了图片素材的支撑,让学生的思维更加具象。由比到算到分再到合,由直观到抽象,学生的思维逐步深化,循序渐进。最后引导学生用规范的数学语言去表达,让学生的思维得到进一步提升。
当一个学生提到了除法,张老师没有花费过多精力去让学生探讨除法找规律,而是不着声色的设问,借助学生的发言,适时地引导,在学生第一次接触等值分数时,让学生充分观察图形,运用几何直观,使抽象思维转化成形象思维。如果刚开始少了这样的环节,直接用除法让学生抽象出等值分数的规律,这样的学习看起来让学生走了“捷径”,但却没有让学生充分经历学习过程,学生对于等值分数的理解是不够深刻的。】
三、简约的教学延伸,无限的学习拓展
教学片断一:
生:分母每次增加2,分子增加1。
生:分子和分母不同,但分子和分母都扩大了相同的倍数。
师:分母不同,其实本质上就是分数单位不同,比如说这几个分数的分数单位是什么?
师:仔细观察这些分数单位,好像一个比一个变的?
生:小。
生:虽然分数单位越来越小,但是分数单位的个数越来越多。
师:这就是藏在等值分数背后的数学奥秘。
教学片断二:
师:马上就要下课了,有同学一定在想,学了半天的等值分数到底有什么用?让我们再一次回到课前小熊、大熊分饼的故事上来,一开始谁多?
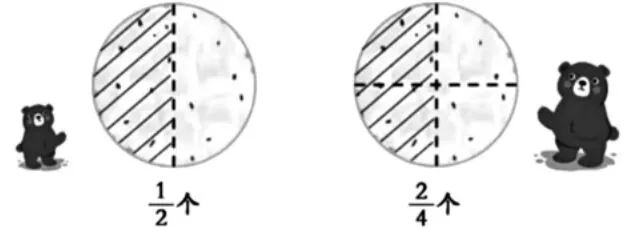
生:一样多。
师:那万一是下面的分法呢?

生:大熊多。
师:本课之前也许你觉得大熊多是看出来的,现在谁能结合等值分数说说为什么个比个多?
师:看来等值分数可以帮助我们比较分母不同的分数的大小。
【赏析:本节课的内容是等值分数,张老师的视野并没有局限在等值分数这一个点上。在片断一中,张老师拓展了分数单位,让学生把等值分数和分数单位进行了串联。新课标也强调了知识的一致性和整体性,分数单位的呈现,可以深入地帮助学生更好地理解这些分数为什么相等,分数单位在不断变小,分数单位的个数却在不断增加,这里蕴含浓浓的推理意识,在整个思考过程中,学生的数感得到了培养,也让学生从不同角度了解到等值分数,从形式到内涵拓宽了等值分数。而在片断二中,个饼大于个饼,学习本课之前,学生可能是通过直接观察或是已有的生活经验得到的,通过学习等值分数,发现原来可以变成等值分数,再用同分母的两个分数比较,进而得出结论。从最初的数学眼光进入,到中间用数学思维去思考,再到最后用数学语言去表达、应用,既用“三会”的整体框架架构了整个课堂,又将知识的延续性和一致性进行了完美的诠释。】
教学片断三:
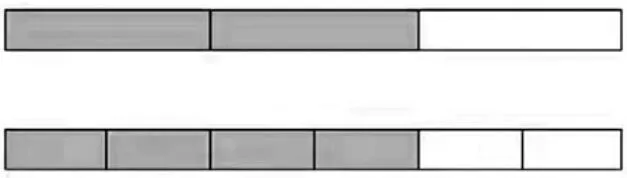
师:在这幅图里藏着两个等值分数,是多少?
师:你能说完吗?
(教师根据学生的回答逐步将分数墙补充完整,并加以呈现)
师:用尺子推一推,可以找到等值分数。移动尺子,还能找到其他等值分数吗?(教师在屏幕上演示,让学生找一找、说一说)
【赏析:在这一环节,张老师一边复习等值分数,一边根据学生的回答出示图片,最终形成了分数墙。在小学阶段,分数墙可以帮助学生进一步理解小数、分数、百分数的意义,进一步沟通各种数之间的内在联系。分数墙的作用和魅力还在于它是触发学生猜想和验证的“脚手架”,它能将复杂的数学思考变得简单。张老师充分考虑到了这一点,在三年级接触分数的初始阶段,不着痕迹的出示分数墙,在此基础上延伸教学活动,不仅使教学内容得到了充分的拓展,也让学生的思维产生了巨大的延伸。】

