掌握 稳定 深刻 数形结合找准计算教学的着力点——《20以内进位加法》素养进阶习题展评与教学建议

文|周利云

一、习题展评

●习题一

1.习题内容

2.能力指向

《数学课程标准（2022年版）》在“符号意识”中指出：要能够理解并且运用符号表示数、数量关系和变化规律，知道使用符号可以进行运算和推理，建立符号意识有助于学生理解符号的使用是数学表达和进行数学思考的重要形式。能将20 以内进位加法的主要算理——“凑十法”的整个过程与点子图一一对应。

3.学情分析

对于20 以内的进位加法，学生往往会存在以下一些不足：一是算理不清，仅仅满足于会计算了即可，至于答案到底是怎么得到的，不加关注；二是算理模糊，或者是相对比较机械。比如一般教师会教学口诀“看大数、拆小数”，但这些并不是唯一的解答方式，比如上题中，拆小数也是可以的，关键要明白这样的框架图背后的算理。

4.具体操作

（1）同学们，哪幅图正确地表示出了小明的想法？请你听清题意之后，独立做出选择。

（2）举手统计选择A 和B 的分别有多少同学。

（3）展开课堂小辩论会：请选择B 的同学来说说理由；请选择A 的同学来反驳。

（4）教师小结：同学们在计算的时候，还是要具体情况具体分析，不能思维定势，要看清楚上面的过程图。

（5）你觉得本题还可以怎样想？请你写一写、画一画。

（6）巩固跟进练习。

给出算式5+8，请你也在纸上分一分，并且画一画点子图，在点子图上表示出你的计算过程。

●习题二

1.习题内容

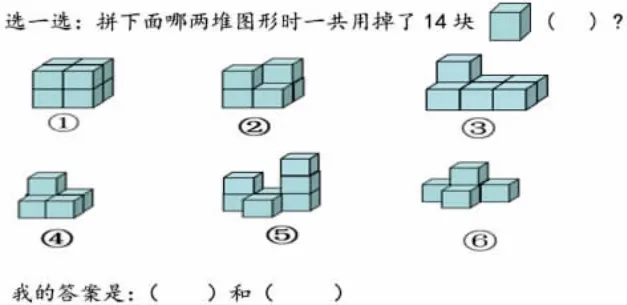
2.能力指向

再一次将计算和图形相挂钩，旨在夯实学生计算能力的同时发展其空间观念。

3.学情分析

本题呈现出三个水平层次。

水平0：认为本题无解。这部分学生只关注眼睛能看得到的，被挡住的均没有考虑。这部分学生占比很少。

水平1：能关注到③号一共是由7 块拼成的，所以与⑤好相加总数等于14 块。但对于②号图形有两种答案，学生仍会存在困难。这样的学生占多数。

水平2： 除了选出③和⑤之外，还能严谨地分析出②号图形其实有两种理解，可以是5 块，也可以是6 块，因此①②相加总数也等于14。

4.具体操作

（1）独立思考：哪两堆图形一共用掉了14 块？

（2）反馈：选择③和⑤的分别数出这两堆图形正方体的个数，得到算式7+7=14。

（3）还有不同意见吗？有学生提出①和②，到底对不对？分成两派展开辩论。

（4）课件演示加学生动手拼搭图形②。

（5）小结：思考问题时，不能只看表面，要把需要解决的问题思考周全，把所有可能的情况都想周到。

（6）你还能和同桌合作，再拼搭出两堆个数之和是14 的不同图形吗？

●习题三

1.习题内容

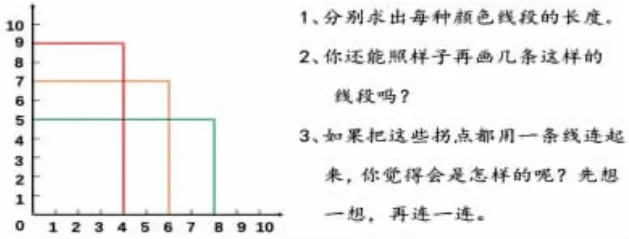
2.能力指向

本题中的第一个任务是要求学生分别求出每种颜色线段的长度。这打破了一般的计算常规形式，使得数与形尽可能结合在一起。在这一过程中，充分培养学生的观察分析能力，明了任何一种颜色线段的长度都是由两个维度上的长度合并而成。本题中的第二个任务是要求学生再照样子画几条这样的线，目的有以下两点：一是培养学生的归纳推理能力，通过第一题的解答，学生应该不难发现这里不同颜色的线段的总长度都是13；二是培养学生学以致用的能力，探索规律并能应用规律，这才是对规律解读正确的打开方式。第三个任务则是埋下函数的种子。

3.学情分析

当学习任务逐步呈现时，学生也能慢慢领悟：原来这些红红绿绿的线还和进位加法有关。在解决最后一个问题时，学生能力悬殊，差异很大，部分学生觉得连不起来，有的仅仅只是单纯连起来而已，并没有发现其中的规律，只有部分学生连起来后感叹数学的奇妙之余还会去分析为何会呈现这样的趋势。

4.具体操作

（1）让学生独立求解每种颜色线段的长度分别是多少。

①每种颜色的两条线段分别多长，你是怎么看出来的？

②检查计算正确与否，否则后续的规律很难被发现。

（2）通过计算，引导发现线段之和都为13，那你还能照样子再画几条这样的线段吗？

（投影学生作品，并让他说说为什么这样画）

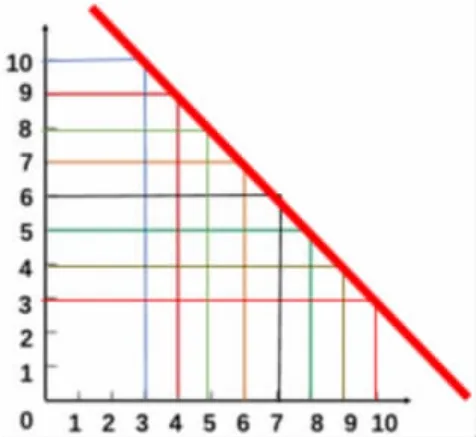
（3）拐点连线，先让学生想象，再动手验证，最后课件呈现。

（4）变式拓展：明白了这些线段和算式之间有着这种联系之后，请你把下面三幅图和对应的算式连一连。

二、分析建议

1.单一概括（一式一图），紧扣计算方法的掌握度

借助一式一图，让每一个算式的计算方法（过程）在各种形象可见的图中变得触手可及。

2.并列概括（一式多图），着眼计算结构的稳定性

在图形题中夹带着计算，既考查了学生计算结构的稳定性，看其是否会受另外因素的干扰，同时在解答过程中也进一步提升了学生有关图形的空间想象等能力。

3.关联概括（一图多式），聚焦计算规律的深刻性

计算规律的深刻性是指计算过程中，善于从繁杂的表面现象中，抓住事物的本质再加以前后推断，并最终找出固有的规律。因此，在计算教学中不应忽视知识点间的有效关联。可以适当借助图形，在有趣形象的图形中发现计算的种种规律，从而帮助学生有效建立起知识网络结构图。