多因素耦合作用对甲烷爆炸特性的影响*

刘可心，刘 炜，孙亚松,2

（1.西北工业大学动力与能源学院，陕西 西安 710072；2.西北工业大学太仓长三角研究院计算物理与能源科学中心，江苏 太仓 215400）

天然气作为清洁高效的低碳化石能源，是中国在2060 年实现碳中和目标的重要过渡燃料[1-2]。中国天然气储量丰富且市场需求巨大，中国国家能源局预计在2030 年中国的天然气消费规模将达到5 500～6 000 亿立方米[3]。然而，天然气在生产、运输和储存等环节都存在潜在的爆炸风险，可能对人们的生命和财产安全造成严重威胁。此外，基于天然气优良的理化特性以及日趋成熟的相关配套技术，天然气在内燃机和发电机等设备中的应用越来越广泛，天然气在这些复杂应用场景下的高效利用和安全问题也越来越受到人们的关注。在天然气的诸多成分中，甲烷气体含量最高且爆炸风险最大[4]。因此，开展甲烷爆炸特性的研究对于天然气的安全高效利用和爆炸防控具有重要意义。

在可燃气体爆炸特性的研究中，当量比φ、温度T0和压力p0等初始条件是影响爆炸特性的重要因素[5-7]。在当量比因素研究方面，余明高等[8]研究了室温下不同甲烷体积分数的甲烷-空气混合物在管道内的爆炸特性，得出甲烷体积分数为9.5%时，即化学当量比条件下，甲烷的最大爆炸压力和最大爆炸压力上升速率最大，且峰值出现的时间最早；王文涛等[9]探究了常温常压下不同当量比对于乙炔-空气爆炸特性的影响，研究发现随着当量比增大，最大爆炸压力先升高后下降，在当量比为1.32 时达到峰值；Tran 等[10]利用ANSYS Fluent 软件，对于合成气-空气混合物在不同当量比（0.8～3.0）下的爆炸行为进行了数值模拟研究。在压力因素研究方面，王华等[11]采用20 L 近球型爆炸反应器，分析了不同初始压力对于可燃性气体爆炸特性的影响，研究表明初始压力对于最大爆炸压力和最大压力上升速率具有促进作用，会导致爆炸危险性增强；Huang 等[12]使用645 mL 的圆柱形容器，在室温高压条件下进行了甲烷-空气混合物的爆炸实验；Cui 等[13]测量了甲烷-空气混合物在低温（123～273 K）和高压（0.1～0.9 MPa）条件下的可燃极限，得到了温度和压力对于可燃极限的影响规律。在温度因素研究方面，高娜等[14]研究了常压下初始温度对甲烷-空气混合物爆炸压力的影响，揭示了初始温度对于最大爆炸压力的抑制作用；Cammarota 等[15]研究了化学当量条件下甲烷-空气混合物的爆炸特性，发现初始温度的增加对燃烧速度具有促进作用，进而提高了最大压力上升速率和爆燃指数KG；李润之等[16]基于流场模拟平台，利用数值模拟手段深入剖析了低温环境条件下甲烷的爆炸过程。此外，容器尺寸[17]、障碍物[18-19]、湍流[20]等因素也会对甲烷的爆炸特性产生影响。

综上所述，目前针对爆炸特性方面的研究主要集中在单因素分析上，温度和压力条件也多为常温常压或者单一的高温或高压，且当量比大多数为1.0，对于复杂工况如高温高压、高温富燃料等情况下的爆炸特性研究较少。但在实际工程应用中，可燃气体的爆炸特性往往会受到多种因素的耦合作用。以天然气内燃机为例，其反应过程涉及到不同的当量比、温度以及压力耦合条件。然而，目前关于多因素耦合作用对甲烷爆炸特性影响的研究鲜有报道，并且对于复杂条件下各因素间的相互作用关系也缺乏深入了解。值得注意的是，发动机的整体环境性能和技术经济性能是建立在具有较高耐爆性能基础上的[21]，因此研究多因素耦合条件下甲烷的爆炸特性对于天然气内燃机以及天然气发电机等设备的防爆设计和安全应用是至关重要的[22]。

最大爆炸压力pmax是评价爆炸特性的关键参数，能够最直观地反映爆炸的危险程度[23]。基于此，本文选取pmax作为切入点，探究初始温度T0和初始压力p0耦合、初始压力p0和当量比φ耦合以及初始温度T0和当量比φ耦合3 种条件对于甲烷爆炸特性的影响，并建立pmax的三因素回归预测模型，得到pmax与φ、T0和p0之间的数学关系，以期实现对于复杂条件下甲烷爆炸特性的预测，为甲烷反应容器的强度设计和安全距离预留提供数据参考。

1 实验系统与方法

1.1 实验装置

实验装置由配气系统、加热系统、点火系统和数据采集系统等组成，装置示意图如图1 所示。本实验采用立式不锈钢圆柱作为爆炸容器，容器的直径为80 mm，高度为243 mm，极限承压为10 MPa。配气系统包括真空泵和高压气瓶，其中甲烷纯度为99.99%，配气可通过电磁阀实现自动控制，精度为0.1%。加热系统通过缠绕在容器周围的电阻丝进行加热，通过PID 系统实现温度调控。采用四线制铂电阻PT100 作为温度传感器进行测温，最大量程为350 ℃，温度的稳定性和均匀性均优于±2 ℃。点火系统采用电火花放电，使用电压为15 kV、最大通过电流为30 mA 的变压器作为点火电源，点火能量约为10 J，点火时间0.4 s。点火电极由2 个直径为1 mm 的不锈钢制成，间距3 mm，置于容器几何中心处。数据采集系统由PCB 高频压力传感器和计算机组成，压力传感器置于爆炸容器顶部，最大量程为5 MPa，精度为0.1%。

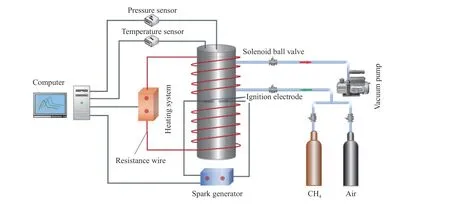
图1 实验系统示意图Fig.1 Schematic diagram of experimental system

1.2 实验方法

当量比定义如下：

式中：(F/A)st为化学计量比下的甲烷与空气体积分数之比；F/A为实际的甲烷与空气体积分数之比。

本文将φ设置为0.6、0.8、1.0、1.2 和1.4，对应的甲烷体积分数分别为5.93%、7.75%、9.50%、11.19%和12.81%，其中φ=1.0 为化学当量比。另外，选取25、50、100、150 和200 ℃作为初始温度T0，选取0.1、0.2、0.3、0.4 和0.5 MPa 作为初始压力p0。

在实验开始前，首先检查装置气密性，以保证气密性良好。通过加热系统将爆炸容器的温度升高至预设的实验温度。然后，使用真空泵将爆炸容器抽真空至-0.1 MPa，采用道尔顿分压法按照预定比例对混合气体进行配置。为确保点火前甲烷/空气混合物在爆炸容器中处于静止平衡状态，混合气体在容器中至少停留10 min。点火完成后，压力传感器采集的动态压力数据由计算机进行处理，最后得到甲烷的爆炸压力-时间曲线和pmax。每次实验结束后，连续抽真空3 次，清除容器内的所有废气。为保证实验的可重复性和准确性，每个工况至少进行3 次重复测试。

2 双因素耦合条件下甲烷爆炸特性分析

2.1 初始温度和初始压力耦合

图2 展示了φ=1.0 时，在T0和p0的影响下，pmax的变化情况。从图2(a)可以看出，pmax与p0呈正比。从斜率来看，T0升高，pmax随p0的增长速度逐渐降低。当p0升高时，升温对于pmax的抑制作用会被强化。这是由于温度越高，混合气中的甲烷分子数目越少。同时与低压相比，在高压情况下混合气中的空气分子数目大幅增加，空气的惰化效应会加强高温对于pmax的抑制效果[24]。由图2(b)可知，pmax与T0呈反比，变化趋势基本相同。从斜率来看，p0越高，pmax随T0的下降速度越快。当T0升高时，升压对于pmax的促进作用会被削弱。造成这种现象的原因是随着温度的升高，混合气中的甲烷分子数目和氧气分子数目均逐渐减少，甲烷分子与氧气分子发生有效碰撞的概率随之降低[25]，从而削弱了高压对于pmax的促进效果。

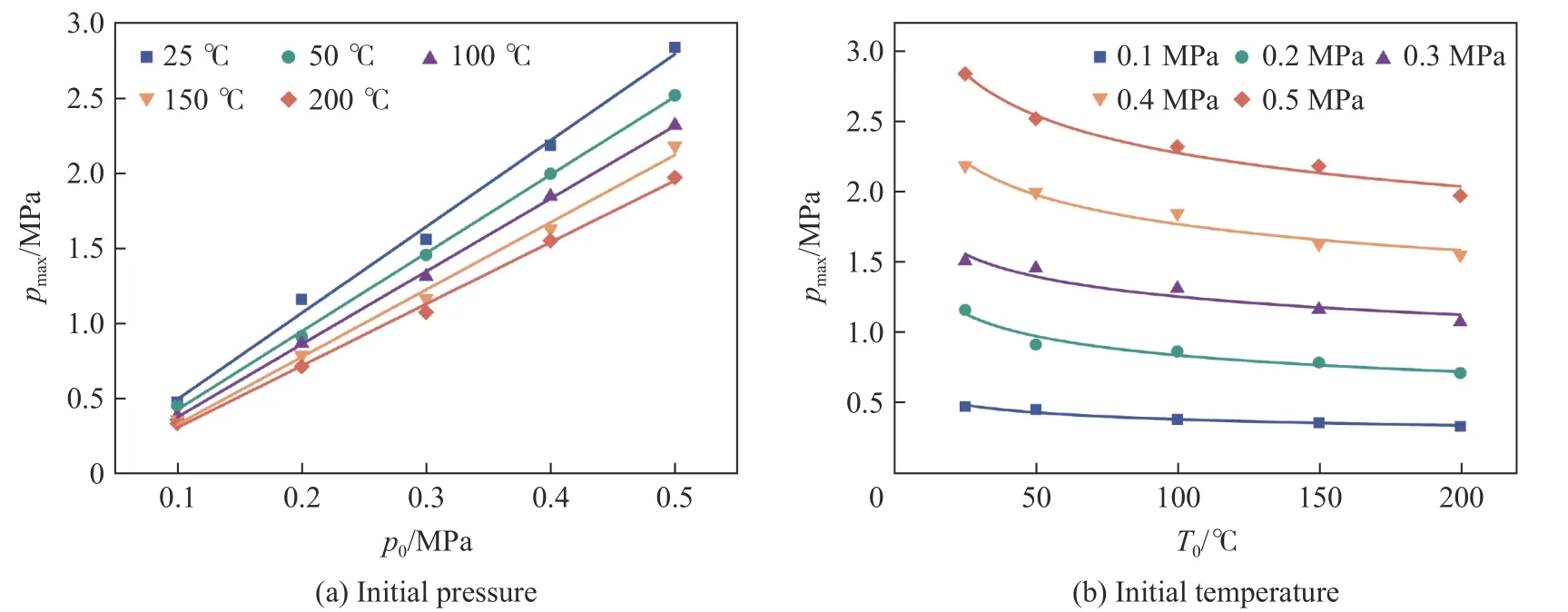
图2 T0 和p0 对pmax 的影响Fig.2 Effect of T0 and p0 on pmax

如图3 所示，为了更直观地体现T0和p0对pmax的耦合影响，通过拟合得到pmax随T0和p0变化的三维非线性曲面。从图中可以看出，在常温高压（25 ℃、0.5 MPa）情况下甲烷的pmax最高，在高温常压（200 ℃、0.1 MPa）情况下甲烷的pmax最低，所以在生产实际中需注意常压高温情况下甲烷的防爆安全问题。

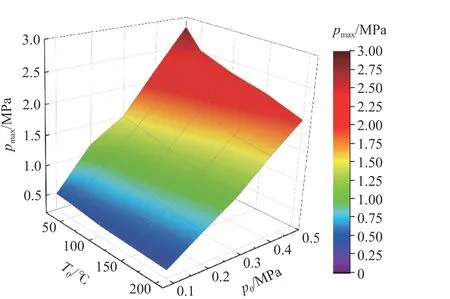
图3 T0 和p0 对pmax 耦合影响Fig.3 Coupling effects of T0 and p0 on pmax

为了定量评估T0和p0耦合作用对于pmax的影响，利用Origin 软件得到如下拟合函数：

式中：z0、A、B、C、D、F为拟合系数，具体数值见表1。从表1 可以看出，在不同φ条件下，决定系数R2均大于0.99，具有较好的拟合效果。利用式(2)可预估在实验温度和压力范围内(25 ℃≤T0≤200 ℃，0.1 MPa≤p0≤0.5 MPa)，不同φ条件下甲烷的pmax。

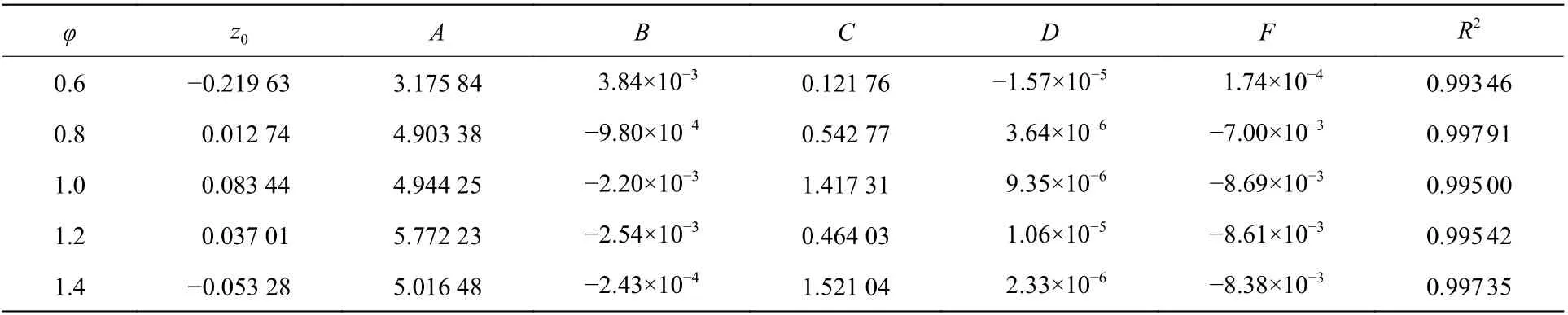
表1 拟合函数的各项参数Table 1 The parameters of the fitting function

2.2 初始压力和当量比耦合

为了定量评估p0和φ的耦合作用对于pmax的影响，现定义如下参数：pmax差值为：

图4 展示了T0=100 ℃时，在p0和φ影响下，pmax的变化情况。结合图4(a)和图4(b)不难发现，在φ=1.2 时，pmax达到峰值且随p0的增长速度最快。这说明在φ=1.2 时，甲烷的爆炸反应最充分，危险程度最高。出现这种现象的原因是：化学反应具有不完全性，并且燃烧产物也会发生解离及二次反应，因此气体的最佳爆炸当量比一般会大于化学计量比，且为化学计量比的1.1～1.5 倍[26]。

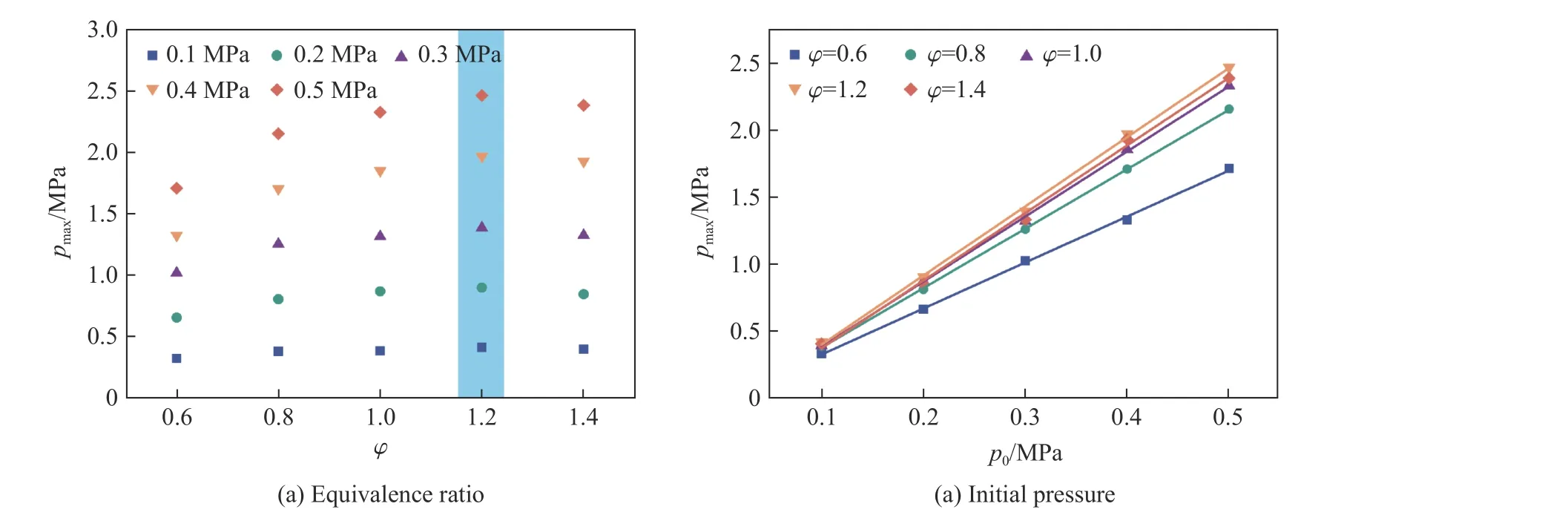
图4 p0、φ 对pmax 的影响Fig.4 Effect of p0 and φ on pmax

为了探究不同φ条件下，p0的变化对于pmax的影响规律，通过计算得出的a13、a23和Sa随φ的变化曲线如图5 所示。从图中可以看出：a13和a23随φ的变化规律较一致，均为先升高后降低，且峰值均出现在φ=1.2 处。Sa随φ先减小后增大，当φ=1.0 时，Sa达到最小值，表明此时p0的变化对于pmax的影响最小；当φ=0.9 或1.2 时，a13、a23相同且Sa为1，说明p0的变化对pmax的影响呈线性变化；当0.9＜φ＜1.2 时，Sa＜1，表明低压环境对pmax的影响更大；当φ＜0.9 或φ＞1.2 时，Sa＞1，说明对于较稀可燃混合气和较浓可燃混合气，高压环境对pmax的影响更大。

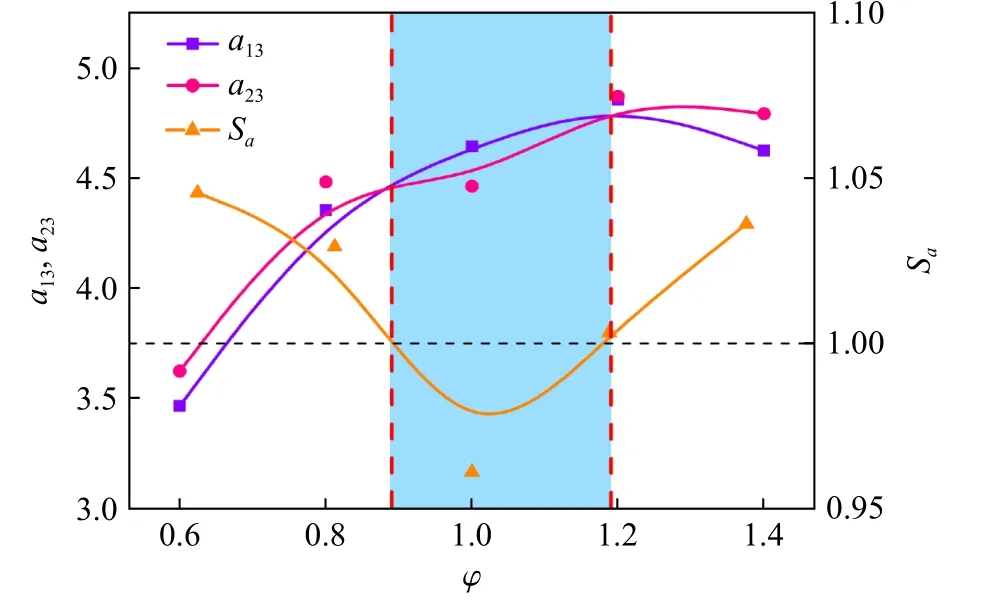
图5 a13、a23 和Sa 随φ 的变化曲线Fig.5 Variation curves of a13, a23 and Sa with φ

2.3 初始温度和当量比耦合

在研究T0和φ对于pmax的耦合影响时，研究对象选择p0=0.5 MPa，T0=25, 50 和100 ℃时对应的pmax，参数定义方法与前文类似，此处不再赘述，其中pmax变化率和pmax变化率的比值分别用b13、b23和Sb表示。

图6 展示了p0=0.5 MPa 时，在T0和φ影响下，甲烷-空气混合物pmax的变化情况。如图6(a)所示，在不同T0下，pmax均在φ=1.2 处达到最大，这与上文提到的原因一致。观察图6(b)可见，当φ=0.6 时，随着T0升高，pmax先上升后下降，在100 ℃时达到峰值，而其他φ条件下pmax均单调递减。这可能是因为：温度对于爆炸的影响体现在两个方面，一方面温度的升高会加快分子的运动速率，提高分子间的碰撞频率；另一方面温度的升高会减少分子的数目，降低分子间的碰撞频率。受这两方面的共同影响，当T0＜100 ℃时，温度对于爆炸的促进作用要强于抑制作用；当T0＞100 ℃时则正好相反。具体影响机理需要通过爆炸模拟等手段进一步探究。

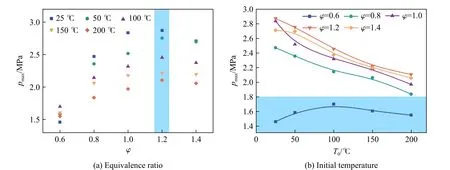
图6 T0、φ 对pmax 的影响Fig.6 Effects of T0 and φ on pmax

为了探究不同φ条件下，T0的变化对于pmax的影响规律，通过计算得出的b13、b23和Sb随φ的变化曲线如图7 所示。从图中可以看出：b13和b23随φ的变化规律有所差异，b13先增加后减小，而b23单调递增。Sb随φ先增大后减小再增大，在φ=1.0 时，Sb达到最小值，表明此时T0的变化对于pmax的影响最小；当φ=1.15 时，b13，b23相同即Sb=1，表明T0的变化对pmax的影响呈线性变化；当φ＜1.15 时，Sb＜1，表明T0越低，pmax的变化越显著；当φ＞1.15 时，Sb＞1，表明T0越高，pmax的变化越显著。另外，当φ＞1.0 时，Sb急剧上升，表明富燃料状态下pmax变化加剧。

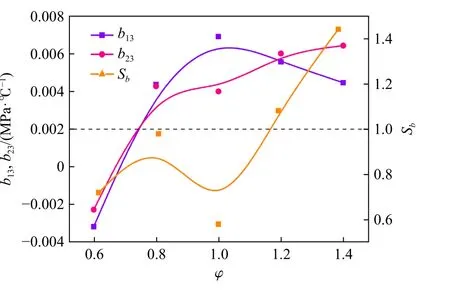
图7 b13、b23 和Sb 随φ 的变化Fig.7 Variation of b13, b23 and Sb with φ

3 三因素耦合条件下 pmax 预测模型的建立与验证

3.1 预测模型的建立

1stOpt 是一款数值优化分析计算软件，具有超强的寻优、容错能力，在非线性回归、曲线拟合等领域得到了广泛应用[27]。为了得到pmax的预测模型，利用1stOpt 中的Levenberg-Marquardt 算法+通用全局优化算法对实验数据进行快速拟合，并将决定系数R2和均方根误差ξ 作为评价模型拟合效果的基本指标，其中R2能够反映模型的拟合优度，均方根误差能够反映模型的预测偏差。具体的计算公式为：

式中：n为数据样本数目，xi为任意变量x的实测值，xˆi为x的预测值，x¯ 为x的平均值。

利用实验所得的125 组数据建立pmax预测样本集，将样本集与1stOpt 软件内置拟合库中的函数进行逐一拟合，并得到相应的基本评价指标。表2 为筛选出的一部分拟合效果较好的公式（其中压力单位为MPa）。通过对比可以看出：式(1)的R2大于0.99 且预测偏差最小，说明选择该公式作为预测模型是合理可靠的，最能体现pmax与各参数之间的关系。

表2 不同公式拟合条件下的评价指标对比Table 2 Comparison of evaluation indicators under different formula fitting conditions

3.2 预测模型的验证

图8 为pmax模型预测值与实验测试值的拟合结果。从图8(a)中可以看出：前25 组数据拟合效果较差，这是因为φ=0.6 时pmax的变化规律与φ取其他值时有所差异导致的。在φ取其他值时，预测值与实测值均拟合良好，并且随着φ的增加，预测模型的拟合更加精确，这表明该预测模型较为可信，且更加适用于高当量比条件。

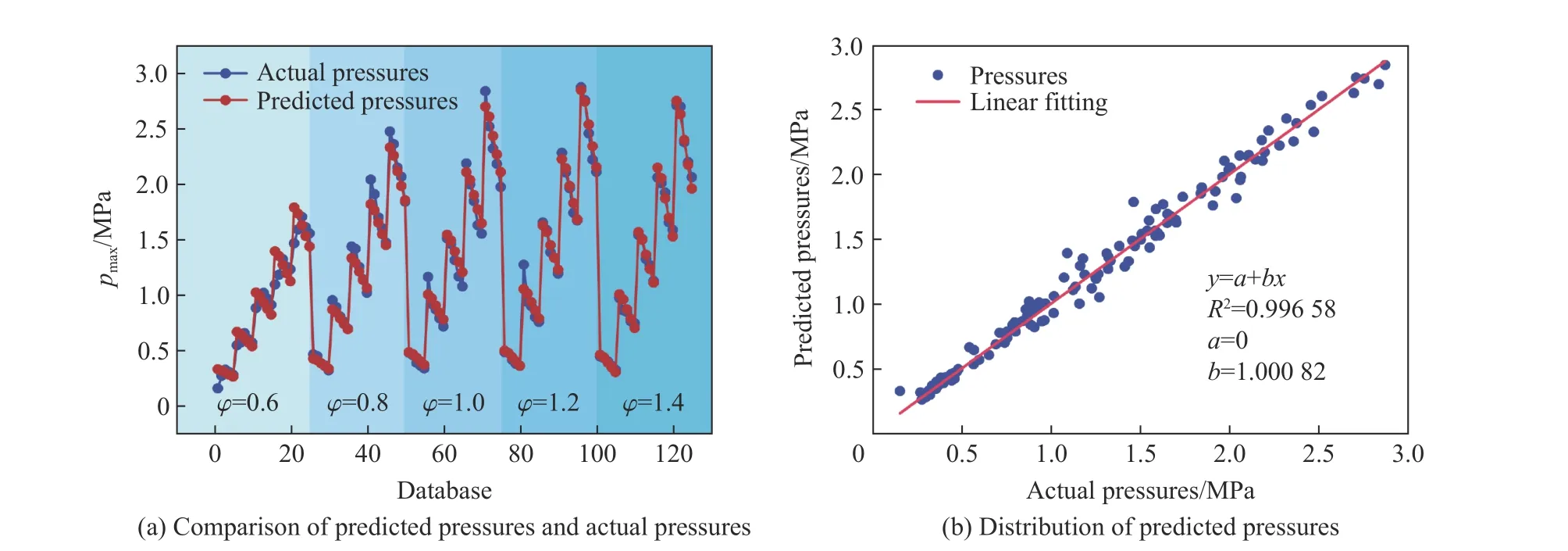
图8 最大爆炸压力预测值与实际值的拟合结果Fig.8 Fitting results of predicted values and actual values of maximum explosion pressure

图8(b)中，y表示模型预测的pmax，x表示实测的pmax，使用直线方程y=a+bx进行线性回归。若a越接近0、b越接近1，则模型拟合程度越好。在图8(b)中，线性回归方程的a=0,b=1.000 82，说明方程拟合程度良好，模型具有较好的预测效果。

为了验证模型在其他工况下是否适用，利用拉丁超立方抽样法选取了6 组工况，涵盖了不同的φ、T0以及p0，以保证抽样的全面性。将基于1stOpt 模型的预测结果与实验测试结果进行对比，结果如表3所示。从表中可以发现，预测结果与实验结果较为接近，相对误差均小于10%。这说明在本文的实验条件（0.1 MPa≤p0≤0.5 MPa，25 °C≤T0≤200 °C，0.6≤φ≤1.4）下，该预测模型能够较好的实现对于甲烷pmax的预测。

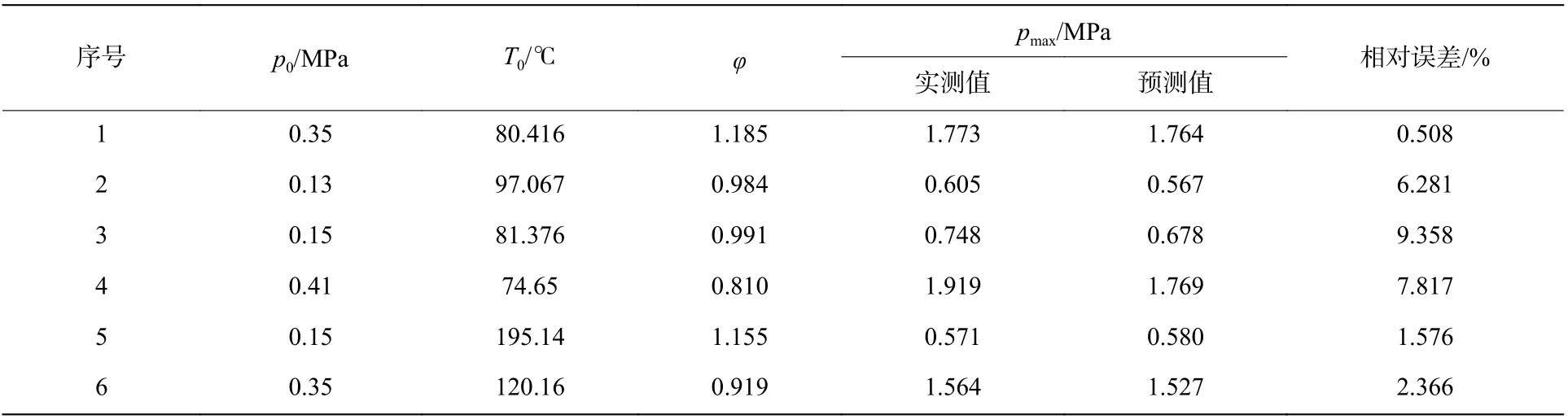
表3 模型预测结果与实验结果对比Table 3 Comparison between the prediction results and the experimental results

4 结 论

(1) 初始温度和初始压力耦合条件下，随着初始压力的升高，初始温度对pmax的影响程度增强；随着初始温度的升高，初始压力对pmax的影响程度减弱。

(2) 初始压力和当量比耦合条件下，在研究的实验条件范围内，当0.9＜φ＜1.2 时，低压环境对pmax影响更大；当φ＜0.9 和φ＞1.2 时，高压环境对pmax影响更大。

(3) 初始温度和当量比耦合条件下，在研究的实验条件范围内，当φ＜1.15 时，低温环境对pmax影响更大；当φ＞1.15 时，高温环境对pmax影响更大。另外，富燃料状态下pmax变化加剧。

(4) 本文所建立的数学模型精度较高，适应性较好，可实现实验条件范围内对于甲烷pmax的预测。