基于时间跨度注意力机制的多变量时间序列预测方法

李文豪，严 华

（四川大学电子信息学院，成都 610065）

0 引言

多变量时间序列预测已被广泛应用于交通预测［1-2］、汇率预测［3］、用电消耗预测［4-5］、河流水位预测［6］等领域。如果能实现精准的预测并应用在这些领域，将会帮助人们进行重大决策。

多变量时间序列预测的关键是充分捕获其长、短期的依赖。现实世界的应用通常需要短期和长期重复模式的混合［7］。然而传统的方法，例如线性移动平均模型［8］、支持向量机线性回归［9］大多采用统计模型来研究时间序列的演化，可能无法捕捉到复杂的潜在非线性关系［10］。递归神经网络（RNN）［11］是一种专为序列建模而设计的深度神经网络，因其在捕捉非线性关系方面的灵活性而受到广泛关注。DA‑RNN［12］使用了RNN 来捕捉时间序列的长期时间依赖，但它没有使用专门的方法来提取时间序列的短期模式。在计算机视觉领域，卷积神经网络（CNN）［13‑14］模型通过成功提取局部和平移不变特征表现出了在输入图像的不同粒度级别方面的出色性能。LSTNet［7］利用了CNN 的长处去发现多维输入变量之间的短期模式。然而，与LSTNet 相同，近年来提出的网络MTNet［10］和TPA［15］都只使用了一种大小的卷积核来提取多变量时间序列的短期模式，这使得时间序列的短期模式并没有被充分提取。

仅仅将不同时间跨度的短期模式提取出来还不够，还要选择性地加以利用。因为在对不同的数据集和预测范围进行预测时，模型对不同时间跨度的短期模式的依赖是不同的。虽然MTGNN［16］使用了不同尺寸CNN 卷积核来提取不同范围内的时间特征，但是没有对不同卷积输出进行选择，而是将它们不加区分地拼接在一起。

针对上述问题，本文提出了基于多尺度特征表示和时间跨度注意力的网络结构。多变量时间序列首先经过包含多尺寸卷积核的CNN 模块来获得不同时间跨度的短期模式，然后通过时间跨度注意力模块来为短期模式分配权重。之后，将时间跨度注意力模块的输出送入RNN模块来进一步提取长期模式。与LSTNet 相同，本文也引入了线性回归模块来提高模型的鲁棒性。但与LSTNet 直接将非线性部分和线性部分的输出相加不同，本文采用了一个权重学习模块来整合非线性部分和线性部分的输出。在四个公开数据集上的实验结果表明，本文提出的模型能有效提高多变量时间序列预测的准确度。

1 TSANN

1.1 概述

本文提出的时间跨度注意力神经网络（a deep neural network based time span attention，TSANN）的结构如图1所示。其主体结构分为线性和非线性两部分。在非线性部分，将多变量时间序列数据输入到有多个分支的多尺度卷积模块来提取不同时间跨度的短期模式。多个分支的输出被裁剪成相同尺寸后在通道维度上拼接。之后，多尺度卷积模块的输出被送入不同的短期模式赋予权重的时间跨度注意力模块。图1中时间跨度注意力模块的输出被赋予了不同的权重。然后，时间跨度注意力模块的输出被送入迭代模块进一步提取长期模式。最后，通过全连接层得到非线性部分的输出。

图1 时间跨度注意力神经网络

取非线性部分输入中近期的数据作为线性部分的输入。线性部分的输出通过简单的AR 模块得到。最后，通过权重学习模块将两部分的输出加起来得到最后的预测结果。

1.2 多尺度卷积模块

多尺度卷积模块的目标在于充分提取时间维度上不同时间跨度的短期时间模式和变量间的局部依赖。在该模块的多个CNN 分支中，不同分支间CNN 卷积核宽度w不同，高度n相同。其中w表示不同的时间跨度，n表示变量个数。这样，模型就能提取到多时间跨度的短期模式。

多尺度卷积模块中包含6 个分支，其卷积核宽度w分别为｛3，6，7，12，24，36｝。每个分支中都设置N个相同的卷积核。下文通过实验说明w设置的依据。第k个分支中的第i个卷积核扫描输入矩阵X，并产生如下关系：

其中：*表示卷积操作，输出hki是一个向量，RELU函数为RELU(x)=max(0,x)。

1.3 时间跨度注意力模块

当预测任务不同时（数据集不同或预测时间步长Q不同），网络模型对不同时间跨度的短期模式的依赖是不同的，所以要对不同时间跨度的短期模式进行选择性的利用。

多尺度卷积模块一共提取到了6种不同时间跨度的短期模式，每种短期模式有4个通道。所以卷积模块的输出一共有24 个通道，表示为H∈R24×T×1。时间跨度注意力推断出一个一维通道注意地图Ms∈R24×1×1。整体注意过程可以概括为

其中，⊗表示元素级相乘。

图2 描述了时间跨度注意力图的计算过程。时间跨度注意力计算公式为

图2 时间跨度注意力模块示意图

其中，σ表示sigmoid函数。

1.4 循环神经网络模块

在经过多尺度卷积模块和时间跨度注意力模块之后，模型已经提取到了不同重要程度的短期模式。但时间序列中还存在更为长期的依赖关系，能帮助提高预测的准确度。本文使用了擅长记忆历史信息的GRU［17］来组成循环神经网络模块。

时间跨度注意力模块的输出被输入到循环模块中。在时间为t时，循环单元的隐藏状态计算公式为

其中：⊗表示元素级相乘；σ表示激活函数；xt为模块在时间t时的输出。

1.5 权重学习模块

预测结果的准确度不仅依赖于长期数据中包含的周期，也依赖于短期数据的线性关系。目前使用线性和非线性两部分进行预测的网络，都是直接将两部分的预测结果相加得到最终预测结果，但是这样做忽略了预测结果对两者的依赖程度。为了更加准确地表示预测结果对线性部分和非线性部分的依赖关系并提高预测精度，本文设计了权重学习模块。该模块包含两个可学习参数，分别来学习对线性和非线性部分的依赖程度。TSANN最终的预测结果计算如下：

其中，α和β为两个可学习的参数。

2 实验

为了验证TSANN 的有效性，本文将TSANN在四个常用基准数据集上与八种方法进行了对比，其中包括四种传统方法和四种近几年提出来的先进方法。

2.1 数据集描述

LSTNet 发布了四个公开可用的多元基准数据集。表1展示了数据集的相关统计信息。为了便于验证，所有的数据集按照时间顺序分为训练集（60%）、验证集（20%）和测试集（20%）。

表1 四个基准数据集的描述信息

2.2 对比方法

参与比较的九种方法的描述如下：

AR：一个标准的自回归模型。

LRidge：具有L2 正则化的向量自回归模型，曾经是最流行的多元时间序列预测模型。

GP：用于时间序列预测的高斯过程模型［18‑19］。

RNN⁃GRU：使用GRU单元的RNN模型。

LSTNet：使用CNN 提取短期模式和使用RNN提取长期模式的模型［7］。

MTNet：一种使用记忆网络捕捉极长期模式的模型［10］。

TPA：使用时间模式注意力来选择相关时间序列的模型，并使用其频域信息进行多元预测［15］。

MTGNN：使用图神经网络和图学习模块自动提取变量之间的单向关系的模型［16］。

TSANN：本文提出的模型。

对于前面提到的单值输出方法，例如GP、LRidge 和AR，本文为每个变量训练一个模型。例如Solar‑Energy 数据集有137 个变量，因此本文总共训练了137个模型。

2.3 实验指标

由于在相同的数据集上对TSANN与LSTNet、MTNet、TPA 和MTGNN 进行比较，因此继续使用相同的评估指标：RSE和CORR。

根相对平方误差（RSE）：

经验相关系数（CORR）：

其中：Y表示真实值；表示模型的预测值。对于RSE，值越低越好；而对于CORR，值越高越好。

2.4 实验结果

表2列出了所有实验的结果。遵循以往的惯常做法，设置Q={3,6,12,24}，并使用RSE和CORR两个指标来评估模型。Q越大，预测难度越大。在表2中，每个数据集和每个指标的最优结果被加粗突出显示。在所有的32 个最优结果中，TSANN 占了19 个，远多于其他方法，证明了本文提出方法的优越性。在其他方法中，MTGNN 的 最优结果 占了10 个，TPA 占 了2 个，LRidge占了1个。

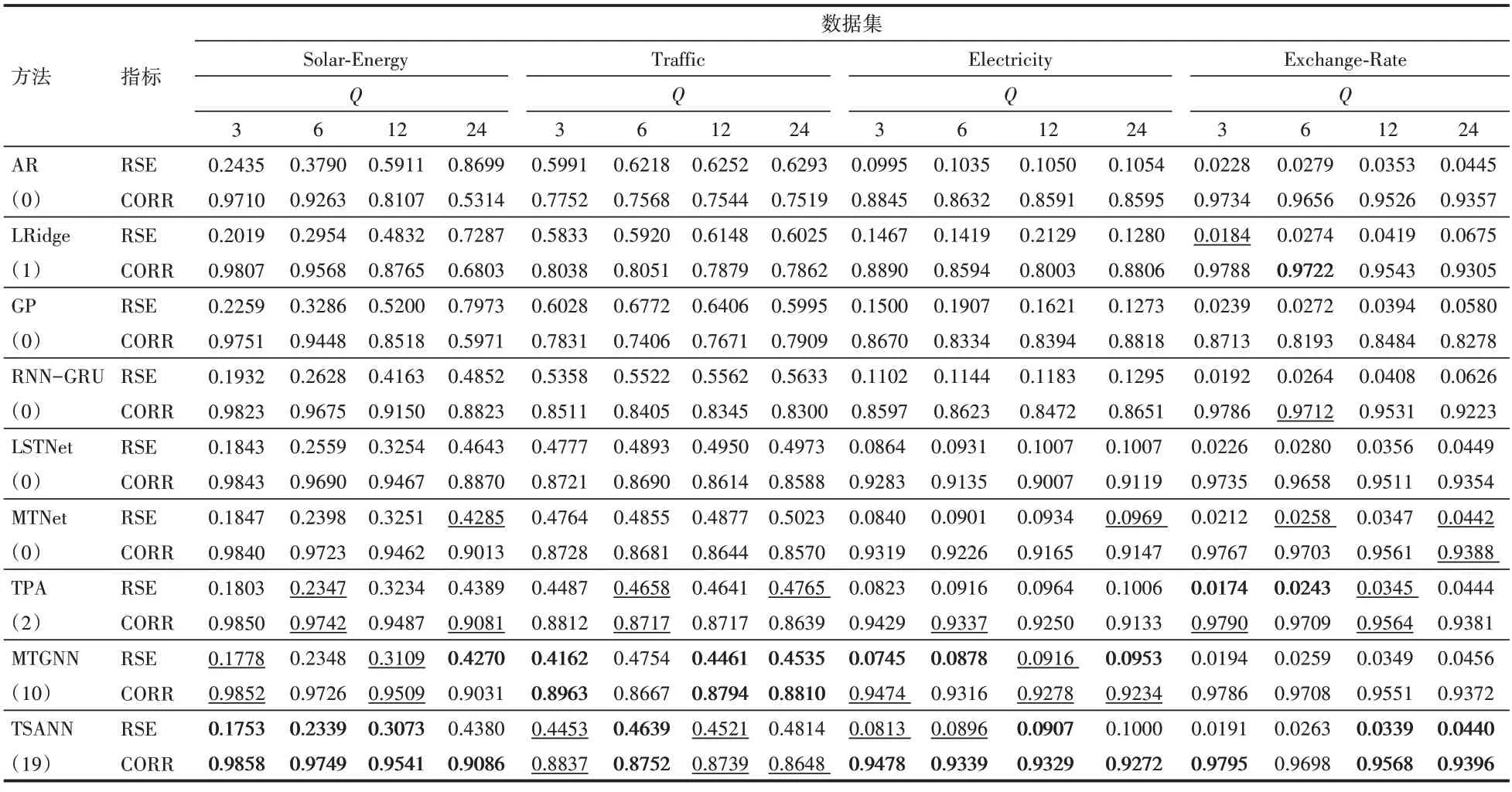
表2 九种方法在四个数据集上的对比实验结果

TSANN之所以能取得优于其他方法的结果，主要是因为使用了多尺度卷积模块来充分提取多变量时间序列的短期模式，并使用时间跨度注意模块进行选择性的利用。

文献［7］对这四个数据集进行了分析，发现Solar‑Energy、Traffic 和Electricity 都具有明显的周期性，而Exchange‑Rate 则没有。LSTNet 在Exchange‑Rate 上的表现不如AR、LRidge 等传统方法，是因为线性模型比深度学习方法更适合该数据集。本文提出的方法能在Exchange‑Rate上取得最优结果，是因为使用了权重学习模块，能够根据不同数据集动态调整模型对线性模块和非线性模块的依赖程度。

本文方法在Traffic 数据集上的表现不如MTGNN，可能是因为MTGNN 使用了图神经网络，使其具有更强的提取变量间依赖关系的能力。在这四个数据集中，Traffic具有最多的变量数（862），而MTGNN 中复杂的图神经网络在变量数较大时表现出了一定的优势。

2.5 消融实验

为了验证本文所提方法中关键模块的有效性，在Solar-Energy 数据集上进行了充分的消融实验，每次移除TSANN 中的一个模块，并将它们命名如下。

w/o MC：TSANN 去除多尺度卷积模块。按照LSTNet 的设置，只使用宽度为6 的CNN 卷积核来代替多尺度卷积模块进行短期模式的提取。

w/o TSA：TSANN 去除时间跨度注意力模块。不同时间跨度的短期模式被不加选择地利用。

w/o WL：TSANN 去除权重学习模块。将线性部分和非线性部分的输出直接相加。

w/o AR：TSANN 去除线性模块。预测结果仅由非线性部分输出得到。

在进行消融实验时，Q取难度最大值24。实验结果如表3所示。

表3 消融实验结果

消融实验结果表明，TSANN 引入的关键模块都提升了网络结构的性能。多尺度卷积模块的引入极大地提升了实验结果，因为它能充分提取不同时间跨度的短期模式来帮助模型进行预测。权重学习模块带来的效果也很明显，因为它能调整最终预测结果对线性部分预测结果和非线性部分预测结果的依赖关系，实现更准确的预测。实验结果也进一步验证了LSTNet 中提出的AR 模块的有效性。时间跨度注意力模块在多尺度卷积模块的基础上进一步提升了预测结果的准确度，因为它对不同时间跨度的短期模式进行了选择性的利用。

3 结语

本文提出了一种基于多尺度卷积和时间跨度注意力的深度学习框架（TSANN），来进行多变量时间序列的预测。TSANN 中的多尺度卷积模块能充分提取时间序列的短期模式。时间跨度注意力模块能对这些短期模式进行选择性的利用，以应对不同的数据集和未来时间步Q。另外，权重学习模块能动态调整最终预测结果对线性和非线性输出的依赖程度，从而提高预测精度。大量的实验在四个公开数据集上进行，实验结果证明了本文方法的有效性。

本文中短期模式的时间跨度是通过实验确定的。未来的工作将致力于找到一种能根据数据集和未来时间步Q自动确定时间跨度的方法。