基于拟合的混响室莱斯K因子预测及信道重建

张雪莹，赵 翔

（四川大学电子信息学院，成都 610000）

0 引言

有别于有线通信系统，无线通信系统的信号在开放的空间中传播，这种开放性导致无线信道具有随机衰落及多径传输的特点。混响室由于其四壁、天花板、地板及搅拌器可使信号在腔室内进行多次反射而天然地具备模拟多径、随机电磁环境的能力［1］。此外，相较于真实场景，在混响室中进行无线信道的测量具有更高的可靠性和可重复性。因此，混响室常被用于对无线信道进行模拟及研究。例如，电磁兼容（EMC）中使用混响室模拟了瑞利衰落信道，该模型描述了发射机与接收机之间不存在直射信号的无线信道。通过重新配置混响室可以模拟更多随机电磁环境。

莱斯衰落信道是一种常见的无线传播环境，它适用于收发信机之间存在直射信号的情况。莱斯K因子是莱斯传播信道的关键参数之一，它反映了接收信号的直射分量和散射分量的相对强度。混响室中的莱斯K因子受收发天线间的距离、混响室品质因数等因素影响，通过改变混响室的配置，可以改变莱斯K因子的大小。2006年，Holloway等［2］在混响室中对具有不同莱斯K因子的衰落环境进行了模拟，同时对天线和腔体特性对K因子的函数关系进行了研究；2011 年，Lemoine 等［3］通过蒙特卡罗模拟和混响室实验改进了K因子估计的解析表达式，并将测量结果与Friis 传输公式的计算结果进行了对比；2018 年，Marvin 等［4］采用源搅拌和机械搅拌的方式对混响室中的莱斯K因子进行了测量。

已有的文献多是对给定的不同配置情况下的混响室莱斯K因子值的测量、计算及对比问题进行的研究，而没有对莱斯K因子的预测及如何由给定的莱斯K因子进行信道重建的问题进行研究。当研究者需要获取不同配置下的混响室莱斯K因子数值时，对莱斯K因子进行预测可节省大量的研究时间及人力物力。此外，在对具有特定莱斯K因子的无线信道进行研究时，如何根据给定的莱斯K因子进行信道重建的问题变得尤为重要。

针对K因子的快速预测及给定K因子的信道重建问题，本文提出了基于拟合的混响室莱斯K因子预测及信道重建的方法，以不同收发天线间距离处的莱斯K因子值的预测及信道重建问题为例进行了研究。此方法不仅可以简单快速地得到所需距离处的莱斯K因子，还可以为如何配置给定莱斯K因子的混响室给出建议，为后续的混响室研究提供了便利。该方法还可扩展到对于如混响室品质因数等其它因素的不同取值处的莱斯K因子预测及信道重建问题中，具有普适性。此外，本文使用了几种不同的拟合函数对实测数据进行了拟合，并从物理意义、拟合误差等多个角度进行了讨论及比较。

1 无线信道莱斯K因子分析

2006年，Holloway等［2］推导了混响室中的莱斯K因子表达式，如式（1）所示：

式中：V为混响室体积；λ为波长；Q为混响室品质因数；r为收发天线间距离；Dt为发射天线的方向性；Dr为接收天线的方向性，文献［2］将Dt、Dr假设为Dt(θ,φ)、Dr(θ,φ)，即远场方向性。为发射天线和接收天线的极化方向单位矢量。此表达式体现了混响室特性、天线方向性等因素与莱斯K因子之间的关系。通过改变混响室的特性或腔内的天线配置，可以实现具有所需莱斯K因子的信道。

在混响室中对收发天线间的散射参数进行测量及后处理，可得到莱斯K因子的值。在S21的散点图中可以直观地感受到直射分量及散射分量对莱斯K因子的影响，如图1所示。当直射分量不显著时，不同搅拌器位置的数据聚集在一个以原点为中心的圆中，如图1（a）所示。当直射分量明显占优时，数据点簇将远离原点，如图1（b）所示。莱斯K因子的计算公式如式（2）［2］所示。

2 拟合原始数据获取

首先通过少量测量获取莱斯K因子拟合所需的原始数据。混响室由腔室和搅拌器组成。本文所使用混响室的尺寸为3.97 m × 2.8 m ×1.91 m，混响室中使用非规则铝箔搅拌器。腔室中放入3块吸波材料。发射及接收天线均使用喇叭天线，将两个喇叭天线连接到矢量网络分析仪，测量4.5～8.5 GHz 范围内的S参数，选取100 个搅拌桨位置，使用式（2）对莱斯K因子进行计算。实验过程中，两天线始终保持正对，极化方向相同，实验系统示意图及照片分别如图2、图3所示。

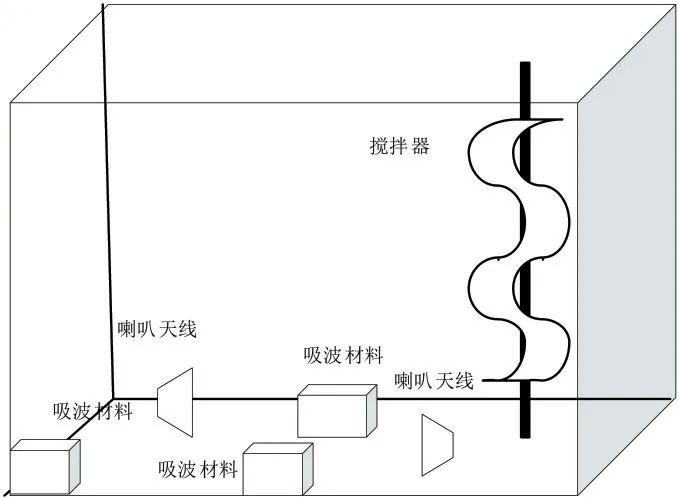
图2 实验系统示意图

图3 实验系统照片

改变收发天线间距离，对距离为0.2 m、0.4 m、…、2.0 m时的莱斯K因子进行测量计算。测量结果如图4 所示，其中，图4（a）、图4（b）分别为较短距离（0.2～1.0 m）及较长距离（1.2～2.0 m）处的K因子随频率变化的曲线。

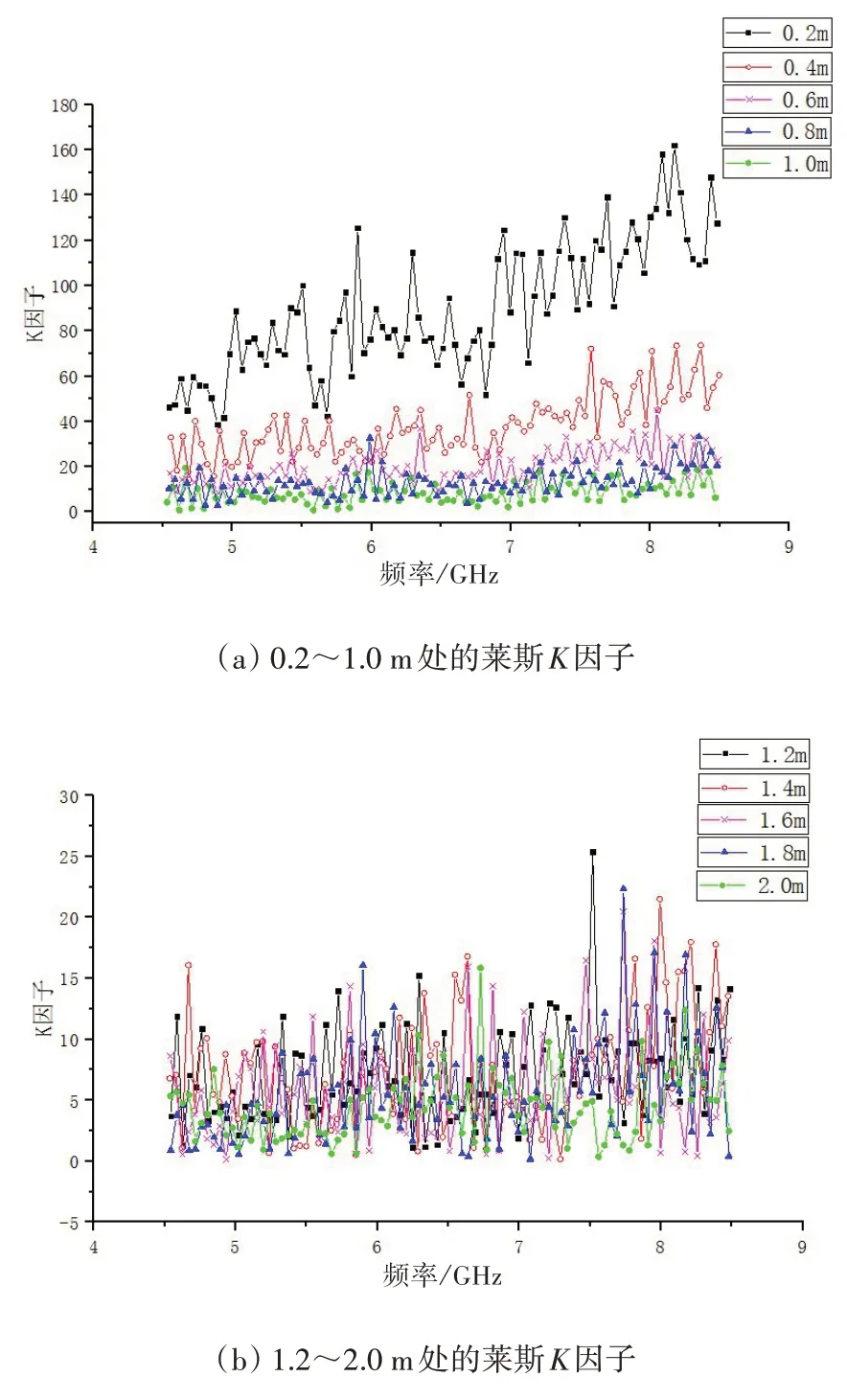
图4 0.2～2.0 m处的莱斯K因子

由图4可以看出，随着收发天线间距离的增大，莱斯K因子的值逐渐减小。当频率从4.5 GHz上升到9.5 GHz 时，莱斯K因子的数值也随之上升。与文献［2］的结论一致。

3 莱斯K因子拟合及预测

3.1 莱斯K因子拟合

为了减小测量不确定度对结果的影响，本文在机械搅拌的同时加入了频率搅拌，研究表明，当扫频带宽∆f与中心频率f的比值等于3%时，使用少量的搅拌器位置和少量的独立频率就可获得较高的估计精度［3］。因此，本文使用=3%的扫频带宽，100 个搅拌器位置对莱斯K因子进行测量计算。将5 GHz、6 GHz、7 GHz、8 GHz 频率处的莱斯K因子在0.2～2.0 m 范围内的测量结果使用Matlab 进行拟合。文献［2］将Dt、Dr假设为Dt(θ,φ)、Dr(θ,φ)，即远场方向性，因此使用式（1），即（r为收发天线间的距离,a1为参数）对天线近场处的莱斯K因子进行拟合可能存在较大的误差。鉴于此，本文除K=外，还使用了对表达式（1）进行适当修正的函数进行拟合。拟合函数如表1所示。其中，函数2、函数3 对函数1（未修正函数）的分子进行了修正。在近场处，天线的方向性随距离变化，且本文中两天线始终保持正对，即θ、φ保持不变，因此假设收发天线方向性分别为Dt(r)、Dr(r)。由于天线近场方向性的表达式较为繁琐，因此，在函数2、函数3 中分别将天线方向性简单地设为距离的一次及二次多项式。此外，函数4 对函数1 的分母进行了修正，在分母中增加了距离的一次项及常数项。表2以(a1,a2,a3)的形式展示了使用Matlab 拟合后各函数的参数取值，其中，a1、a2,、a3为函数参数。四个函数在0.2～2.0 m范围内不同频点处的拟合结果如图5所示。

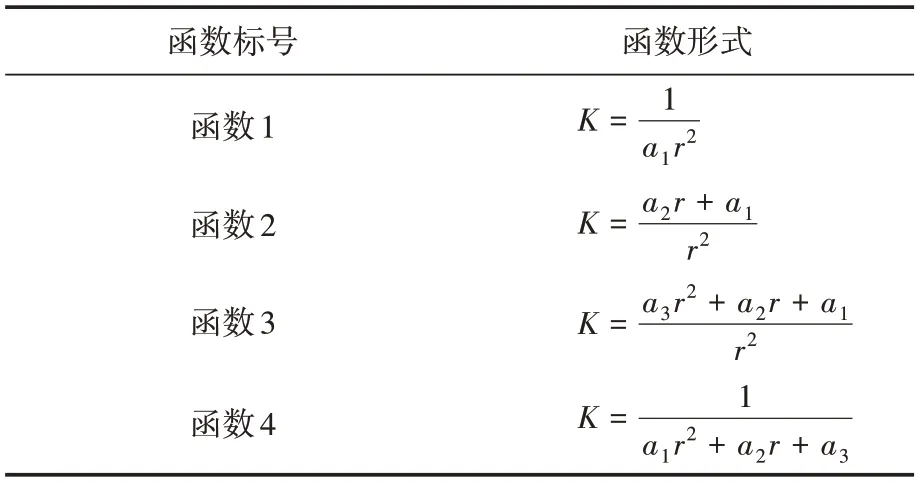
表1 拟合函数

表2 各函数在不同频率点处的参数取值

观察图5 可以发现，在小于0.3 m 时四个拟合函数之间的差距较小，四条拟合曲线几乎重叠，当距离逐渐增大时，四条曲线间的差距逐渐增大。与函数1 相比，函数2、函数4 与实测点间的差距较小，初步判断函数2 和函数4 的拟合效果较好。

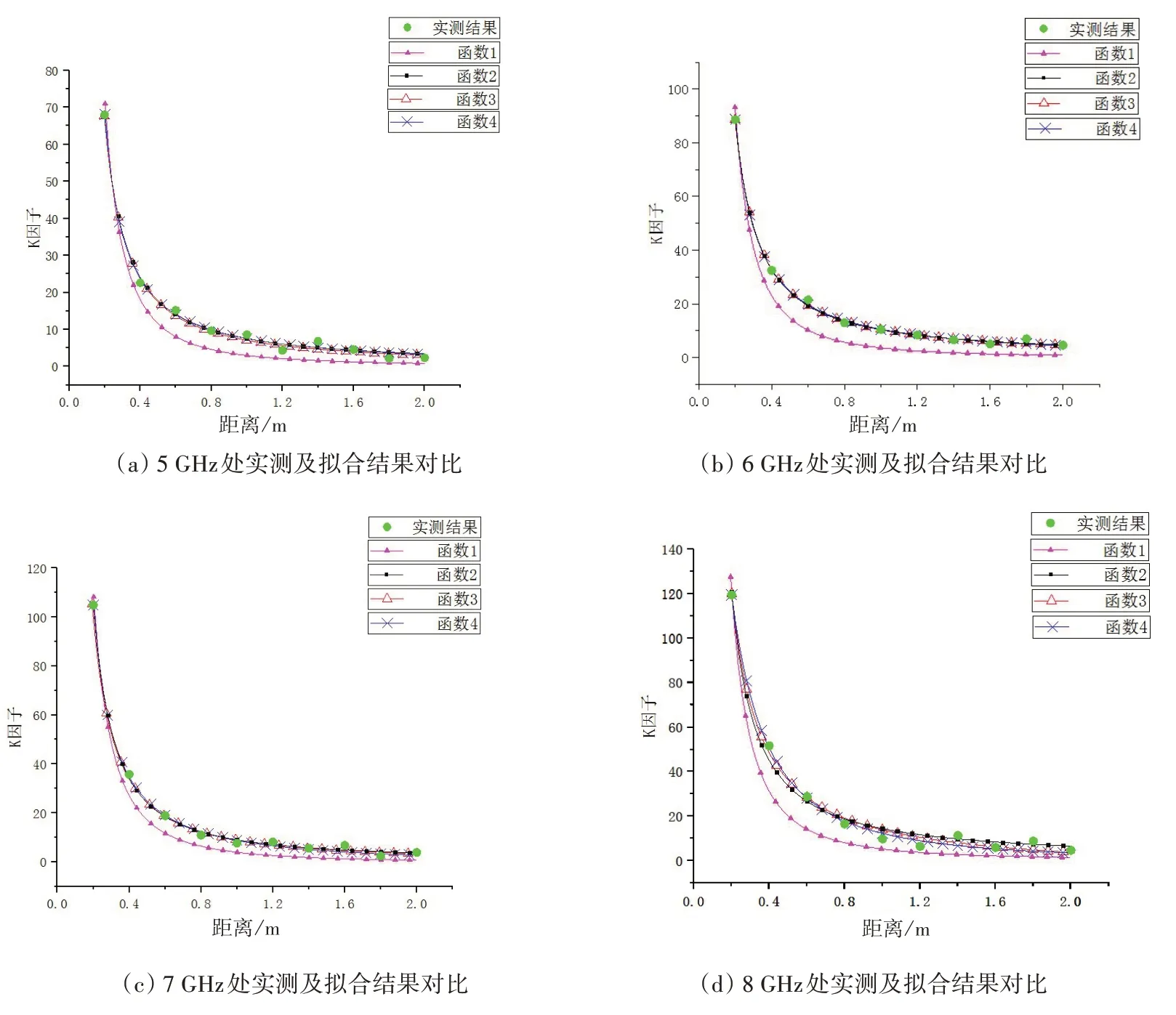
图5 莱斯K因子实测及拟合结果对比

3.2 莱斯K因子预测

本文对拟合结果使用均方根误差进行检验［7］，其公式如式（3）所示。E表示均方根误差，(xi,yi)为实测数据，f(x)为拟合函数，δi为拟合函数f(x)在xi处的误差，n为实测数据个数。将拟合函数在0.3 m、0.5 m、…、1.5 m 处的预测结果与测量结果进行对比，进一步检验拟合效果。拟合误差和预测误差分别见表3 和表4，图6 直观反映了四个函数的预测效果。

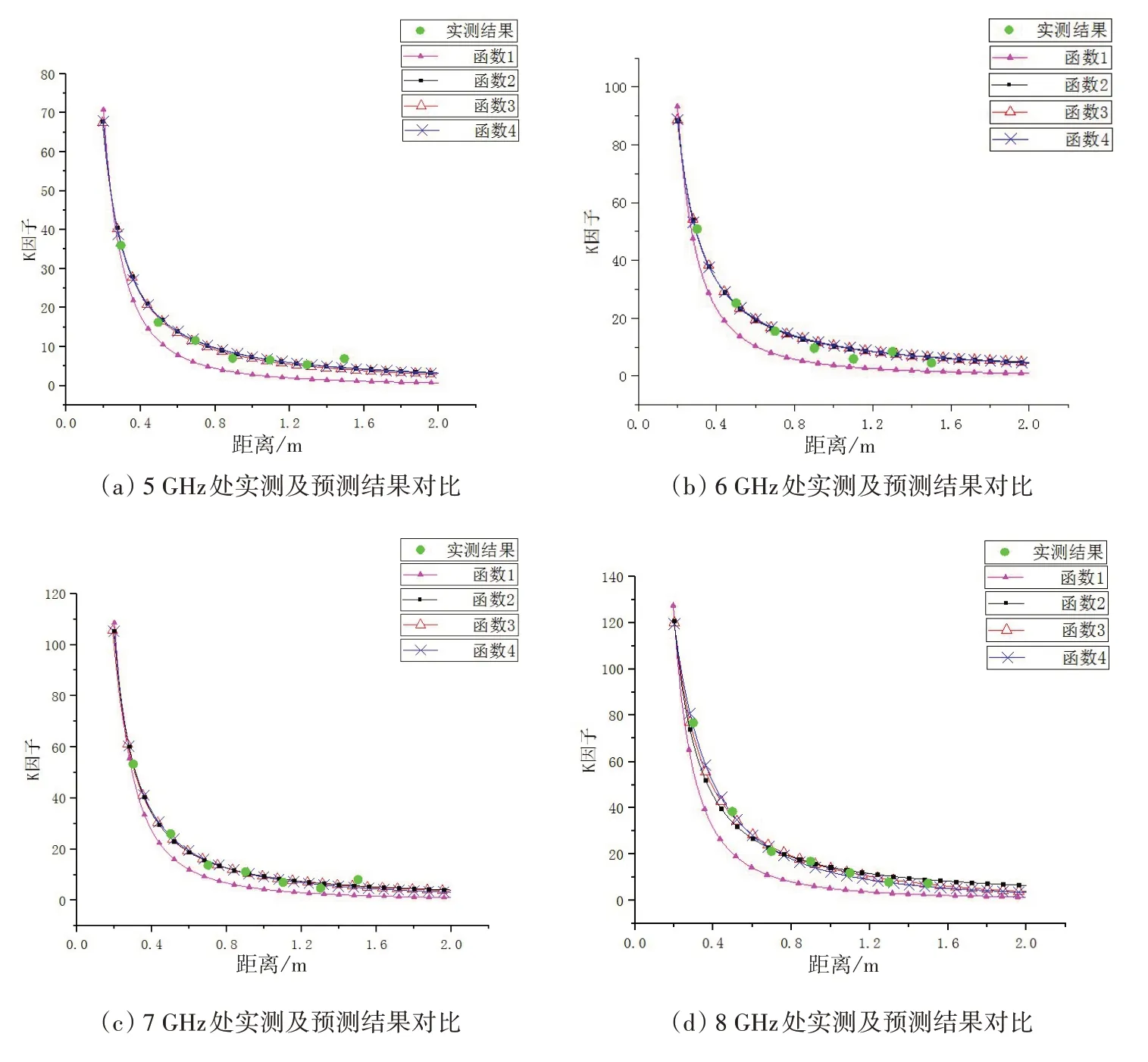
图6 莱斯K因子实测及预测结果对比

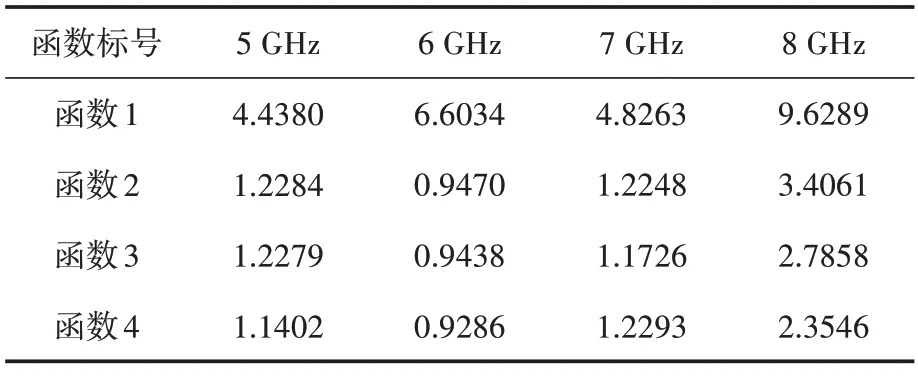
表3 拟合误差

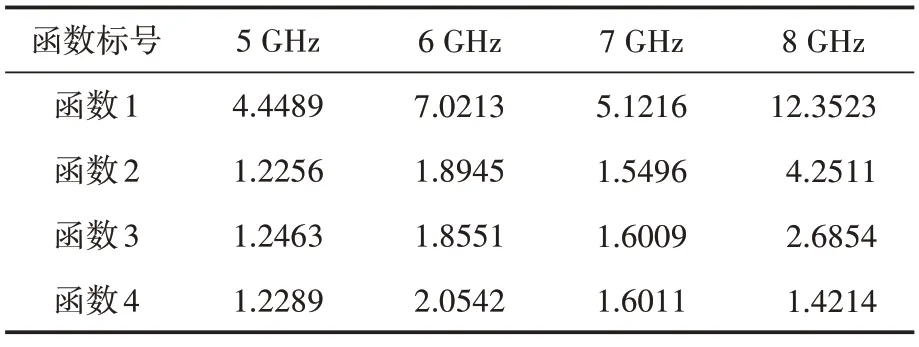
表4 预测误差

图6中，预测点的实测结果皆落在拟合曲线附近，初步判断拟合曲线预测较准。

观察表3和表4可以发现，函数1在各频点处的拟合误差及预测误差均较大，函数2～函数4的拟合误差及预测误差均较小。其中，在5 GHz、6 GHz及8 GHz处函数4的拟合误差最小，7 GHz处函数3的拟合误差最小，该三个函数在同一频点处拟合的准确度的差距很小。在表4中，5 GHz、7 GHz处函数2的预测误差最小，6 GHz处函数3的预测误差最小，8 GHz 处函数4 的预测效果最好，且除8 GHz 外其它频点处三个函数的预测准确度差距较小。因此，函数2～函数4 对莱斯K因子关于距离r的拟合较函数1更为准确。

从函数形式上看，函数1、函数2 的形式较简单，函数3、函数4 的形式较复杂。从物理意义角度分析，函数4 对函数1 的分母进行了适当修正，在分母中增加了距离的一次项及常数项，使莱斯K因子随距离的二次项及一次项变化，函数2、函数3 对函数1 的分子进行了修正，将表达式（1）中的天线方向性简单地设为距离的一次及二次多项式，它们不仅保留了表达式（1）的物理意义，还将其进行了拓展，使其在近场及远场情况下均适用。

因此，使用对Holloway 表达式进行适当修正后的函数进行拟合更为合适，根据拟合精度、函数形式或物理意义等方面的需求可选择相应的函数进行拟合，通过此拟合曲线，不仅可以预测本混响室在0.2～2.0 m之间任意距离处的莱斯K因子，还可根据所需的莱斯K因子确定其所对应的收发天线间距离，从而对具有此莱斯K因子的无线信道在混响室中进行重建。

4 结语

本文针对混响室莱斯K因子预测及信道重建的问题提出了将少量不同配置下的莱斯K因子测量数据进行拟合的方法，并以不同收发天线间距离处的莱斯K因子值的预测及信道重建问题为例进行了研究，对不同函数的拟合效果进行了比较。拟合结果表明，将Holloway 表达式进行适当修正后的函数拟合效果更优，并同时保留了Holloway 表达式的物理意义，对其进行了适当拓展。通过该方法不仅可预测不同距离处的莱斯K因子数值，还为如何配置混响室使其具有给定的莱斯K因子提供了指引。此方法对于如混响室品质因数等其它因素在不同取值处的混响室莱斯K因子预测及信道重建问题也具有普适性。此外，当研究者需要获取大量不同配置下的混响室莱斯K因子数值时，采用本方法还可减少实验次数，节省人力物力，降低测量工作量。