一种自适应无人机集群网络恢复方法

石运阳，华 翔，张金金

（西安工业大学电子信息工程学院，西安 710021）

0 引言

无人机集群是由多架无人机组成的一个完整的有机系统，集群内部的无人机通过无线自组织网络建立连接，构建成一个整体的作战单元，从而具备在复杂多变环境中执行危险任务的能力。无人机集群在执行任务过程中，无人机个体的移动会导致网络中的链路频繁改变，恶劣环境的影响也会使得部分节点失效［1］，这些都会导致集群网络的间歇连接和动态拓扑，使得网络结构受损，降低无人机集群网络的连通性能，影响集群的正常通信［2］。因此，无人机集群网络的拓扑修复应当是在网络出现结构性损伤后，自适应调整局部节点之间的链路，以保证网络整体的连通性。

目前，通信节点自适应进行链路重选的方法主要有两种，分别是基于网络结构特征的链路重选机制以及基于网络负载程度的链路重选机制。

基于网络结构特征的链路重选机制是利用几何方法对集群网络拓扑结构进行分析。马学森等［3］针对无线自组网最优传输路径问题，提出基于蚁群算法的路径寻优和恢复算法，该算法有效降低了节点的能量消耗，在出现节点死亡时可以对最优路径进行快速恢复。姚玉坤等［4］针对自组网网关节点失效问题，通过马尔可夫链路状态预测模型，提出了基于无人机-地面控制站链路状态预测的网关选择算法。李玉龙等［5］针对贪婪路由协议不能准确反映节点位置的问题，提出了一种基于移动预测和链路保持时间的路由协议MP‑GPSR，综合考虑节点的移动位置和链路保持时间来选择下一跳，避绕路由空洞，降低了传统边界转发的路径冗余。

基于网络负载的链路重选机制是确保无人机节点能有效传输其负载对象。对于随机路径移动模型，康巧琴等［6］提出了基于效用值转发的路由快速恢复算法。综合利用网络时延、节点效用值和下一跳数三个指标得到最优的下一跳节点。该算法平均跳数少、成功概率高、平均时延低。肖军弼等［7］将SDN 网络架构引入故障恢复策略，根据域间域内跳数、带宽总量、已使用的链路带宽进行通信代价权值评价，生成域间相交最小的备用路径。孙明杰等［8］提出了基于蚁群优化的路由算法，该算法将蚁群信息素与路由算法相结合，大大减少了路由拥塞和链路断路的情况。

然而，相较于传统移动自组网，无人机集群自组织网络节点之间的相对速度更大，链路质量变化也更加频繁［9］，因此对于无人机集群网络恢复算法的设计应当着重考虑无人机的移动性和拓扑时变性。传统的网络恢复算法可以可靠地寻找下一跳备选节点，但是在无人机领域会在时效性方面存在一定的不足。因此如何设计出适用于无人机高速动态拓扑的自组织网络恢复算法是目前无人机集群网络研究领域的热点和难题。

针对以上问题，本文提出一种自适应无人机集群网络恢复算法。首先，每个无人机节点利用鲸鱼算法优化后的灰色滚动模型对节点之间的通信代价进行预测。然后，当集群中的部分节点失效后，待恢复节点通过最短路径算法和负载均衡算法根据预测结果找到节点之间的最短路径，实现集群网络的自适应损伤恢复。最后，对算法进行仿真分析，验证恢复算法的时效性、恢复后网络的有效性和抗毁性。

1 无人机集群网络拓扑映射模型

无人机集群编队在飞行过程中往往是整体朝着一个既定目标进行移动［10］。本文基于复杂网络理论对无人机集群网络进行建模，采用图论方法对其进行抽象，将无人机的节点与链路映射到复杂网络模型中，考虑了无人机之间信号的功率强度、相对速度以及节点负载度等因素，将无人机的连通性恢复问题转化为复杂网络的边重连问题。

1.1 集群网络通信代价权值指标

考虑无人机集群网络拓扑时变的特点，结合无人机节点属性参量因子，由单位时间内无人机之间的通信关系建立无人机集群通信网络结构模型。将整个无人机通信网络抽象为图G(V,E,W)，其中，V(G)表示所有节点的集合，E(G)表示所有边的集合，|V|代表节点的个数，|E|表示通信链路的数量，根据单位时间内无人机之间的通信拓扑结构，可以将无人机的链路映射到图G中的连边e(i,j)。W表示无人机之间通信代价的权重矩阵，wij表示无人机编号i和j的通信代价权值指标，通过归一化后的信号稳定性指标以及链路负载度指标参数确定。

信号稳定性与节点之间的功率强度和相对速度有关。功率强度指标主要通过无人机相互之间Hello消息的信号强度确定。对于节点i，定义其接收到节点j的信号功率大小为Pij，根据自由空间传播模型，节点间功率强度计算方法为

式中：Ps为无人机节点的额定天线功率；Gs、Gr为无人机天线的接收增益参数和发射增益参数；L为信道传输路径损耗的参数；λ为波长，以上变量均为定值。

无人机之间的相对速度可以根据多普勒效应计算得到。设f为无人机节点发射功率的原频率，f′为节点j接收到节点i的载波频率，可知由多普勒效应，无论节点j相对于节点i远离或是接近，节点i和j的相对速度为

结合余弦定理和公式（1）中的自由空间传播模型，利用节点之间的功率强度对公式（2）中的三角函数进行替换，可以推导出节点i和j的相对速度：

根据公式（1）和公式（3）分别得到节点i和j的功率强度和相对速度后，两个节点之间的信号稳定度LSij就可以根据以下公式得到：

式中：i与j是对应链路两端的发送节点和接收节点。Pij是节点i和j间的信号功率强度，vij是节点i和j的相对移动速度，Ps和vmax分别表示无人机的发射功率与节点最大速度。λ和φ分别为功率和速度的权重因子，且λ+φ=1。

Pth为设定的对应链路最小阈值，其对应于处在无人机通信边缘且相对距离恰好为最大通信半径减去通信时延tde_min的邻居节点。设置链路最小阈值可以避免节点选择生存时间非常短的链路。

链路负载度指标映射到边权重时，定义为两端节点的负载均值：

通信代价权值代表两架无人机之间通信困难程度，相对移动速度越快、信号强度越小、链路负载程度越高，无人机之间的通信代价就越大。根据公式（4）和公式（6），信号稳定性越大、链路负载越小，通信代价越小，因此定义通信代价权值wij为链路负载度指标与信号稳定性指标的比值：

其中：kLC和kLS分别为链路负载度指标和信号稳定性指标的权值。可以看出，当信号稳定性越高、节点负载度越小时，节点i与j之间的通信代价越小；当节点信号强度低于阈值强度后，通信代价为无限大。

1.2 无人机集群初始网络拓扑结构

无人机集群系统一般采取密集编队模式，每个通信个体与最近几个邻居进行通信。考虑一个包含n架无人机的无人机集群，假设所有的无人机具有相同的结构和运动能力，无人机的通信半径为Rm。设定无人机集群中包含一架领航无人机以及n-1 架跟随无人机，运动方式为参考群组移动模型。领航无人机在接收到上位机的命令后，会沿着任务信息所规划的航迹进行飞行，跟随无人机根据邻居节点自动调整位置，保证每个无人机的运动轨迹与集群整体一致，因此领航无人机无需与集群中所有无人机实时进行数据同步，任意一个无人机都可以成为领航节点，每个无人机只需要与邻居无人机保持相似的运动轨迹，即可实现集群运动的同步。

设定无人机集群整体以速度v0朝着一个既定目标飞行，在飞行过程中，由于自然因素和无人机自身性能因素，每架无人机速度会在一定范围内波动，定义无人机i在时刻t的速度为vi(t)，在网络拓扑模型G(V,E,W)中，任意节点i的速度为

每个无人机在速度偏离整体速度后都会自适应进行速度调节，因此在所有时间的速度收敛于v0，可以用以下公式进行描述：

无人机集群运动状态如图2 所示，选定16号节点为领航节点，在图中用黄色标出，其余蓝色节点为跟随节点。考虑到节点之间的通信链路为双向链路，因此集群网络拓扑结构应当具有对称性，网络所映射的图论模型也应当为无向权重图。无人机与其最近的几个邻居节点建立双向链路，构成如图2所示的网络拓扑。

图2 无人机集群运动方式与初始网络拓扑

在无人机集群执行任务过程中，当无人机集群中节点数较多时，节点因发生故障而出现失效的情况在所难免。此时，网络拓扑会因该节点的移除而发生改变，进而影响整个网络的连通性。如图3（a）所示，如果14号和28号节点发生故障，无人机集群网络映射到图论中的数学模型则转化为图3（b）。在图3（b）中，无人机集群网络内部虽然能够进行信息交互，但是22号节点承担了右下方通信子集与其他节点之间的通信，如果22 号节点发生故障，则无人机集群网络被分割为两个不连通的子集，此时，集群内部节点无法进行信息同步，集群整体的网络性能发生了严重的下降。因此，本文从节点移除对网络连通性造成的影响角度来考虑无人机飞行自组织网络的连通性维护问题，通过链路预测算法与局部拓扑修复算法，实现网络的连通性恢复。

图3 节点发生故障后网络拓扑变化图

2 网络修复算法

灰色预测是一种能够针对样本数据量小、数据变化不规律的时间序列进行预测的方法，具有预测速度快、预测拟合度高、参数估计简单和预测结果可检验等优点。本文采用灰色滚动预测算法，对节点之间的链路状态信息进行实时预测。但由于灰色预测算法在非线性数据序列预测方面存在准确性不足的问题，因此本文利用鲸鱼优化算法，考虑了“新信息优先”原则，对灰色预测算法时间响应函数的初始值进行改进，提出了鲸鱼权值优化-灰色滚动（whale optimization algorithm‑weight of grey model，WOA‑WGM）预测算法。

相较于传统的灰色预测算法，本文提出的鲸鱼权值优化-灰色滚动预测算法有效提高了预测的精确度，增加了预测值与样本数据序列之间的关联性，并具有良好的非线性时间序列预测能力。此外，通过Dijkstra 算法对局部拓扑恢复路径进行寻优，考虑链路负载方差，并通过鲸鱼算法对寻优后的路径进行负载均衡处理，实现局部拓扑的最优恢复，提高恢复后网络的鲁棒性。

2.1 灰色滚动预测模型

GM（1,1）灰色预测是一种可以对不确定时间序列进行拟合和估计的有效工具，其数据样本空间允许少到4个，非常适合于链路质量的快速估计［11］。无人机集群网络拓扑结构变化频繁，需要及时对下一时刻的链路状态进行预测，因此在灰色预测模型中加入时间窗口，不断去旧值、添新值，保证样本数据的实时性。

设原始时间序列为W(0)={w(0)(1),w(0)(2),…,w(0)(n) }其中w(0)(k)是在时刻k时的数据。w(0)的累加生成序列为W(1)={w(1)(1),w(1)(2),…,w(1)(n) },其中对于GM（1,1）预测模型，其灰色微分方程为

式中，z(1)(k)=0.5w(1)(k)+0.5w(1)(k-1),k=2,3,…,n；a和b分别为发展系数和灰作用量。将时间序列W(0),W(1)代入公式（10），可以得到如下公式：

将公式（11）转化为矩阵形式，即可得到：

求解上述公式，可以得到参数a和b的最小二乘估计：[a,b]T=(BTB)-1BTY。

对输入的时间序列建立用于预测的微分方程：

将参数a和b的预测值代入公式（13），并将w(1)(1)=w(0)(1)作为初始条件代入，得到公式（13）求解后的时间响应函数：

由此，即可得到k+1时刻的链路稳定性预测值。

2.2 鲸鱼权值优化模型

2.2.1 时间响应函数优化策略

经典灰色预测的时间响应函数的初始条件为输入时间序列的第一个参数，当进行滚动预测时，会导致对信息的适应能力下降，从而导致灰色预测模型的预测性能降低。针对这个问题，本文通过对时间响应函数的初始序列进行加权处理，利用鲸鱼算法在每次滚动预测时对权值进行寻优。经典灰色预测时间响应初始条件为w(0)(1)，本文设定新的时间响应函数初始条件为w(1)(β)，对其进行加权处理，具体为

优化后的时间响应函数为

其中：αn-k(0 <α<1)(k=1,2,…,n)是动态权重系数，β(1 ≤β≤n)是时间输入系数。

新提出的初始条件也充分考虑了影响模型准确性的历史信息，由于α满足0<α<1，因此参数α次数越高，权重越小，即k值越大，相应的x(1)(k)加权值越大：

生成系数α和β的最佳值是通过最小化预测值和实际值之间的平均绝对百分比误差来计算。为此，优化初始条件下的最佳生成系数由以下目标函数确定：

2.2.2 鲸鱼算法权值寻优

逼近目标函数的最小值有助于获得权重系数的最优值。由于目标函数的非线性特性，无法采用常规方法求解，而智能优化算法可以简单、快速地解决非线性优化问题。其中，鲸鱼算法收敛速度快、局部搜索能力强，可以快速得到近似最优解，因此，本文采用鲸鱼优化算法对模型参数进行优化，使得该模型的建模误差减小，进而获得模型非线性参数的最优值。

鲸鱼算法是通过模拟鲸鱼捕获猎物的方式来实现寻优，鲸鱼算法求解过程主要经历三个阶段：搜寻猎物阶段、环绕包围以及起泡网狩猎［12］。鲸鱼算法位置更新方式中，环绕包围捕猎和螺旋式路径捕猎概率p等同，因此位置更新公式为

式中，T表示最大迭代次数。

在利用鲸鱼算法对参数进行权值寻优之前，首先需要设定待求参数α和β的上界和下界，并对算法参数进行初始化，然后生成初始鲸鱼位置序列，通过三种策略迭代更新鲸鱼个体适应度最高的位置，最后，达到最大迭代次数，输出最优解。具体步骤如下：

第一步：初始化鲸鱼算法的参数r,p,l,b，设置鲸鱼算法的种群数量N、最大迭代次数T，确定算法的复杂度；

第二步：初始化鲸鱼种群位置X={x1,x2,…,xN}，并设置待求参数α和β的范围区间。其中，权重参数α的范围为α∈(0,1)，时间输入系数β的范围为β∈[1,n]；

第三步：根据算法的成本函数计算鲸鱼个体的成本值，选择成本值最低的鲸鱼个体作为最优解，鲸鱼优化算法的成本函数如下：

第四步：更新鲸鱼优化算法的参数；

第五步：根据公式（19）对鲸鱼个体位置进行更新。鲸鱼个体位置更新分为三种：搜寻猎物阶段、环绕包围以及起泡网狩猎。根据更新的参数选择相应的方法进行位置更新，并对鲸鱼个体的成本值进行计算，更新最优解；

第六步：判断算法是否达到最大迭代次数，若未达到，则转第三步，否则输出最优解作为参数α和β的最优值。

利用鲸鱼算法找到最优解后，即可确定初始条件的权重参数和时间参数的最优值，将其代入灰色预测算法，对输入序列进行预测。在滚动预测过程中，需要不断对输入序列去旧值、添新值，并在每次滚动预测过程中，利用鲸鱼优化算法对新的初始条件进行优化，保证数据预测的准确性。预测算法全部过程如下：

第一步：采用实际观测值w(0)(1),w(0)(2),…,w(0)(c)作为灰色滚动预测算法的输入数据。根据上述成本函数，使用鲸鱼优化算法计算参数α和β。由此可以获得预测数据

第三步：重复上述步骤，直到预测出所有剩余数据点。

2.3 Dijkstra和鲸鱼优化网络拓扑修复算法

本文设计的网络拓扑恢复算法将网络结构和网络负载都纳入考量。针对网络结构，通过预测后的通信代价矩阵，选择通信代价最小的链路进行重建，这样有助于网络整体的可靠性。但是，仅考虑通信代价进行拓扑修复可能会导致少量链路的负载过大，从而引起整个网络的传输性能下降，因此网络恢复算法应当能够在最小通信代价的基础上对拓扑进行负载均衡处理，优化集群网络内部的链路数量于链路负载，保证集群内部信息能够进行有效传输的同时对拓扑结构进行改善。考虑到无人机移动速度快、通信链路质量变化频繁的特点，对局部拓扑恢复寻优的问题很难采用某种解析方法去解决，而鲸鱼算法可以在有限计算时间内寻找优化问题的最优解或者次优解，因此本文提出将Dijks‑tra 算法［13］和鲸鱼优化算法相结合，来对网络拓扑进行修复。

使用本文预测算法预测得到链路权值后，需要对备选节点进行筛选，选择合适的节点建立新的链路。首先通过Dijkstra 算法寻找通信代价最小的链路，核心思想是选定一个起始节点和目的节点，其余待恢复节点为必经节点，利用基于回溯法的Dijkstra 算法寻找起始节点与目标节点之间的最佳路径。如图4所示，虚线代表预测的链路，实线双箭头代表节点之间存在双向稳定链路，在当前时刻，节点Z失效，节点X与节点Y 链路断开，对这两个节点执行网络恢复策略。

图4 无人机节点链路重选示意图

根据公式（6）可知：通信代价越高，节点之间的相对速度和距离就越大，因此取通信代价最小的路径作为最优恢复路径。设节点X 到节点Y 的路径边集为EXY，则X 到Y 的最小通信代价路径为

由公式（9）可以计算无人机链路负载权值，要实现无人机恢复后的局部拓扑负载优化，本文通过计算恢复后拓扑负载的方差来衡量链路负载均匀度：

其中：LCe代表局部拓扑中无人机链路e的负载权值；N代表无人机局部拓扑的链路数目；AVG代表局部拓扑的负载权值均值，由以下公式确定：

综合考虑无人机的通信代价E和链路负载均匀度D，对于局部拓扑Gpart，将以无人机网络中的通信代价E和负载均匀度D作为目标函数，通过权重k来均衡无人机，使得在架构成本和负载均衡之间做出权衡，最终设计方案应使得目标函数尽可能小，即拓扑设计方案的成本更低，负载更均衡：

根据无人机拓扑恢复的目标函数，结合无人机网络中对于链路的相关约束，可以得到以下无人机拓扑恢复方法的目标函数：

将上述优化目标函数代入到鲸鱼算法中进行寻优，设置鲸鱼算法的成本函数为

根据算法的成本函数，计算鲸鱼个体的成本值，以成本值最低的鲸鱼个体作为当前的最优解，并通过收缩包围、螺旋运动和随机游走三种方式，对鲸鱼算法的参数选择相应的方法进行位置更新，并对鲸鱼个体的成本值进行计算，更新最优解，最终实现对无人机局部的拓扑恢复。

3 实验结果与仿真分析

3.1 实验参数设置

本实验通过Python 仿真平台进行算法的仿真，并对本文提出的WOA‑WGM 预测算法进行仿真分析，以验证不同网络损伤类型下集群网络的生存能力和抗毁能力。具体的仿真参数设置如表1所示。

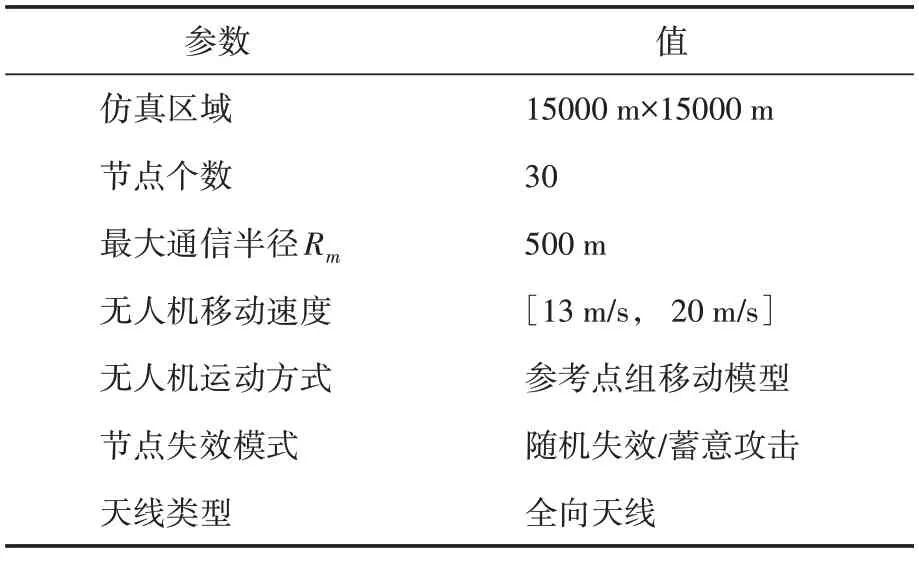
表1 仿真参数设置

为了对本文提出的网络恢复算法进行仿真评估，本文选取BA 无标度网络算法以及LPN（link prediction based on neighbors）一跳邻居链路预测算法这两个经典恢复算法对比分析网络恢复性能。在BA 网络修复算法中，需要进行连通性修复的节点会自发寻找通信范围内重要度最高的节点进行边重连，修复后的网络具备一定的无标度网络特性。LPN 网络算法会对每个节点的通信代价矩阵［9］进行预测，根据预测结果，选择链路权值最好的节点进行重连，实现网络的连通性恢复。在仿真实验中，首先分析本文网络恢复算法在集群最大速度不同的情况下恢复网络连通性所用的时间，验证本文算法的时效性；其次，验证无人机集群网络在随机失效下的网络恢复能力，验证算法恢复后网络的生存性；最后，评估蓄意攻击下无人机集群网络的恢复能力，验证恢复后网络的抗毁性。

3.2 仿真实例分析

根据以上介绍的仿真环境及参数设置，对无人机集群整体位置进行仿真模拟，每个无人机参考领航节点，以速度v0+vrand在区域内部进行飞行。每个无人机与自身若干相邻节点建立链路，组成网络的初始拓扑结构。在进行了13次飞行仿真后，得到如图5所示的网络拓扑结构。

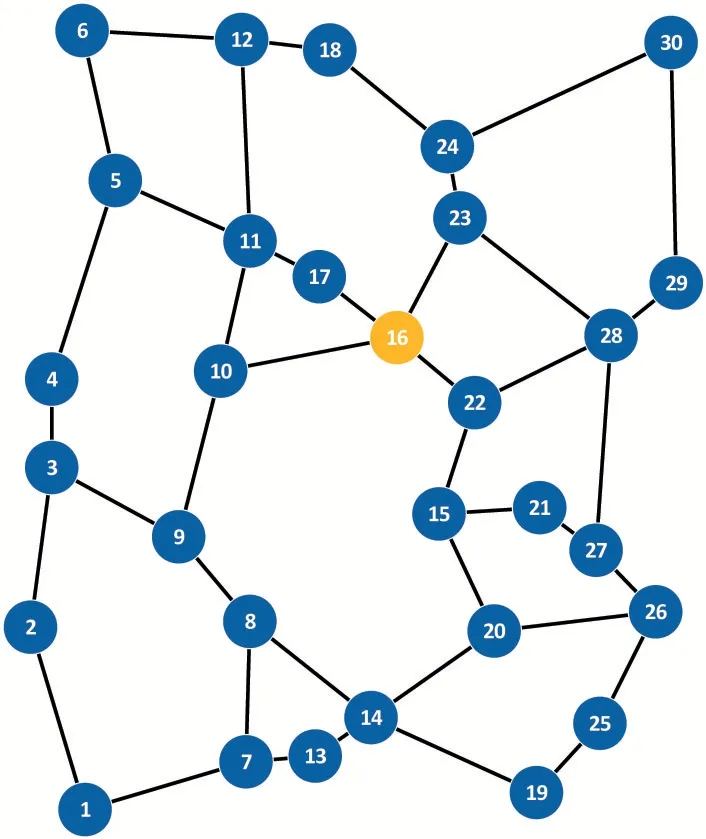
图5 无人机集群网络拓扑结构

在13 次仿真过程中，每个无人机通过与邻居节点进行信息共享，根据自身与邻居节点的信号功率强度、相对速度和负载程度计算出对应的通信代价权值wij。集群中的无人机根据权值生成集群网络的通信代价矩阵W，以预测窗口大小为基准代入多个时刻的历史样本数据，通过WOA‑WGM 算法预测得出通信代价的预测矩阵,如图6所示。

图6 通信代价预测矩阵

其中：A1,A2,…,A30代表无人机节点编号，inf代表无人机节点之间不存在通信链路。

采用表1的参数进行仿真实验，随机产生失效节点ID。设集群网络中的失效节点集合为FN，则集群网络中拓扑结构受到影响的无人机节点向其邻居节点发送网络恢复请求，集群内部通过信息共享得到待修复节点集合RN。集合FN和RN包含的节点如下所示：

节点编号为14、22、28 的无人机失效后，集群网络拓扑结构如图7所示。在图中，绿色节点代表连通性受影响节点集合RN，红色节点代表失效节点集合FN，阴影部分表示需要对该部分的局部拓扑结构进行修复。

当节点A14,A22,A28失效后，集合RN中的节点按序依次寻找最短路径。集合中的待恢复节点根据通信代价矩阵预测值,通过最小通信代价路径算法遍历出待恢复节点之间的路径，以此实现网络局部拓扑结构的修复，结果如表2所示，通过最小通信代价修复后的拓扑图如图8所示，通过修复算法找到节点之间的最小通信代价路径用点线表示。

表2 节点之间最短路径表

图8 最短路径拓扑修复图

利用最小通信代价算法进行了初步修复后，需要继续对其进行负载优化。在实验中，假设每个无人机都向邻居节点发送长度为1 帧的数据，长度为256 byte，周期为4 ms。经过仿真实验，比较了直接寻找最小通信代价方案和优化设计方案，得到了链路数、负载均值和负载方差的对比数据，如表3 所示。拓扑修复图如图9所示，图中待修复节点根据最短路径对局部拓扑结构进行修复，避免因节点失效造成网络整体重新进行拓扑重构。同时，本文算法提出的网络修复方案在链路数量上进行了一定的优化，网络体系代价有了明显的降低，负载更加均匀，提高了集群网络的鲁棒性和健壮性。

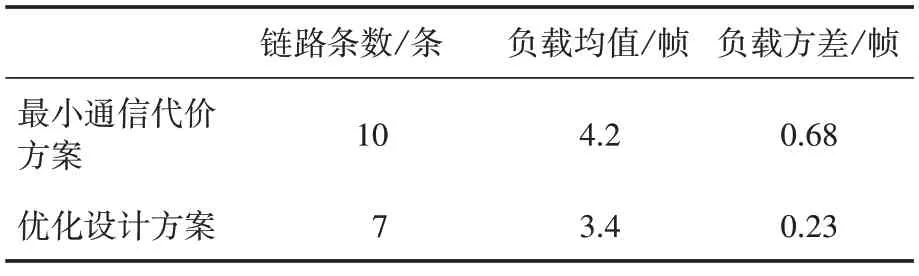
表3 仿真对比结果

图9 WOA⁃WGM 实现无人机集群网络拓扑修复

3.3 网络恢复时效性分析

网络恢复时效性分析是指在无人机集群网络受到损伤后，恢复网络的连通性所需要的时间。图10中分别表示了不同速度与损伤情况下，本文算法与BA 算法和LPN 算法恢复网络的时效性对比，为消除可能存在的随机误差，采集的实验数据均为进行10次仿真后求得的平均值。

图10 无人机集群网络恢复算法时效性对比

在图10（a）中，设定无人机集群在3 个节点失效的情况下，不同算法在不同的速度恢复网络连通性所需的时间，可以看出，在无人机集群最大速度小于10 m/s 时，经典BA 算法和LPN算法由于其计算复杂度低，可以很快找到合适的链路进行拓扑修复。而随着无人机的最大移动速度增大，三种恢复算法耗时均存在不同程度的增加，BA 算法和LPN 算法增加最为明显，这是因为随着无人机移动速度的增加，节点之间的信号强度和相对速度变化越频繁，BA 算法由于没有预测机制，在恢复网络连通性时需要不断试错，LPN 算法虽然可以对邻居节点的链路进行预测，但是预测结果精确度不足，且不能对多跳链路进行预测，难以实现整个集群网络的连通性恢复。在图10（b）中，设定无人机集群在15 m/s 的最大速度下，不同算法在损失不同数量的节点修复网络拓扑所需的时间，同样，经典BA 算法和LPN 算法都随着失效规模的增大，恢复耗时急剧增加，而本文算法由于加入了改进的预测机制和多节点路径恢复机制，对下一时刻的无人机速度和链路距离进行了预判，对于速度的变化较为敏感，能够使无人机在高速移动时选择到高稳定链路，从而减少了不必要的路由开销，实现网络连通性的快速恢复。

3.4 网络恢复生存性分析

网络恢复生存性是指无人机集群网络恢复算法在节点随机失效情况下，恢复网络连通性的能力。本文通过网络最大连通度和平均路径长度比例对网络性能进行分析［14］。

网络最大连通度G表示最大连通子图节点数占总节点数的比例，表达式为

对于带权无向图，平均路径长度与边权值相关，平均路径长度L表达式如下：

则平均路径长度比例L*为受到影响后集群平均路径长度与初始平均路径长度的比值：

在仿真实验中，随机选择集群中的无人机失效，分析无人机集群在不同失效规模下使用不同算法恢复后网络的生存性。结果如图11 所示。图11（a）为网络最大连通度随失效规模变化的曲线，可以看出，在失效比例小于0.4 时，BA 算法集群内部的最大连通度要高于LPN 算法，这是由于BA 恢复算法选取度值最大节点实现边重连，恢复后的网络相较于LPN 算法能够更好地保证网络整体连通性。LPN 算法由于优先选取通信代价最小的链路实现边重连，因此容易陷入局部最优而忽略集群整体的连通性能，导致集群内部被分割为多个不连通的子集，降低网络的连通性。而本文算法考虑了所有网络拓扑受到影响的节点之间的连通性恢复，因此在网络拓扑连通性恢复过程中，节点在失效比例小于0.5 时，能够一直保持集群内部的连通性不受影响，即使在网络大规模失效，本文算法在网络整体的连通性能恢复上也更优于BA 算法和LPN算法。

图11 无人机集群网络生存性指标

图11（b）为平均路径长度比例随失效规模的变化曲线，当节点失效比例小于0.2 时，BA 网络恢复算法所平均路径长度比例优于LPN 算法，这也验证了BA 算法在执行恢复策略时，能够使得网络中连通性下降的节点自动在通信范围内选择连通度最高的节点实现网络重连，网络整体的连通性更好。然而当节点失效比例超过0.2时，BA 算法的平均路径长度比例大幅降低，可以看出，当随机失效作用到关键节点时，BA 算法所恢复的集群网络连通性会受到很大影响，网络中出现大量分割的连通子集，导致网络整体的生存性下降。本文算法相较于BA 算法和LPN 算法，平均路径长度比例下降更为平缓，在不同失效规模的情况下均优于传统的BA 算法和LPN 算法。综合最大连通度和平均路径长度比例，算法能够尽力维持网络整体的连通性，且平均路径长度比例在60%以上，此时网络处于相对可靠的状态，这是因为本文提出的算法在网络出现损伤后，会及时修复所有连通度下降节点之间的网络拓扑，补偿损失的节点连通路径。

3.5 网络恢复抗毁性分析

网络抗毁性分析是无人机集群网络在遭到恶意攻击作用下，集群内部保持连通性能的能力。在仿真实验中，通过选取无人机集群网络中节点度值较大的节点进行失效仿真，分析网络恢复算法在不同失效规模下使用不同算法恢复后网络的抗毁性。结果如图12所示。

分析图12（a）中网络最大连通度随失效规模变化的曲线，可以看出BA 算法的网络性能恢复能力是三种恢复算法中性能最差的，这是由于BA 算法恢复后的网络具有一定的无标度网络特性，在随机失效时具有良好的鲁棒性，但是对于蓄意攻击是脆弱的。LPN 算法虽然相较于BA算法在面对蓄意攻击时具有更好的恢复性能，但是网络最大连通度还是出现了大幅下降，难以维持集群整体连通性。本文算法在失效比例小于0.5 时，依然能够维持集群整体的连通性，且在失效规模继续增加时，最大连通度下降曲线较为平缓，优于传统的BA算法和LPN算法。

从图12（b）可以看出，BA 算法和LPN 算法在面对蓄意攻击时，平均路径长度比例在较小的失效规模下发生了急剧下降，网络整体已经处于多个不连通子集状态。而本文算法可以对通信代价实时预测，快速选择合适的节点建立链路，同时通过最小通信代价策略初步对缺失链路进行恢复，并通过负载均衡策略对链路进行优化，因此从图中可以看出，不同失效规模下，平均路径长度变化较为平缓，不会由于新增链路造成网络平均路径长度发生急剧变化，实现了无人机集群网络的有效恢复，减少了不必要的冗余链路，保证了网络的可靠性。

图12 无人机集群网络抗毁性指标

结合图11 和图12 中的数据，本文提出的网络恢复算法在随机失效和蓄意攻击下相较于传统的网络恢复算法能够更好地维护网络性能，并且在失效比例不超过0.5 的情况下，能够稳定地维持集群整体的连通性。在节点失效比例在0.5 至0.7 时，集群网络内部大范围节点都已失效，本文提出的算法在最大连通度和平均路径长度比例方面都明显优于BA 算法和LPN 算法，表明本文算法在集群遭到大规模损伤时仍然能够尽力维持集群中的极大连通子集，提高网络的生存性和抗毁性。

4 结语

针对高动态拓扑下无人机节点失效造成的网络性能和可靠性下降的问题，本文根据信号稳定度指标和链路负载度指标计算无人机之间的通信代价，构建无人机集群网络通信模型，并通过鲸鱼权值优化-灰色滚动链路预测算法对通信代价指标进行预测，降低了无人机高速移动对修复算法实时性的影响，最后利用最短路径算法和负载均衡算法，实现了网络连通性恢复并优化了网络恢复后的拓扑结构。实验结果表明，该方法在无人机集群网络出现节点失效时可以快速进行拓扑重构，恢复通信节点之间的链路连接，实现网络连通性恢复，并使恢复后的网络具有良好的生存性和抗毁性。