无人机遂行编队飞行中的纯方位无源定位

仵云凡 朱代根 高朋 艾慧婷 李娟

西南林业大学机械与交通学院 云南省昆明市 650224

1 引言

无人机集群在遂行编队飞行时，为避免外界干扰，应尽可能保持电磁静默，少向外发射电磁波信号。为保持编队队形，拟采用纯方位无源定位的方法调整无人机的位置，即由编队中某几架无人机发射信号、其余无人机被动接收信号，从中提取出方向信息进行定位，来调整无人机的位置。编队中每架无人机均有固定编号，且在编队中与其他无人机的相对位置关系保持不变。

假设编队由10 架无人机组成，形成圆形编队，其中9 架无人机（编号FY01～FY09）均匀分布在某一圆周上，另1 架无人机（编号FY00）位于圆心。无人机基于自身感知的高度信息，均保持在同一个高度上飞行。

2 模型假设

假设仅考虑纯方位无源定位的情形将目标视为变质量质点，不考虑绕质心的旋转方程。

卫星测量的白噪声与输入不相关。忽略目标红外信号的传播时间及卫星对红外信号的处理时间。

两颗测量卫星的时钟始终保持同步。在探测过程中，目标没有进行推进级分离或发动机停机操作。

目标飞行的轨迹在一个平面内。模型的建立与求解被动接收信号无人机的定位模型与TOA 位置相比，TDOA 位置降低了观测站和辐射源的时钟同步要求，定位系统相对稳定可靠，应用广泛。AOA 定位系统结构简单，解决方案可靠。但AOA 位置受多路径影响较大，对天线要求高，导致定位效率低。针对这一问题，结合AOA 定位进行固定辐射源跟踪，并将AOA 观测作为AA、AA 联合定位的辅助观测，提高了定位精度。在无人机对固定辐射源进行定位的研究中，它们被用作源探测手段的载体。无人机机动性强，其定位误差不容忽视。仅通过上述组合定位算法获得的定位精度有限，往往需要对辐射源进行长时间的观测。由于多架无人机的观测矢量是一种非线性辐射源定位方法，可以结合非线性滤波算法对辐射源状态参数进行滤波更新，进一步提高定位效率。

基于TDOA/AOA 联合定位方法的研究

多无人机基于TDOA/AOA 联合定位方法的流程图如图2 所示。

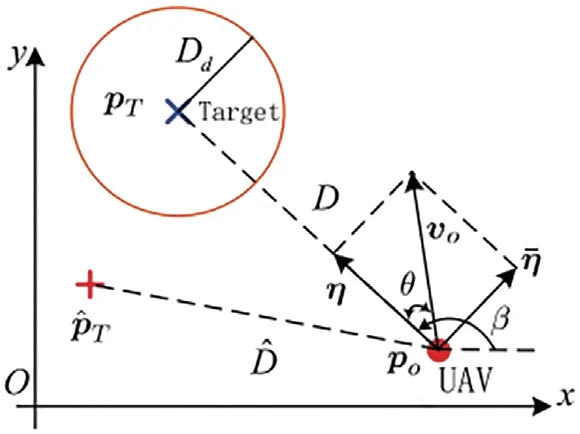
图1 飞行轨迹

由于普通的AE 网络每层都是由普通的全连接层组成，因此编码器的输出结果可表达为公式（1）所示：

其中f()· 为编码器的激活函数，Wj与bj分别代表的是本层网络的权重矩阵与偏移向量。同理，译码过程的数学表达式可以描述为公式（2）所示：

在自编码器训练当中的为了使编码器的输入数据与译码器的输出数据分布尽量相似，应使其相对误差越小越好，通常我们会使用均方误差（Mean Square Error，MSE）函数作为自编码器训练当中的损失函数，见公式（3）。除了MSE 函数之外常见的损失函数还有交叉熵损失函数、log 对数损失函数以及合页损失函数等。

然后极小化φ[Z(x)]，即求解

基于这个现实，构造如下评价函数，即

克拉美罗下界

克拉美罗下界经常用于计算理论能达到的最佳估计精度，而定位实质上就是对辐射源参数进行估计，可以将 CRLB 作为评价定位性能的指标，故本章节根据无人机是否考虑站址误差，分为以下两种情况对辐射源位置的 CRLB 进行分析。

（1）min-max 归一化

Z-score 标准化

辐射源位置的CRLB 可以通过分块矩阵求逆原理进行求解：

其数学公式如公式（13）所示：

模型应用

在时差测量误差和站址误差不变的情况下，根据角度测量误差的变化对定位性能进行分析。

由图3 可知，当无人机角度测量误差较小时，不管是否考虑站址误差，TDOA/AOA联合定位算法的定位精度要优于TDOA 定位。此外，随着AOA 测量误差的增加，TDOA/AOA 定位精度逐渐恶化。

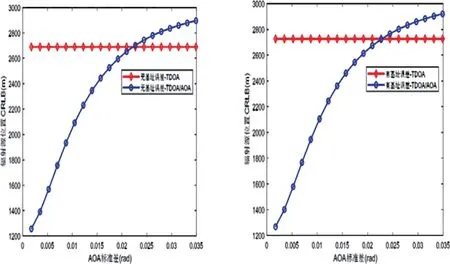
图3 不同角度测量误差情况下辐射源位置的CRLB

角度测量误差对TDOA/AOA 定位精度的影响：

由图4 可知，在时差测量误差固定的情况下，角度测量误差越小，定位精度越高；反之，定位精度越低。

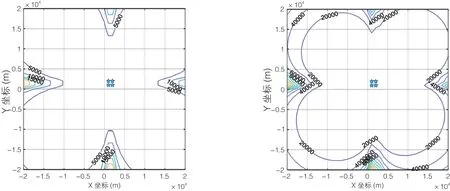
图4 不同角度测量误差情况下GDOP 等高线分布图

定位精度指标

前两部分指出辐射源定位精度与测量误差和台站定位误差有关。由于这些误差，辐射源定位结果与辐射源实际位置之间存在一定的随机误差。定位能力可以通过使结果偏离发射机的实际位置来测量。偏差越小，定位越好。在无源定位系统中，定位质量主要从两个方面进行评价。

如图5 所示，项目2.0.5s10 考虑的是车站地址误差，而不是其地址误差，这样就可以得出辐射源位置的均方根误差。辐射源位置的均方根误差小于站点位置的均方根误差，表明考虑站点地址误差的联合定位算法的定位精度有所提高。在使用由无人机控制的多个辐射载体时，应考虑站位误差。

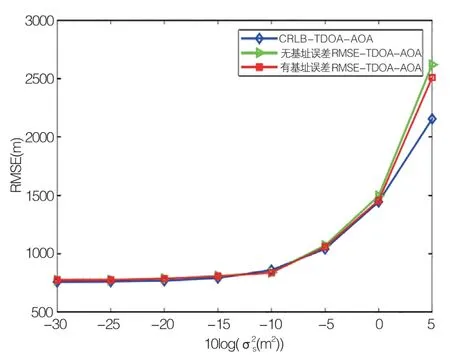
图5 不同站址误差情况下辐射源定位的均方根误差

无人机的有效定位

非线性滤波算法

卡尔曼滤波(Kalman Filter，KF)是一种线性滤波和预测方法，通过各观测站的接收参数实现对辐射源状态矢量的最优估计，可以得到较好的跟踪效果。但是 AOA 定位、TDOA 定位以及 TDOA/AOA 联合定位方法对辐射源的观测量均为非线性函数，因此线性卡尔曼滤波将不再适用，非线性滤波算法就变得尤为重要，本文主要针对EKF 算法和PF 算法进行理论分析。

粒子滤波

目前粒子滤波算法广泛应用于移动机器人、图像处理、目标定位、导航以及跟踪等领域，它是基于贝叶斯滤波框架下的滤波算法，其本质就是利用系统当前和过去的观测量来估计未知参数的当前值。相比于 EKF以及 UKF 算法，PF 算法不需要对非线性状态方程线性化，收敛较快且定位精度较高。

GAN 网络的训练过程主要是在平衡的基础上减少D 网络与G 网络的损失函数值的过程，这样才能满足纳什均衡。GAN 网络的损失函数如公式（14）所示：

由于，G 网络的优化目标为使G(z)与x分布相似，即让D(G(z))输出为1，因此其函数表达式如公式（15）所示；D 网络的优化目标为使D(x)输出为1，使D(G(z))输出为0，故D 网络的优化函数如公式（16）所示；整个GAN 网络的优化函数如公式（16）所示。

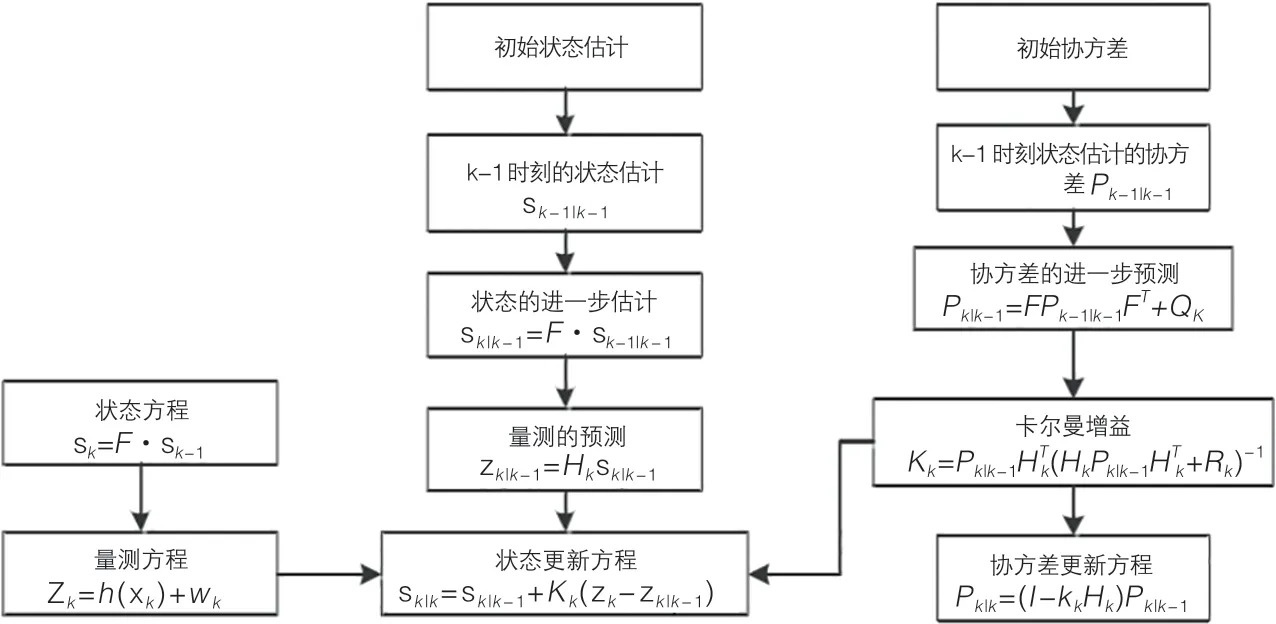
图6 扩展卡尔曼滤波流程图

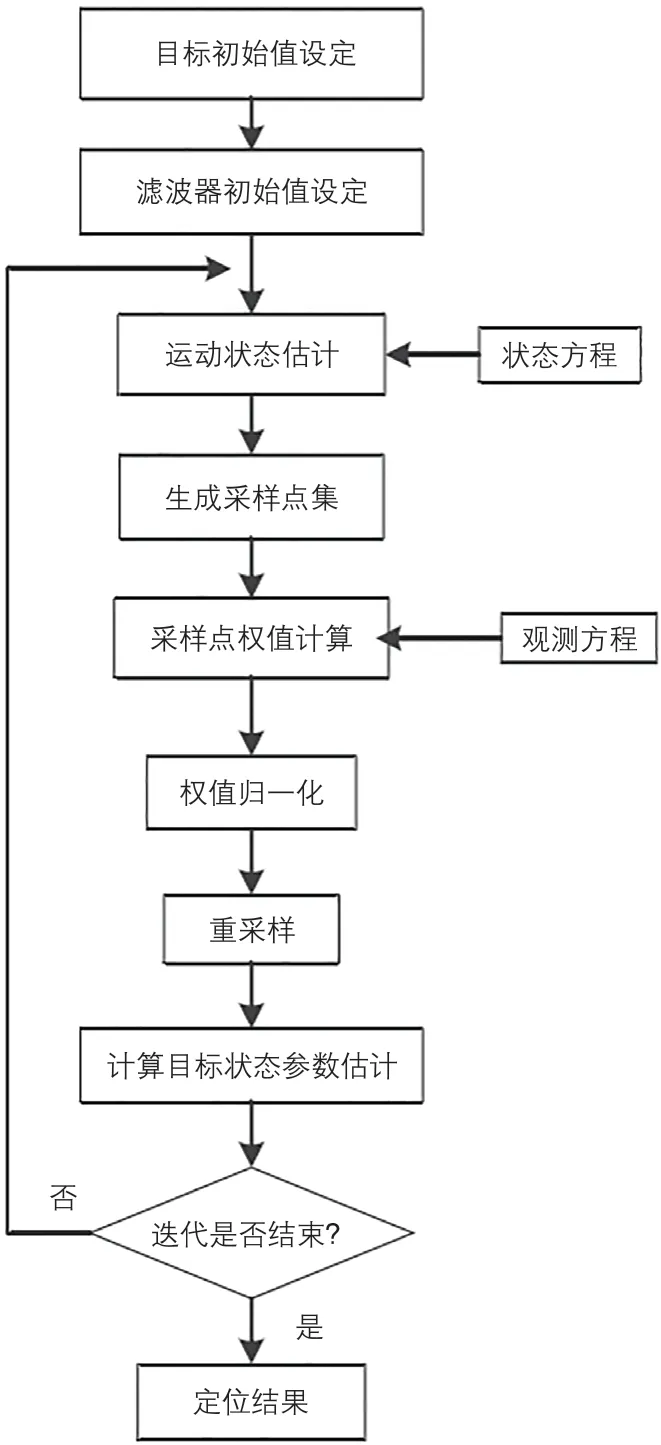
图7 粒子滤波流程图

无人机单步最优航迹规划算法

CRLB 和FIM 相互作用，因此可以通过FIM 获得CRLB。为了解决FIM 问题，我们需要知道发卡机制在哪里，但实际上这个值是未知的。我们将用发射机的实际位置替换滤波器的计算值，使其接近FIM。根据无人机运动模型以及约束条件，目标函数可以表示为

目标函数：

约束条件：

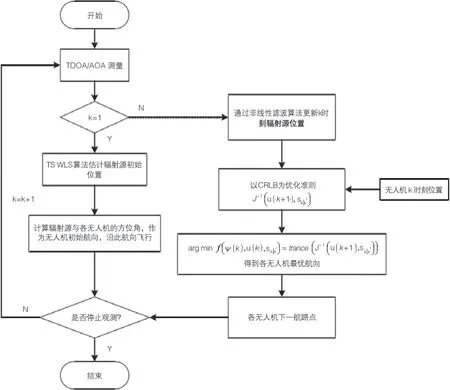
图8 多无人机基于 TDOA/AOA 定位方法的航迹规划流程图

调整结果

多无人机基于TDOA 定位与TDOA/AOA 联合定位性能比较：

3 结论

首先总结了几种简单被动定位方法的基本原理，包括AOA 定位、时差测定、FDOA 定位和RSSI 定位。从理论上推导并分析了这些方法的定位精度。但由于单点定位算法定位精度有限，需要结合这些定位算法，建立和分析无人机运动模型和辐射源状态，为多点跟踪的优化跟踪提供理论依据。

首先介绍了时空/ 频率定位联合算法模型，分析了用CWLS 算法确定移动辐射源位置和速度的方法，并从理论上推导出CRLB 联合定位系统。其次，通过仿真分析了无人机时差测量中随机误差、频差测量误差、位置和速度对定位精度的影响。最后，对用于多架无人机的来源进行了识别和跟踪研究。结合非线性滤波算法，建立了辐射源跟踪模型.通过最小化CRLB传感器的位置，优化多架无人机的轨迹。仿真表明，轨迹优化可以提高定位精度和稳定性。

本文研究了二维空间辐射源定位和跟踪的相关问题。但在实践中，无人机的飞行高度也会影响定位精度，因此需要考虑飞行高度。确定和跟踪被动空间无人飞行器的方法需要进一步发展。

在规划多架无人机的飞行轨迹时，只考虑每架无人机在某一时刻的最佳飞行控制矢量，以取代其位置。如果预先预测多级路径的优化，定位精度会提高，但计算会呈指数增长。然后我们可以研究多阶段简化计算和优化路径问题。

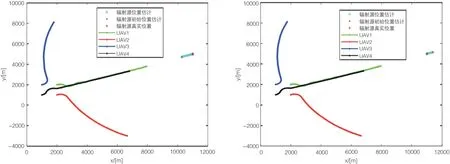
图9 TDOA/AOA 定位基于 EKF 航迹规划

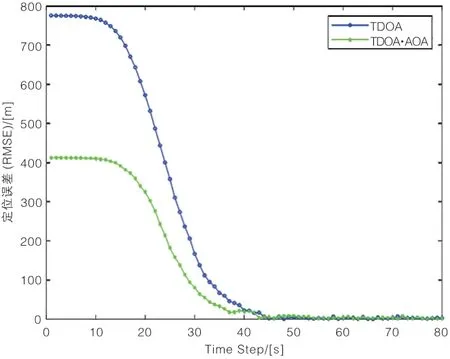
图10 辐射源位置估计的均方根误差比较图