基于IMO 与PCHD 模型的MMC- APF 控制策略研究
王玉娇,彭 程*,李 燕,张树红,于 雪,马 丽
(河北水利电力学院,河北 沧州)
引言
当前,针对MMC-APF 的研究与实际工程日益增多[1],相应的控制策略按照建立数学模型的坐标系的不同,可以分为两类。一类是通过对两相静止坐标系特征量研究采取的控制方法:文献[2]对运行中MMC的交流网侧电压与功率的关系进行分析,得出交流电压与系统功率之间的数学模型,提出了一种新的控制方法,但补偿效果不明显,另一类是在旋转坐标系中进行控制研究:文献[3]利用辅助式控制器进行控制,抑制了环流中的负序电流成分、交流电网侧产生有功功率的波动、无功功率的波动。该方法在内环控制过程中,会因为系统的电压变化、干扰等因素,降低最终的谐波补偿效果。
在基于PCHD 模型的PBC 控制基础之上[4],设计一整套基于IMO 和PCHD 模型的PBC 控制的系统,在稳态与电网电压跌落状态下分别进行PBC 控制、基于IMO 和PBC 的控制仿真,进一步降低了电网谐波含量、减少电网波动造成的谐波补偿精度的降低。
1 MMC-SAPF 的一般数学模型
图1 为MMC-SAPF 主电路结构。图中,usj(j=a,b, c)为三相交流电源电压;isj为三相交流电源电流;iLj为三相负荷电流;ifj为三相SAPF 补偿电流;负载由三相整流桥与阻抗RL、LL构成;负载所连线路阻抗为R1、L1;
由图1 可得MMC-SAPF 交流侧的数学模型分别为

图1 MMC-SAPF 主电路结构

2 基于IMO 与PCHD 模型的控制策略
2.1 控制策略


2.2 整体控制原理框图
如图2 所示,将提取出来的信号经过坐标变换,得到IMO 与PCHD 模型控制器的输入。将控制器得到的信号进行载波移相调制,实现对电流、电压的动态稳定控制。
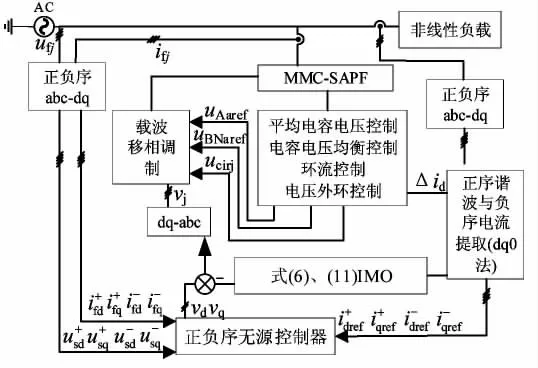
图2 基于IMO 与PCHD 模型的PBC 整体控制框图
2.3 仿真结果及分析
在Matlab/Simulink 中,搭建基于MMC-APF 的仿真系统,并在系统稳定状态、电压跌落状态下分别进行仿真对比验证。系统参数见表1。

表1 系统参数
2.3.1 稳定状态
仿真结果见图3,负载电流波形发生严重畸变,谐波补偿前三相THD%分别为26.77%、26.78%、26.77%。单独采用PBC 时,三相电流THD%分别为2.45%、2.45%、2.44%,满足电网对谐波的要求。采用PBC+IMO 时三相电流THD%分别为1.66%、1.66%、1.71%,相比单独采用PBC 谐波畸变率进一步降低,验证了本文所设计的基于IMO 与PCHD 模型的PBC 系统在谐波补偿控制中的优势。

图3 稳态下仿真波形
2.3.2 电压跌落状态
设置B 相电压跌落10%,电压仿真结果见图4。

图4 电压跌落时仿真波形
补偿前电压跌落导致负载电流三相不平衡且谐波含量大。单独采用PBC 控制时,三相电流THD%分别为2.51%、2.54%、2.51%,满足电网对谐波的要求。采用PBC+IMO 时三相电流THD%分别为1.68%、1.68%、1.77%,同样验证了本文设计的控制系统在谐波补偿控制中的优势。
3 结论
本文所研究的MMC-APF 在电网谐波治理方面具有重要的地位,基于MMC-APF 的控制系统是当今众多专家学者研究的热题。本文通过设计PBC+IMO 的控制系统并经过Matlab/Simulink 平台仿真,得出以下结论。
(1)PBC+IMO 控制系统,能够进一步的改善系统波动下的谐波补偿精度,从而进一步提高了电网电能质量。
(2)电网在运行过程中时刻处于动态的变化之中,这种动态变化除本文所涉及的电压跌落的情况之外,还包括电网负荷切换、电网参数发生变化等,本文设计的控制系统,同样适用于电网其他因素导致的参数波动的状态,对电网实际运行下的控制具有较广的借鉴意义。

