有机物热值的计算方法

张 玉，张林进，杨亮军

（1.江苏中圣园科技股份有限公司，江苏南京211102；2.陕西恒源投资集团电化有限公司，陕西榆林719300）

在化工、冶金、制药、石油、造纸、奶制品加工、食品罐装等多种工业生产过程中，会排放大量有机废气和有机废液[1]。在所有有机废气和有机废液的处理方法中，焚烧法具有技术成熟、占地面积小、处理速度快、污染物去除彻底、可回收能量等优点，现已成为包括发达国家在内应用最为广泛的一种处理技术[2-6]。

我国工业的快速发展使得有机废气和有机废液的生成量越来越大，因此关于焚烧法处理有机废气和有机废液的设计案例也越来越多。大量学者[7-12]在设计废气和废液焚烧装置时，都会不约而同地强调焚烧温度的重要性，并指出有机物的热物性参数是设计过程中不可或缺的部分。其中，燃料热值的高低是关乎到工艺路线、余热回收量、设备尺寸、投资成本的关键因素之一[13]。无论是有机废气还是有机废液，在从设备中排出时都会受到工艺的影响而变为成分复杂的混合物，包含多种可燃成分。对于有机废气而言，通常需要在设计手册或数据库中查询各个组分的热值，然后根据各组分的分压计算出混合废气的综合热值。对于有机废液而言，尽管有汪晓军[14]、别如山[15]、Michel[16]提出的热值计算方法，但目前工程上应用最为广泛的还是门捷列夫公式。

式中，C、H、O和S分别为燃料中碳、氢、氧、氮和硫的质量百分比。

燃烧过程就是将储存在化学键中的能量转变为热量[17]。对于种类繁多的有机物而言，即使分子式相同，燃烧产生的热量也会因键能的差异而有所区别。门捷列夫公式在计算燃料热值时，仅以分子式作为唯一判据，并未考虑化学键不同导致的热值变化。特别是部分气态燃料（例如乙炔），使用门捷列夫公式计算热值时极易出现误差偏大的问题，因此一些燃烧教材中会指出门捷列夫公式仅适用于液态燃料和固态燃料的热值计算。

然而经调研却发现，在焚烧法的工艺设计过程中，由于废气和废液的有机物成分较多，工程技术人员通常会直接使用门捷列夫公式一并计算热值，导致经常出现设计结果偏差较大的问题。针对目前焚烧法工艺设计过程中，有机废气和有机废液的热值采用查表计算繁琐、采用门捷列夫公式计算误差较大等问题，本文提出了一种新的有机物燃烧热值计算方法。

1 有机物燃烧热值计算

通过燃烧前后的焓值变化计算燃烧反应放热量是一种常用的热值计算方法[18]。对于仅含C、H、O三种元素的有机物燃烧化学反应式和燃烧反应热计算公式如下：

式中：ΔrHΘ为燃烧反应热，kJ/mol；a、b、c分别为化学反应系数；为CO2标准生成焓，-393.51 kJ/为H2O 标准生成焓，-241.81 kJ/mol；为有机物M标准反应焓，可查表获得；为O2标准反应焓，0 kJ/mol。

只需要从设计手册或数据库中查出有机物M的标准反应焓（如果为气态有机物，标准反应焓为如果为液态有机物，标准反应焓为便可计算得出燃烧反应热，即燃料低位热值。

1.1 气态有机物

本文在整理常见有机物燃烧热值时发现，对于同一类型的有机物（例如甲烷、乙烷、丙烷和丁烷）而言，热值与其C原子数基本呈线性关系，即分子式每增加CH2，热值都会提升近似相等的数值。这是因为每增加一个C原子意味着将增加一个C-C键和两个C-H键，尽管在不同结构条件下，不同位置处C-C键和C-H键的键能有所区别，但整体而言偏差不大（例如在丙烷中，外侧C-H键的键能为（422.5±2.1）kJ/mol，而中心C-H键的键能为（410.7±2.9）kJ/mol[19]）。于是，根据上述规律可以写出有机物燃烧低位热值与C原子数量的近似关系式，该公式对于其相同种类的同分异构体也适用，表达式如下：

式中：QL为有机物低位热值，kJ/mol；A和B1为有机物低位热值的计算参数，由有机物种类决定，可根据现有设计手册或数据库中各种有机物热值拟合得到；xC为有机物分子式中的C原子数量。

大学生往往喜欢与志同道合，有相同兴趣爱好的人处事，这也有利于他未来的职业发展，他们正需要一个专业的平台来结交益友。

同时，对门捷列夫公式（1）稍加处理后可得到有机物低位热值与有机物分子式中各原子数量的关系：

式中：QL为有机物低位热值，kJ/mol；xC、xH、xO、xS分别表示燃料分子式中的C、H、O、S原子数量。

在式（4）中，当xO和xS为定值时，随着分子式每增加CH2，有机物低位热值的变化量ΔQ=612.8 kJ/mol ，于是门捷列夫公式（1）也可以写成如下形式，其中B2的数值由有机物分子式决定。

对比本文所提出的公式（3）和门捷列夫公式变换后的公式（5），可以发现两者形式几乎相同。区别在于公式（5）中的系数为定值，且B2仅根据分子式确定，忽略了不同种类有机物中特殊官能团键能带来的差异；而公式（3）中有A和B1两个参数，其数值均由有机物种类决定。

例如，对于醛类和酮类而言，其分子式均为CxH2（x+1）O，当采用公式（5）计算时，两者低位热值均为QL=612.8xC-174.40 ，而采用公式（3）计算时，两者低位热值则分别为QL=610.88xC-98.41 和QL=613.09xC-149.02 ，存在一定差异。

图1分别给出了文献中所记载的醛类与酮类有机物低位热值以及公式（3）和公式（5）计算得到的低位热值，从中可以看出，随着C原子数的增加，两种物质热值的变化趋势近似为一条直线，这与两个公式给出的数学形式一致。尽管醛类和酮类有机物的分子式完全相同，但实际热值却存在一定的差异，因此公式（5）无法同时较为贴近地拟合两种有机物热值。而公式（3）中的参数A和B1是由有机物种类所决定，即醛类和酮类所对应的A和B1值并不相同，所以可以分别得到两根与实际数据更为贴近的直线。

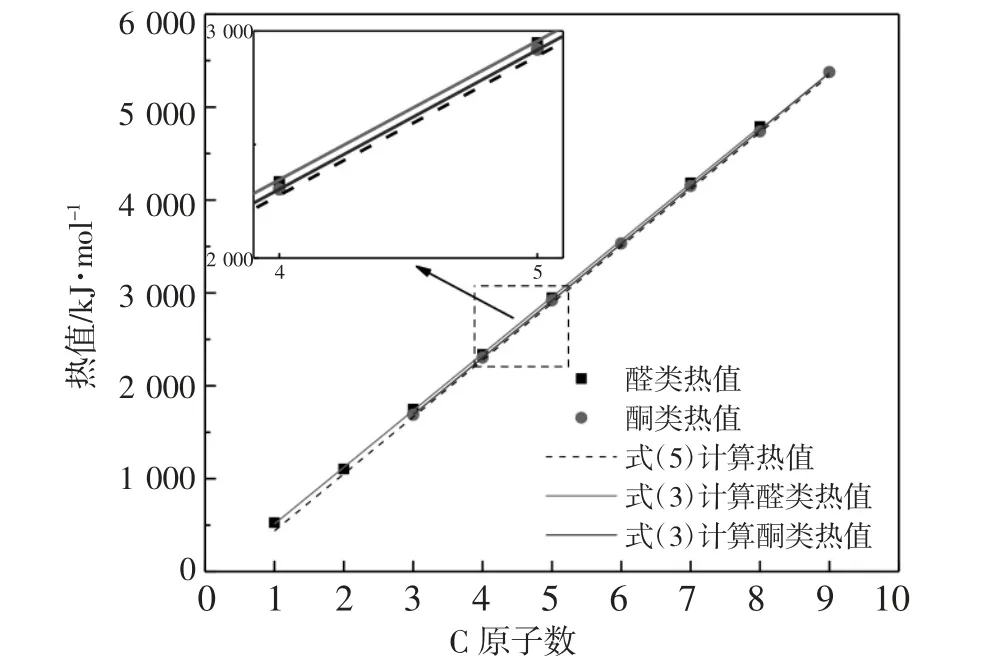
图1 酮类与醛类低位热值对比图

图2 酮类与醛类低位热值计算误差图

表1给出了公式（3）中不同类型有机物低位热值计算时A和B1的具体数值。图3和图4分别是根据公式（3）和公式（4）得出的气态有机物低位热值计算误差，有机物的基准热值数据来源于化工物性数据手册和网络数据库[20-21]。从这两幅图中可以明显看出，公式（3）的计算结果误差普遍在3%以下；而公式（4）得出的结果中，误差普遍较高，甚至还有两个超过16%。不过随C原子数量的增加，即有机物相对分子质量的增加，无论是公式（3）还是公式（4）的计算误差都开始逐渐减小。上述现象表明，利用公式（4）计算有机物热值是有限制条件的，并非所有情况均适用，特别是对于部分相对分子质量较小的有机物，极易出现计算结果误差偏大的问题。归根结底还是因为公式（4）未考虑官能团的影响。但本文所提出的公式（3）在计算有机物热值时，根据有机物类型所选取的双参数已经将官能团的影响考虑在内，所以计算误差随相对分子质量的变化波动较小。公式（3）计算的结果精度完全可应用于工程项目设计中。

表1 常见不同类型气态有机物低位热值计算参数

图3 气态有机物公式（3）热值计算误差图

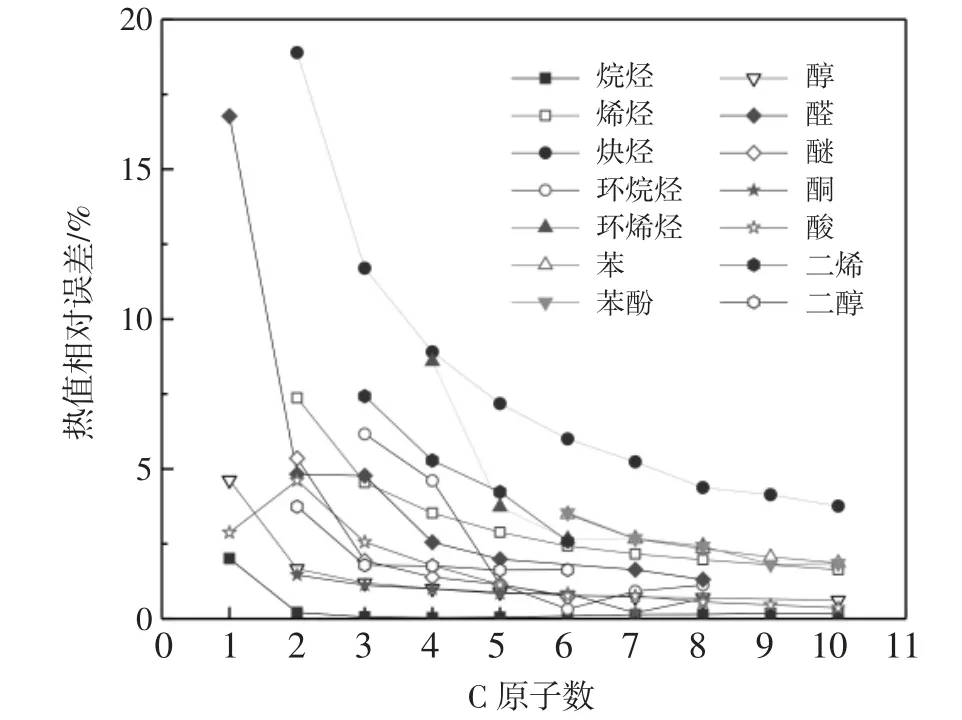
图4 气态有机物公式（4）热值计算误差图

1.2 液态有机物

对于液态有机物而言，必须先在炉膛内吸收热量蒸发成气态后才能与氧气发生剧烈氧化还原反应，释放热量。因此同种有机物在液态和气态下燃烧释放的热量差异仅取决于其由液态等温蒸发成气态时所吸收的热量，于是可根据下式计算得到低位热值的变化量：

尽管有机物标准气化热相较于燃烧生成热而言较小，但仍然会对计算误差造成不可忽略的影响，所以必须对表1中的参数进行修正。表2给出了公式（3）中液态有机物低位热值的修正后计算参数。

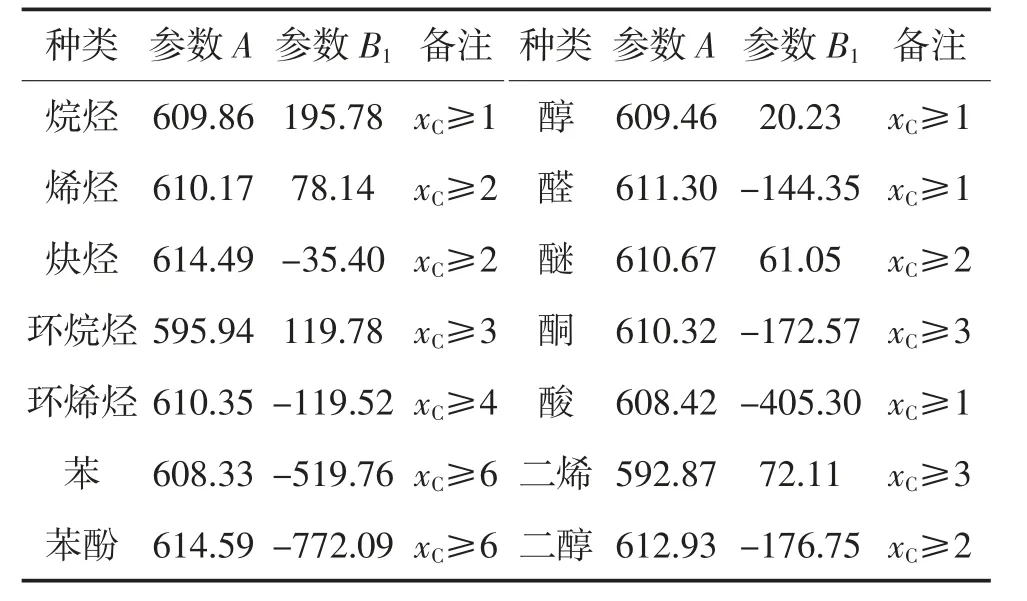
表2 常见不同类型液态有机物低位热值计算参数

图5和图6是公式（3）和公式（4）得出的液态有机物热值计算误差，对比图3和图4可以发现，两个公式计算液态有机物低位热值时的精度从整体上看比气态有机物更高。但公式（4）中的酸类有机物热值却存在极大的误差。当C的数量为1时，酸类有机物对应的物质为甲酸，甲酸虽然在常温下为液态，但其相对分子质量相较于其他液态有机物而言较小，且羧基所含键能占总键能的比例较大，导致出现高达25.58%的计算误差。若将图6中甲酸和乙酸的数据除去后，再使用公式（4）计算，此时得到的液态有机物低位热值误差便均低于8%，计算精度大幅度提升。上述问题表明，并非所有常温下的液态有机物热值均可以使用门捷列夫公式计算，燃烧教材中所指出的液态燃料和固态燃料的使用限制条件，其真正含义应是：门捷列夫公式在计算相对分子质量较大的燃料热值时有着较高的精度。而大部分液态燃料和固态燃料恰好满足这一特性。所以在使用门捷列夫公式计算燃料热值时，相对分子质量也是需要被考虑在内的因素之一。不过，对于本文所提出的公式（3）而言，参数A和B1也考虑了有机物所处状态的影响，因此依旧能保持较高的计算精度，有机物的状态和相对分子质量不会再次对热值产生显著的影响。

图5 液态有机物公式（3）热值计算误差图

图6 液态有机物公式（4）热值计算误差图

2 有机物热值的简化计算

虽然公式（3）的计算精度较高，但对于每一种有机物而言，都需要确定两个参数，这无疑增加了计算的复杂性。对此，本文将通过降低一定的计算精度来对公式（3）简化，将气态有机物（表1）与液态有机物（表2）中的计算参数A进行平均取值，简化后的表达式为：

式中：QL为有机物低位热值，kJ/mol；B3为热值的计算参数，由有机物种类和状态所决定。

简化后的公式仅需要一个单独的参数B3即可计算得到有机物低位热值，B3的数值通过表3得到。尽管简化后的单参数公式计算精度会有所下降，但最大误差依旧低于3.5%，如图7和图8所示，完全符合工程计算的精度要求。

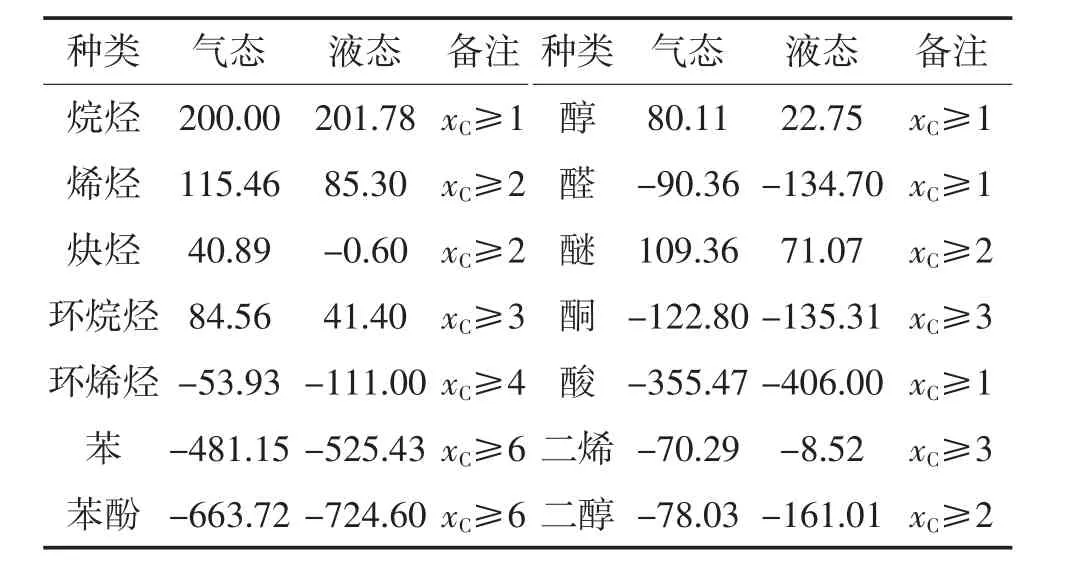
表3 常见不同类型气态、液态有机物低位热值计算参数B3取值

图7 气态有机物简化公式热值计算误差图

图8 液态有机物简化公式热值计算误差图

3 总结

针对目前焚烧法工艺设计过程中，有机废气和废液的热值采用查表计算繁琐、采用门捷列夫公式计算误差较大等问题，本文提出了一种新的热值计算方法。将该计算方法与门捷列夫公式的计算结果进行对比，结果表明：门捷列夫公式未考虑官能团的影响，所以在计算分子量较小的部分有机物热值时容易产生较大误差；而本文提出的计算方法中，两个参数均由有机物种类和所处状态决定，已经考虑过官能团的影响，因此既可以较为准确的计算分子量较小的有机物热值，也可以更为精准地得到分子量较大的有机物热值，整体计算误差不超过3%。此外，考虑到双参数计算公式的不便，提出了降低部分精度的单参数简化热值计算公式，该简化公式依旧能保证常见类型有机物的低位热值计算误差不超过3.5%。