基于改进的SSA 优化BP 神经网络的导水断裂带高度预测
王耀国,李勇永,郭 涛
(1.洛阳市规划建筑设计研究院有限公司,河南 洛阳 471000;2.洛阳职业技术学院,河南 洛阳 471000;3.洛阳理工学院 土木工程学院,河南 洛阳 471000;4.洛阳师范学院 国土与旅游学院,河南 洛阳 471000;5.四川省农业科学院 遥感与数字农业研究所,四川 成都 610066)
导水断裂带不仅是井下突水事故和高位孔预抽煤层瓦斯事故的主要通道,其高度也是建立采煤沉陷灾变预警模型的关键参数,对煤矿井下安全开采具有重要意义[1]。目前,探测导水断裂带高度的主流方法为现场实测法[2],由于煤矿构造格局、开采方式存在较大差异性,导致导水断裂带高度形成具有复杂性和多因素影响的特点。然而,传统导水断裂带高度计算的经验公式中参与计算的变量较少,计算结果波动较大,精度难以保证[3]。
近年来,许多学者提出通过机器学习算法内在逻辑代替人为考量非线性关系,提高导水断裂带高度预测准确度。李振华等[4]提出构建BP 神经网络模型对导水断裂带高度进行预测,预测结果准确度优于公式计算方法,但BP 神经网络收敛速度慢,易陷入局部极值等缺点较为突出;谢晓峰等[5]通过对样本数据进行主成分提取建立PCA-BP 预测模型,以提高收敛速度和预测精度;施龙青等[2]建立基于PCA-GA-Elman 的导水断裂带发育高度预测模型,采用遗传算法(GA)优化Elman 神经网络,预测准确率较高,但因GA 的操作复杂从而导致寻优速度较慢;娄高中等[6]利用粒子群算法(PSO)优化BP 神经网络,预测结果准确性较高,且收敛速度快,却易陷入局部最优解。为弥补上述研究成果的不足,进一步提升模型实用性,采用最新提出的麻雀搜索算法(SSA)对BP 神经网络进行优化,并引入Tent 混沌映射、高斯变异、高斯扰动和动态步长因子对标准SSA 进行改进,提高BP 算法的全局搜索和跳出局部最优的能力,增强其优化性能,为导水断裂带高度预测探索1 种新的优化策略和模型。
1 麻雀搜索算法改进原理及模型优化
1.1 麻雀搜索算法原理
麻雀搜索算法(SSA)是2020 年首次提出的一种基于麻雀群体行为的智能优化算法,通过对麻雀群体寻找食物和逃避被捕猎的行为进行深入研究,将不同的麻雀个体进行分类,以麻雀个体位置的不断更新实现智能优化的目的[7]。在麻雀种群中寻找食物能力较强的个体称为发现者,其持续搜索食物,确定整个麻雀种群寻找食物的范围和路径;除发现者之外,其它的个体追随发现者觅食,称其为跟随者,二者角色在一定条件下可以互换;从麻雀种群中抽取一定比例的个体承担种群的侦查警戒任务,称其为预警者,当种群出现危险时,其发出警告并放弃食物[8]。采用将尽20 个包含单峰、多峰以及固定维度的标准测试函数对SSA 算法的性能进行验证,结果表明:SSA 算法在搜索精度、收敛速度、稳定性和避免局部最优值方面比现有常见优化算法具有明显的优势,为解决复杂的全局优化问题提供了一种全新的方法[9]。
将麻雀种群用一个n×d 维矩阵X 表示,d 为待优化变量的维数,n 为麻雀的数量,那么麻雀的初始位置如式(1):
麻雀种群的适应度值F 表示如式(2):
式中:F(X)为适应度函数;Xi为第i 只麻雀的位置;f(Xi)为麻雀个体的适应度值。
发现者的位置更新如式(3):
式中:k、Tmax分别为当前迭代次数和设定迭代次数;α 为1 个随机数,α∈(0,1];Q 为1 个服从正态分布的随机数;R2为预警值,取值[0,1];ST 为安全值,取值[0.5,1];L 为1×d 的矩阵;
当R2≥ST 时,发现者带领所有麻雀立即飞离存在危险的区域。
为抢夺发现者的食物,跟随者的位置随时可以做出调整,跟随者的位置更新如式(4):
式中:Xp为当前麻雀觅食的最佳位置;Xw为当前麻雀觅食的最差位置;A 为元素,是1 或-1 的1×d 的矩阵,且满足A+=AT(AAT)-1。
选取每代产生的新种群的10%~20%个体作为预警者负责警戒,麻雀种群觅食过程中,如有天敌靠近时,预警信号将使整个种群放弃食物而转移到安全位置,预警者的位置更新如式(5):
式中:Xb为多次迭代后全局最优位置;β 为步长控制参数;K 为麻雀个体飞行方向的步长调整系数,其为取值[-1,1]的随机数;fi为当前第i 只麻雀的适应度值;fg、fw为当前迭代次数下整个种群的全局最优和最差适应度值;ε 为最小常数,避免分母为0。
当fi>fg时,表示当前第i 只麻雀位于种群的边缘,极易遇到危险;当fi=fg时,表示位于种群中间的麻雀也察觉到了危险,需要向其他麻雀靠拢,以降低被捕食的概几率[10]。
1.2 Tent 混沌映射算法
Tent 混沌映射是一种分段的线性二维混沌映射,其具有均匀的分布函数和良好的相关性,在其参数的取值范围内,该非线性系统处于混沌状态,呈现出不确定性、唯一性和不可预测的特点,能够在一定范围内对麻雀种群的状态进行不重复遍历。Tent 映射表达式如式(6):
式中:Hi为在i 时刻的混沌映射数值;α 为混沌系数。
在传统SSA 中,采用随机数对种群初始化,混沌映射模型与随机数种群初始化对比如图1。
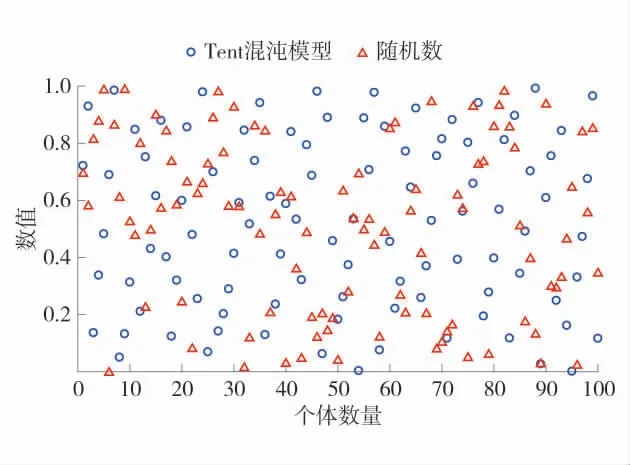
图1 混沌映射模型与随机数种群初始化对比Fig.1 Comparison between chaotic mapping model and random number population initialization
图1 中三角形和圆形分别表示随机数和混沌模型初始化值。图1 直观显示三角形在一些区域分布集中,导致在某些区域取值出现空白,而圆形则分布均匀,因此Tent 混沌映射模型对种群进行初始化,能够增强种群的多样性和分布均匀性。通过Tent 混沌映射模型对发现者、追随者和预警者位置进行更新,使其具有更强的全局寻优能力[11]。
1.3 高斯变异和高斯扰动算法
1)高斯变异。是指从均值为μ、方差为σ2的正态分布中抽取1 个随机数,置换SSA 算法中的参数变量[12],达到优化算法的目的。根据正态分布曲线的分布特点,高斯变异的主要搜索范围为原个体附近的某个区域。因此,高斯变异的特性决定其具有较强的局部搜索能力,对涉及多峰函数的优化问题,有利于算法高效、准确地找到全局极值点。为此,结合Tent 混沌映射和高斯变异,统筹全局搜索和局部探索能力,旨在提高SSA 的收敛速度和进化性能[13]。高斯变异公式如式(7):
式中:Tg为原参数高斯变异后的数值;T 为原来的参数变量;N(0,1)为期望值为0,标准差为1 的正态分布随机数。
2)高斯扰动。为提升SSA 跳出局部最优解的能力,对每一次迭代后的麻雀个体最优位置进行高斯微小扰动,帮助其更好地逃离局部最优区域[13],高斯扰动表达式如式(8)和式(9):
式中:Gb为每次迭代麻雀的最优位置;G 为高斯扰动前麻雀的适应度,Gaussian(μ,σ2)为均值为μ、方差为σ2的高斯函数;NGtb为扰动后麻雀个体的最优适应度;Gt为第t 次迭代麻雀个体最优适应度。
1.4 动态调整步长因子
在麻雀种群中负责警戒的预警者通过式(5)更新位置,其中的步长参数β 和K 用来调节全局搜索能力和局部开发能力,其取值为限定范围内的随机数,很难有目的和规律的探索最优解空间,存在一定的盲目性,容易使SSA 陷入局部最优解。在SSA迭代初期,麻雀种群多样性较高,算法具有较强的全局搜索能力,需通过设置较小的步长加强局部搜索能力。当麻雀个体全部朝向全局最优移动时,探索空间将大大减小,可能会造成收敛过早,此时设置较大的参数值能使麻雀避免局部最优。因此步长参数需具有在迭代过程中先递增后递减的动态特征,在初期利用较小步长充分对搜索空间进行探索,后期利用较大步长提高收敛速度,提高SSA 的寻优精度[14]。改进动态步长参数如式(10)和式(11):
式中:t 为当前迭代次数;ts为设定迭代次数;rand 为随机数。
1.5 改进的SSA-BP 模型
采用BP 神经网络预测导水断裂带高度时,训练集数量保持不变的情况下,影响预测精度的主要因素为BP 神经网络初始化权值和阈值2 项参数。该参数的取值通常由BP 算法随机生成或者通过操作者手动进行调试,从而导致构建的BP 神经网络模型预测精度低、收敛速度慢,甚至出现“过拟合”[15]。鉴于此,利用改进的SSA 对BP 神经网络的权值和阈值进行优化,构建改进的SSA-BP 优化模型。改进的SSA-BP 模型预测流程如图2。
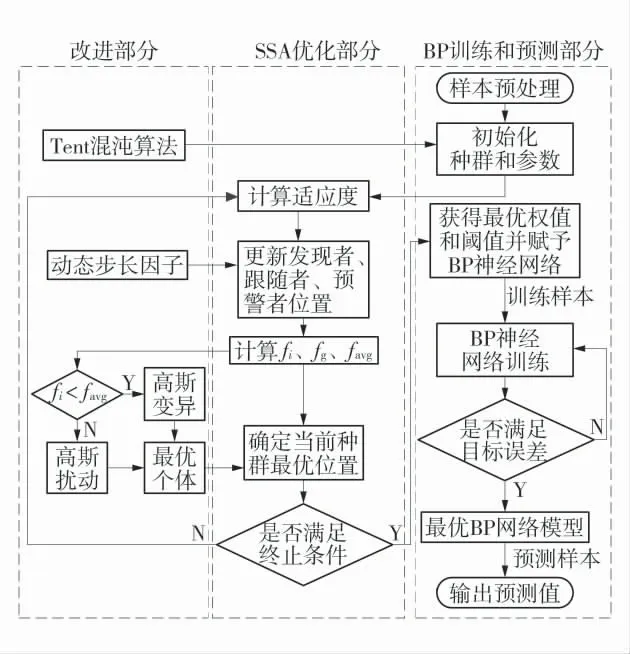
图2 改进的SSA-BP 模型预测流程Fig.2 Improved SSA-BP model prediction process
在改进模型中用种群内每个麻雀个体反映BP神经网络的权值和阈值,引入Tent 混沌映射算法,增加麻雀种群遍历性。在麻雀个体位置更新中,favg为种群平均适应度,当fi<favg时,麻雀群体出现集聚现象,采用式(7)实施高斯变异,通过对比确定最优个体;当fi≥favg时,麻雀种群开始表现出发散状态,按式(8)和式(9)进行高斯扰动,对比确定最优个体[13]。在预警者位置更新中采用动态步长因子,增强算法搜索能力。
2 导水断裂带高度影响因素及样本数据
2.1 导水断裂带发育高度主要影响因素
在地下煤层采动影响下,顶板导水断裂带的形成受到众多因素影响,根据《煤矿防治水细则》[16]及前人研究成果,将导水断裂带发育高度影响因素分为3 大类,分别为地质构造、岩石特性和开采活动[17]。
1)地质构造相关的因素有煤层的埋深、地下煤层的倾斜角度、煤层硬度等。
2)岩石特性相关的因素包含顶板覆岩结构、强度、破碎程度等。引入硬岩岩性比例系数,用来反映岩层单轴抗压强度与顶板结构综合影响,通过导水断裂带高度范围内硬岩岩层的累计厚度与预估导水断裂带高度的比值对综合影响进行量化[18]。
3)开采活动相关因素有开采厚度、工作面倾斜长度、开采进度等。一般情况下,采厚与导水断裂带高度之间呈近似分式函数关系[19]。随着开采工作面倾斜长度增加,导水断裂带高度呈台阶状或分式函数增长[20]。
2.2 样本数据选取
根据前人对导水断裂带高度影响因素的研究,选择采深、采厚、工作面斜长、硬岩岩性比例系数4个影响因子和实测导水断裂带发育高度组成5 维样本数据,作为输入模型的数据。依据选择的导水断裂带高度主要影响因素,收集到国内部分矿区导水断裂带高度实测样本数据[21],导水断裂带高度的部分样本数据见表1。

表1 导水断裂带高度的部分样本数据Table 1 Part of the sample data for the height of water flowing fractured zone
采厚取值1.7~9 m,岩性比例系数取值0.06~1,工作面斜长分布在55~222 m 区间,采深分布在49~679 m 区间,导水断裂带高度取值20~86.8 m。各个属性数据的梯度分布广泛,每个样本各具代表性,有效降低样本数据分布的集中化程度,训练的模型预测适用性更强。选取1#~42#例作为训练样本,43#~48#作为检验样本。
3 模型应用与精度评价
3.1 模型参数设置
为验证改进SSA-BP 预测模型的有效性和准确性,借助MATLAB R2016b 计算平台,将1#~42#例5维样本数据输入模型并按照图1 流程进行训练,利用改进的SSA-BP 模型与SSA-BP、PSO-BP 以及BP神经网络模型的预测结果和性能评价指标进行对比。经过多次反复计算,得出当隐含层个数为9 时,BP 神经网络训练误差最小,因此,将构建4-9-1 结构的BP 神经网络,训练次数设置为5 000,学习率为0.1,目标误差为0.000 01。初始种群规模为20,最大迭代次数设为50 次;种群中预警者个数取种群数目的20%,预警值0.8。
3.2 模型训练
多次迭代后每代最优适应度变化曲线如图3,训练样本预测值与实测值对比如图4。
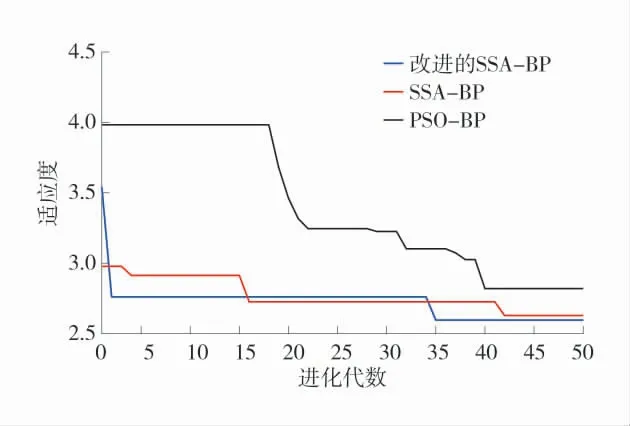
图3 适应度变化曲线Fig.3 The curves of fitness
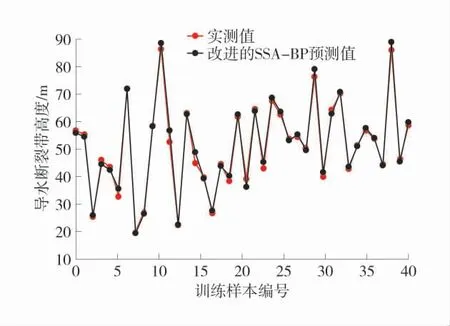
图4 训练样本预测值与实测值对比Fig.4 Comparison between predicted and measured values of training samples
由图3 可以看出:改进的SSA-BP 模型在迭代35 次后获得全局最优解,SSA-BP 和PSO-BP 模型在迭代42 次左右才趋于平稳,而文献[21]中GASVR 模型迭代45 次达到最优。表明改进的SSA-BP模型具有更快的收敛速度,全局搜索能力更强。
由图4 可以看出:采用训练好的模型对42 组训练样本进行预测,训练集的平均绝对误差(MAE)为1.27 m,平均绝对百分比误差(MAPE)为2.73%,优于其它模型,相比SSA-BP 模型,MAE 和MAPE 分别提升0.13 m 和0.18%,相比前人研究的GA-SVR模型,MAE 和MAPE 分别提升0.14 m 和0.36%。因此,采用一系列优化算法对SSA 进行改进,使得模型输出更加稳定,为解决导水断裂带发育高度预测问题提供了一种新方法。
3.3 模型预测结果
取43#~48#例导水断裂带样本数据作为检测样本,利用改进的SSA-BP 模型进行预测,为检验该模型在导水断裂带高度预测方面的有效性和优越性,采用同样的初始化参数,构建基于SSA-BP、PSOBP、BP 的预测模型。4 种模型预测值与实测值对比如图5。4 种模型预测结果绝对误差对比如图6。
由图5 可以看出:改进的SSA-BP 模型预测结果与实测值的整体接近程度最高,其次是SSA-BP模型,PSO-BP 模型和BP 模型预测值在43、44 以及48 例样本的偏离幅度较大,预测准确率较低。
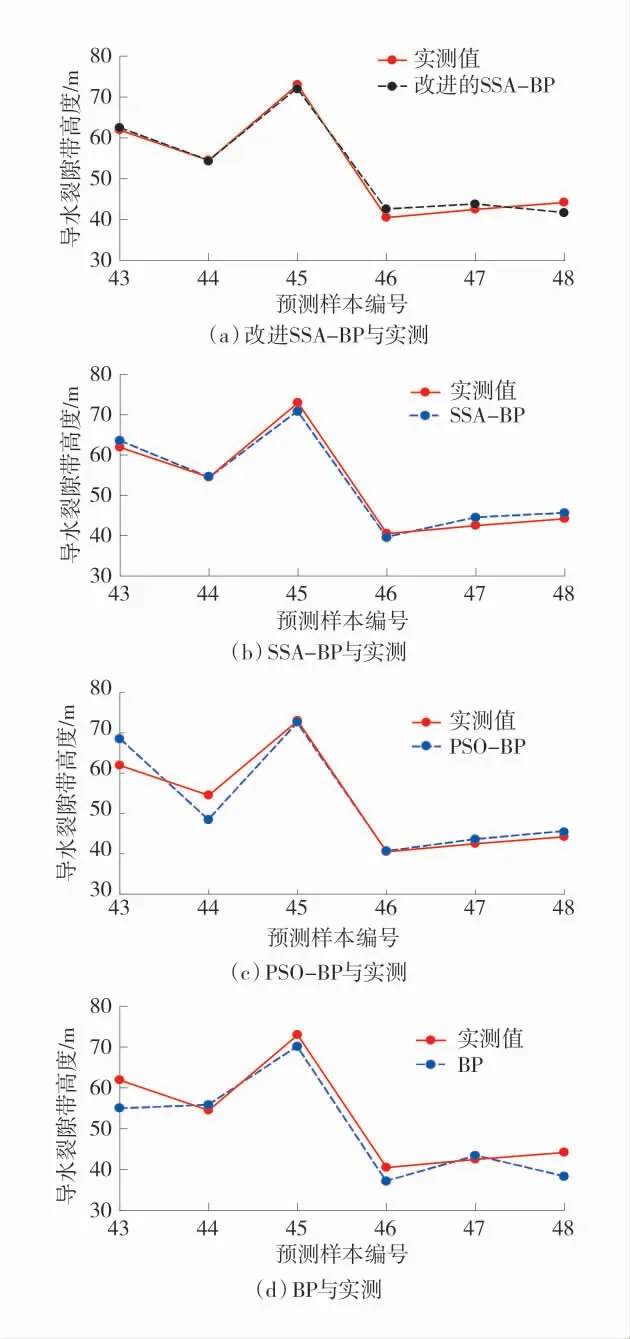
图5 模型预测值与实测值对比Fig.5 Comparison between the predicted values of the model and the measured values
由图6 可以看出:改进的SSA-BP 模型较其他模型绝对误差曲线最为平缓,平均绝对误差为1.23 m,优于SSA-BP 模型的1.37 m;PSO-BP 模型仅在在42 例和43 例样本的绝对误差较大,最大为6.53 m;而单一BP 模型的平均绝对误差为3.53 m,最大绝对误差高达6.87 m。同时,改进的SSA-BP 模型的平均绝对误差优于文献[21]中GA-SVR 模型的1.54 m。由此表明改进的SSA-BP 模型预测结果整体稳定性较好、准确度更高。
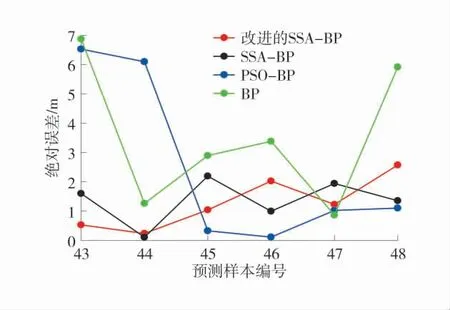
图6 预测结果绝对误差对比Fig.6 Comparison of absolute error of prediction results
3.4 模型预测精度
为了能够有效反映模型预测能力和预测结果的准确性,选择均方误差(RMSE)、平均绝对百分比误差(MAPE)和决定系数([R2])作为模型输出的评价指标,通过量化的数值对4 个模型预测的准确性和稳定性进行评价[22]。模型精度指标如表2。

表2 模型精度指标Table 2 Model accuracy index
由表2 可以看出:相较于SSA-BP、PSO-BP 和BP 模型,改进的SSA-BP 模型的RMSE 和MAPE 最优,较SSA-BP 模型分别提升0.09 m 和0.01%,显示出改进的SSA-BP 模型对导水断裂带高度预测方面具有一定优势。BP 模型的RMSE 和MAPE 最大,这是由于单一BP 模型在搜索过程中易陷入局部极值,且训练过程效率较低,甚至出现“过拟合”现象。对比4 个模型,改进的SSA-BP 模型的R2更接近于1,且比最差的BP 模型优化0.112,表明改进的SSA-BP 模型预测结果拟合程度高,预测结果更准确[23]。
因此,通过对比4 个预测模型的性能指标,提出的改进的SSA-BP 模型各项指标均为最优,可满足在导水断裂带高度准确预测的需要。
4 结 语
1)通过Tent 混沌、高斯变异、高斯扰动和动态步长因子等算法对SSA 进行优化改进,建立基于改进的SSA-BP 的导水断裂带高度预测模型,对比改进的SSA-BP、SSA-BP、PSO-BP 和BP 模型预测结果,改进的SSA-BP 模型在导水断裂带高度预测中准确率最高,达到97.36%。同时,预测结果较前人研究的GA-SVR 模型预测结果平均绝对误差提高0.31 m,平均绝对百分比误差提高0.40%,由此表明,基于改进的SSA-BP 的导水断裂带高度预测模型在预测准确度方面具有明显优势,可为煤矿安全生产提供可靠的分析和决策依据。
2)将改进的SSA-BP 模型用于导水断裂带高度预测研究中,样本数据只选择了几个有代表性且易于量化表达的影响因素,并且样本数量有限,在今后的研究中,进一步丰富样本数据影响因子类型和数量预测效果会更佳。另外,当训练样本数目较多时,研究的改进的SSA-BP 模型存在训练效率低、耗时长的缺陷,未来在提高算法计算效率方面需进一步优化提升,以提高模型在导水断裂带高度预测方面的实用性。

