单轴压缩下岩石全应力应变过程中能量演化特征
李东文,赵光明,刘之喜,孟祥瑞
(1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001;2.安徽理工大学 矿业工程学院,安徽 淮南 232001)
在采矿工程、地下工程等领域,工程设计通常以岩石的强度准则作为判断岩石稳定性的依据[1],但岩石是典型的非均匀非连续介质,其变形破坏力学响应与其内部的节理、裂隙等密切相关。而且利用岩石的应力-应变很难分析其动力破坏的机制,仅依靠岩石的应力-应变曲线进行工程设计,制约着工程设计精确度[2]。而在热力学领域内普遍认为物质物理变化的本质是能量转化,材料破坏的实质是能量驱动下的1 种失稳现象[3-7]。若能详细分析岩石全应力-应变曲线下的能量演化规律,建立利用能量变化判断岩石破坏的准则,有望更好地为工程实践服务。因此从能量角度来研究岩石变形破坏力学响应受到了学术界的广泛关注并取得了丰硕成果[8-13]。谢和平等[14]从能量的角度出发,利用能量的突然释放来描述岩石的失稳破坏;张志镇等[15]进行了红砂岩的单轴压缩试验,得到了试件吸收总能量、积聚弹性能、耗散能及弹性能占比与轴向应力的关系;宫凤强等[16]对多种不同岩石进行了单轴一次加卸载试验,发现了线性储能规律,提出了1 种分析岩爆倾向的新方法;刘之喜等[17]研究了红砂岩在单轴循环加卸载、单轴分级蠕变及蠕变后的单轴循环加卸载条件下的力学响应,得到了长期荷载对红砂岩的弹性能密度基本无影响。以往的研究多集中在单轴、三轴循环加卸载或分级加卸载过程中的能量演化规律,单轴压缩条件下岩石变形破坏全过程的能量演化规律研究较少,而后者是建立以能量变化判断岩石破坏准则的基础。因此,基于刘之喜等[18]提出的单轴分级加卸载各卸载点的弹性能是单轴压缩试验对应点的弹性能观点,选取花岗岩、砂岩和煤3 种代表性岩石进行单轴压缩和单轴分级加卸载试验,对比分析不同岩石峰前峰后能量演化规律。
1 试验概况
试验采用的试件有煤、砂岩和花岗岩。按照国际岩石试验标准试件的要求将煤、砂岩和花岗岩加工成高100、直径50 mm 的圆柱体。将每个圆柱体的端部用砂纸和磨片机研磨,使其两端的平行度小于0.05 mm,侧表面的平行度小于0.02 mm。
试验分为2 项内容:①煤、砂岩和花岗岩试件的单轴压缩试验;②煤、砂岩、花岗岩3 种试件的单轴分级加卸载试验。这2 种试验采用的都是RMT-150B 岩石力学测试系统。
砂岩和花岗岩单轴压缩试验的加载速率为0.5 kN/s,煤单轴压缩试验的加载速率为0.1 kN/s。根据3 种岩石试样单轴压缩强度来确定分级加卸载的试验方法,煤单轴分级加卸载试验的加卸载速率为0.1 kN/s,分级加载下限为0,上限分别为2.5、5.0、7.5、9.0 kN、…、直至试件破坏;砂岩试件单轴分级加卸载试验的加卸载速率为0.5 kN/s,分级加载下限为0,上限分别为10、20、30、40 kN、…、直至试件破坏;花岗岩试件单轴分级加卸载试验的加卸载速率为0.5 kN/s,分级加载下限为0,上限分别为60、80、100、120 kN、…、直至试件破坏。具体加载路径如图1。

图1 加载路径示意图Fig.1 Load path diagrams
2 试验结果
2.1 单轴分级加卸载试验结果
煤、砂岩和花岗岩的单轴分级加卸载应力-应变曲线如图2。
由图2 可知:当加载至卸载点卸载时,卸载曲线并不沿着原加载曲线下降,而是在加载曲线的下方。加卸载曲线并不重合,表明岩样吸收的总能量密度只有一部分转化为岩样的弹性能密度积聚在岩样内部中,会随着卸载释放出来;还有一部分以损伤和塑性变形的形式被耗散掉了,耗散掉的能量密度并不会在卸载时释放出来。而加载曲线下的面积为岩样吸收的总能量密度,卸载曲线下的面积为岩石在卸载时释放的弹性能密度,因此卸载曲线在加载曲线的下方,而两者之间的面积即是耗散能密度。

图2 3 种岩石试样的单轴分级加卸载应力-应变曲线图Fig.2 Uniaxial step loading and unloading stress-strain curves of three rock specimens
2.2 单轴压缩试验结果
3 种岩石的单轴压缩应力-应变曲线如图3。
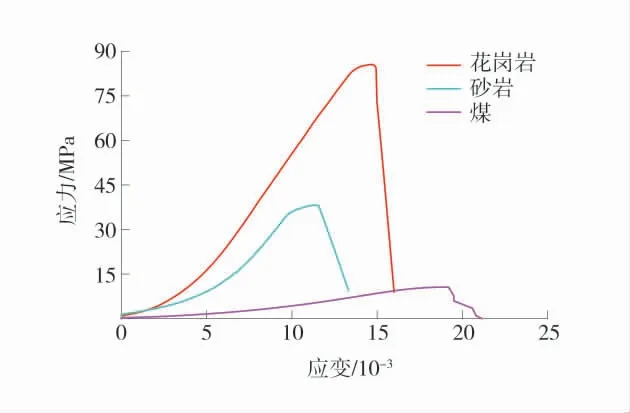
图3 3 种岩石试样单轴压缩应力-应变曲线Fig.3 Uniaxial compression stress-strain curves of three rock specimens
由图3 可知:花岗岩的单轴抗压强度最高,砂岩的单轴抗压强度次之,煤的单轴抗压强度最低,但这3 种岩石在单轴压缩下的应力-应变曲线都具有压缩阶段、弹性阶段、塑性阶段和破坏阶段。由于天然岩石中存在各种孔隙和裂隙,在压密阶段随着荷载的不断增大,岩石内部的孔隙和裂隙不断被压密,宏观上表现为弹性模量不断增大,即应力-应变曲线斜率不断增大;在弹性阶段,岩石的应力与应变近似为线性关系,此时岩石近似可以看作1 个弹性体;在塑性阶段,随着荷载的不断增大,原始裂纹扩展、新的裂隙萌生扩展,不同的孔隙和裂隙渐渐贯通,应力-应变曲线呈现出内凹形式;达到岩石的应力峰值后,岩石会出现宏观破坏,应力-应变曲线开始下降,此时是岩石的破坏阶段。
2.3 单轴压缩与单轴分级加卸载曲线对比
单轴压缩与单轴分级加卸载应力-应变对比曲线如图4。

图4 3 种岩石试样的单轴压缩与单轴分级加卸载应力-应变对比曲线图Fig.4 Comparison curves of uniaxial compression and uniaxial step loading and unloading stress-strain for three kinds of rock samples
由图4 可知:这3 种岩样的单轴分级加卸载应力-应变曲线的外包络线和其单轴压缩应力-应变曲线具有相同的特征—大致,可分为4 个阶段:压密阶段、弹性阶段、塑性阶段以及破坏阶段;但单轴压缩下花岗岩的峰值应力为85.55 MPa,砂岩为38.22 MPa,煤为10.60 MPa;而单轴分级加卸载下花岗岩的峰值应力为87.19 MPa,砂岩为40.75 MPa,煤为11.12 MPa;由此可以看出,单轴压缩的峰值应力要小于单轴分级加卸载的峰值应力,即单轴分级加卸载会使岩石试样强度升高;岩石试样在加卸载过程中,其内部部分接触点会发生应力集中现象,产生较大的应变甚至发生局部破坏,此时产生的碎屑在卸载过程中可能脱落并填充到周围的空隙中,增加了空隙间的界面摩擦,从而提高岩石的强度,即岩石发生硬化现象。
对比图4 中单轴压缩与单轴分级加卸载应力-应变曲线可知:单轴压缩曲线可近似为分级加卸载曲线各卸载点的外包络线,且分级加载次数越小越近似;随着分级加卸载次数的增多,各分级加载产生的损伤和塑性变形积累得越来越多,致使分级加卸载曲线越来越向右移动,使得卸载点与单轴压缩曲线产生了一定的偏离。将最后1 个卸载点处2 条曲线的应变差值与该卸载点应力水平相同处单轴压缩曲线应变值的比值作为评判偏离程度的依据。不同岩石的偏离程度指标见表1。

表1 不同岩石的偏离程度指标Table 1 Deviation degree indexes of different rocks
由表1 可知:煤的偏离程度最大,砂岩的偏离程度次之,花岗岩的偏离程度最小,因此可以认为密实度越大的岩石,其单轴压缩与单轴分级加卸载各卸载点外包络线的偏离程度越小。
3 受载岩石内能量
岩石在受荷载作用下发生变形破坏的过程中,一直伴随着能量的变化:能量输入、能量积聚、能量耗散和能量释放。假设试验过程中没有与外界发生热交换,即向岩石输入的能量只以耗散能和弹性能的形式存在于岩石内部,由能量守恒定律可知,岩石的能量公式为[19]:
式中:u 为岩石吸收的总能量密度;ud为耗散能密度;ue为弹性能密度。
3.1 分级加卸载峰前能量
从众多循环加卸载的研究[20-24]中可以看出,循环次数对卸载曲线的演化趋势影响较小,且刘之喜等[18]研究中发现循环次数对弹性能影响较小,因此可以认为单轴分级加卸载的卸载点处弹性能等于荷载相等时单轴压缩的弹性能。分级加卸载峰前能量示意图如图5。

图5 分级加卸载峰前能量示意图Fig.5 Schematic diagram of pre-peak energy of step loading and unloading
根据岩石应力-应变曲线的特征可知,加载曲线以下的面积表示外界对岩石输入的总能量密度,卸载曲线以下的面积表示卸载过程中释放的弹性能密度,加载曲线、卸载曲线及应变轴之间的面积表示岩石的耗散能密度。各能量的具体计算方法为:
式中:ue为岩石试样在应力水平σ 下的弹性能密度;ud为岩石试样在应力水平σ 下的耗散能密度;ε2为σ 对应的应变值;ε1为应力由σ 降低至0时对应的参与应变值。
3.2 分级加卸载峰后能量
由于峰后阶段并无加载曲线和卸载曲线,因此并不能用上述方法计算峰后的弹性能密度,这时可以采用公式法计算。分级加卸载峰后能量示意图如图6。

图6 分级加卸载峰后能量示意图Fig.6 Schematic diagram of post-peak energy of step loading and unloading
在主应力空间中岩体单元弹性能密度为:
式中:ue为岩石试样单元弹性能密度;σi(i=1,2,3)为岩石试样三向主应力;εie(i=1,2,3)为σi对应的应变值。
利用胡克定理将式(4)改写为:
式中:E0为初始弹性模量;ν 为泊松比。
单轴压缩试验弹性能密度计算公式可简化为:
4 岩石的能量演化
4.1 单轴分级加卸载下岩石的能量演化规律
根据3 种岩石试样的单轴分级加卸载应力-应变曲线,采用上述岩石能量的计算方法可以得到岩石的输入总能量密度、弹性能密度及耗散能密度。
4.1.1 加卸载条件下峰前能量演化
3 种岩石试样分级加卸载条件下的峰前能量演化曲线如图7。

图7 3 种岩石试样分级加卸载条件下的峰前能量演化曲线Fig.7 Pre-peak energy evolution curves of three rock specimens under step loading and unloading conditions
由图7 可知:在峰前阶段,3 种岩石试样的能量演化特征相似,每种岩石试样的3 条能量密度曲线都呈现出一直增大的趋势,且随着应力水平的不断增加,其增加的速率不断变大;从整体上看,3 种岩石试样的弹性能密度在峰前阶段基本上大于耗散能密度;峰前阶段花岗岩、砂岩和煤的弹性能密度最大值分别为0.293、0.065、0.04 mJ/mm,即花岗岩弹性能密度极限值最大,砂岩弹性能密度次之,煤弹性能密度最小,这说明强度越大的岩石,其弹性能密度极限值越大,即其能储存的弹性能越大,破坏时释放出的能量越大。
4.1.2 加卸载条件下峰后能量演化
3 种岩石试样分级加卸载条件下的峰后能量演化曲线如图8。
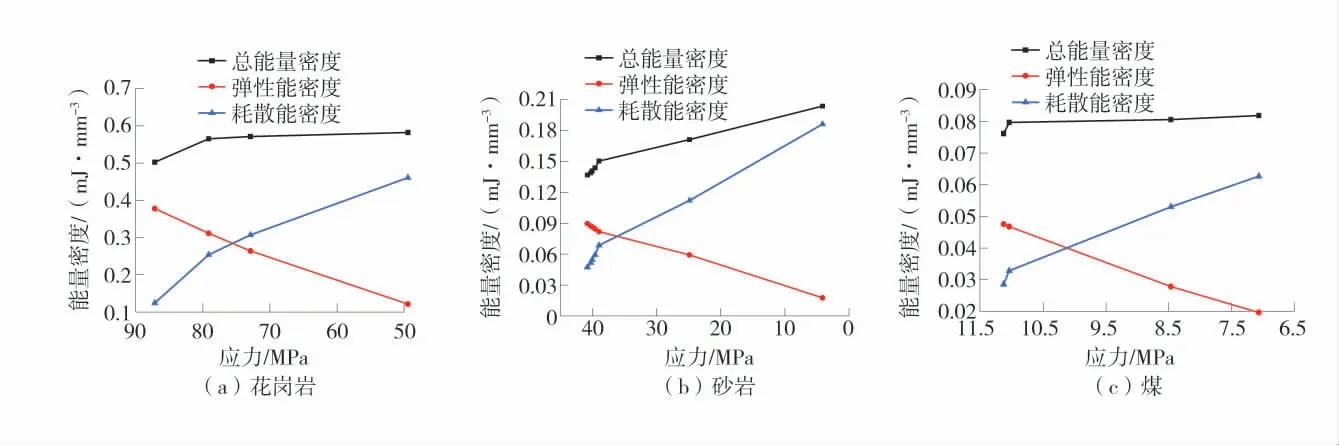
图8 3 种岩石试样分级加卸载条件下的峰后能量演化曲线Fig.8 Post-peak energy evolution curves of three rock specimens under step loading and unloading conditions
由图8 可知:在峰后阶段,3 种岩石的能量演化特征也相似,总能量密度曲线一直增大,但在岩石试样破坏的瞬间突然增大,之后增加速率减小;弹性能密度曲线大幅减小,且呈近似线性变化,说明岩石试样在发生破坏时,储存在其内部的弹性能瞬间被释放出来,宏观上以碎屑的动能,裂纹表面的摩擦能及音波等形式迅速释放。
4.2 单轴压缩条件下岩石的能量演化规律
根据上述能量计算方法及单轴压缩条件下的应力-应变曲线,可以得3 种岩石试样单轴压缩条件下的输入总能量密度、弹性能密度及耗散能密度。
4.2.1 单轴压缩条件下峰前能量演化
3 种岩石试样单轴压缩条件下峰前能量演化曲线如图9。

图9 3 种岩石试样单轴压缩条件下峰前能量演化曲线Fig.9 Pre-peak energy evolution curves of three kinds of rock samples under uniaxial compression
由图9 可知:3 种岩石试样在单轴压缩条件下的能量演化特征和在单轴分级加卸载条件下的能量演化特征相似,在峰前阶段,3 条能量密度曲线整体仍呈现出增大的趋势,且整体呈现出非线性特征,开始增加速度缓慢,后期加快;单轴压缩条件下花岗岩弹性能密度极限值仍最大,砂岩弹性能密度次之,煤弹性能密度最小。
4.2.2 单轴压缩条件下峰后能量演化
3 种岩石试样单轴压缩条件下峰后能量演化曲线如图10。
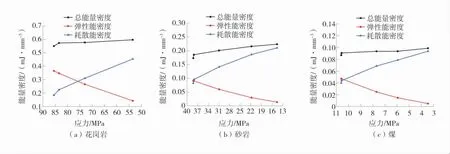
图10 3 种岩石试样单轴压缩条件下峰后能量演化曲线Fig.10 Post-peak energy evolution curves of three kinds of rock samples under uniaxial compression
由图10 可知:与在单轴分级加卸载条件下的峰后能量演化曲线相似,单轴压缩下总能量密度整体呈现缓慢的上升趋势,但在岩石试样破坏瞬间,其应变的突然增大,导致了总能量密度突然增加;弹性能密度大幅减小且呈近似线性变化。
4.3 不同岩石能量对比
3 种岩石不同条件下能量分配规律对比如图11。
由图11 可知:3 种岩石试样能量分配规律相似,单轴压缩和分级加卸载条件下总能量密度都一直增大,但前者增加速率大于后者增加速率,临近破坏时两者相差最大,说明各分级加载产生的损伤和塑性变形是不可逆的,下个分级加载未达到上一卸载点应力水平时,其产生的耗散能密度较小,从而单轴总能量密度大于分级总能量密度;由于弹性能密度相等,耗散能密度与总能量密度规律相同。

图11 3 种岩石不同条件下能量分配规律对比图Fig.11 Contrast of the energy distribution laws of three kinds of rock specimens under different conditions
5 岩石线性储能规律
单轴压缩和单轴分级加卸载下岩石能量演化规律相似。下面主要探究单轴压缩和单轴分级加卸载峰值强度处弹性能密度之间的关系。宫凤强等[16,25]根据一次加卸载不会改变岩石试样单轴压缩整体受力情况,设定不同应力水平下的单轴一次加卸载试验,研究结果表明,单轴压缩下弹性能密度与总能量密度呈线性关系。
单轴压缩和单轴分级加卸载不同应力水平下弹性能密度和总能量密度的拟合图如图12 和图13。

图12 单轴压缩下弹性能密度-总能量密度拟合曲线Fig.12 Elastic energy density-total energy density fitting curves under uniaxial compression

图13 单轴分级加卸载下弹性能密度-总能量密度拟合曲线Fig.13 Elastic energy density-total energy density fitting curves under single-axis graded loading and unloading
由图12 和图13 可知:3 种岩石试样的弹性能密度和总能量密度不仅在单轴压缩下满足线性函数ue=au+b 关系,在单轴分级加卸载下同样满足,且线性函数的相关系数R2均大于0.995,表明弹性能密度与总能量密度之间的线性关系较强。
根据应力-应变曲线及上述的能量计算方法可以得到每个岩石试样在峰值强度处的总能量密度,将该值代入拟合函数中,即可得到不同岩石在单轴压缩和单轴分级加卸载下峰值强度处的弹性能密度,岩石试样峰值能量密度计算结果见表2。

表2 岩石试样峰值能量密度计算结果Tab.2 Calculation results of peak energy density of rock specimens
由表2 可以看出:花岗岩峰值强度处的弹性能密度最大,砂岩次之,煤最小,这说明强度越大的岩石,其储能极限越大。3 种岩石试样在单轴压缩和单轴分级加卸载下峰值强度处的弹性能密度几乎相等,绝对误差不大于1%,说明单轴分级加卸载相对于单轴压缩仅能改变峰值强度处的总能量密度,而不能改变弹性能密度。因此可以利用单轴分级加卸载计算单轴压缩峰值处的弹性能密度,得到一种计算岩石储能极限的新方法。
6 结 语
1)单轴分级加卸载应力-应变曲线的外包络线和其单轴压缩应力-应变曲线具有相同趋势,随着分级加卸载次数的增多,各卸载点与单轴压缩曲线产生了一定的偏离,且密度越大的岩石,其单轴分级加卸载与单轴压缩曲线的偏离程度越小。
2)岩石并非均质体,加载过程中,其局部存在应力集中现象,会产生较大的应变甚至发生局部破坏,卸载时应力集中形成碎屑可能脱落并填充到周围的裂隙中,增加裂纹间摩擦力,提高岩石承载能力提升。
3)3 种岩石试样的弹性能密度和总能量密度在单轴压缩与单轴分级加卸载下均满足线性储能规律,且单轴压缩和单轴分级加卸载下峰值强度处的弹性能密度几乎相等。
4)利用线性储能规律得到了岩石单轴分级加卸载与单轴压缩储能极限,并且岩石储能极限与强度存在正相关性,即强度越大岩石的储能极限越大。

