多主桁钢桁梁桥桥面荷载横向分配计算方法研究

韩衍群，侯文崎

(1.中南大学 土木工程学院，湖南 长沙，410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙，410075)

随着我国国民经济的快速发展，为了满足运输需求，要求桥梁越来越宽。为减小构件规模、降低制造成本，钢桁梁桥越来越多采用三主桁或多主桁结构形式[1-5]，如武汉天兴洲长江大桥、南京大胜关长江大桥均采用多主桁结构形式。

从力学上讲，多主桁结构与两主桁相比，其最大差别是桥面荷载在主桁间分配的不均匀性[6-7]。在两主桁结构中，均布桥面荷载在横桥向是等分的。但在多主桁结构中，桥面荷载在主桁间的分配比较复杂[8]。以三主桁结构为例，若不考虑两边桁下弦节点刚性，则桥面荷载在三主桁间下弦节点上分配的力学模型相当于带支座沉降的两跨连续梁，若主桁间竖向位移相同，则在均布荷载作用下，中桁与边桁分配的荷载比为10:3。实际上，由于中桁挠度比边桁的大，桥面荷载在中桁与边桁分配小于10:3。另外，由于横联的作用，使主桁的力从挠度较大的中桁转移到挠度较小的边桁，从而使中桁与边桁的受力差别减小。桥面荷载在主桁间分配的不均匀性将导致主桁间结构内力存在差异，若差异较大，为了结构安全，常采用增大中桁构件截面的办法来解决，但该方法增加节点与杆件种类，不便于预制与拼装。目前，国内有些学者对三主桁受力不均匀性进行了研究[9-11]，而国外对这方面的研究很少。刘世忠等[12]通过支座升降技术对内力进行调整，研究了减小受力不均匀性的方法；鲍莉霞[13]采用空间有限元从结构布置角度研究了设置横联与否对三主桁结构内力分配的影响，但没有研究主桁刚度对内力分配的影响，也没有给出合理刚度；候文崎等[14-16]对三主桁受力特性进行了试验研究，给出了减小受力差别的一些建议，但对荷载横向传递规律和计算方法研究较少。目前，对二主桁中结构桥面荷载横向分配计算有可靠的计算公式，而多主桁桥面荷载横向分配比二主桁复杂得多，对这类桥梁常采用空间有限元法进行分析计算[17-18]。空间有限元法虽然计算精度高，但建模复杂，费时费力，在桥梁设计初期或方案比选时并不是很好的选择。本文以三主桁钢桁梁桥为例，从桥面荷载横向传递路径入手，研究横向分配的简化计算模型，并基于能量原理推导桥面荷载横向分配的计算公式。在此基础上，利用结构设计不同参数研究主桁间横向分配不均匀的影响因素，提出合理刚度取值，以便为该类桥梁简化计算提供依据。

1 桥面荷载横桥向二次分配

将桥面荷载在下弦节点间的分配称为第一次分配[20-21]。由于存在三主桁间挠度差，桥面荷载再通过横联在3 片主桁间重分配，称为第二次分配。第一次分配的桥面荷载作用于主桁的下弦节点，而第二次分配的力作用于上弦节点。在实际桥梁中，2次分配是相互关联、相互影响的，并不是第一次分配完后再进行第二次分配，而是2次分配同时进行，为了叙述方便，下面分别考察2次分配的情况。

1.1 桥面荷载横桥向第一次分配

若不考虑两边桁下弦杆节点刚性，即横梁与两边桁下弦节点铰接连接，则横梁的受力相当于1个两跨连续梁，其力学模型如图1(a)所示，支座反力即为分配到每片主桁的荷载。三主桁在桥面荷载作用下，以作用均布荷载q为例，由于受力的不均匀性，三主桁竖向存在挠度差，相当于在图1(a)中的中支座处有一沉降Δ。将图1(a)中的受力状态分解为主桁无竖向位移(图1(b))和主桁有竖向位移(图1(c))。图1(b)中只有荷载无支座沉降，而图1(c)中只有支座沉降无荷载。由结构力学知识可知：图1(b)中的端支座和中支座反力分别为二者之比为3:10。当图1(c)中支座产生沉降Δ时，中支座有向下反力而两端铰支座的支反力为(其中，E和Ih分别为钢的弹性模量和横梁的惯性矩(包括桥面板))。由此可见，由于支座沉降，图1(a)中支座反力释放了一部分，而两端的支座反力增加。

在实际桥梁中，下弦节点对横梁端部的转动有一定的约束作用，相当于图1中两跨连续梁两端支座并不是理想的铰支座，而是能够承受一定弯矩的弹性支座，这样，端支座和中支座之间的反力差又减小了一部分。图1(a)中的3 个支座反力相当于横桥向3 片主桁下弦节点(下弦杆)对横梁的支承力，在数值上等于3片主桁下弦节点上分配的桥面荷载，将其称为桥面荷载的第一次分配。各主桁分配的桥面荷载的比例既与横梁的线刚度有关，也与三片桁的挠度差Δ有关。

图1 横梁受力分解示意图Fig.1 Mechanical behavior decomposition of transverse beams

1.2 桥面荷载横桥向第二次分配

3片主桁第一次分配到桥面荷载差别较大，中桁的荷载大，边桁的荷载小，从而中桁的挠度大于边桁的挠度。而上部横联将3 片主桁联成一体，抵抗3片主桁间的挠度差，从而产生了桥面荷载横桥向的第二次分配。

为分析桥面荷载在横桥向的第二次分配，在主桁节点处横桥向取出1个横联作为隔离体，横联上3 个弹簧表示3 片主桁对横联的支撑，如图2所示。与横梁受力类似，横联在3片主桁挠度差Δ下将产生支反力，其大小在边桁处为，在中桁处为(其中，Ieq为横联等效惯性矩)。该反力即横联对主桁的作用力与横联竖向刚度和三主桁的挠度差有关。横联竖向刚度、三主桁间的挠度差越大，横联对主桁的作用力越大。

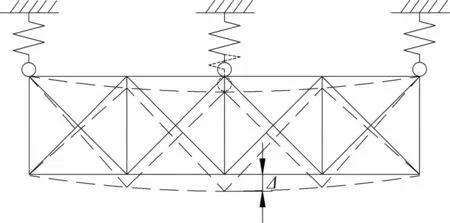
图2 横联受力示意图Fig.2 Mechanical behavior of lateral bracings

2 桥面荷载横向分配的简化模型及计算公式

2.1 桥面荷载横向分配简化模型

为分析桥面荷载在横桥向的二次分配，在主桁节点处横桥向取出1 个框架作为隔离体，如图3(a)所示。图3中，q(x)为桥面荷载，l为桁宽，横向框架上、下各用3个弹簧表示3片主桁对框架的支撑。每片桁架上下弹簧刚度之和为代表框架所在位置处主桁的竖向刚度，其中，i为下弦节点号，j为桁号，分别为框架在上、下位置主桁的竖向刚度，kij为框架所在位置主桁的总竖向刚度。

kij可按如下方法计算：取第j片主桁，在每个下弦节点作用单位荷载P=1 kN，引起第i个下弦节点竖向挠度为Δij，则定义该节点处弹簧刚度kij=1/Δij。因为不影响桥面荷载的第一、第二次分配[7]，为简化计算，令相等，均为kij的1/2。

图3(b)所示为竖杆、横联、横梁的隔离体图。图中，竖杆下部所受的力为第一次分配的力，上部所受的力为第二次分配的力。由图3(b)可见：3片主桁间的横联将挠度较大的中桁向上提，而将边桁向下压，使主桁上、下节点所受竖向力总和在3片主桁间的差距减小。

图3 横向框架简化计算模型Fig.3 Simplified calculation model of transverse frame

2.2 计算公式推导

假设：

1)不考虑腹杆轴向变形对三主桁竖向挠度差的影响；

2)两边桁的杆件截面相同，即竖向刚度相同；

3)不考虑腹杆、下弦杆对横梁转动约束的作用；

4)主桁间的桁宽相同。

在桥面荷载作用下，三主桁钢桁梁桥的受力可分解为如图4所示的两部分：

图4 三主桁钢桁梁桥受力分解Fig.4 Dissociation of mechanical behavior of three-main-truss steel bridges

① 横联刚度无限大，即3 片主桁没有竖向挠度差；

② 在①变形的基础上，横联刚度由无限刚度变到实际刚度，此时，3 片主桁发生竖向挠度差Δi。

在对称荷载作用下，在状态②中，设中桁与边桁的竖向挠度差为Δi，可得出边桁处弹簧变形为

式中：Ih为横梁(包括桥面板)惯性矩；Ieq为横联等效惯性矩；l为主桁间的桁宽。由于两边桁相同，因此，两边桁处弹簧变形相同。

以①的位置为初始位置，②中横梁(横联)的挠度方程为

坐标原点在横梁(横联)最左端，y以向上为正。

则在②中，横梁的变形能为

横联的变形能为

弹簧的变形能为

将式(1)代入式(5)得

外力势能为

式中：q(x)为外荷载，向上为正。横向框架总势能为

式中：Π1为①的总势能，其与Δi无关；Π2=Uh+Uhl+Ut-V，为②的总势能，为Δi的函数。由最小势能原理得

将式(3)，(4)和(6)代入式(10)得

第一次分配到3片主桁的荷载为

第二次分配到3片主桁的荷载为

分配到每片主桁上的总荷载为

当受偏载作用时，可将荷载分解为对称荷载与反对称荷载的叠加，对称荷载下的横向分配可按式(14)计算。在反对称荷载作用下，根据对称结构的受力特性可知，桥面荷载全部分配到两边桁上，中桁不分配荷载，即

则偏载作用下分配到每片主桁上的总荷载为

由式(11)和(14)可以看出，当主桁竖向刚度越大即ki越大时，Δi就越小，则分配到边桁的荷载越少，分配到中桁的荷载就越多；相反，当主桁竖向刚度越小即ki越小时，Δi就越大，则分配到边桁与中桁上的荷载越接近。因此，越靠近支座处，分配到边桁与中桁上的荷载差值越大；越靠近跨中，分配到边桁与中桁上的荷载越接近。横向联系(包括横联、横梁、桥面板)竖向刚度越大，三主桁间分配的荷载越接近，因此，横向联系具有合适的竖向刚度是减小主桁间受力不均匀的关键。在实际桥梁中，横联竖向刚度一般比横梁(包括桥面板)刚度大很多，因此，横联竖向刚度是影响桥面荷载横向分配的主要因素之一[7]。

3 算例验证

以某(84+84)m两跨连续三主桁钢桁梁桥为例，节间长度为12 m，N 型桁架，桥面横桥向宽度为(15+15)m，如图5所示。该桥三主桁各杆件截面基本相同，即三主桁刚度相同。建立该桥空间有限元模型，保持杆件布置不变，分别改变主桁竖向刚度、横联竖向刚度计算出在对称均布荷载作用下靠近跨中节点位置桥面荷载在三主桁间的分配，同时，用公式计算结果与其对比，计算结果见表1和表2。

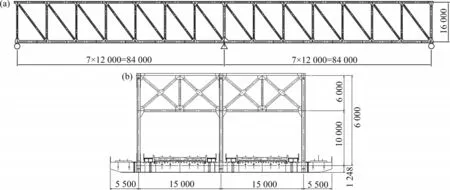
图5 三主桁钢桁梁桥Fig.5 Structure diagram of the three-main-truss steel bridge

表1 和表2 中：γ1和γ2分别为一片主桁第一次分配、第二次分配的桥面荷载与三主桁2次分配总荷载的比。由于两边桁计算结果相同，故边桁的γ1和γ2与中桁的γ1和γ2存在如下关系：

表1和表2中计算结果仅列出了中桁的计算结果，其中，不均匀度系数。

由表1可见：公式计算得到的桥面荷载在三主桁间第一次分配γ1、第二次分配γ2和2次分配后的计算结果均与空间计算结果较吻合，验证了公式的正确性；随着弹簧刚度增加，三主桁竖向挠度差减小，中桁γ1有所增加，中桁γ2逐渐减少。由于横联竖向刚度比横梁竖向刚度大，因此，中桁γ2减少速度大于中桁γ1增加速度，经二次分配后，荷载不均匀度系数α逐渐增加；当弹簧刚度趋于无限大时(即支座处)，α趋于10:3，靠近跨中逐渐减小；当主桁刚度在3.90×104kN/m 以下时，α不超过1.17，即中桁承受的荷载与边桁差别不大。

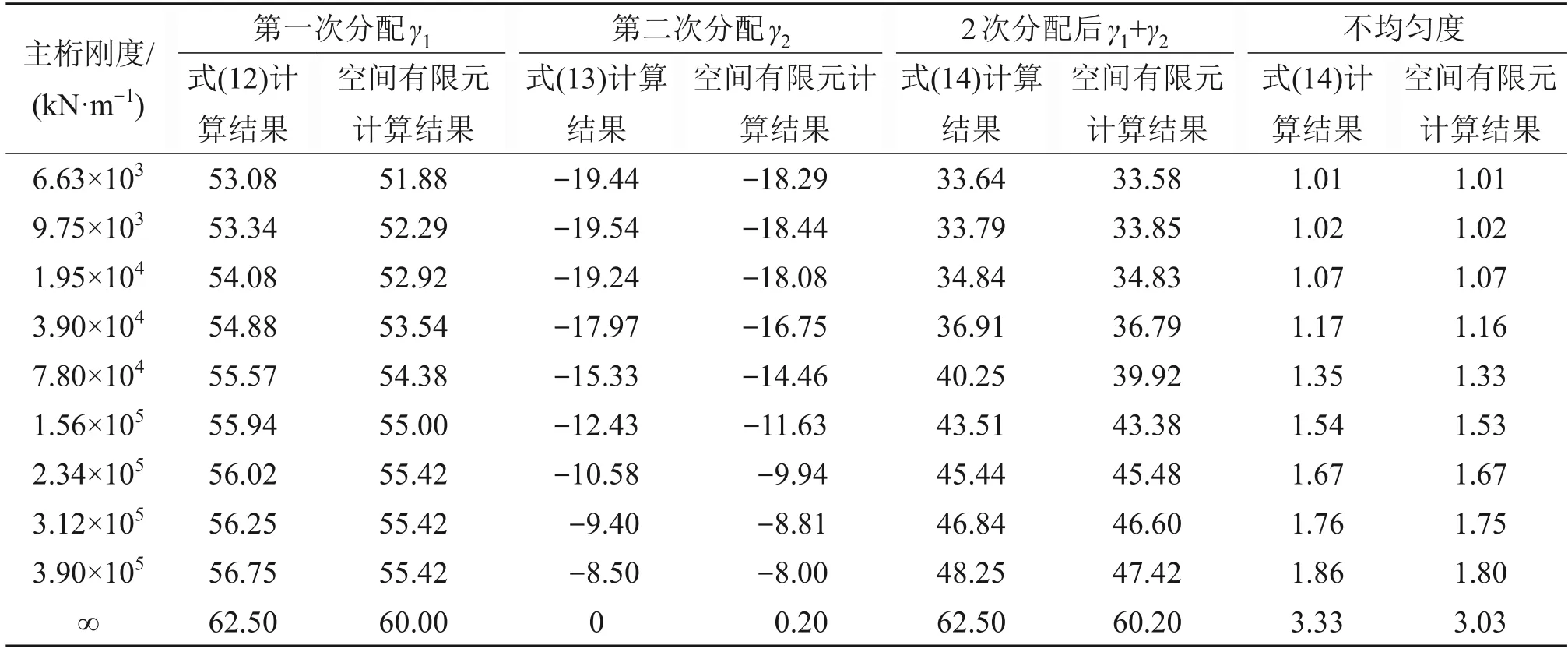
表1 不同弹簧刚度下中桁横向分配公式计算结果与空间有限元计算结果对比Table 1 Comparison of calculation results of middle truss transverse distribution load formula and spatial finite element results under different spring stiffness

横联竖向刚度用其跨中产生单位位移所需的力表示，如图6所示。图6中，l为主桁宽度，kh为横联竖向刚度。由表2可见：中桁的γ1和γ2随横联竖向刚度的增加而增加，且γ1和γ2增加速度随横联竖向刚度的增加逐渐减小；当横联竖向刚度在1.5×105kN/m以下变化时，γ2增加的速度较快；当横联竖向刚度大于3.0×105kN/m时，γ2增加的速度较缓慢，因此，横联竖向刚度在1.5×105～3.0×105kN/m范围内比较合理。

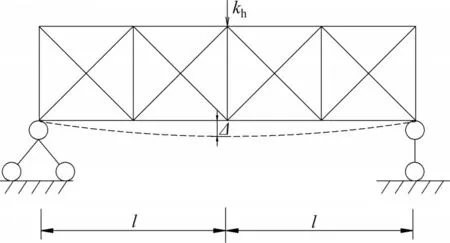
图6 横联竖向刚度示意图Fig.6 Diagrammatic sketch of vertical stiffness of lateral bracings

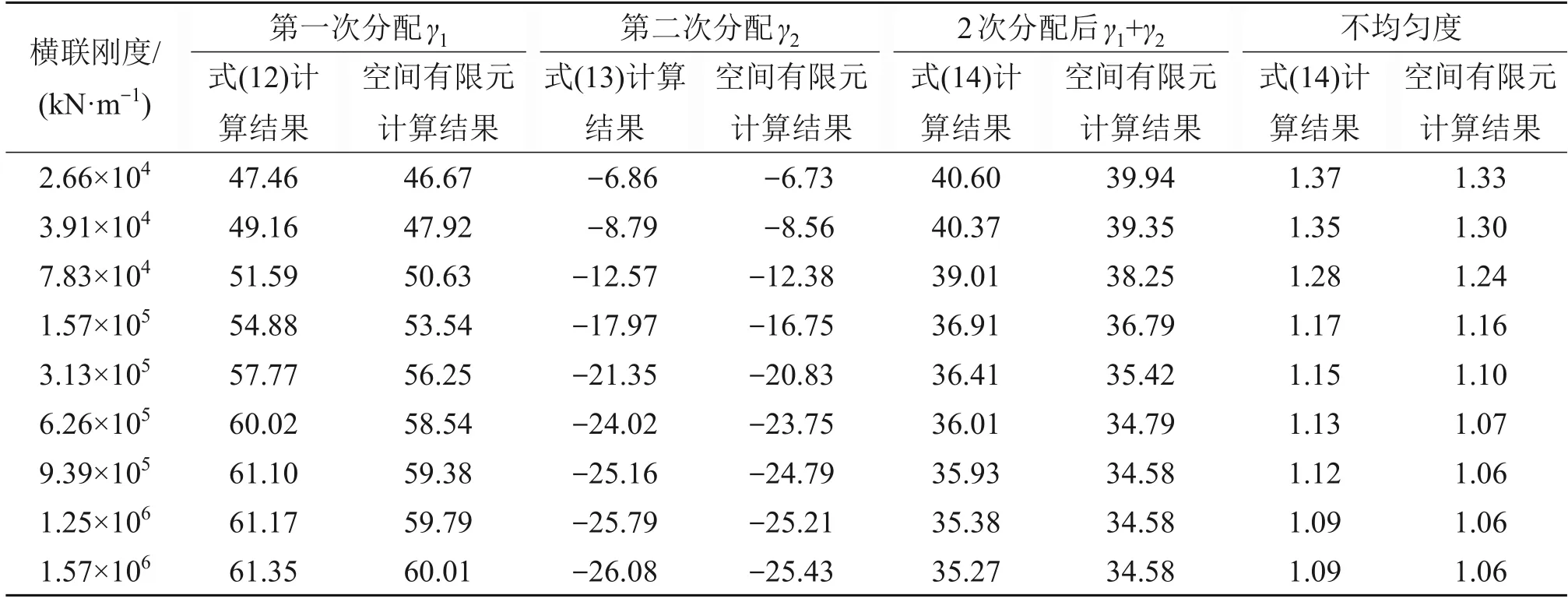
表2 不同横联刚度下中桁横向分配公式计算结果与空间有限元计算结果对比Table 2 Comparison of calculation results of middle truss transverse distribution load formula and spatial finite element results under different lateral bracings stiffness

对该桥6 节间缩尺比例为1:6 的试验模型两端简支在试验荷载(对称荷载)作用下，采用横向分配计算公式计算分配到每片主桁的荷载，对每片主桁单独计算(以下将该法称为PF 法)，计算每片主桁的挠度和各杆件应力，并将计算结果与空间有限元计算结果和试验值进行对比，见图7～9(两边桁计算结果相同，故图7～9仅列出一边桁的计算结果，坐标原点位于梁的一端)。

图7 下弦杆竖向挠度Fig.7 Ⅴertical deflection of bottom chords

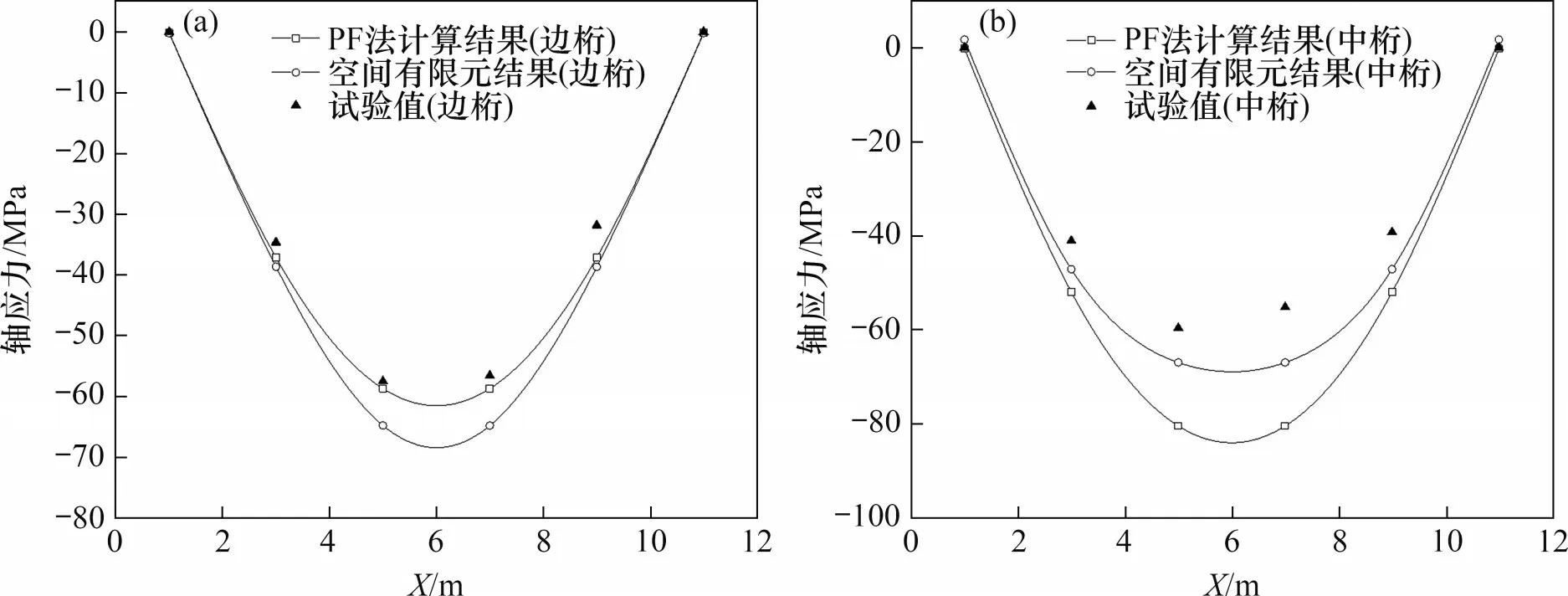
图8 上弦杆轴应力Fig.8 Axial stress of top chords

图9 斜杆轴应力Fig.9 Axial stress of diagonal bar

由图7～9 可见：采用PF 法所得边桁、中桁挠度计算结果与空间有限元计算结果、试验值较接近，挠度最大相对误差在7.3%之内，采用PF法所得边桁、中桁杆件应力计算结果与空间有限元计算结果、试验值(除上弦杆中桁外)较接近，应力最大相对误差在9.4%以内，与空间有限元计算结果和试验值相比，PF 法所得计算结果中，中桁的偏大，边桁的偏小。这是由于在实际桥梁中，边桁下弦节点对横梁的转动约束作用大于横向框架简化模型对横梁的转动约束作用，导致采用式(14)计算的桥面荷载横向分配中，边桁的偏小，中桁的偏大，但在桥梁初步设计或方案比选时，公式计算精度可满足要求。由此可见，由PF 法计算结果与空间有限元计算结果、试验值均较吻合，说明按照横向分配计算公式计算每片主桁分配的荷载接近实际情况，验证了公式的正确性，确定出桥面荷载横向分配后，多主桁结构可按平面结构进行简化计算。

4 结论

1)利用式(14)对三主桁桥面荷载横向分配计算时，所得结果与空间有限元计算结果、试验值均较吻合，验证了公式的正确性。

2)桥面荷载在三主桁间横向分配主要受主桁、横联竖向刚度影响。在均布对称荷载作用下，不均匀度系数α随主桁竖向刚度增加而增加，在支座处较大，为3.33，靠近跨中逐渐减小。当主桁竖向刚度在3.9×104kN/m 以下时，α不大于1.17；α随横联竖向刚度的增加而减小，横联竖向刚度在1.5×105～3.0×105kN/m范围内较合理。

3)确定桥面荷载横向分配后，多主桁结构可按平面结构简化计算。