韧性视角下基于随机演变的城市应急医疗物资配置模型

李智楠，刘勤明，陆昊洋

（上海理工大学 管理学院，上海 200093）

0 引言

随着我国城镇化的不断推进，越来越多的人口向城市聚集。由于人口密度高、流动性大，突发公共卫生事件考验着城市的应急管理能力。在突发公共卫生事件处置过程中，对于应急医疗物资（如口罩、防护服、医用酒精等）的需求非常大，短时供需关系极不平衡。对于城市应急医疗物资的配置，既要满足伤患的医疗需求，保证伤患得到有效治疗，又要起到阻止突发公共卫生事件扩散的作用。因此，如何提升城市应对突发公共卫生事件的能力，是必须要面对的重大课题。

韧性的概念最早来源于物理学，随着韧性理念不断运用到各个领域，它被定义为“在遇到不确定干扰时，系统能够消化、吸收干扰并能保持原来结构，维持关键功能的能力”。卫生系统韧性的概念已经在全球卫生领域得到普及，大量出现在联合国政策、学术和会议文章［1］中。Sochas等［2］在埃博拉病毒暴发的背景下，运用健康管理系统的数据分析了塞拉利昂的卫生系统韧性；Bhandari等［3］基于社区韧性层面，建立了公共卫生系统韧性的指标体系，但对不同地区的韧性缺乏比较。国外文献［2-4］的研究主要集中在第三世界国家的卫生系统韧性，缺乏对我国实际情况的考虑。在面向地震情景的卫生系统韧性评估中，尚庆学等［5］构建了一种量化医疗系统抗震韧性的评价体系；费智涛等［6］研究了复杂网络下城市卫生系统韧性，从韧性的健壮性、冗杂性、多样性和快速性构建评估指标，并对地震情景下北京六环内区域进行评估。但是，地震与突发公共卫生事件在韧性评估体系上有较大区别，因此适用性仍需验证。面向突发公共卫生事件的韧性评估，李寻昌等［7］针对韧性的“吸收能力、恢复能力、适应能力”三个评价维度，结合直觉模糊集解法TOPSIS（Technique for Order Preference by Similarity to an Ideal Solution）对中日韩等六个国家进行韧性评估，但是国家层面的评价指标并不适用于城市辖区的评估；林钰涵等［8］基于韧性城市理论建立了城市卫生系统韧性的评价体系，但仅对一维的评价结果采用自然间断点进行分类，没有考虑韧性能力的三个评价维度的影响。

对应急医疗物资的配置研究中，大量学者取得了诸多成果。胡晓伟等［9］根据应急医疗物资的供需变化特点，分别以需求满足率、就近运输原则为主次目标建立模型；张国富等［10］对于化工园区应急物资的配置问题，以应急响应的时效性和物资消耗的连续性建立多目标配置模型；严华健等［11］建立了综合考虑响应时间及成本、灾民恐慌度及损失、救灾物资未满足度及分配公平性的高维多目标优化模型。以上模型主要考虑了单一阶段的情形，而突发事件下需要考虑多阶段的配置问题，应急物资配置问题也从确定条件转向不确定条件［12］。李珍萍等［13］和Zhang等［14］考虑了储备与配置两阶段的联合优化，但是并未考虑到配置的多阶段性；李艳等［15］构建了患者恐慌心理函数，并以患者恐慌情绪和配置总成本最小化为目标建立多周期配置模型；段容谷等［16］以需求未满足损失最小化及物资分配总距离最小化为目标，建立多阶段物资配置模型；葛洪磊等［17］基于重大传染病疫情演化情境，构建了多阶段贝叶斯序贯决策模型。然而上述多阶段配置研究并未考虑到随事件演变导致需求多阶段动态演变的实际情况。

已有许多研究将马尔可夫（Markov）链用于描述突发事件的随机性、动态性等特征。例如刘阳等［18］将突发事件的状态转移过程设计成齐次Markov 链，结合数量柔性契约设计应急物资采购模型；Keneally等［19］研究了作战环境中的空军医疗派遣策略，用Markov 决策来解决复杂的空中医疗资源分配问题；张晓楠等［20］考虑多车辆情况下以总运输成本最小化为目标，建立基于随机需求演变的Markov 决策模型；李飞飞等［21］在分布式多项目随机调度下，建立各项目调度的Markov 动态决策模型。对于事态不断演变的突发卫生事件，应用Markov 链构建动态多阶段配置模型，可以建立多阶段应急医疗物资动态配置模型。

本文面向突发公共卫生事件，建立城市卫生系统韧性评估模型，并运用K-means 算法对辖区韧性差异从吸收能力、适应能力和恢复能力进行评级；依据城市突发公共卫生事件的特点，将应急物资需求的随机演变过程设计成Markov 过程，并结合韧性建立多阶段动态配置模型；最后，采用二进制人工蜂群（Artificial Bee Colony，ABC）算法求解模型。

1 问题描述

突发公共卫生事件下，城市应急医疗物资配置的首要目标是在供应有限的前提下，制定合适的配置策略和数量，尽可能缓解各辖区物资短缺的情况。但是，由于疫情不断扩散和需求满足程度的演变，物资需求也不断变化，因此这是一个动态决策的过程。

“需求状态”是辖区对应急医疗物资的需求程度。突发公共卫生事件时，辖区可能正处于不同的需求状态。应急医疗物资的需求状态随事件的演变发生变化，类似于Markov决策过程中系统的演变取决于状态之间的转变。Markov 决策过程是决策者阶段性地观察具有Markov 性质的随机系统做出序贯决策的过程［18］。未来的需求状态随机，它的条件概率分布仅依赖于当前状态，所以该随机过程具有Markov性质。决策者根据观察到的需求状态从可用的配置策略集合中选择一个作出决策，如果未得到配置，需求状态可能会保持原状或者向后演变；如果得到配置，需求状态也可能保持原状或向前演变，如图1 所示。下一阶段，决策者再根据新观察到的需求状态作出决策，并反复进行。

图1 需求状态的演变Fig.1 Evolution of demand state

在突发公共卫生事件的动态演变情形下，Markov 决策过程考虑当前需求状态对未来状态的影响，能够量化地体现需求状态动态演变的趋势。因此，本文将应用Markov 过程对突发公共卫生事件下的应急医疗物资配置问题进行研究。

2 韧性评估模型

根据系统韧性的定义，Vugrin等［22］和Francis等［23］将系统韧性量化为吸收能力、适应能力和的恢复能力的组合。随着研究的深入，基于韧性能力表征的三个重要特征得到了学者们的广泛认可［24-25］。

在面向突发公共卫生事件的卫生系统韧性评估中，吸收能力指系统承受扰动冲击时减少系统损失的能力，主要体现在系统应对事件的脆弱性和应急管理部门的应对能力等；恢复能力指系统恢复正常功能的能力，主要体现在辖区的医疗卫生水平等；适应能力指系统自学习以应对下次扰动的能力，主要体现在辖区的社会发展水平和经济水平等。

辖区卫生系统韧性评估指标分为2 层。准则层指标包括吸收能力Rx、适应能力Rs和恢复能力Rh；指标层指标是反映准则层的影响因子，根据BRIC（Baseline Resilience Indicators for Communities）［26］和卫生系统韧性积分卡，借鉴李寻昌等［7］和林钰涵等［8］构建卫生系统韧性评价指标，共计12 项，如表1 所示。

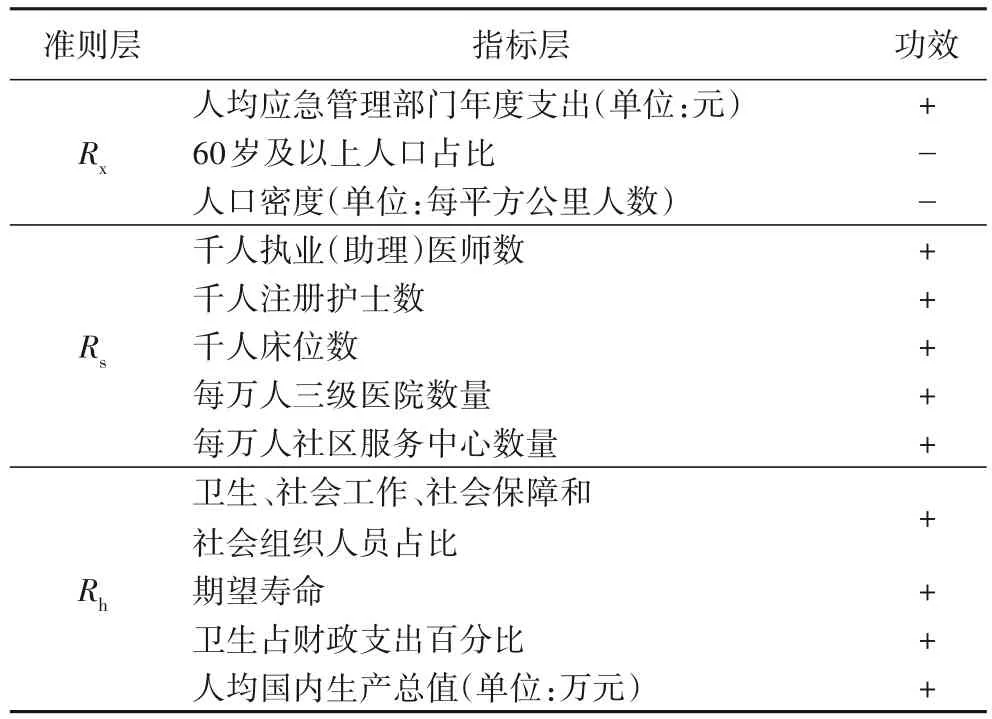
表1 辖区卫生系统韧性评估指标Tab.1 Area’s health system resilience assessment indicators

由于以往研究并未考虑到韧性的三种能力表征对韧性综合评价的不同影响，所以本文采用熵值法建立面向突发公共卫生事件的辖区卫生系统韧性评估模型。熵值法通过计算各指标包含的信息量，确定各指标的权重，能够深刻地反映出指标信息熵值的效用价值［27］。

计算辖区卫生系统韧性的度量值：

1）数据标准化。xij为第i个辖区在第j项的值，由于各指标的量纲不同，所以先对数据进行标准化处理。

2）计算第j项指标所占的比重：

3）计算第j项的信息熵值：

4）计算信息熵的冗杂度：

5）计算各指标的权重：

6）根据以上计算，得出辖区卫生系统韧性评估模型。

根据各辖区韧性能力得分，采用K-means 算法进行聚类分析。对于三维数据，选择欧氏距离进行类别判定［28］：

并对三个类别进行综合评分（Category Comprehensive Score，CCS），形成韧性分类标准：

3 应急物资动态配置模型

当公共卫生事件发生时，城市内各辖区都急需应急医疗物资，需求量往往远大于供应量。在供需关系极不平衡的情况下，某一阶段可分配的应急医疗物资不可能满足所有辖区的需求。因此，本文根据Markov 过程对应急医疗物资的需求状态进行建模，对各辖区动态配置物资。

假设J为辖区的集合，J={j|1，2，…，jmax}；K为应急医疗物资的集合，K={k|1，2，…，kmax}；T为救援阶段的集合，T={t|1，2，…，tmax}。

性质1 事件发生后，辖区的应急医疗物资需求自然发展且不断加剧。在需求未被满足的情况下，需求状态是关于救援阶段的单调递增函数。

假设表示在t阶段时辖区j对应急医疗物资k的需求状态

其中：t1，t2∈T，1 ≤t1＜t2≤tmax。

性质2 事件发生后，辖区的应急医疗物资的需求状态随机变化，即是一个随机变量。

由于事件突发性导致需求变化的不确定，所以相邻阶段的需求状态随机转换。需求状态转移概率矩阵为：

其中：Pjk(θ1，θ2)为θ1状态转移到θ2状态的概率。由性质1 可知，Pjk是一个上三角矩阵。

定义1事件发生后，应急医疗物资的需求状态随事态发展而自然演变。设为第t阶段时，辖区j对于应急医疗物资k需求的原始状态。

在事件的不断演变中，只要某一阶段物资的需求状态确定，后序事件的随机演变仅与当前阶段的状态有关，而不受此前状态影响。即当前物资的需求状态是先序事件演变的完整总结。第t阶段的组成一条齐次Markov 链，且规定一个初始值为：

定理1设第t+1 阶段的原始状态下的应急医疗物资需求期望值。设Δt为两个相邻阶段之间的时间间隔，当Δt无限趋近于0 时，则：

定义2由于事件突发性，应急管理者很难做到连续决策。因此，设相邻阶段的原始状态转移方程为：

其中：round(x)函数对(x)随机取整，且尽量取到最相近的整数。

其中：rand为在[0，1]内的随机数，[x]表示对x取整。

定义3若某一阶段对应急医疗物资的需求可以满足，则需求状态的演变态势得到控制。设为第t阶段时，需求点j对于应急医疗物资k需求的“控制状态”。

假设在每一阶段都对各辖区作出决策：1）在该阶段配置物资；2）暂时不配置并推迟到下一阶段再决策。由于应急医疗物资的相对短缺，即使对某一辖区配置的物资也只能部分满足需求。设决策变量表示在第t阶段是否对辖区j配置应急医疗物资。

性质3 如果在第t阶段的需求得到控制，需求状态将重新回到初始值，之后需求状态重复从需求产生开始到加剧的Markov 过程。

事件发生后，应急医疗物资的需求在原始状态和控制状态之间转移，所以联立式（15）、（17）得出相邻阶段间的状态转移方程如下：

事件初期往往难以精确获得辖区实际需求量，通常以“2 000 件左右”“大概2 000 件到3 000 件”等不确定语言描述。为有效处理此类不确定信息，三角模糊数能够有效体现出需求的不确定性［29］。参照文献［30-31］的方法，采用三角模糊数理论来描述辖区的模糊需求。

对于三角模糊数的比较，可以运用该模糊数的整体期望值进行去模糊化处理。 证毕

性质4 城市辖区的需求与控制状态呈正比关系。则第t阶段辖区j对于应急医疗物资k的需求为：

最优配置策略就是以最小化所有阶段、所有辖区、所有应急医疗物资的需求总和为目标，则目标函数为：

其中：表示第t阶段应急医疗物资k的最大供应量。

4 模型求解

为应对突发公共卫生事件下的应急医疗物资配置问题，决策者必须在极短时间内作出决策，因此对模型求解算法有更高的要求。Karaboga等［32］提出ABC 算法，这是一种模仿采蜜行为的群体智能优化算法。相关学者的研究证明，相较于遗传算法（Genetic Algorithm，GA）、粒子群优化（Particle Swarm Optimization，PSO）算法等，ABC 算法具有较快的收敛速度、较少的控制参数、易于实现并有更好的优化性能［33-34］。

4.1 人工蜂群算法

在ABC 算法设计中，各角色主要分为：1）蜜源，指可以采集花蜜的位置，以花蜜浓度衡量价值；2）引领蜂，指已发现蜜源，对应特定蜜源位置的工作蜂；3）跟随蜂和侦察蜂，指未发现蜜源，正在寻找蜜源的待工蜂。ABC 算法中蜂群的采蜜动作与优化物资配置模型的对应关系如表2 所示。

表2 ABC算法与优化物资配置模型的对应关系Tab.2 Correspondence between ABC and optimal material allocation model

蜂群角色分工为：引领蜂寻找新的蜜源（物资配置策略）并与跟随蜂共享蜜源信息；跟随蜂依据共享信息，服从概率择取一个相对较好的蜜源采蜜；侦察蜂随机寻找新的蜜源（物资配置策略）。算法步骤如下。

1）初始化。首先随机生成N个蜜源，并与一个引领蜂相对应，设置引领蜂数量和跟随蜂相等。每个蜜源位置为，其中：i=1，2，…，N；M为问题的维度。对进行初始化：

2）引领蜂行为。引领蜂先在对应蜜源周围按照“贪婪原则”进行邻域搜索。若引领蜂搜索到蜜源的花蜜浓度大于原蜜源则替换蜜源，反之保留原蜜源，如式（26）所示：

其中：riM∈[ -1，1]为随机数，限制引领蜂的邻域搜索区域；p为[1，N]范围内的随机整数且p≠i，即与Xi不同的蜜源Xp；Mrand为[1，M]范围内的随机整数。

3）跟随蜂行为。在全体引领蜂结束搜索后，将与跟随蜂共享蜜源信息。跟随蜂将以轮盘赌方法择取蜜源，若蜜源浓度越高，则吸引来的跟随蜂越多。蜜源Xi被选中的概率为：

类似地，跟随蜂在新蜜源周围仿照式（26）的引领蜂行为进行搜索。如果新蜜源花蜜浓度大于原蜜源时，则选择新蜜源，并互相转换角色；反之，保持不变。

4）侦察蜂行为。如果某蜜源连续limit次没有被更替，说明这个蜜源处于局部最优，应当被舍弃。同时，引领蜂转换角色为侦察蜂，再按照式（24）产生新的蜜源。当搜索出新蜜源时，侦察蜂转换角色为引领蜂。

5）结束。保存在该时间节点的最优蜜源。如果满足循环结束条件，循环结束；反之，返回1）初始化直到满足循环结束条件后，循环结束。

4.2 二进制编码下的蜜源位置更新

本文提出的应急医疗物资动态配置模型，由于决策变量是0-1 变量，属于离散型求解问题，因此，需要对算法中的蜜源位置进行二进制编码处理。

二进制编码下，对蜜源位置进行更新，将实数解和ViM转换为二进制解具体转换方法为：

其中：rand'、rand″为在［0，1］内的随机数。

4.3 适应度函数设计

将约束（23）以惩罚函数的形式合并到式（22），得到独立的适应度函数：

所以求解模型中控制状态的问题，就转换为对元胞数组的元素进行选择的问题。

综上，求解提出模型的算法步骤如图2 所示。

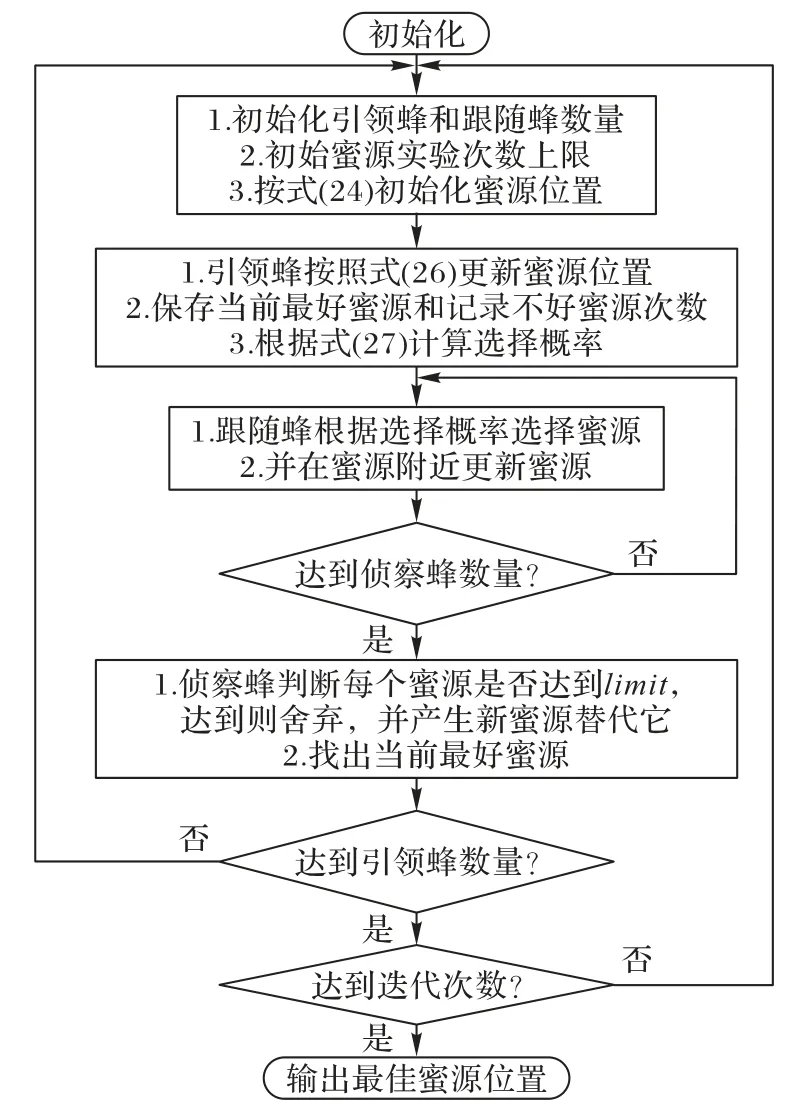
图2 算法步骤示意图Fig.2 Schematic diagram of algorithm steps

5 算例分析

5.1 辖区韧性评估

本文选择城市辖区作为基本单元，数据主要来源于2020年上海市各区统计局发布的统计年鉴和统计公报与各区卫健委、应急管理局等政府信息公开内容。将卫生系统韧性指标的原始数据分为正向和负向指标进行标准化处理，再转化为无量纲数据，采用熵值法确认权重。运用K-means 算法对各区的Rx、Rs和Rh进行聚类，聚类结果如图3 所示。

根据综合评分得出R1～R5分类标准，如表3 所示。R1～R5分别为低、中低、中、中高和高韧性，得到韧性分布图，如图4所示。分析可知，城市卫生系统韧性中恢复和适应能力是主要影响因素，较大程度地影响着卫生系统韧性。由于人口密度等客观条件约束，虽然部分高韧性辖区的吸收能力低于低韧性辖区，但是较强的恢复和适应能力使它保持高韧性。从区域分布来看，上海市的中心城区普遍处于中韧性以上，辖区之间韧性差异较大，郊区普遍处于中低韧性，辖区之间的韧性差异不大。因此，本文选择中心城区（A～F）展开研究。

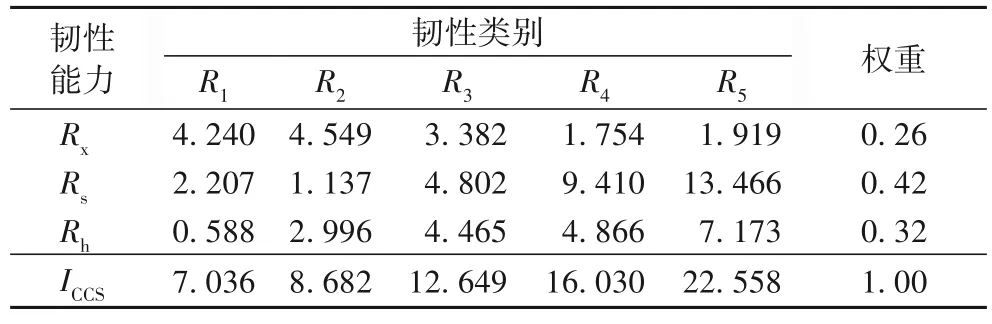
表3 韧性分类标准 单位：%Tab.3 Resilience classification standards unit：%

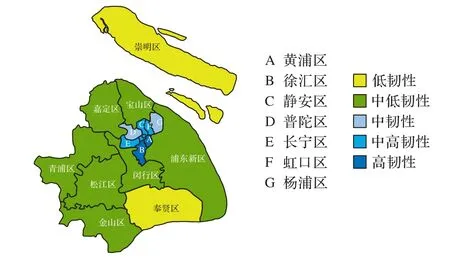
图4 上海市卫生系统韧性分布Fig.4 Distribution of Shanghai health system resilience

5.2 应急医疗物资配置

5.2.1 算例描述

算例将选取中心城区的应急医疗物资配置问题进行研究。公共卫生事件发生后，辖区的应急医疗物资（如口罩、防护服等）常规储备迅速消耗，应急医疗物资储备不可能同时满足全部辖区需求。假设配置阶段共有4 个阶段T={t|1，2，3，4}，在某一阶段内各个辖区对于应急医疗物资共有4 种需求状态，表示不同物资需求程度。各辖区的基准需求和状态初值如表4 所示。

表4 各辖区信息统计Tab.4 Information statistics of each area

各个需求状态转移概率矩阵如表5 所示。假设每个阶段应急医疗物资储备库的供应分别为口罩15 000 件、防护服3 000 件。由于辖区之间存在着卫生系统韧性的差异，先满足哪些辖区后满足哪些辖区是亟需研究的问题。

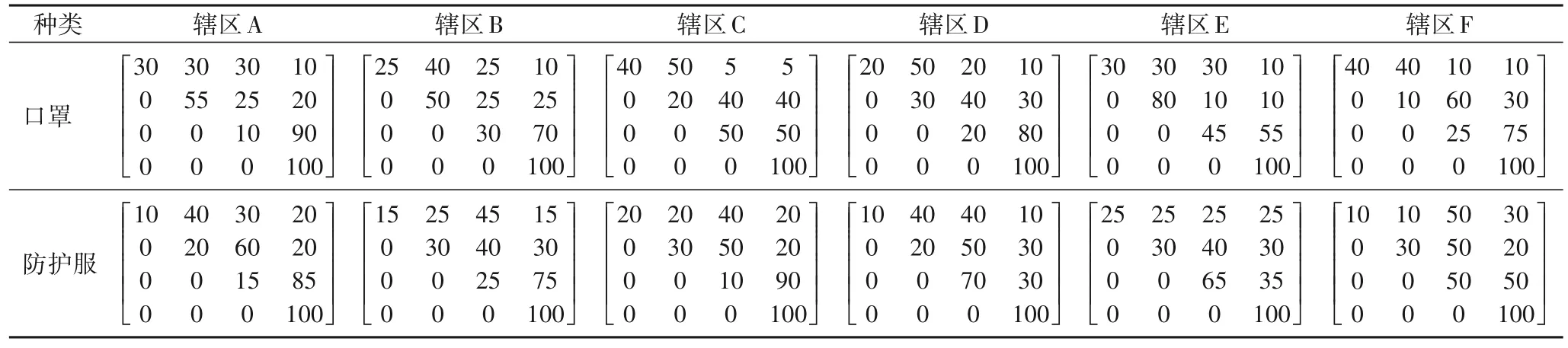
表5 各辖区对应急医疗物资的需求状态转移概率矩阵 单位：%Tab.5 Probability matrix of demand state transfer for emergency supplies in each area unit：%

5.2.2 算例求解

本文实验的软硬件环境如下：CPU 为Intel Core i7 2.8 GHz；内存为16 GB；操作系统为64 位Windows 10，通过Matlab R2016a 编程求解。ABC 算法的参数设置如下：种群大小为200，最大迭代次数为200，limit为分别为10、-10，充分大的正数Q设置为108。连续运行程序10 次，适应度值的范围是［9.138 9，10.455 6］，求解时间的范围是［7.2，8.5］，求解的适应度值的变化曲线如图5 所示。可以看出，算法在初期快速收敛，可以快速迭代寻优，求解结果具有较强稳定性。因此，可以满足应对突发公共卫生事件时快速高效决策的要求。

图5 适应度函数的变化曲线Fig.5 Change curve of fitness function

5.2.3 结果分析

根据需求状态的演变绘制原始状态与控制状态的变化曲线，如图6 所示。其中：口罩需求状态用MS表示；防护服需求状态用FS表示。将式（22）中不同辖区的韧性Rj设为相同值，以对比是否考虑辖区韧性差异对物资配置策略的影响。

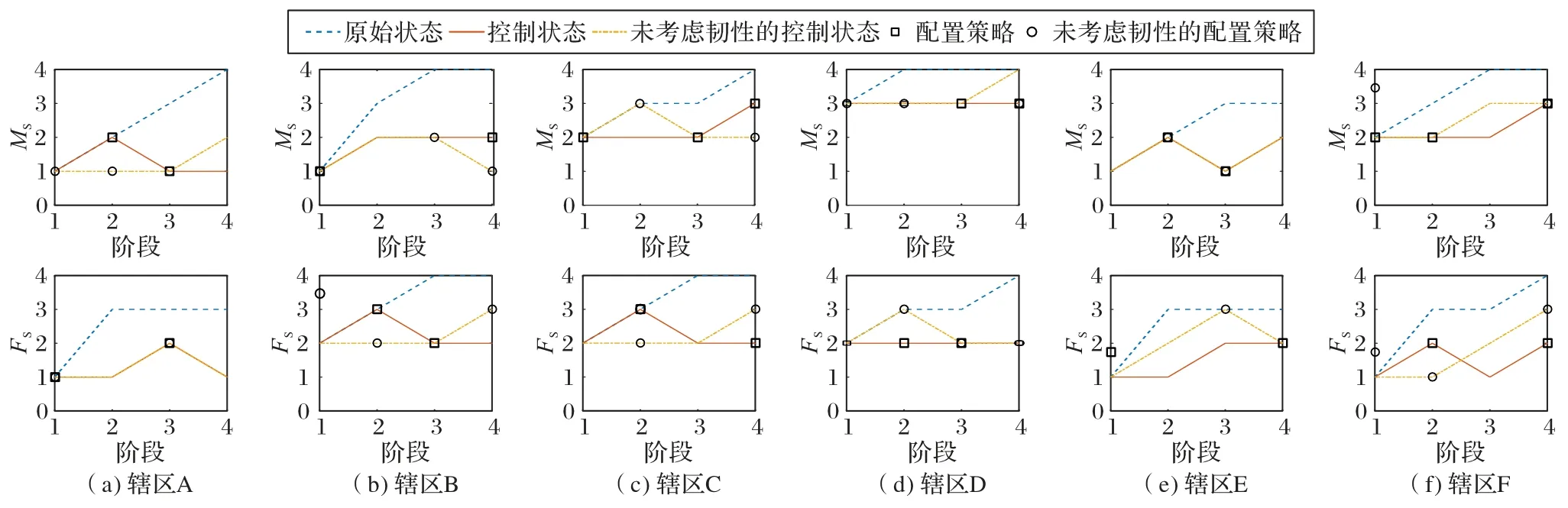
图6 原始状态与控制状态的变化曲线Fig.6 Change curves of original state and control state

突发事件下应急医疗物资供需关系极不平衡，由于物资供应的相对不足，所以需要选择性地满足各辖区的部分需求，以避免需求状态的持续加剧。各阶段的最优策略如表6所示，其中：K 表示口罩；F 表示防护服。

由表6 可以发现：事件发生后，原始状态下各辖区应急医疗物资需求将迅速增长，甚至部分辖区达到了极值。这意味着若不采取措施，辖区的公共卫生安全将面临挑战，不利于保障辖区居民的物资供应及生命健康。

表6 应急医疗物资最优配置策略Tab.6 Optimal allocation strategy of emergency medical supplies

对于需求的随机演变，模型可以动态地控制辖区的物资需求，并且有效的物资配置策略可以使需求状态变化趋于平稳。在供需关系极不平衡的情况下，能够更快地对韧性水平相对较低、需求状态变化大、物资需求量大的辖区进行配置。物资配置总量如图7 所示，本模型的配置总量整体少于初始配置量，配置策略能在经济性前提下有效控制需求，充分满足了突发公共卫生事件所要求的效率性、科学性。

考虑韧性的配置策略对于韧性相对较弱的辖区（如D、E、F）配置次数多于其他辖区，需求状态曲线波动次数明显减少，需求状态被较好地控制。从图7 也能看出，相较于传统的平均分配，模型提出的配置策略能够动态调整物资配置量，在配置时向卫生系统韧性薄弱的辖区倾斜。这也体现了在应急医疗物资配置中要求的公平性。

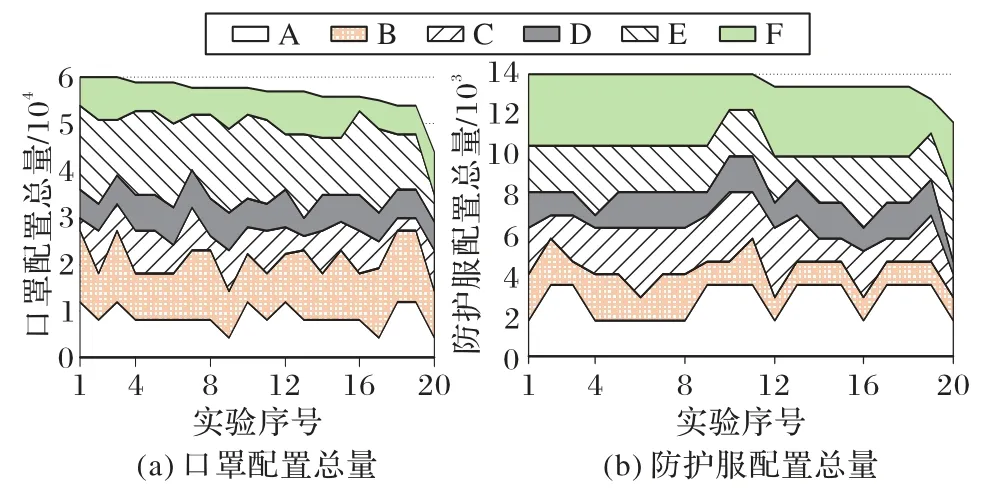
图7 物资配置总量统计Fig.7 Statistics of total number of material allocation

综上所述，本文模型可以客观描述在公共卫生事件发生后，事件演变的随机性和多阶段性。在应急医疗物资配置策略中，考虑了应急决策要求的时效性、公平性和科学性，对于城市的应急医疗物资配置有一定的指导意义。

6 结语

本文主要研究了突发公共卫生事件下，基于韧性视角的城市内应急医疗物资动态配置的问题。在模型建立上：1）对城市辖区间的卫生系统韧性进行了评估分级，有助于在决策时直观考虑辖区韧性。2）根据事态不断演变的突发公共卫生事件，应急医疗物资的供需关系极不平衡的特性，采用齐次Markov 过程建模。采用二进制ABC 算法求解，得出最优的应急医疗物资配置策略。研究表明：1）在物资配置研究中，采用Markov 链可以动态描述需求的变化，为制定动态配置策略起到了积极作用；2）考虑辖区卫生系统韧性，有助于在动态配置中向韧性较弱的辖区倾斜。此外，在复杂应急物资配置方式、城市内运输方式限制、事件信息非完全可观测情况下如何进行物资配置有待进一步研究。