基于节点综合重要度排序的服务功能链部署优化方法

胡海岩，康巧燕*，赵朔，王建峰，付有斌

（1.空军工程大学 信息与导航学院，西安 710077；2.中国人民解放军93107部队，沈阳 110141）

0 引言

网络功能虚拟化（Network Function Virtualization，NFV）技术是云服务提供商为了降低投资与运营成本，将服务功能与底层硬件进行解耦的产物。NFV 可以在传统的专用硬件设备上实现虚拟网络功能（Virtualized Network Function，VNF）［1］，将这些VNF 根据请求按照一定的逻辑顺序连接形成服务功能链（Service Function Chain，SFC）。

随着5G 网络时代的到来，网络通信系统需要更低的时延，在有些特殊场景下甚至到达了毫秒级［2］，且在非理想环境下，基于软件的网络功能更容易出现硬件或软件故障，从而导致网络服务的中断，造成不可估量的损失。因此在部署SFC 的过程中，提高部署可靠性、降低端到端的时延成为了研究热点。本文在该热点问题的基础上，同时考虑降低节点、带宽资源的开销以达到降低运营商部署成本的目的。

针对可靠性问题，部分学者通过故障发生后的恢复机制进行研究，如文献［3］中用蒙特卡洛树搜索算法实现物理链路发生故障后的重映射问题；但这种恢复机制会暂停服务，影响服务质量。因此大部分学者通过备份增加冗余的方式进行研究：文献［4］中对整条链路进行备份；文献［5］中采用共享备份的方式以降低资源消耗；文献［6］中对VNF 进行联合备份，在提高可靠性的同时优化网络资源分配；文献［7］中提出一种相邻VNF 备份、实例资源共享的备份机制，在降低节点和带宽资源开销的同时提高了网络服务的映射成功率。但上述通过备份提高部署可靠性的方法会扩展SFC 的长度，不但会增加资源开销，而且也会在一定程度上增加时延，导致运营商部署成本增加，传输效率降低。因此，本文通过聚合VNF 来减少部署的网络节点，从而提高链路可靠性。

针对VNF 部署的问题，许多研究采用基于迭代的启发式算法，如文献［8］中将SFC 构建与映射同时混合编码，并采用改进的遗传粒子群算法对问题进行求解；文献［9］中提出将遗传算法与模拟退火算法相结合的求解策略，通过判断个体约束性与纠正遗传的方法避免局部最优的出现，大幅降低了端到端时延。但这种启发式算法需要反复迭代，消耗时间较多，不利于VNF 的快速部署，难以应用于某些低时延的场景。文献［10］中使用深度强化学习进行SFC 的部署，在保证可靠性的同时最大化映射成功率。文献［11-12］使用机器学习来部署VNF，这类方法能够明显提高SFC 的优化效果，但又依赖于利用大量准确的数据集训练模型。因此，本文依据可靠性、时延与拓扑属性定义了节点综合重要度以实现底层网络节点的排序，优化VNF 的部署。

针对VNF 聚合［13］问题，文献［14］中通过聚合功能相同的VNF 以达到降低映射成本的目的，但仅局限于相同功能的VNF 聚合，且未考虑到聚合后资源需求的增多会降低映射时的映射成功率。文献［15］在聚合相同VNF 的基础上，发现贪婪算法能够有效降低总带宽的消耗。文献［16］中通过共享节点来节省节点资源，并通过迁移调整提高资源利用率，此外还详细描述了带宽消耗与节点资源消耗之间存在的矛盾，但并未直接解决这种矛盾。文献［13］中为了解决这种矛盾，首先通过聚合不同的VNF 来降低节点资源消耗；然后通过一种能进行映射反馈的闭环算法有效地在降低节点资源消耗的同时降低带宽消耗；并且引入了节点亲密度的概念，通过降低节点跳数来降低需求带宽。文献［17］中介绍了6 种反映不同拓扑属性的互补特征，并根据这6 种特征的不同特点提出了三种基于拓扑感知的虚拟网络映射算法。文献［18］中针对节点资源与带宽的冲突设计了三种有效的策略，分别是重用虚拟机（即聚合相同VNF）、组合相邻不同的VNF 与临时链路映射，然后通过性别战博弈（Battle of Sexes，BoS）模型解决这类冲突问题，但并未给出具体的聚合方式。文献［19］中通过功能性约束、资源约束对节点进行聚合，有效地提高了可靠性，但并未考虑到不同VNF 对链路流量的影响不同。文献［20］中根据虚拟链路流量变化对VNF 进行聚合，从而提高可靠性。本文通过改进基于流量改变率的VNF 聚合方法以减少部署的网络节点，提高可靠性。

针对上述问题，本文以提高链路可靠性、降低节点资源与带宽消耗为目标，首先针对不同带宽需求的VNF，引入了流量改变率的概念［21］，通过流量改变率聚合VNF，聚合方式是将相邻的、流量改变率同小于等于1 或大于等于1 的不同VNF 进行聚合，从而减少部署的物理节点，提高链路可靠性，节约节点资源消耗与链路带宽开销，同时随着链路跳数的减少，端到端的时延也会随之降低；其次通过节点的度、可靠性、综合时延与链路跳数定义了节点综合重要度，对节点进行评价、排序，提高VNF 的映射效率；然后将聚合后的VNF依次映射到完成排序的底层节点上，映射过程要求映射的第i个节点到目标点的跳数不能大于第i-1 个节点到目标点的跳数，以此减少流量“乒乓效应”（在两节点之间往返传输）的出现，从而降低带宽开销；最后用k-最短路径算法映射虚拟链路，完成整个SFC 的部署。

1 模型建立与问题描述

1.1 网络模型

物理网络表示为一个加权无向图GS=(N，L)，其中：N为物理节点的集合，每个物理节点能够承载多个服务器，用来实例化VNF；L为物理链路集合。对于任意节点n∈N，Cn表示剩余可用计算资源，Mn表示剩余可用存储资源，Fn表示剩余可用转发资源，Ha，b表示物理节点a与节点b之间的跳数，rn为物理节点的可靠性，dn为实例化VNF 后产生的时延（节点时延）。对于任意物理链路La，b∈L，用Ba，b表示剩余带宽资源，Da，b表示链路时延。

SFC 请求为有向图Gv=(Ig，Og，Dg，Tg，Rg，Vg，Lg)，将SFC的集合表示为S={Sg|g=1，2，…}，Ig与Og分别表示第g条SFC 的源点与目标点。对于任意一条Sg，Ig与Og的物理节点确定后，Dg为SFC 的最大时延限制，Tg为SFC 的生存时间，Rg为SFC 的可靠性要求下限，Vg={fi|i=1，2，…} 表示Sg所有的VNF 集合，对于任意一个fi∈Vg，Cg，i、Fg，i和Mg，i分别表示它的计算资源需求、转发资源需求与存储资源需求。用ηg表示流量改变率，Sg的路由集合表示为Lg=(l0，1，l1，2，…，li-1，i)，用li-1，i表示第i-1 到第i个节点的路由，其中：0 为源点，i为目标点。bi-1，i表示第i-1 到第i个节点的带宽需求，可用式（1）表示，即经过任意VNF 后，带宽需求为流入的流量与VNF 流量改变率的乘积，Ball为链路总带宽消耗。

如果Sg中第k个VNF 成功部署在底层网络第i个节点上，则设μk，i=1；若不是则μk，i=0。若虚拟链路li-1，i成功映射到物理链路La，b上，则否则的可靠性可用式（3）表示，其中Rg为链路可靠性，即各部署成功的网络节点可靠性之积。

设节点资源开销为costall，可用式（4）表示，即节点的计算、存储与转发能力之和。

1.2 优化目标

本文的主要目标是在提高链路可靠性的同时降低带宽开销与节点资源开销，由此设定目标函数为：

式（8）保证SFC 中的一个虚拟功能只能映射到一个底层节点，防止VNF 分割；式（9）保证虚拟链路能够映射在一条或多条物理链路上；式（10）表示一条物理链路上只允许布置至多一次虚拟链路；式（11）～（13）分别为计算、存储与转发能力约束，不等式左边为每个节点的资源消耗，为了实现负载均衡［19］，保证每个节点的资源消耗不超过它的总资源的90%；式（14）表示链路带宽约束，式（15）表示时延约束，不等式左边为节点时延与链路时延之和。

1.3 问题描述

SFC 的部署问题分为SFC 的构建与映射两个部分。

SFC 的构建过程需要考虑VNF 的依赖关系，若VNF2 依赖于VNF1，则流量必须先经过VNF1 的处理后才能到VNF2。如入侵检测系统要在网络保密器之前执行，解码器在编码器之后执行，本文假设VNF 顺序已知，不考虑构建问题。SFC 的映射过程需要考虑两个问题：

1）网络节点的资源限制。一个节点可部署的VNF 有限，如5G 边缘数据中心处理数据的能力十分有限。

2）VNF 映射节点的位置。VNF 会改变流量速率，例如防火墙会丢掉某些数据包导致输出速率小于输入速率，而虚拟专用网络（Virtual Private Network，VPN）代理会给数据报文新增头部开销从而导致输出速率大于输入速率。

图1～4 展示了同一条SFC 在相同的网络结构中的不同部署方法，其中：VNF 上的数字代表流量改变率［22］；B为链路总带宽，箭头与序号代表数据流经过的顺序。

不同的VNF 部署位置会产生不同的带宽消耗，图1（a）为将流量改变率小的VNF 靠后部署的方法；图1（b）为将流量改变率大的VNF 靠后部署的方法。通过对比可以看出图1（a）方法的所需带宽高于图1（b）方法，所以相同路径的不同VNF 部署位置所需带宽不同。

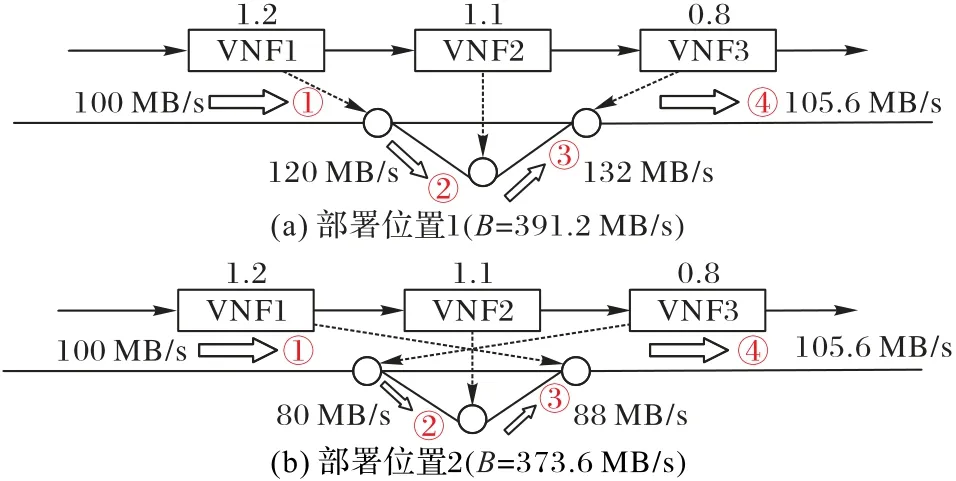
图1 不同部署位置的VNF部署方法Fig.1 VNF deployment methods with different deployment locations

不同路径的带宽消耗也不同，如图2 所示，对VNF 进行聚合，聚合后的VNF 节点资源需求为各VNF 节点资源需求之和，流量改变率为各VNF 节点改变率之积，可以看出图2（b）方法的带宽消耗小于图2（a），所以链路跳数越小带宽消耗越少。

图2（c）展示了两节点之间的“乒乓效应”。图中两节点中的一条链路经过了往返两次传输，与图1（b）相比，VNF 部署位置相同，但流量所经路径不同，可以看出图2（c）方法所需带宽远高于图1（b），因此在链路传输中应尽量减少“乒乓效应”以提高传输效率，降低带宽消耗。

图2 不同路径的VNF部署方法Fig.2 VNF deployment methods with different paths

不同的VNF 聚合方式的带宽消耗也不同，如图3 所示。图3（a）与图3（b）的部署方式相同，但是两者采用了不同的聚合方式，可以看出图3（b）方法的带宽消耗大于图3（a）。

图2（a）、图2（b）、图3（b）方法都采用了聚合的方式将3个VNF 部署到两个节点上，假设每个节点的可靠度为0.95，则这种聚合后的链路可靠度为0.952=0.902 5。图1（a）、图1（b）、图2（c）方法将3 个VNF 分别部署到3 个节点上，链路可靠度为0.953=0.857 4。因此同样数量的VNF 下，对VNF 进行聚合处理能够减少映射的网络节点数量，从而提高链路的可靠性。

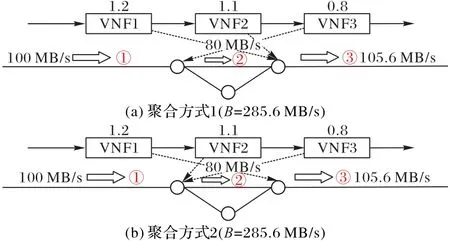
图3 不同聚合方式的VNF部署方法Fig.3 VNF deployment methods with different aggregation methods

经过比较可得，图2（b）方法在6 种部署方法中带宽消耗最小。因此在理想状态下，以最优的聚合规则对VNF 进行聚合，再将带宽需求较小的VNF 靠前部署、带宽需求较大的VNF 靠后部署，并且选择链路跳数最小的节点依次部署，同时减少链路的“乒乓效应”，就能以最优的方式降低链路带宽消耗并提高链路可靠性。但在非理想状态下，由于部分VNF具有依赖关系，映射到底层网络也应保持这种依赖关系，因此本文不考虑VNF 的靠前部署与靠后部署，而是依次对VNF 进行部署。

图4 为非理想状态下的VNF 部署方法，带宽消耗相较于图1、图2（a）、图2（c）方法仍具有优势。同时，将图4 方法与图1（a）相比较可以看出，通过VNF 聚合也可达到将流量改变率小于1 的VNF 靠前部署的目的，从而降低链路的带宽消耗。

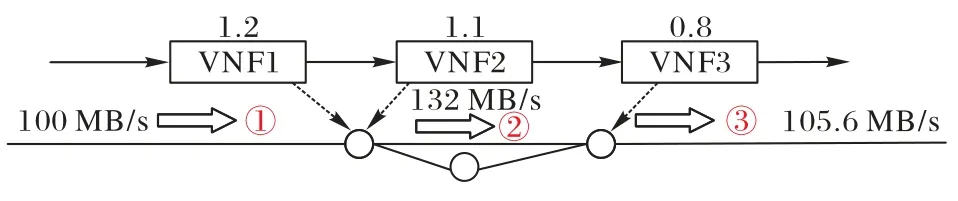
图4 最终VNF部署方法（B=337.6 MB/s）Fig.4 Final VNF deployment method（B=337.6 MB/s）

2 流量与可靠性优化的VNF部署设计

本章首先采用基于流量改变率的VNF 聚合方法对VNF进行处理，然后对底层节点按照节点综合重要度进行评价与排序，将聚合后的VNF 依次映射到完成排序的底层节点上，最后采用k-最短路径算法映射虚拟链路。

2.1 基于流量改变率的VNF聚合方法

本节涉及两个概念：聚合与流量改变率。

文献［13］中指出当一个多功能物理设备能够提供多种网络功能与足够的计算能力时，可以将来自同一SFC 请求的多个VNF 映射到同一物理设备上，即聚合原SFC 序列中资源需求与功能不同的VNF，以提高物理资源利用率与链路的可靠性。本文通过流量改变率聚合VNF，而流量改变率η［21］即流量通过VNF 后，流出的流速率与流入的流速率之比，可将它分为三类：1）η＜1 的VNF，即流出流量小于流入流量，如防火墙、网络加速器、解码器等；2）η=1 的VNF，即流出流量等于流入流量，如入侵检测、负载均衡器等；3）η＞1 的VNF，即流出流量大于流入流量，如编码器、网络保密器、VPN 代理等。

本文聚合VNF 的主要思路为：在一个序列已知的SFC中，分别聚合η≤1、η≥1 的相邻VNF，由于“1”不改变聚合后的VNF 流量改变率，因此既可与η＜1 的相邻VNF 聚合，也可与η＞1 的相邻VNF 聚合，这样能够最小化聚合后的VNF 数量。本文将η=1 的VNF 与前一个VNF 做相同处理，即当前一个VNF的η＜1 时，η=1 的VNF 当作小于1 处理；当前一个VNF的η＞1 时，当作大于1 处理。聚合后的VNF将映射到同一物理节点上，其中聚合后的VNF 节点资源需求为各VNF 节点资源需求之和，流量改变率为各VNF 节点改变率之积。

如图5 所示，VNF 下的数字为流量改变率η，聚合方法1中VNF1 与VNF2的η＜1，可以进行聚合；VNF3 与VNF4的η＞1，可以进行聚合，聚合完成后，部署VNF 的节点由原始的4 个变为2 个，不仅可以提高链路的可靠性，同时也可达到将η＜1 的VNF 靠前部署的目的，以降低链路带宽消耗。在聚合方法2 与聚合方法3 中，η=1 的VNF3 既可与η＜1 的相邻VNF 聚合，也可与η＞1 的相邻VNF 聚合。在聚合方法4 与聚合方法5 中，当η=1 的VNF3 既与η＜1 的VNF 相邻，又与η＞1 的VNF 相邻时，则规定VNF3 与前一个相邻的VNF 聚合。聚合方法6 为特殊情况，由于相邻的VNF 之间没有同小于等于1 或同大于等于1 的VNF，所以无法进行聚合。设本文的聚合方式为J1。

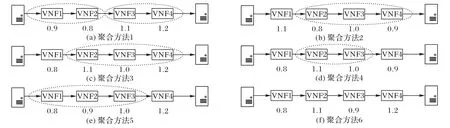
图5 不同流量改变率的VNF聚合方法Fig.5 VNF aggregation method based on different traffic change rate

文献［20］中同样采取基于带宽需求变化的VNF 聚合方式进行处理，它的聚合方法为将η＞1 的VNF 与之后的所有η≤1 的VNF 进行聚合，直到下一个η＞1 的VNF 为止。设文献［20］的聚合方式为J2。为了与文献［20］具有相同的VNF 聚合条件，设置一种新的聚合方式J3：在一个序列已知的SFC 中，分别聚合η≤1、η＞1 的VNF。

如图6 所示，将SFC 中VNF 数量为4 的情况通过树状图的方式 全部列 出，其中：A为η＞1 的VNF；B为η≤1 的VNF。数字为以不同方式聚合后的VNF 数量，J3为40，J2为47，可看出按照J3聚合的VNF 数量小于按照J2聚合的VNF数量，因此相较于J2，J3的聚合效果更好。

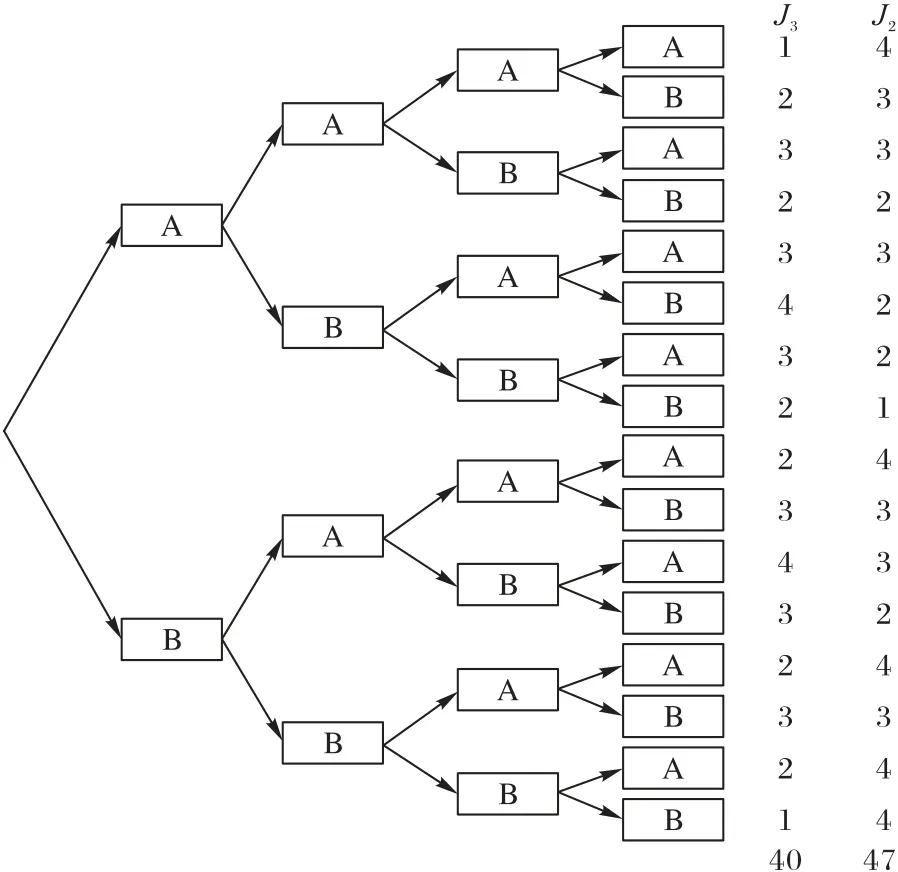
图6 J2与J3的对比结果Fig.6 Comparison result of J2 and J3

而本文的聚合方法J1与J3相比，聚合判定条件由η=1的VNF 只能与小于1 的VNF 聚合，更改为η=1 的VNF 既能与小于1 的VNF 聚合也能与大于1 的VNF 聚合，聚合效果更好。如图7 所示，在相同情况下，按照J1方法聚合可将VNF数量从4 个聚合成2 个，而按照J3方法聚合仍然是4 个VNF，因此可得出J1的聚合效果优于J3。

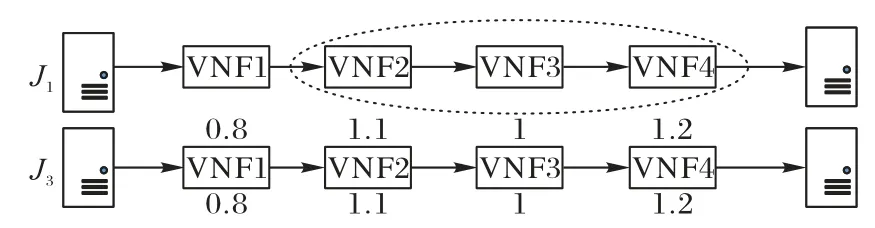
图7 J1与J3的对比结果Fig.7 Comparison result of J1 and J3

因为J3的聚合效果优于J2，可以说明：在相同情况下，J1的聚合效果优于J2。因此在VNF 数量较小的情况下（本文为3～6 个），本文的聚合效果更好，能够节省更多的带宽资源，提高链路可靠性，降低时延。基于流量改变率的VNF 聚合的具体步骤如算法1 所示：

算法1 基于流量改变率的VNF 聚合方法。

输入 VNF 集合V，集合中每个VNF 的对应流量改变率η；

输出 完成聚合的VNF 集合V′。

聚合后的VNF 节点资源需求为各VNF 节点资源需求之和，流量改变率为各VNF 节点改变率之积。

2.2 基于节点综合重要度的节点排序与SFC映射

VNF 聚合完成后，需要将它们映射到底层物理节点上。受文献［20，22］工作的启发，本文综合考虑物理网络节点之间的关系与时延感知，通过分析节点的度、链路跳数、可靠性、综合时延四者与节点综合重要度的相关性对节点进行评价与降序排序，然后将2.1 节完成聚合的VNF 依次映射至完成排序的节点上，最后通过k-最短路径算法映射虚拟链路，完成整个SFC 的部署。

根据节点综合重要度对网络节点进行排序，可分为两个部分：1）对底层网络拓扑进行感知，主要考虑节点的度与链路跳数；2）在此基础上综合考虑节点综合时延与可靠性。具体如下：

①根据节点的拓扑结构考虑节点的重要度。首先衡量一个节点n的重要度的关键是节点的度，即节点与邻近节点之间直接链接的链路数目。相同情况下，节点的度越大，节点重要度越大，二者呈正相关。节点的度NDn为节点n与邻近节点之间相连的链路数量之和，可表示为：

由图2 的分析可知，链路跳数越小，它的映射节点距离越近、范围越小，带宽消耗就越小，越有利于节点的排序，因此链路跳数与节点重要度呈负相关。本文用节点n与源点Ig的跳数hn，Ig、节点n与目标点Og的跳数hn，Og之和表示链路跳数，链路跳数Hn可表示为：

综上所述，节点的度与节点重要度呈正相关，链路跳数与节点重要度呈负相关，因此可将节点的重要度Xn表示为：

②除了考虑节点重要度外，还综合考虑了节点的可靠性与综合时延。节点的可靠性rn即节点的故障间隔Fn占故障间隔Fn与修复时间Rn之和的比值［23］，可表示为：

节点可靠性越高，越有利于节点的排序，因此节点可靠性与节点的重要度呈正相关。

网络时延即一个报文或分组从网络一端到另一端所消耗的时间，通常由节点的处理时延、排队时延、传输时延与链路的传播时延组成，本文用节点的综合时延表示。节点的综合时延ZDn为节点时延dn与相邻链路综合时延之和，其中相邻链路的综合时延为节点相邻链路时延Dn之和与节点的度NDn的比值：

节点综合时延越小，越有利于节点的排序，因此节点综合时延与节点的重要度呈负相关。

综合考虑上述各指标与节点重要度的关系，可将节点综合重要度Yn表示为：

由此可通过多指标计算出各个节点的综合重要度，并按照综合重要度对各节点进行评价与排序，能够显著提高映射效率。具体流程如算法2 所示。

算法2 基于节点综合重要度的节点排序。

输入 物理网络GS=(N，Ln)；

输出 完成排序的节点集合N′。

在VNF 聚合映射策略中，为了减少链路的“乒乓效应”，降低带宽消耗，要求映射的第i个节点到目标点的跳数不能大于第i-1 个节点到目标点的跳数（如图2（c）所示的“乒乓效应”，映射的第3 个节点到目标点的跳数大于映射的第2 个节点到目标点的跳数），对于不符合要求的节点直接删除；然后依次将完成聚合的VNF 映射到完成排序的节点上，完成VNF 的部署；最后通过计算链路的可靠性判断是否达到标准要求，若不达标则VNF 部署失败。具体流程如算法3 所示。

算法3 基于节点综合重要度的节点排序。

输入 聚合VNF 后的SFC 序列(I，O，D，T，R，V′，L′)，排序后的物理链路Gs=(N′，Ln′) ；

输出 VNF 映射List。

最后在满足约束式（9）、（14）～（15）的条件下，采用k-最短路径算法，将两个虚拟节点间的虚拟链路映射到相对应的底层物理链路上，完成整个SFC 的部署。

3 性能评估实验与结果分析

为了验证方法的有效性，采用Matlab 仿真软件对本文方法进行评估分析，通过特定的评价指标，与基于服务质量（Quality of Service，QoS）保障的服务功能链动态部署方法［2］、基于流量优化的可靠服务功能链部署方法［20］、可靠性感知的资源节约型虚拟网络功能部署方法［24］作对比。同时本文为了与文献［20］中提出的聚合方式进行比较，为验证图6 的树状图结果，设置了一个对照实验，该实验采用文献［20］中的聚合方式，其余设置与本文一致。

3.1 评价指标

本文通过SFC 平均可靠性、平均端到端时延、平均带宽开销、长期平均开销比、映射成功率评价方法的性能。

1）Sg的可靠性Rg由式（3）可得，则它的平均可靠性为：

其中：Nsuc为成功部署SFC 的数量。

2）Sg的端到端时延Dg为：

则它的平均端到端时延可定义为：

3）Sg的平均带宽开销Bcostave可定义为：

其中：Bcostg为部署成功后Sg消耗的带宽。

4）Sg的映射成功率ωacc可定义为：

其中：Nsuc(T)表示在时间T内SFC 部署成功的数量；Nv(T)表示在时间T内SFC 请求到达的数量；δ为无穷小，防止Nv(T)为0。

5）在t时刻，将成功部署一个Sg的收益定义为：

在t时刻，成功部署一个Sg，底层物理网络的开销为：

其中：α、β、χ和γ分别表示收益与开销中节点计算资源、存储资源、转发资源以及链路带宽资源各自所占的比重，本文均设定为1。

Sg的长期平均收益开销比为：

3.2 仿真环境设置

本文基于Matlab R2016b 仿真软件对方法进行评估。物理网络为100 个节点与525 条链路组成的连通图，是一个中型网络拓扑图。具体参数设置如表1 所示。

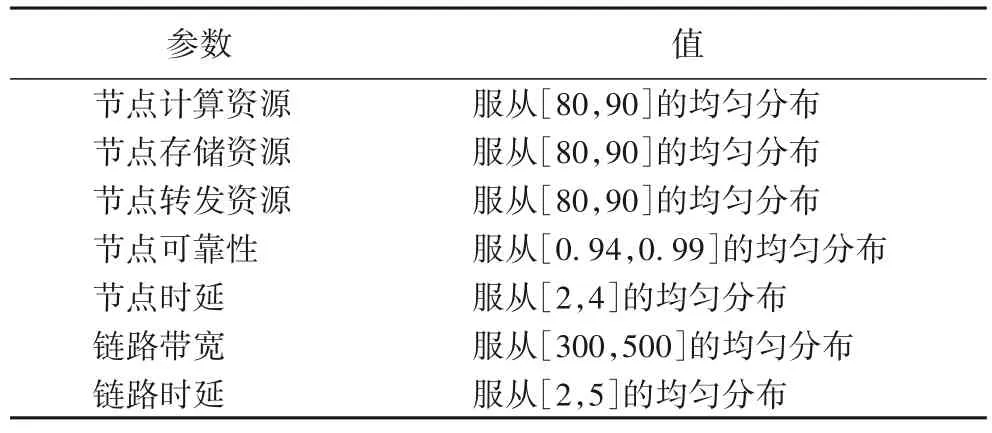
表1 物理网络参数设置Tab.1 Physical network parameter setting

SFC 设置：SFC 请求到达率服从λ=1/20 的泊松分布，生存周期服从μ=1 000 的指数分布，仿真实验持续6× 104个时间单位。具体参数设置如表2 所示。

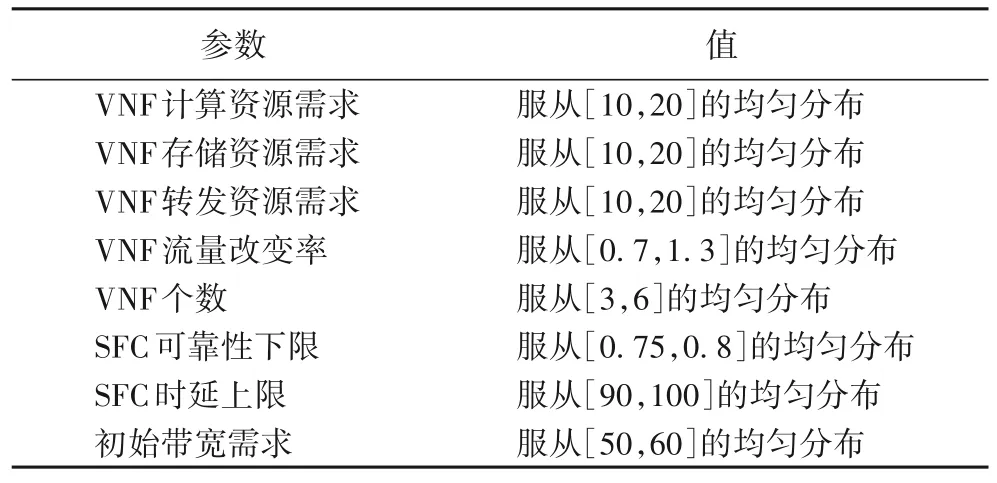
表2 SFC参数设置Tab.2 SFC parameter setting

为降低随机因素的影响，仿真实验共进行了10 次，并选取每次结果的平均值作为实验的最终结果。

3.3 实验结果分析

在相同的物理网络环境与SFC 请求下将本文方法与文献［2，20，24］中的方法和本文对照实验方法进行对比实验仿真，5 种方法的具体对比如表3 所示，所有方法均采用k-最短路径映射虚拟链路。其中：本文的VNF 聚合方法用J1表示，文献［20］中的聚合方法用J2表示。

表3 不同VNF部署方法对比Tab.3 Comparison of different VNF deployment methods

分别从SFC 平均可靠性、重复映射链路跳数、平均端到端时延、平均带宽开销、长期平均收益开销比与映射成功率6 个方面进行分析。

从图8 可以看出，本文方法、文献［20］方法与对照实验方法的映射成功率远高于文献［2］与文献［24］方法，达到了0.95 以上。因为在部署的过程中，这3 种方法不仅考虑了节点的拓扑位置，还考虑了节点的可靠性与综合时延，约束条件更加完善，大幅提高了映射成功率。文献［2］方法没有考虑链路时延，文献［24］方法不仅没有考虑链路时延，也没考虑节点时延，只关注链路的可靠性，使SFC 部署成功后的时延约束不足，导致映射成功率较低。

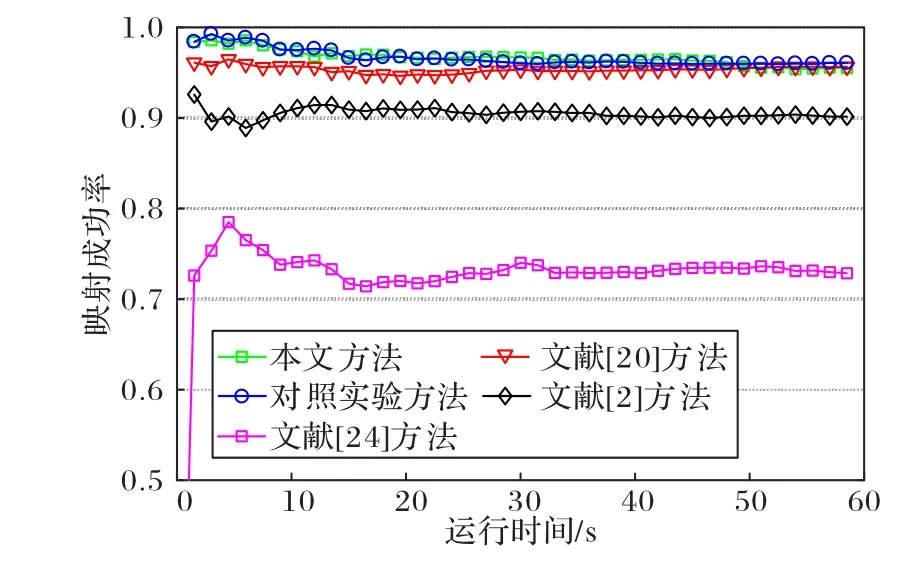
图8 SFC映射成功率Fig.8 SFC mapping success rate

如图9 所示，相较于文献［20］方法，本文方法的长期平均收益开销比θ提高约16%。本文方法、文献［20］方法与对照实验方法的θ远高于文献［2］与文献［24］方法，本文方法的θ更是达到了0.95 以上，明显优于其他方法。由于本文方法、文献［20］方法与对照实验方法首先考虑了VNF 的聚合，大幅降低了节点的资源消耗与带宽消耗，其次考虑了“乒乓效应”，有效降低了带宽的开销，显著提高了θ。对照实验方法与文献［20］方法相比，节点排序方式不同，收益开销比却大幅提升，说明用节点综合重要度对节点进行评价与排序更加有效，能够让不同的评价指标对节点的排序起到更加有效的作用，从而降低了节点资源与带宽的开销，提高了θ。本文方法与对照实验方法相比，VNF 聚合方式不同，收益开销比结果也有所提高，说明本文的聚合方式更加有效，能够减少更多的部署节点，从而降低节点资源消耗与链路带宽消耗，提高θ。

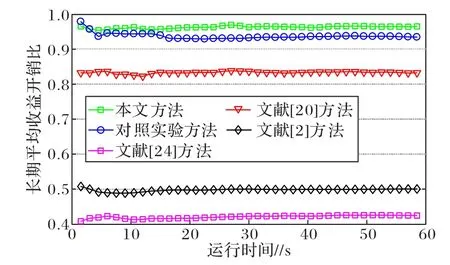
图9 长期平均收益开销比Fig.9 Average long-term revenue-to-cost ratio

由图10 可以看出，本文方法、文献［20］方法、对照实验方法与文献［2］、文献［24］方法相比，平均重复映射链路条数更少。因为这3 种方法都考虑了“乒乓效应”，而文献［2］、文献［24］方法未考虑这种特殊情况，“乒乓效应”会显著增加链路重复映射条数，从而增加链路带宽消耗。本文方法、文献［20］方法与对照实验方法在VNF 映射时考虑了链路跳数的约束，从而降低了链路重复映射条数。

图10 链路重复映射条数Fig.10 Link number of duplicated mapping

由图11 可以看出，本文方法、文献［20］方法、对照实验方法、文献［24］方法与文献［2］方法相比，SFC 的平均可靠性Rg都在0.9 以上，本文方法的Rg更是达到了0.92 以上，相较于文献［20］方法提升了约2%。因为本文方法、文献［20］方法、对照实验方法都对VNF 进行聚合处理，大幅降低了底层物理节点的数量，有效提高了链路的可靠性。而文献［24］方法提高Rg的方法是将VNF 部署在可靠性最高的节点上，后续再不断对此进行动态调整，因此Rg也可维持在0.9 以上。文献［2］方法虽然考虑到了节点的可靠性，但却未进行聚合处理，所以Rg较低，维持在0.87 左右。对照实验方法与文献［20］方法相比，节点排序方式不同，Rg基本持平，因为两个节点排序中的限制条件并不会严重影响部署节点的数量，从而对链路的可靠性影响较低。本文方法与对照实验方法相比，VNF 聚合方式不同，Rg明显提高，说明本文的VNF 聚合方式更加有效，能够减少更多的部署节点，从而提高链路的可靠性。

图11 SFC平均可靠性Fig.11 Average SFC reliability

由图12 可看出，本文方法与文献［20］方法相比，SFC 端到端平均时延Dg降低约22%。本文方法、文献［20］方法、对照实验方法与文献［2］、文献［24］方法相比，Dg更低，因为这3 种方法都将综合时延作为评价指标对节点进行排序，同时在VNF 映射时考虑“乒乓效应”，有效地降低了链路时延，从而显著地降低了Dg。相较于文献［20］方法，对照实验方法的节点排序方式不同，Dg更低，说明用节点综合重要度对节点进行排序更加有效，能够使综合时延对节点的排序起到更加有效的作用，从而降低Dg。本文方法与对照实验方法相比，VNF 聚合方式不同，端到端平均时延更低，说明本文的VNF 聚合方式更加有效，能够减少更多的部署的节点，从而降低节点时延与链路时延，进而降低了Dg。

由图13 可看出，本文方法与文献［20］方法相比，SFC 端到端平均带宽开销Bcostave降低约29%。本文方法、文献［20］方法、对照实验方法与文献［2］、文献［24］方法相比，Bcostave更低，因为这三种方法首先进行了VNF 的聚合处理，能够显著降低带宽消耗，同时减少了链路的“乒乓效应”，能够减少链路的重复映射，从而使带宽消耗更低。对照实验方法与文献［20］方法相比，节点排序方式不同，平均带宽开销却大幅降低，说明用节点综合重要度对节点进行排序更加有效，能够让节点的跳数对于节点的排序起到更加有效的作用，从而降低Bcostave。本文方法与对照实验方法相比，VNF 聚合方式不同，平均带宽开销有所降低，说明本文的聚合方式更加有效，能够减少更多的部署节点，从而减少链路带宽消耗，降低平均带宽开销。

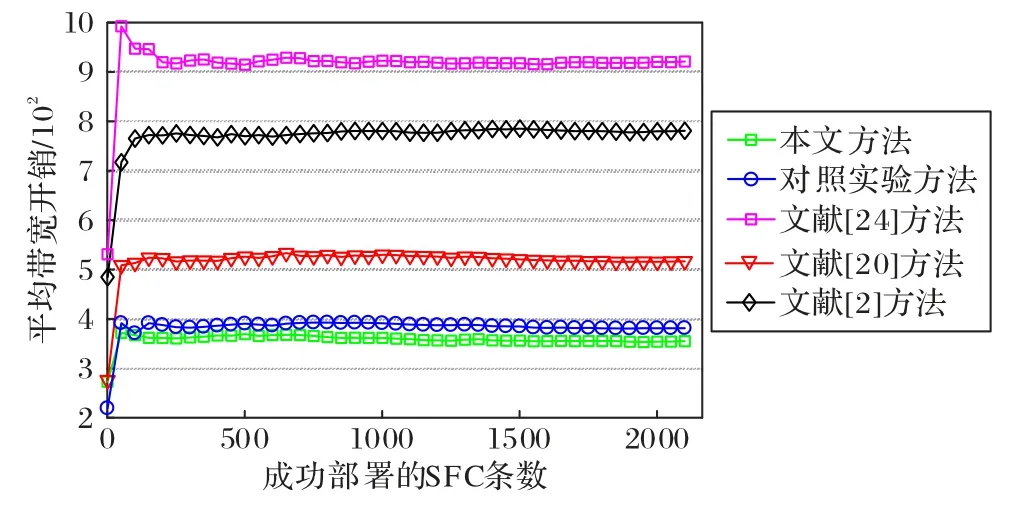
图13 平均带宽开销Fig.13 Average bandwidth overhead

4 结语

针对5G 网络环境中低时延、高可靠性的要求，本文研究了NFV 环境下关于服务功能链（SFC）的部署问题，提出了基于节点综合重要度排序的服务功能链部署方法。首先通过流量改变率将VNF 进行聚合，从而减少部署的物理节点，进而提高链路可靠性，节约节点资源消耗与链路带宽开销；然后通过节点综合重要度对节点进行排序，提高VNF 映射效率；其次将聚合后的VNF 依次映射到完成排序的底层节点上，同时在VNF 映射阶段考虑“乒乓效应”，以减少重复映射链路跳数，降低链路带宽消耗；最后通过k-最短路径算法进行虚拟链路映射，完成整个SFC 的部署。仿真结果表明，本文方法能够有效提高链路可靠性、降低时延、降低资源开销，起到了良好的优化效果。未来将结合深度学习模型对节点综合重要度的权重进行动态调整，进一步实现对SFC 的优化部署。