基于邻域重心反向学习的混合樽海鞘群蝴蝶优化算法

向君幸，吴永红

（武汉理工大学 理学院，武汉 430070）

0 引言

自然界中的许多生物系统具有高效率和鲁棒性，基于这些关键特性，学者们提出了不同的元启发式算法。元启发式算法是一种提高启发式技术性能的随机优化技术，具有简单、灵活、无衍生机制和避免局部最优等优点。种群方法近年来发展迅速，包含了著名的算法如粒子群优化算法［1］和人工蚁群算法［2］，也有新颖的算法如人工蜂群算法［3］和灰狼优化［4］。鉴于元启发式算法的优越性能，学者已成功将它们用于解决各个领域的优化问题，例如疾病诊断、查询优化、特征选择、股票预测和文本挖掘等应用。

研究发现，蝴蝶利用味觉精准地寻找到食物和同伴，并且能精确区分不同气味与强度。根据这样的特性，Arora等［5］构建了蝴蝶优化算法（Butterfly Optimization Algorithm，BOA）。相较于现有算法，BOA 具有操作简单、参数少、稳定性好的优点，并且能够很好地解决实际问题。但是在处理高维问题时，BOA 仍存在以下缺点：1）易陷入局部最优解、收敛速度较慢；2）全局和局部搜索的范围相同，只使用了非常有限的特征，没有充分利用各种特征；3）切换概率没有随着搜寻过程进行调整，导致BOA 偏离全局最优解。

为改进BOA，已有研究结合BOA 与其他方法进行优化。如：Arora等［6-7］提出二进制蝴蝶优化算法、二值蝴蝶优化算法和混沌蝴蝶优化算法，拓展了BOA 的适用领域；Singh等［8］通过增设自适应参数，提出了自适应蝴蝶优化算法等。

上述研究虽然通过不同方式改进了BOA 的性能，但也都是改进BOA 中的某个更新策略，并未有效地改进全局和局部寻优的盲目性。针对原BOA 收敛精度低和易陷入局部最优等问题，本文提出一种基于邻域重心反向学习的混合樽海鞘群蝴蝶优化算法（Hybrid Salp Swarm and Butterfly Optimization Algorithm，HSSBOA）。合理结合BOA 与樽海鞘群算法（Salp Swarm Algorithm，SSA）［9］，使两种算法各自处理全局和局部阶段，有效防止落入局部最优解。同时引入邻域重心反向学习，能够更好地帮助算法在邻域内进行搜索，提高了算法的精度。引入的动态切换概率平衡了局部搜索和全局搜索的比重，能够更加灵活地区分切换概率与产生的随机数的大小，使当前搜索阶段有了一个更合理的设定，大幅提升算法寻优能力。在10 个标准测试函数上的测试结果表明，HSSBOA 具有更高的收敛精度、收敛速度和稳定性，消融实验也验证了各项改进方法均为正向作用。最后通过选取两个工程设计的实际问题验证了HSSBOA 的应用性能，验证了HSSBOA 可用于解决实际问题。

1 蝴蝶优化算法

蝴蝶有独特的活动方式和运动轨迹。研究发现，蝴蝶利用嗅觉、视觉、味觉、触觉和听觉寻找食物和伙伴，并且可以通过气味准确定位它们的来源。根据蝴蝶的特性，Arora等［5］构建了BOA，BOA 分为以下两种情形。

1）当蝴蝶从搜索空间中最好的蝴蝶那里嗅到香气时，便飞向最好的蝴蝶，这就是BOA 的全局搜索阶段，表示如下：

其中为第i只蝴蝶第t次迭代的位置；g*为当前最优解。

2）当蝴蝶无法在搜索空间中检测到其他蝴蝶的气味时，它会随机飞行进行搜寻，此阶段为局部搜索阶段，表示如下：

式（1）、（2）中r为[0，1]中的一个随机数，它和切换概率p的大小关系决定当前进入全局搜索阶段还是局部搜索阶段。式（1）、（2）中的fi是气味感知量，由蝴蝶的感觉模态、刺激强度组成，根据模态的幂指数计算得到：

文献［5］中对BOA 的参数进行了大量的模拟实验，因此将c设为0.01；将a设为［0.1，0.3］；Ii是由目标问题（函数）计算得到的适应值。

蝴蝶通过以上构建的模型，逐步完成搜索，最终精确地寻找到气味的位置，也就是问题的最优解。

BOA 具体的步骤为：

步骤1 初始化感观模态c、幂指数a、切换概率p，并产生数量为n的蝴蝶

步骤2在下由f()得到Ii。

步骤3 通过式（3）找到最优的蝴蝶。

步骤4 从[0，1]中生成一个随机数r。

步骤5当r＜p时，通过式（1）向最优解移动；否则通过式（2）向最优解移动。

步骤6 返回步骤4，直至遍历所有种群。

步骤7 更新a的值。

步骤8 返回步骤4，直至达到最大迭代数。

2 基于邻域重心反向学习的HSSBOA

为解决BOA 易陷入局部最优解和收敛速度较慢的问题，本文从两个方面改进BOA：首先，结合BOA 与SSA，防止落入局部最优解；其次，引入动态切换概率平衡局部搜索和全局搜索的比重，更加灵活地区分切换概率与产生的随机数的大小，提升算法寻优的性能。

2.1 樽海鞘群算法及其改进

樽海鞘是一种生存于深海的海洋生物，身体呈透明的桶状，它的组织与运动方式与水母相似。通常樽海鞘以集群行动，从而通过快速协调变化和觅食实现更好的运动。Mirjalili等［9］研究了樽海鞘群的运动方式，并提出了SSA。

SSA 将种群分为领导者和追随者。领导者是种群中前段的个体，其他个体则视为追随者。领导者的更新公式为：

其中：t是当前迭代数；Maxiter是最大迭代数。

追随者的更新公式为：

其中：i≥2；代表第j维的追随者。

然而，在SSA 中，跟随者跟踪前一个个体以更新位置。这种盲目运动使解的分布过于有限，严重影响了算法的优化能力。本文使用自适应惯性权重提高算法的研究和开发能力。算法中的追随者更新方法如下：

其中：w(t)是第1 次迭代t的惯性权重，w(t)随迭代过程自适应地减小。

从式（7）可以看出，随着w(t)的减小，追随者的运动范围越来越小。在下一迭代步骤中，追随者在最后一次迭代位置的指导下执行局部优化。该策略在一定程度上提高了算法的优化能力，但是它只考虑对先行追随者行动的负面影响，忽略了先前个体的积极影响。该策略会进一步削弱先前个体的影响力，使先前个体失去更好的身体地位。

因此，本文提出自适应权重的改良方法。此方法与惯性权重的初始值和最终值以及当前迭代次数有关：当迭代次数为0，此时惯性权重为初始值；随着迭代次数的增加，惯性权重按一定比例变小；直到迭代次数最大时，惯性权重达到最终值。具体的更新公式为：

其中：ws和wf分别为惯性权重的初始值和最终值。惯性权重w(t)的取值应满足以下条件：

1）在迭代过程中，追随者当前位置和前个体位置应始终保持更新；

2）惯性权重在迭代过程中应起积极作用。

由条件1）可知：

由条件2）可知：

因此，惯性权重的取值范围应满足(0，0.5]。经过多次模拟可知，若将wf设置得过小，会导致迭代过程中惯性权重减小过快，不利于算法寻优。因此，将ws和wf分别取0.5 和0.1 的拟合结果最优。图1 给出了w(t)的迭代过程变化。

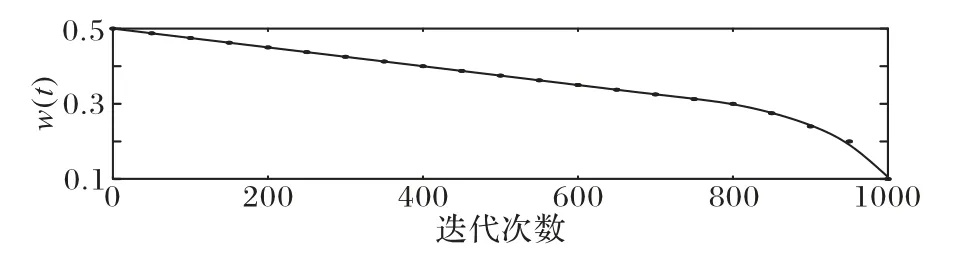
图1 权重迭代过程Fig.1 Iteration process of weight

2.2 邻域重心反向学习

反向学习是Tizhoosh［10］提出的数学模型，主要思想是通过综合评价当前解和反向解以选择一个更优解。

为了考虑更多的种群间的信息，Rahnamayan等［11］提出了重心反向点。种群的重心M定义为：

则整体中的某一点的反向点为：

为进一步拓展反向搜索的范围，提升搜寻的效率和精度，文献［12］中提出了邻域重心反向解：

其中：mi是个体i在邻域内个体的数目；k为搜索因子，是[0，1]内均匀分布的随机数。

所以可将邻域重心反向学习运用到BOA 中，将通过邻域重心反向学习得到的新解与BOA 运行后得到的解进行对比，计算公式如下：

2.3 高斯扰动

在BOA 中，个体和全局最优位置在搜索过程中会互相吸引。种群中的个体将在个体最优位置和迄今为止所有个体找到的全局最优位置之间波动。然而，当全局最优个体陷入局部最优时，其他个体会朝着全局最优个体的方向飞行，因此，在搜寻过程中会很容易陷入停滞，即陷入局部最优。

由于BOA 不能避免局部最优解，因此采用高斯扰动以提高全局搜索能力并探索搜索空间。考虑到全局和个体最佳位置的邻近区域，可以扩展它们固定位置的搜索空间，有助于整个蜂群飞到更好的位置。这种方式可以通过对全局最佳位置的高斯扰动实现。高斯分布的一维概率为：

高斯分布函数在当前位置附近产生扰动，更容易避开局部最优解，并削弱极限点的约束力。利用高斯扰动可以增加种群的多样性，提高全局搜索最优值的能力；利用高斯分布函数还可以缩短变异蝴蝶在邻域内的搜索时间；同时，利用扰动两端的突变效应，加入高斯扰动可对全局搜索进行优化。因此，改进后的BOA 具有很好的全局寻优能力。

根据以上分析，扰动项的取值应在0 附近，所以将μ的值取为0。σ可以随迭代步骤的进行而自适应：在迭代初期，为了能广泛地搜索最优解，σ的值应相对较大；随着迭代的进行，σ的值应该逐渐减小，才能搜寻较小范围内的最优解。所以σ的迭代公式为：

其中：σmax=2；σmin=1；tmax为最大迭代次数。可将式（1）改为：

2.4 动态切换概率

在BOA 中，局部和全局搜索用常量切换概率p∈[0，1]控制。一个合理的搜索过程应在算法前期进行较大范围的全局搜索，迅速定位搜索空间中全局最优解的范围。因此引入动态切换概率平衡局部和全局搜索的比重，实现更好的寻优策略。

迭代初期搜寻到的蝴蝶是最优解的概率较低，随着迭代的进行，搜寻结果是最优解的概率增加，即迭代次数和切换概率成正比。为了在初期使两个搜索阶段的可能性相等，将初始切换概率设置为0.5，将最终切换概率设置为0.8，能够让最后一次迭代有大概率搜索到全局最优的蝴蝶。因此可以构建一个p与t的线性函数，动态切换概率p如下：

2.5 算法参数设置

HSSBOA 中所有的参数如表1 所示。

表1 HSSBOA中的参数Tab.1 Parameters in HSSBOA

2.6 算法步骤

HSSBOA 的具体步骤如下：

步骤1 输入初始化感觉模态c、幂指数a、切换概率p、参数c2和c3，并产生数量为n的蝴蝶

步骤2在下由f()得到Ii。

步骤3 通过式（3）计算个体的气味，并找到最优个体。

步骤4从[0，1]中生成随机数r，计算c1与切换概率pt。

步骤5当r＜pt时，通过式（18）向最优解移动；否则通过式（7）向最优解移动。

步骤6 返回步骤4，直至遍历所有种群。

步骤7 更新a、pt、c1的值。

步骤8 生成随机数k，按式（12）计算出M，并通过式（15）进行迭代。如果新解的适应度值比原解更好，则用新解代替原来的解，否则保留原解。

步骤9 返回步骤4，直至达到最大迭代数。

2.7 算法的流程

设置算法的种群规模为N，最大迭代次数为Maxiter，维数为d。根据HSSBOA 的时间复杂度的运算规则，初始化种群的时间复杂度为O(N·d)，整个搜寻最优解的时间复杂度为O(N·d)，利用SSA 对搜索位置进行更新的时间复杂度为O(d)，故HSSBOA 总时间复杂度为O(N·d·Maxiter)。可见HSSBOA 与BOA 的时间复杂度相同，并未增加算法的负担。

3 仿真实验与结果分析

3.1 仿真实验环境

实验环境为：操作系统macOS 12.0，CPU 为Intel Core i5，主频2.3 GHz，内存8 GB，仿真软件为Matlab 2021b。

3.2 实验的初始参数设置

本文选 取BOA［5］、SSA［9］、鲸鱼优 化算法（Whale Optimization Algorithm，WOA）［13］、哈里斯 鹰算法（Harris Hawks Optimization，HHO）［14］作为HSSBOA 的比较对象。所有算法的迭代次数均设为500，种群数设为30，其他算法的参数与相应文献中的设定保持一致。

3.3 检测函数

表2 列出了本文选取的标准检测函数，其中：F1～F5为单峰检测函数；F6～F10为多峰检测函数。

表2 标准检测函数相关描述Tab.2 Description of benchmark functions

3.4 实验结果及分析

本文从收敛精度、收敛速度以及稳定性三个方面将HSSBOA 与BOA、SSA、HHO 和WOA 进行对比。在实验中，为了减小统计误差并使结果具有统计意义，每个函数独立重复30 次。实验结果如表3 中“30 维”列所示。

单峰函数只有1 个全局最优值，能够评估算法的开发能力。对于单峰函数F1～F5，HSSBOA 的平均值（mean）和标准偏差（std）都优于对比算法，在所有的单峰函数问题中都能达到理论最优值。所以，HSSBOA 在单峰函数方面具有绝对优势。BOA 和SSA 无法获得理论最优值，HHO 和WOA 则是继HSSBOA 之后最有效的算法。相较于BOA，HSSBOA 的结果更优，表明它有效地提高了BOA 的开发能力。HSSBOA 的高性能归功于在局部搜索阶段结合了SSA，因此能有效地避免陷入局部最优。

与单峰函数不同，多峰函数在搜索空间中具有多个局部最优解，可用于评估算法的探测能力。可以看出，对于多峰函数F6～F10，HSSBOA 的结果最有效并且极具竞争力，可以达到F6～F9的理论最佳值；HHO在F7～F8上达到了理论最优值，其他算法的性能从高到低依次为WOA、SSA、BOA。因此，在所有标准函数中，HSSBOA 始终是最佳的算法，表明HSSBOA在收敛精度方面具有绝对优势。

此外，还对HSSBOA 在高维数据中的性能进行了研究。将函数维度增加到500，其他参数保持不变，每个算法同样重复运行30 次。如表3 中“500 维”列所示，HSSBOA 在高维度的F1～F2以及F5～F9达到了理论最优。虽然HSSBOA在F3上的性能下降，但变化可以忽略不计。根据无免费午餐（No Free Lunch，NFL）定理［15］，没有任何算法可以解决所有优化问题，因此该结果可以接受。HHO 在高维方面不如HSSBOA，高维数据的精度均有不同程度的降低，特别是在F6和F9上有较大幅度的减小。WOA 和HHO 的精度也有显著降低。在高维度情况下，HSSBOA 整体的精度也都优于HHO 和WOA。因此，HSSBOA 的稳定性优于HHO 和WOA。

表3 标准检测函数上的实验结果Tab.3 Experimental results on benchmark functions

如图2 所示，HSSBOA对F7、F8和F10的收敛十分显著，最多只需要150 次迭代就可以收敛到最佳值。随着F1、F3和F7迭代次数的增加，HSSBOA 的收敛速度加快。虽然在F3、F4、F7和F8中HHO 的收敛速度更快，但是随着迭代过程进行，HSSBOA 能够收敛到更精确的解。在F7、F8和F10中HHO 和WOA 也能收敛到与HSSBOA 相同的解，但是可以明显看出HSSBOA 收敛的迭代次数比前两种算法要更少，因为HSSBOA 的动态切换概率加快了搜索过程。对HSSBOA 和BOA 进行进一步比较可以看出，HSSBOA 得到的拟合值更准确，并且在迭代过程中具有更快的收敛速度。这说明本文的改进方法能有效提高BOA 的收敛性能。因此，在收敛速度方面，HSSBOA 比BOA、HHO、SSA 和WOA 更具竞争力。

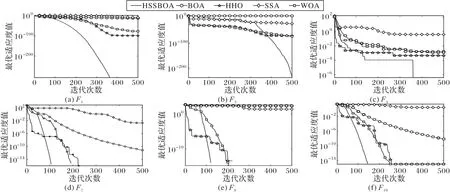
图2 收敛速度对比Fig.2 Comparison of convergence speed

3.5 Wilcoxon秩和检验

本文还进行了t检验。表4 给出了该双尾检验每个函数的t值和p值，HSSBOA 和另外算法之间的显著性水平为0.05。表5 总结了HSSBOA 和另外算法之间t检验的结果。从表5 可看出，相较于BOA、SSA，HSSBOA 在所有函数上的表现明显更优；相较于HHO、WOA，HSSBOA 在绝大部分函数上的表现更好，除了在部分函数（F7、F8、F10）上性能表现相同。因此，HSSBOA 总体上优于BOA、SSA、HHO 和WOA，拥有更高的性能。

表4 HSSBOA与其他算法的t检验比较Tab.4 Comparison of t test between HSSBOA and other algorithms

表5 t检验对比结果Tab.5 Comparison results of t-test

3.6 MAD排序

为了更好地评估HSSBOA 与4 种元启发式算法的勘探能力和收敛精度，采用平均绝对误差（Mean Absolute Error，MAE）进行排序。MAE 是一个反映算法最优值和理论最优值差距的有效统计指标，计算公式为：

其中：mi为算法取得的最优解的平均值；oi为相应的基准测试函数的理论最优值；Nf为基准测试函数个数。

各算法的MAE 排序如表6 所示。可以看出，HSSBOA 具有最小的MAE，表明了HSSBOA 的优越性。

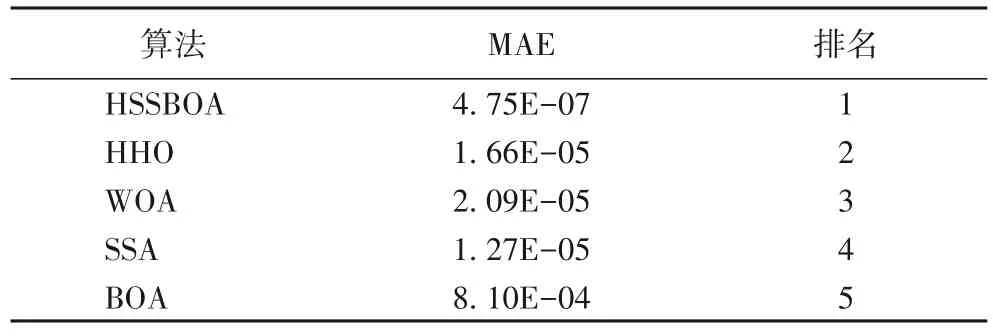
表6 HSSBOA与其他算法的MAE排序Tab.6 MAE ranking of HSSBOA and other algorithms

3.7 消融实验

为进一步验证HSSBOA 各项改进的作用和有效性，以本文所用的10 个标准检测函数为例进行消融实验，分别计算HSSBOA、HSSBOA 去除改 进SSA（记 为“HSSBOA改进SSA”）、HSSBOA 去除邻域重心反向学习（记为“HSSBOA邻域重心反向学习”）、HSSBOA 去除高斯扰动（记为“HSSBOA高斯扰动”）和HSSBOA 去除动态切换概率（记为“HSSBOA动态切换概率”）的MAE。具体结果如表7 所示。

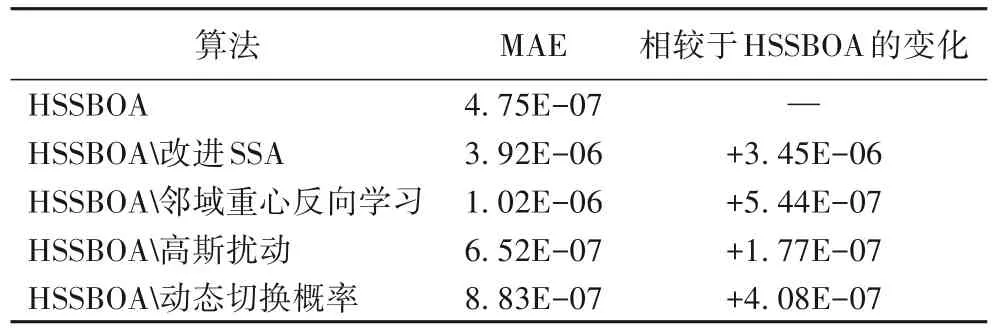
表7 消融实验的结果对比Tab.7 Comparison of ablation experimental results

通过表7 可知，将本文的4 项改进分别去除后，MAE 都有不同程度增加，说明改进的内容对算法都是正向作用。其中，改进SSA 对算法的影响最大，其次是邻域重心反向学习、动态切换概率、高斯扰动。表7 表明了HSSBOA 各项改进的合理性和有效性。

4 实际问题应用

将SSBOA 将用于测试两个工程设计问题：弹簧设计和焊接梁设计。以上数学问题可视为无约束优化问题，相对容易求解。然而，约束优化问题对于元启发式算法来说是一个挑战。因此，本文选择了几个具有代表性的多约束工程设计问题来评估HSSBOA 的性能。约束问题通常用罚函数来解决，本文采用死亡罚函数［16］来解决这些问题。

4.1 弹簧设计

此问题在于设置钢丝直径d、平均线圈直径D和移动线圈数N的值，最小化弹簧的重量，示意图如图3 所示。考虑x=(x1，x2，x3)=(d，D，N)，约束公式如下：

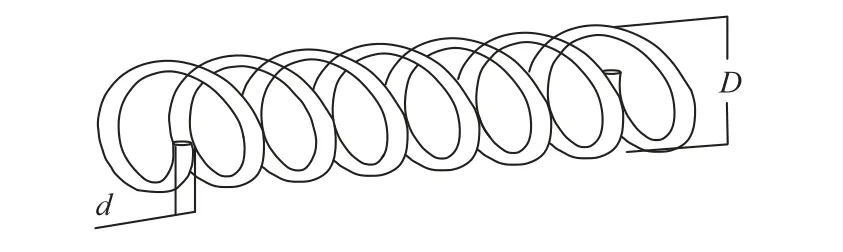
图3 弹簧示意图Fig.3 Schematic diagram of spring

其中：0.05 ≤x1≤2.00；0.25 ≤x2≤1.30；2.00 ≤x3≤15.00。

数学方法和元启发式算法都能够解决该问题。将HSSBOA 的仿真结果与其他元启发式算法以及数学方法（数学优化［17］和约束校正［18］）进行比较。如表8 所示，HSSBOA结果优于所有对比方法。

表8 各方法求解弹簧设计问题结果的比较Tab.8 Result comparison of solving spring design problem by different methods

4.2 压力容器设计

该问题的目标是使压力容器的重量最小化，如图4 所示。需要设置壳体厚度Ts、封头厚度Th、内径R、圆柱形截面长度L的值。考虑x=(x1，x2，x3，x4)=(Ts，Th，R，L)，约 束公式如下：

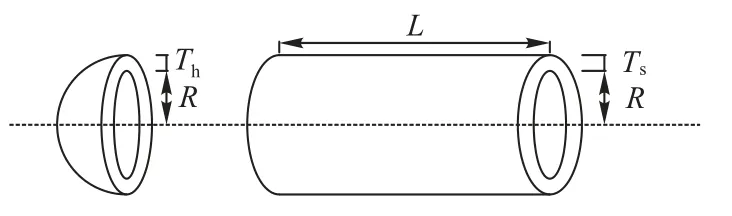
图4 压力容器示意图Fig.4 Schematic diagram of pressure vessel

其中：0 ≤x1≤99；0 ≤x2≤99；10 ≤x3≤200；10 ≤x4≤200。

将优化结果与群智能算法和数学方法（拉格朗日乘数［19］和分支界［20］）进行比较，如表9 所示。可以看出HSSBOA优于所有其他方法。

表9 不同方法求解压力容器设计问题结果的比较Tab.9 Result comparison of solving pressure vessel design problem by different methods

以上两个经典工程问题的结果表明，HSSBOA 在解决复杂和非线性问题方面具有很高的性能，可以避免局部最优，并找到有效的适应度。这些复杂问题的成功解决表明HSSBOA 具有强大的搜寻能力以及良好的收敛性能，说明HSSBOA 可以解决实际问题。

5 结语

本文提出了一种改进的蝴蝶优化算法HSSBOA，结合蝴蝶优化算法与改进的樽海鞘群算法，两种算法各自处理全局和局部阶段，能够有效防止落入局部最优中。同时还引入了邻域中心反向学习、高斯扰动和动态切换概率，平衡了局部搜索和全局搜索的比重，能够更加灵活地区分切换概率与产生的随机数的大小，提升算法寻优的性能。对10 个标准测试函数进行了仿真实验，从收敛精度、收敛速度、Wilcoxon 秩和检验、MAE 排序、高维度数据五个方面进行了分析。结果表明相较于其他群智能算法，HSSBOA 具有较好的寻优性能、较快的收敛速度以及较高的稳定性。消融实验证明了改进方法均为正向作用。此外，本文还通过两个经典工程问题验证了HSSBOA 在实际应用中的良好性能。接下来的研究方向是拓展HSSBOA 在特征选择中的应用。