多策略融合的改进黏菌算法

邱仲睿，苗 虹，曾成碧

（四川大学 电气工程学院，成都 610065）

0 引言

群智能算法是一种模拟自然界中生物群体（如蚁群、兽群、鸟群、蜂群等）集体行为的元启发式算法。这些群体在行为过程中互相交互、共享信息，通过学习彼此的经验来寻找最优的解决方案［1-3］。相较于其他优化方法，群智能算法实现较为简单，而且优化效率高。常见的群智能算法有粒子群优化（Particle Swarm Optimization，PSO）［4］、灰狼优化（Grey Wolf Optimization，GWO）［5］、黏菌算 法（Slime Mould Algorithm，SMA）［6］等。

SMA 是Li等［6］于2020 年提出的一种新型群智能算法，模拟了黏菌在寻找食物过程中形态和行为的变化。SMA 的权重系数模拟了黏菌在遇到不同浓度的食物时的生物振荡器产生的正负反馈：当找到高质量食物时，黏菌会快速靠近；当食物浓度较低时，黏菌会缓慢地向它靠近，从而以更高的效率接近最佳的食物源。SMA 代码结构简单、可扩展性强，并且在函数优化和工程设计问题上表现出色，目前已被成功应用于图像分割［7］、蛋白质序列比对［8］、机器人路径规划［9］、轴承缺陷识别［10］等领域。

然而，标准SMA 的寻优机制比较简单，它在优化高维复杂函数和最优解不在原点的函数时容易出现优化结果不稳定、收敛速度慢以及陷入局部最优等问题。针对以上问题，学者们提出了多种改进方法。Naik等［11］将平衡优化器（Equilibrium Optimizer，EO）中的平衡池机制集成于SMA 的搜索模式中，提出一种平衡黏菌算法（Equilibrium Slime Mould Algorithm，ESMA），提高了SMA 的可搜索性；Houssein等［12］将自适应引导差分进化（Adaptive Guided Differential Evolution，AGDE）算法融入标准SMA，采用AGDE 突变的方式增强种群的局部搜索能力，提高了种群的多样性，并避免SMA 过早收敛；郭雨鑫等［13］提出的改进SMA 通过引入精英反向学习提高种群的质量，并利用二次插值方法计算下一代黏菌个体的位置，提升了算法的收敛精度；Yu等［14］在SMA 的基础上集成了量子旋转门（Quantum Rotation Gate，QRG）和水循环（Water Cycle，WC）两种机制，使算法在探索和开发之间保持平衡，增强了SMA 的局部搜索能力与鲁棒性；Houssein等［15］将改进的对立学习（Modified Opposition-Based Learning，MOBL）和正交学习（Orthogonal Learning，OL）策略融入标准SMA，提高了算法的求解精度，避免了算法长时间停留在局部最优值上。

以上改进不同程度地提升了标准SMA 的优化性能，但这些方法大多是不同策略或不同算法与SMA 的简单融合，并未深入改进SMA 的位置更新公式，SMA 在求解最优解不在原点的函数时仍存在后期收敛速度慢、优化结果与最优解偏差大的问题。因此，本文提出一种多策略融合的改进黏菌算 法（Improved Slime Mould Algorithm with Multi-Strategy fusion，MSISMA）。针对SMA 求解精度低和易陷入局部最优的问题，引入布朗运动和莱维飞行策略，提升算法的搜索能力和跳出局部最优解的能力；改进黏菌的位置更新公式，将SMA 单一的位置更新机制改进为根据算法进行的阶段而变化的模式，以改善算法在探索和开发之间的过渡能力，提高算法的收敛速度和寻优精度；引入区间自适应反向学习策略，优化种群质量，提高收敛速度；加入收敛停滞监测策略，即时判断算法是否陷入收敛停滞，并对陷入停滞状态的个体进行位置初始化，帮助算法摆脱收敛停滞状态。为验证MSISMA 的有效性，选用了23 个测试函数，将MSISMA 与几种改进的SMA、标准SMA 以及几种最新的性能优越的群智能算法进行比较，同时使用Wilcoxon 秩和检验方法验证MSISMA 的有效性。实验结果表明，MSISMA 在收敛速度和求解精度上有较大的优势。

1 标准黏菌算法

黏菌算法模拟了多头绒泡菌在觅食阶段寻找食物、包围食物的过程。黏菌的前端呈扇形，后面是相互连接的静脉网络。当静脉接近食物时，黏菌的生物振荡器会产生扩散波来改变静脉中细胞质的流动，使黏菌向更好的食物移动。黏菌在接近食物阶段的位置更新公式为：

其中：Xb(t)为个体目前发现的最优解的位置；vb是范围为［-a，a］的一个随机数；W是黏菌的权重系数；XA(t)和XB(t)为从黏菌中随机选取的两个个体的位置；vc是从1 到0 递减的参数；r为[0，1]的随机数；p为决定黏菌位置更新方式的参数。p可以用以下公式表示：

其中：S(i)为第i={1，2，…，N}个黏菌个体的适应度；FD为当前迭代下黏菌的最佳适应度。

a值的更新公式如下：

其中：t为当前迭代的次数；tmax表示最大迭代次数。

权重系数W模拟了黏菌在遇到不同浓度的食物时生物振荡器的振荡频率的变化：

其中：r为[0，1]的随机数；Fb和Fw为当前迭代过程中的最佳适应度和最差适应度；SmellIndex表示个体适应度S按升序排列（在最大值问题中按降序排列）后的个体位置索引。

黏菌在寻找食物的过程中也会分割一部分个体进行随机探索。综合上述理论，黏菌的位置更新公式为：

其中：BU和BL是搜索范围的上限和下限；rand和r为[0，1]区间的随机数；z是决定随机分布的黏菌个体占黏菌总体的比例的参数，z=0.03。

2 多策略融合的改进黏菌算法

SMA 是一个简单有效的算法，有一定的寻优能力，但仍有几点不足：

1）从黏菌位置更新机制来看，在标准SMA 中，黏菌位置的更新规则由r、p、z三者的大小关系决定。当r＜p时，黏菌的位置更新由当前最优个体的位置和两个随机个体的位置决定，此时黏菌表现为在当前最佳位置附近随机探索。这增强了SMA 前期的全局搜索能力，但无目的的随机探索也会使SMA 的前期收敛速度变慢。随着迭代次数增加，黏菌种群会向当前最佳位置靠拢，使SMA 在求解具有多个局部最优值的函数时极易陷入局部最优。当r≥p时，黏菌的位置更新由收敛因子vc和黏菌个体的自身位置决定。随着迭代次数增加，vc从1 线性收敛到0，使黏菌种群的位置向原点方向收敛。这种位置更新方式不利于最优解不在原点的函数的优化，在优化这类函数时，标准SMA 的求解精度较差。

2）SMA的z参数是一个很小的常数，随机分布的黏菌个体占总个体的比例很小，SMA 在陷入局部最优时缺乏有效的跳出局部最优的机制。

3）SMA 的寻优机制较简单，在平衡算法的探索和开发能力上还有较大的提升空间。

针对以上问题，本文提出了多策略融合的改进黏菌算法（MSISMA），在以下方面作出改进：1）引用布朗运动和莱维飞行机制，增加黏菌个体分布的多样性，增强黏菌在局部区域探索的能力；2）改进黏菌的位置更新策略，使算法在不同阶段采用不同的位置更新公式，平衡算法在探索和开发之间的过渡能力；3）采用区间自适应的反向学习策略，增加黏菌分布的多样性，优化黏菌个体的质量；4）引入收敛停滞监测策略，动态监测算法是否陷入收敛停滞，当监测到算法处于停滞状态时，该策略会对部分个体的位置重新初始化，避免算法长时间处于收敛停滞状态。

2.1 布朗运动与莱维飞行

2.1.1 标准布朗运动

布朗运动是一种无规则的随机游走过程，已被研究者们广泛用于群智能算法的设计及改进，以提升算法的搜索性能。沙林秀等［16］提出一种基于布朗运动与梯度信息的交替优化算法（Alternately Optimizing Algorithm based on Brownianmovement and Gradient-information，AOABG），在算法全局搜索阶段加入布朗运动机制，使种群以最优个体的位置为中心作布朗运动，增强了算法的全局搜索能力。汤安迪等［17］在麻雀搜索算法的基础上引入布朗运动，增强了算法的全局探索能力，并有助于算法脱离局部最优状态。在标准SMA 的前期迭代过程中，黏菌个体容易快速向当前种群的最佳位置靠近，导致算法的全局探索能力较差，难以找到全局最优解。本文将标准布朗运动引入MSISMA 迭代前期的位置更新公式中，增加黏菌个体的位置的多样性，从而提高算法的全局探索能力。

标准布朗运动的步长由均值为0（μ=0）、方差为1（σ2=1）的正态分布概率密度函数决定：

引入布朗运动后的黏菌位置更新公式为：

其中：XC(t)为在适应度排序为前N/3 的个体中随机选取的个体的位置；α为步长控制因子；RB为布朗运动步长。由式（8）可知，在黏菌的基本位置更新公式上加入布朗运动，可增强黏菌个体的搜索轨迹的随机性，进而增强算法的搜索能力。

2.1.2 莱维飞行

在标准SMA 中，随着算法进入迭代后期，黏菌个体的位置分布趋于集中，SMA 容易陷入局部最优，导致收敛停滞。莱维飞行是一种步长服从莱维分布的随机游走，它的运动方式既有小范围的游走，也有大距离的跨越。莱维飞行已被广泛用于优化算法领域，例如帝王蝶优化（Monarch Butterfly Optimization，MBO）［18］和哈里 斯鹰优化器（Harris Hawks Optimizer，HHO）［19］都在种群位置更新公式上引入莱维飞行机制，有效地提升了算法的寻优效果。Mantegna［20］于1994年提出了一种生成莱维分布随机数的算法，莱维飞行步长s的计算方式如下：

u和v服从均值为0、方差分别为σu、σv的正态分布：

其中：β取值为1.5。

本文使用文献［20］中的算法模拟莱维飞行，并将莱维飞行引入MSISMA 迭代后期的位置更新公式中，使黏菌个体保持它的位置的活跃性，增加黏菌个体跳出局部极值的概率，从而有效改善标准SMA 在迭代后期易陷入局部最优的缺陷。改进后的黏菌位置更新公式表示如下：

其中：X(t)为t次迭代时黏菌的位置；δ为步长控制因子；RL为莱维飞行步长。

2.2 黏菌位置更新的改进

在标准SMA 中，黏菌的寻优过程主要由当前最佳个体和两个随机个体的位置引导，寻优机制比较单一。在迭代初期，下一代黏菌种群的位置受两个随机个体的位置的影响，使SMA 全局搜索的效果较差，前期收敛速度较慢；在迭代后期，黏菌种群的位置受收敛因子vc的影响而向原点方向移动，当优化问题的最优解不在原点时，SMA 的寻优过程会受到干扰，导致算法收敛精度较差。为改善SMA 在前期探索和后期开发之间的过渡过程，提高SMA 在迭代前期的收敛速度，优化求解精度，本文改进黏菌位置的更新公式，将位置更新过程划分为三个阶段。

1）阶段1。

2）阶段2。

3）阶段3。

在阶段1，r＜p时，黏菌种群位置更新由当前最佳个体和一个随机个体的位置引导，位置更新模式表现为以当前最佳个体为中心的放射性扩散，阶段1 在保证算法的全局搜索能力的同时加快了种群向最优个体移动的过程，以提升算法在前期的收敛速度。在阶段2，rand≥z时，黏菌种群位置更新由当前最佳个体和适应度排在前N/3 的一个随机个体的位置引导，此时种群的搜索轨迹在较优个体所在的区域内；同时在基本位置更新公式上加入了布朗运动，以增强算法在较优个体附近的搜索能力。在阶段3，rand≥z时，种群位置更新由当前最佳个体和本体的位置引导，此时种群在最佳个体附近进行局部搜索，以提高算法在迭代后期的寻优精度，加入的莱维飞行机制则给算法提供了跳出局部最优的能力。此外，在三个阶段，rand＜z时会对黏菌个体的位置重新随机，从而使黏菌种群在算法的整个迭代过程都具有多样性。

2.3 区间自适应反向学习策略

Tizhoosh［21］于2005 年提出了一种反向学习（Opposition-Based Learning，OBL）方法以提升算法的寻优效率。该方法首先计算当前解的反向解，然后将反向解与当前解进行比较，最后保留两者中更接近最优解的一项用于下次的迭代计算。反向点的定义如下：

定义1反向点。D维空间内有一点h=(x1，x2，…，xD)，且x1，x2，…，xD∈R，xi∈[ai，bi]，i={1，2，…，D}，则h点的反向点为

设优化问题为求解最小值，优化问题的函数为f(x)，当前解为h，反向解为，则解的保留策略为：

其中：t为当前迭代数。

传统OBL 方法计算反向解时，边界ai和bi是固定值，生成的反向解的质量可能较差。因此本文提出一种区间自适应反向学习（Interval Adaptative Opposition-Based Learning，IAOBL）策略优化反向学习的边界，进一步提高反向解的质量。IAOBL的反向解计算公式如下：

其中：i={1，2，…，D}；j={1，2，…，N}；D为求解问题维度；N为种群个体数；t为当前迭代数。IAOBL 策略中的上下边界随算法迭代的进行不断变化，当种群集中到某区域时，生成反向解的上下边界也在不断缩小。将IAOBL 引入标准SMA中，有助于提升黏菌种群的整体质量，加快算法的收敛进度。

2.4 收敛停滞监测策略

SMA 在迭代过程中会遇到收敛速度变慢，甚至收敛停滞的情况。为了识别并改善这种情况，本文提出一种收敛停滞监测策略，具体方案如下。

步骤1设gc为算法t次迭代与t-3 次迭代的适应度差值：

其中：t={ 4，5，…，tmax}；tmax为最大迭代次数。

步骤2设gmin为适应度监测因子：

其中：t={4，5，…，tmax}。

步骤3 比较gc与gmin的大小关系，如果gc＜gmin，则视为算法收敛停滞，即对1/3 的黏菌个体进行位置重新随机的操作：

收敛停滞策略能实时监测算法的收敛状态，判断算法是否停止收敛，并在算法进入收敛停滞状态时对部分种群进行重新初始化，从而增加黏菌个体分布的多样性，避免算法长时间处于收敛停滞状态。

2.5 算法具体流程

MSISMA 首先对种群的位置进行初始化，并计算所有个体的适应度和权重系数；然后判断算法所处的阶段，根据不同阶段选择不同的位置更新策略；随后应用IAOBL 策略生成反向种群，通过解的保留策略对当前种群和反向种群中的个体进行选择和保留；最后通过收敛停滞监测策略判断算法是否处于收敛停滞，如果算法处于停滞状态则对部分个体的位置再进行初始化。MSISMA 的具体步骤如下：

步骤1 算法参数初始化。设置黏菌个体数N，问题维度D，最大迭代次数tmax，搜索边界BU和BL，黏菌的位置X。

步骤2 计算每个个体的适应度，并对适应度进行排序，记录最佳适应度Fb和最差适应度Fw。

步骤3 根据式（4）更新黏菌的权重系数W。

步骤4 根据式（13）～（15）更新黏菌个体的位置。

步骤5 根据式（17）生成当前种群的反向种群，并根据式（16）决定要保留的个体。

步骤6 根据式（20）对陷入搜索停滞的黏菌个体进行位置重新随机。

步骤7 迭代次数加1，判断结束条件，若满足，则算法终止，输出最佳适应度及对应位置；若没有，则返回步骤2。

2.6 时间复杂度分析

设黏菌种群规模为N，问题维度为D，迭代次数为tmax，则MSISMA 的时间复杂度分析如下。

步骤1 黏菌种群的位置初始化阶段需要进行D次运算，时间复杂度为O(D)。

步骤2 计算每个黏菌个体的适应度，时间复杂度为O(N)。对所有黏菌个体的适应度进行排序，时间复杂度为O(N× logN)。

步骤3 计算所有黏菌个体的权重系数，时间复杂度为O(N×D)。

步骤4 更新黏菌个体的位置，时间复杂度为O(N×D)。

步骤5 根据当前黏菌种群的位置生成反向种群，时间复杂度为O(D)。比较当前黏菌种群和反向种群的适应度值，判断要保留的个体。此过程需要进行N次判断，时间复杂度为O(N)。

步骤6 判断算法是否处于收敛停滞状态，需要1 次计算，时间复杂度为O(1)。若满足收敛停滞监测条件，则对部分黏菌个体的位置进行重新随机，时间复杂度为O(N/3)。

所以在满足收敛停滞监测条件时，MSISMA 的总体时间复杂度为O（D+T（7/3×N+D+N·logN+2ND+1））；不满足收敛停滞监测条件时，MSISMA 的总体时间复杂度为O（D+T（2N+D+N·logN+2ND+1））。标准SMA 的时间复杂度主要是黏菌种群的位置初始化、适应度计算、适应度排序、权重系数更新以及种群的位置更新，时间复杂度计算为：O（D+T（N+N·logN+2ND）。相较于标准SMA，MSISMA 的时间复杂度最大增加了O（T（4/3×N+D+1））。而2TND远大于T（4/3×N+D+1），所以MSISMA 与标准SMA 的时间复杂度大致相同。

3 实验与结果分析

3.1 实验环境

本次仿真实验环境如下：CPU 为Intel Core i7-10750H，主频2.60 GHz；32 GB 内存；Windows 10（64 位）操作系统；运行软件为Matlab R2021b 64 位。

3.2 测试函数

本节使用了文献［22］中的23 个基准函数对算法的性能进行测试。其中：f1～f7为多维的单峰函数，这类函数只有一个最小值，因此可以测试算法的收敛速度；f8～f13为多维的多峰函数，这类函数存在多个局部极小值，并且局部极小值的数量随维度的增加呈指数增长，这类函数可以测试算法定位全局最优解和摆脱局部最优的能力；f14～f23为固定维的多峰函数，这类函数的局部极小值数量较少。

3.3 对比算法及参数设置

为验证本文的多策略改进黏菌算法（MSISMA）的有效性，将MSISMA 与平衡黏菌算法（ESMA）［11］、黏菌-自适应引导差分进化混合算法（Slime Mould Algorithm combined to Adaptive Guided Differential Evolution，SMA-AGDE）［12］、SMA［6］以及最近提出的海洋捕食者算法（Marine Predators Algorithm，MPA）［23］和平衡优化器（EO）［24］这5 种算法进行比较。为了比较的公平性，设置所有算法的种群规模N=30，维度D=30，最大迭代次数tmax=500，运行次数Times=30。各算法的内部参数设置如表1 所示。

表1 各算法的参数设置Tab.1 Parameter setting for each algorithm

3.4 测试函数实验结果与分析

所有算法在每个测试函数上独立运行30 次，记录下每次运行后的优化结果，然后计算30 次运行结果的平均值（Avg）和标准差（Std），得到结果如表2 所示。

由表2 可以看出，相较于其他算法，MSISMA 在19 个测试函数上获得了最佳平均值，在12 个测试函数上获得了最佳标准差值。相较于ESMA、SMA-AGDE、SMA、MPA 和EO，MSISMA 的优化精度平均提高了26.04%、55.97%、36.79%、23.39%和54.18%。

表2 不同算法的测试函数优化结果Tab.2 Test functions optimization results of different algorithms

对于单峰函数f1～f7，MSISMA 在求解f1～f4时的每次运行都能取得函数的全局最优解；对于f5，MSISMA 的求解精度最高，并且标准差最小；MSISMA 求解f6的结果仅次于MPA，但要优于其他改进的SMA；对于f7，MSISMA 计算的平均值和标准差仅次于ESMA。从单峰函数优化结果来看，MSISMA 的表现优于对比算法，且MSISMA 的标准差很小，说明算法有较好的鲁棒性。对于可变维多峰函数f8～f13，MSISMA 的优化精度最高，且标准差最小。特别是在函数f8、f12、f13的优化上，MSISMA 明显优于其他算法。说明MSISMA 解决了SMA 在求解具有多个局部最优解的函数时优化精度不高、容易陷入局部最优的问题。对于f14、f16～f19，MSISMA 的求解精度最高，接近函数的最小值，但标准差不如MPA；对于f15，MSISMA 的优化精度比MPA、EO 差，但优于ESMA、SMA-AGDE 和SMA；对于f20，MSISMA 的表现较差；对于f21、f22和f23，MSISMA 的优化精度提升比较明显，优化平均值与函数的全局最优值非常接近。综合来看，MSISMA 无论是在优化精度还是算法的鲁棒性上相较于对比算法都更有优势。

为了更直观地比较各个算法的收敛速度和求解精度，图1 给出了算法运行30 次后部分测试函数的平均收敛曲线。对于单峰函数f1和f2，MSISMA 的收敛速度最快，能够以最快速度收敛到函数的最优值；对于单峰函数f5，MSISMA 的收敛速度最快，运算精度最高，而且没有在迭代过程中陷入局部最优。对于多峰函数f8、f10、f12、f14和f21，MSISMA 无论是收敛速度还是最后的优化结果都有明显的优势。

图1 部分测试函数收敛曲线对比Fig.1 Comparison of convergence curves of some test functions

3.5 Wilcoxon秩和检验

为了进一步评估MSISMA 的性能，本文使用Wilcoxon 秩和检验方法来检验MSISMA 和对比算法的运行结果是否有显著性差别。显著性水平设置为0.05，将所有算法运行30次的优化结果作为样本。当检验的p值大于0.05 时，说明两种算法的运行结果没有显著差异；否则，两种算法运行结果存在显著差异。表3 为MSISMA 与对比算法的Wilcoxon 秩和检验结果。

由表3 可知，MSISMA 在17 个测试函数上的表现优于ESMA 与SMA，在19 个测试函数上表现优于SMA-AGDE，在12 个测试函数上的表现优于MPA，在16 个测试函数上表现优于EO。因此MSISMA 的性能在统计上有显著的优越性。

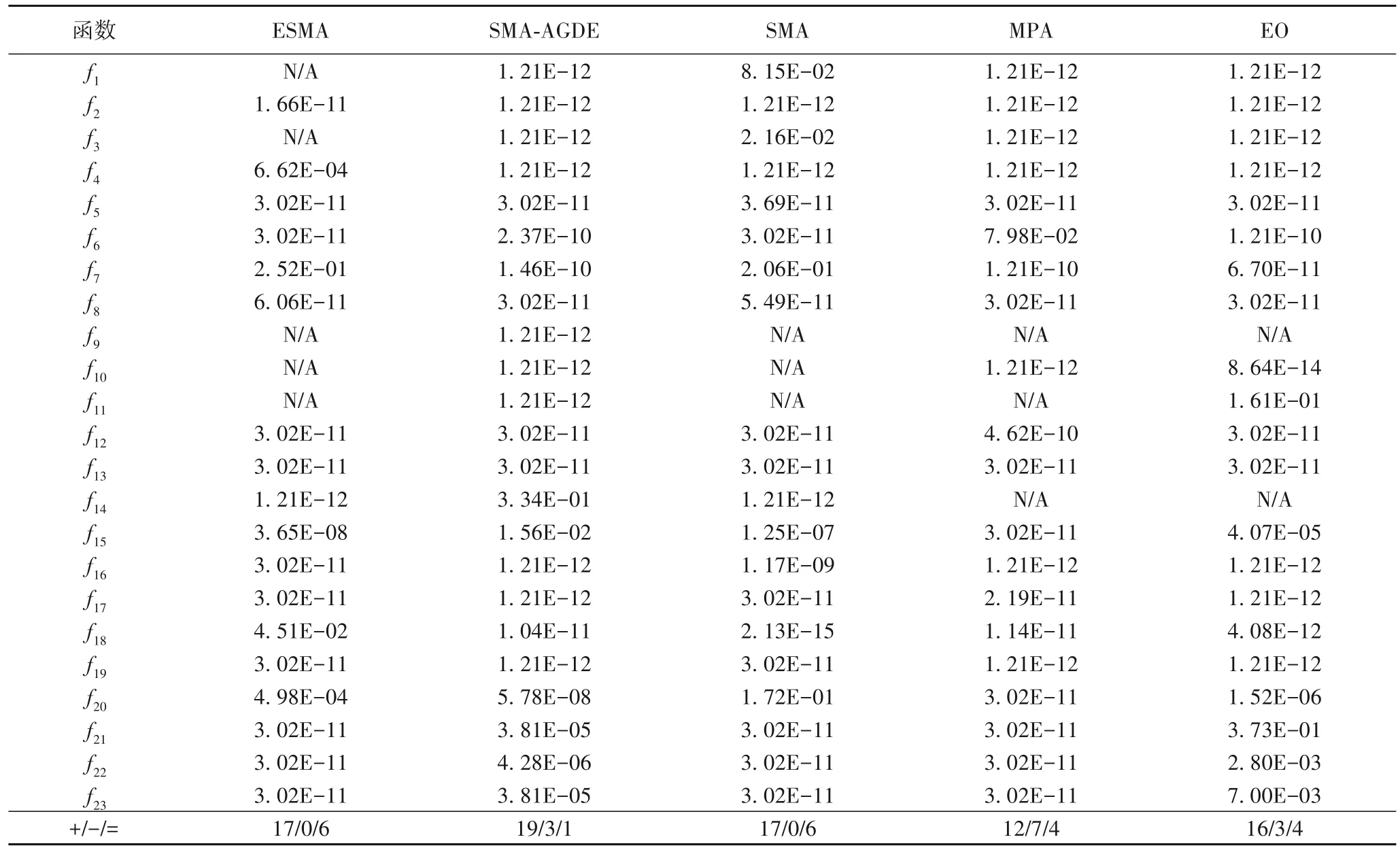
表3 Wilcoxon秩和检验结果Tab.3 Wilcoxon rank-sum test results

实验结果表明，本文提出的多策略融合的改进黏菌算法的收敛速度、求解精度和鲁棒性都有明显提升。

4 结语

为了提高黏菌算法的优化性能，本文提出了一种多策略融合的改进黏菌算法（MSISMA）。引入布朗运动和莱维飞行机制增强算法的搜索能力；改进算法的位置更新公式，以平衡算法在探索和开发之间的过渡能力，提升寻优效率和精度；引入区间自适应的反向学习策略，优化解的质量；引入收敛停滞监测策略，避免算法长时间处于收敛停滞状态。在测试函数上的实验结果表明，MSISMA 在收敛速度、寻优精度和鲁棒性上比ESMA、SMA-AGDE、SMA、MPA 和EO 更优秀。然而，MSISMA 在优化某些固定维的多峰函数时仍存在精度较低的情况，未来将在种群位置更新模式方面作进一步研究和优化。