一道2021年中考几何作图题的解法探究

南京二十九中教育集团初级中学 庄 历

中学数学教育不仅要让学生获得必要的数学知识和技能，还要能让学生感悟数学的基本思想，积累数学思维活动和实践活动的经验.学生解题能力的高低，不仅可以反映其基本知识、基本技能的掌握情况，更可以反映其综合能力水平.而学生在解题实践中，常常无法找到解题的入口，不能搭建已知条件和未知结论之间的有效桥梁.因此，教师分析问题时的引导过程就显得尤为重要，只有从学生的主动思维渐渐推导出所有的可知和需知，找到连接可知和需知之间常用的模型支撑，才能教会学生正确的思考方法，积累探索问题的途径.本文中以2021年南京市中考中的一道几何作图题为例，通过对条件和结论的分析，以及对多种解法的探索，积累基本几何模型，提高学生的解题能力和综合分析能力.

1 题目呈现

图1

原题(2021年南京市中考第25题)如图1，已知P是⊙O外一点，用两种不同的方法过点P作⊙O的一条切线.要求:(1)用直尺和圆规作图;(2)保留作图的痕迹，写出必要的文字说明.

2 追本溯源

本题是教师和学生都非常熟悉的一道几何作图题，在苏科版九年级上册“对称图形——圆”这一章教授直线与圆的位置关系时，很多教师喜欢用它引入“切线长定理”，但由于新授课教学目标和时间分配的问题，课堂上对于解法没做过多的探究.新授课时，根据学生的最近发展区，因为他们刚刚学完“圆周角定理”和“直线与圆的位置关系”，所以最容易想到的就是利用“直径所对的圆周角等于90°”来构造垂直，从而利用“经过半径外端点并且垂直于这条半径的直线是圆的切线”证明作法的正确性.

3 解法探究

图2

首先根据结论画出目标图形，理清已知条件和未知结论，探寻它们之间的联系，找到突破口.要想过点P作⊙O的一条切线，根据切线的判定，如图2，既可以在⊙O上确定一点A，使得PA⊥OA，即∠PAO=90°，也可过点O向过点P的某直线作垂线，使垂线段的长等于⊙O的半径.

3.1 “90°角的构造”，探究多种方法

利用切线的第一种判定方法时，对于构造直角，学生并不陌生，在中考复习阶段，教师完全可以引导学生找到多个思考角度：

①直径所对的圆周角等于90°；

②“直角三角形斜边上的中线等于斜边一半”的逆命题；

③等腰三角形的“三线合一”；

④矩形的每个内角为直角；

⑤菱形的对角线互相垂直平分；

⑥全等三角形对应角相等.

切入点1：利用“直径所对的圆周角等于90°”.

作法一：(1)作PO的垂直平分线交PO于点B；

(2)以B为圆心，BO为半径作⊙B交⊙O于点A；

(3)连接PA，则直线PA即为所求切线，如图3.

图4

切入点2：利用“直角三角形斜边上的中线等于斜边一半”的逆命题.

作法二：同作法一，如图4.

理由简述：因为BP=BA，BA=BO，

所以∠BPA=∠BAP,∠BAO=∠BOA.

又在△APO中，

∠BPA+∠BAP+∠BAO+∠BOA=180°.

所以∠PAO=∠PAB+∠BAO=90°.

切入点3：利用“矩形的每个内角为直角”.

作法三：(1)作PO的垂直平分线交PO于点B;

(2)以B为圆心，BO为半径作⊙B交⊙O于点A，交AB的延长线于点C;

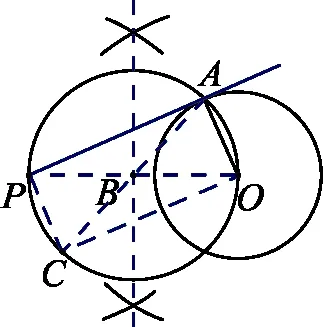
图5

(3)连接PA，则直线PA即为所求切线，如图5.

理由简述：∵BP=BO，BC=BA，

∴四边形APCO为平行四边形.

又BP+BO=BC+BA，即PO=AC，

∴平行四边形APCO为矩形.

∴∠PAO=90°.

以上三种作法虽然类似，但是构造的基本模型却不相同.通过不同的切入点，调动学生对几何图形的认知，从而“无中生有”构造出不同的基本模型，最后又神奇地统一为类似的作法，让学生深入了解几何模型之间的联系，对构建学生的图形与几何板块的知识结构有很大的帮助.

切入点4：利用等腰三角形的“三线合一”.

作法四：(1)连接PO并延长，交⊙O于点B，C；

(2)以P为圆心，PO为半径画弧，以O为圆心，BC为半径画弧，两弧交于点D；

(3)连接OD交⊙O于点A；

图6

(4)连接PA，则直线PA即为所求切线，如图6.

理由简述：因为PD=PO，DA=AO=r(记⊙O半径为r)，所以PA⊥DO.

切入点5：利用“菱形的对角线互相垂直，C；

作法五：(1)连接PO并延长，交⊙O于点B，C；

(2)以P为圆心，PO为半径画弧，以O为圆心，BC为半径画弧，两弧交于点D，分别以D，O为圆心，PO为半径画弧，两弧交于点E；

图7

(3)连接PE，DO交于点A，则直线PA即为所求切线，如图7.

理由简述：因为PD=PO=OE=DE， 所以四边形DPOE为菱形.

故OA=AD=r，OA⊥PA.

切入点6：利用“全等三角形对应角相等”.

作法六：(1)在任一直线MN上取点C，过点C作GC⊥MN；

(2)在CG上截取CD=OB；

(3)以D为圆心，PO为半径画弧，交MN于点E；

(4)以P为圆心，CE为半径画弧，交⊙O于点A，画直线PA，则直线PA即为所求切线，如图8.

图8

图9

理由简述：易证△CDE≌△AOP(SSS).

所以∠PAO=∠ECD= 90°.

对于切入点6，也可以直接在原图中，借助半径OB来构造全等三角形，方法类似，如图9：

3.2 “线段的构造”，探究多种方法

3.2.1 构造半径OA

除了连半径，证垂直，同样可以考虑作垂直，证半径.对于确定线段OA的长度，可以从以下几个角度来考虑：①全等三角形对应边相等； ②相似三角形对应边成比例.

切入点7：利用“全等三角形对应边相等”.

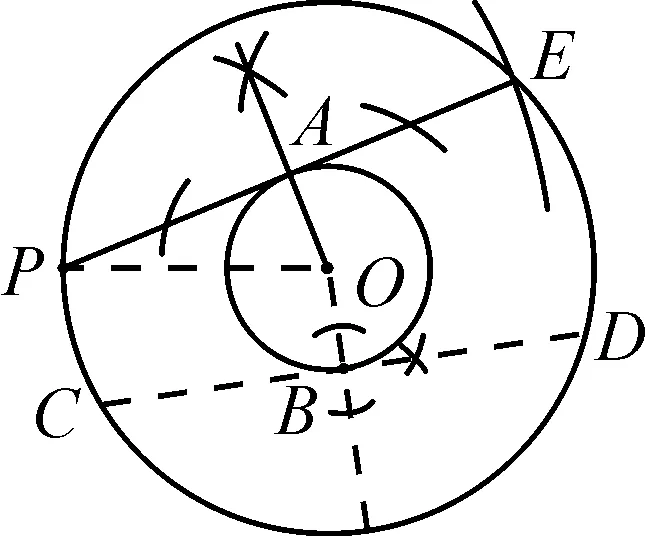
图10

作法七：(1)如图10，以O为圆心，OP为半径画大⊙O；

(2)在小⊙O上任取一点B，连接OB，过点B作OB的垂线，交大⊙O于点C，D；

(3)以P为圆心，CD为半径画弧，交大⊙O于点E；

(4)连接PE，过点O作OA⊥PE于点A，则直线PA即为所求切线.

又因为PE=CD，所以BC=AP.

易证△OBC≌△OAP(HL)，则有OA=OB=r.

切入点8：利用“相似三角形对应边成比例”.

谈到相似三角形，大家最容易想到的是“A”字型，我们可以构造一个相似比为1∶2的“A”字模型.

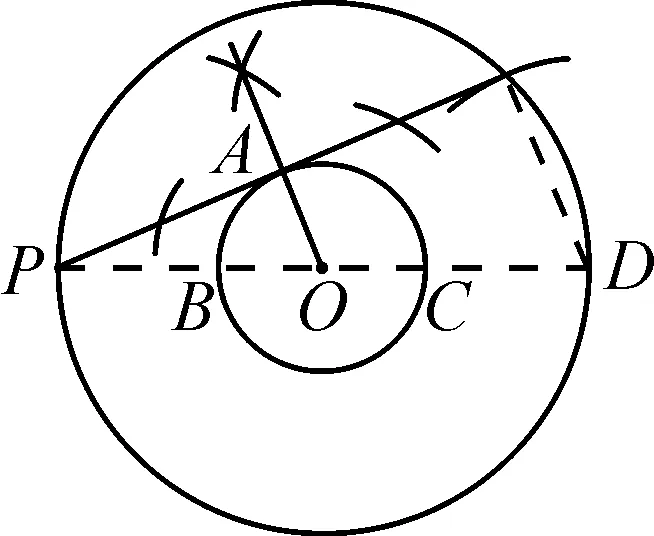
图11

作法八：(1)如图11， 以O为圆心，OP为半径画大⊙O；

(2)连接PO并延长，交小⊙O于点B，C，交大⊙O于点D；

(3)以D为圆心，BC为半径画弧，交大⊙O于点E；

(4)连接PE，过点O作OA⊥PE于点A，则直线PA即为所求切线.

理由简述：∵PD为大⊙O的直径，且OA⊥PE，

∴∠PAO=∠PED=90°，则OA∥DE.

∴△PAO∽△PED.

图12

作法九：(1)如图12， 作PO的垂直平分线交PO于点C；

(2)作PC的垂直平分线交PC于点D，以D为圆心，PD为半径画⊙D；

(3)作BO的垂直平分线交BO于点E，以C为圆心，OE为半径画弧交⊙D于点F；

(4)画直线PF，过点O作OA⊥PF于点A，则直线PA即为所求切线.

理由简述：∵PC为⊙D的直径，且OA⊥PF，

∴∠PFC=∠PAO=90°.

即FC∥OA.

∴△PAO∽△PFC.

∴OA=2FC=r.

作法九的思路虽然和作法八类似，都是构造“A”字型从而完成90°的转化，但是作法九明显要比作法八复杂.

3.2.2 构造线段PA

不管是连半径，证垂直，还是作垂直，证半径，都可以完全确定直角三角形PAO，除了通过确定∠PAO或者OA来完全确定直角三角形PAO，还可以尝试确定PA的长度.

切入点9：利用“相似三角形对应边成比例”.

如图13，我们知道△PAC∽△PBA，从而可以得到PA2=PB·PC，这里PB和PC都是定值，如何确定PA的长度？这一等式让我们联想起了“射影定理”.如图14，在直角三角形EPC中，有PE2=PB·PC，也有EB2=PB·BC.那么，我们只需借助PB和PC构造“母子三角形”，即可确定PA的长度.

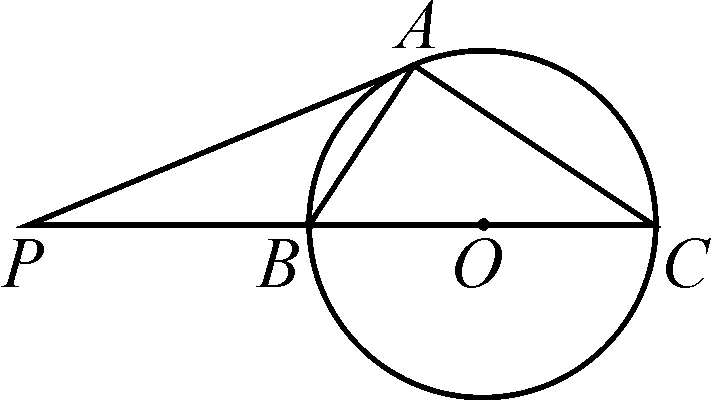
图13

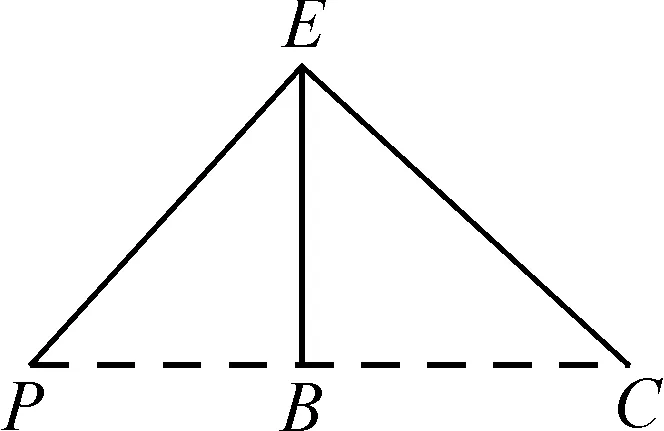
图14

作法十：(1)如图15，连接PO并延长，交⊙O于点B，C；

图15

(2)作PC的垂直平分线交PC于点D；

(3)以D为圆心，PD为半径画⊙D；

(4)过点B作PC的垂线交⊙D于点E；

(5)以P为圆心，PE为半径画弧交⊙O于点A；

(6)画直线PA，则直线PA即为所求切线.

4 反思

尺规作图是学生在图形与几何中要掌握的重要技能，需要学生综合运用所学知识，多角度思考问题，并借助五种基本尺规作图，完成整个构图过程.这不仅需要学生熟练掌握五种基本尺规作图，更需要灵活运用初中的几何模型.

本题解法很多，但细细想来，主要还是分两条主线，那就是切线的两种判定方法：作半径，证垂直；作垂直，证半径.根据这两条主线，分别唤醒学生已有的几何模型储备，建立直角模型的构造体系和线段的构造方法.

这道几何作图题，可以放在中考一轮复习“圆”这一章，这样不仅可以帮助学生复习证明切线的两种方法，更可以激发学生思维的火花，在探寻多种方法的同时，帮助学生复习构造直角和线段的多种方法，让学生对几何图形中基本元素的构造有更多的认识.