拼图 直观 思考*
——以数学实验“玩转方块纸”为例
江苏省苏州工业园区东沙湖实验中学 葛善成 李明树
《义务教育数学课程标准(2011版)》指出:“课程内容的选择要贴近学生的实际,有利于学生体验和理解、思考与探索……要重视直观,处理好直观与抽象的关系.”[1]七年级学生好动、好奇、好表现,采用形象生动的数学实验教学有利于激发学生的学习兴趣,有利于学生广泛、积极主动地参与学习.
1 教学案例
1.1 创设情境,激发兴趣
播放微视频,了解几何形体画派创始人蒙德里安及其作品;欣赏蒙德里安晚期的代表作《红、黄、蓝的构成》(如图1).

图1
师:你能从这幅作品中发现什么?
生1:长方形、正方形,水平线、垂直线,等等.
师:很好!看来你也有成为数学家的潜质.
师:事实上,数学家发现如果一个正方形的边长是整数,那么它就可以被分割成有限个边长为1的小正方形.大家同意吗?
生(众):同意.
师:举个例子,如果正方形的边长是5,那么它可以被分割成多少个边长为1的小正方形?
生2:25个.
师:有没有可能分割成26个正方形?
生3:不可能.
设计意图:通过欣赏艺术作品,学生既可以体会艺术来源于数学,发展自身的审美趣味,感悟数学的文化价值,同时又为用图形法证明无理数奠定逻辑基础(即一个边长是整数的正方形可以被分割成有限个边长为1的小正方形).
1.2 问题探究,建构模型
问题1计算1+2+3+4+……+99+100.
生4:由错位相加法,可知
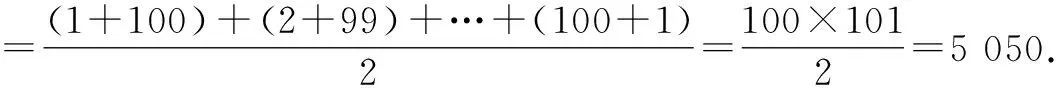
师:非常棒!还有其他做法吗?
生5:分组相加,原式=(1+100)+(2+99)+……+(50+51)=101×50=5 050.
师:很好!我们还可以从“形”的角度研究这个算式,加数1可以用1个小方块表示,加数2可以用两个小方块表示……,把这些小方块拼在一起(如图2).
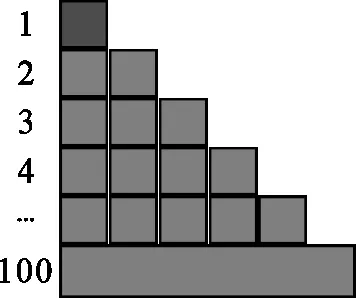
图2
师:这幅图形像什么呢?
生6:梯形、三角形、阶梯……
师:这个图形与算式的和有什么关系呢?
生7:图形中小方块的数量就是算式的和.
生8:图形的面积就是算式的和.
师:很好!那如何求这个图形的面积呢?
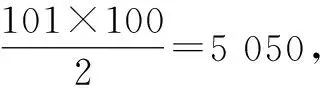
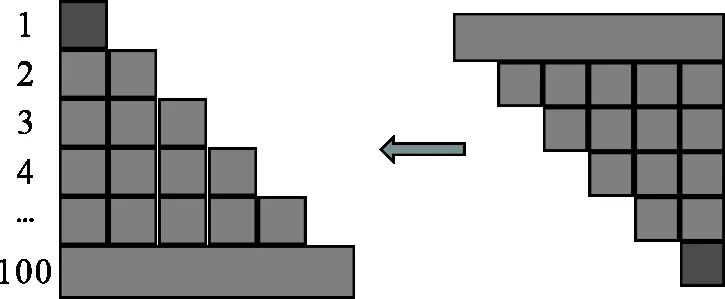
图3
师:非常好!借助方块纸把原算式转化成“阶梯形”,再用拼图法求“阶梯形”的面积,求出原算式的和,那么你能求1+2+3+……+(n-1)+n的和吗?
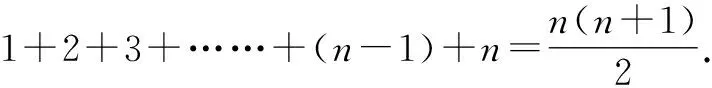
师:很好!那么你能用类似的方法解决问题2吗?
设计意图:引导学生从形的角度思考,探索方块纸的摆放规律,感受数与形之间存在的一定关联,为学生更好地理解求和问题提供了直观便捷的途径.
问题2计算1+3+5+7+……+(2n-1).

图4
生11:把这些小方块拼成一个大正方形(如图4),大正方形的边长为n,所以大正方形的面积为n2,即原式=n2.

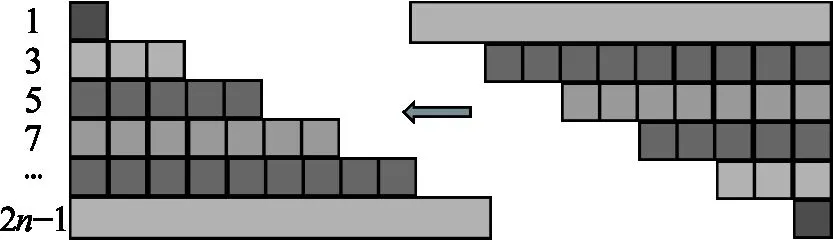
图5
师:非常棒!那么接下来可以算什么?
生13:连续的偶数和.
师:很好!自己动手操作试试看.(略)
设计意图:在问题1的基础上,探究连续奇数和的拼图规律,学生在充分尝试、猜想、调整、再探究之后展示方案,进而解决连续偶数的和问题.帮助学生抓住利用拼图求和的本质,培养学生思维的连贯性和深刻性.
1.3 类比迁移,深度探究
问题3计算:12+22+32+……+n2.
生14:我由问题2联想到每一个加数都对应着一个“阶梯形”(如图6),然后把这些“阶梯形”拼成一个规则图形求面积,但好像拼不了.

图6
师:把这些“阶梯形”每一层剪开,然后在KT板上拼一拼,试试看.
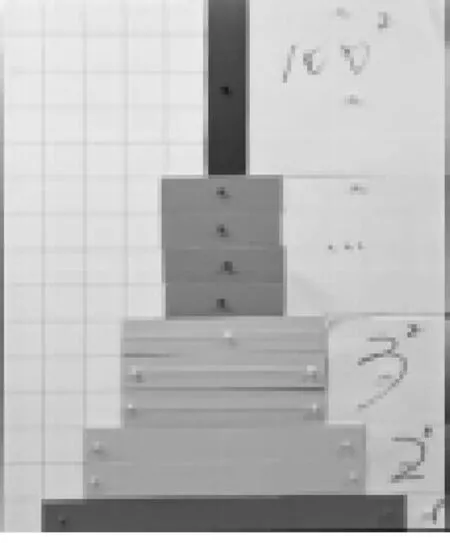
图7
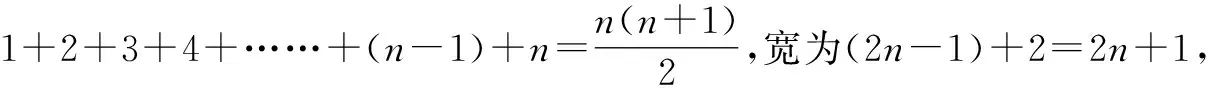
设计意图:问题3的思维层次较高,具有一定的挑战性.引导学生用前面积累的活动经验,将抽象的算式具体化、形象化,分析不同拼图方案的可行性,使其经历自主探究、合作交流并形成数学模型的过程.
问题4计算:13+23+33+43+……+n3.
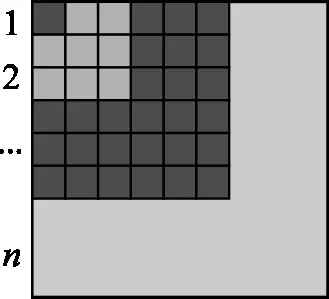
图8
师:小组合作,动手操作.
师:还有其他思路吗?
生17:用小立方体拼图……(略)
设计意图:问题4的设计遵循了由低到高、螺旋递进的原则,基于前面的经验积累,学生的抽象思维能力得到了提升,解决该问题的方案也多样化.对于学生的各种方案,可鼓励学生在课后继续探究.
1.4 回归课本,启思明理
师:这里有两个边长为1的小正方形,你能把它们剪拼成一个大正方形吗?
生18:可以,如图9.

图9
师:大正方形的面积是多少呢?
生19:大正方形是由两个面积为1的小正方形拼成,所以大正方形面积为2.
师:如果设大正方形边长为a,那么a是多少呢?
生20:好像是无理数.
问题5 若a2=2,则a是有理数吗?
(众生疑惑.)

图10

生21:图10中,两个未重合的小正方形面积之和等于重合的大正方形面积.
生22:重合的大正方形和未重合的两个小正方形边长分别是2n-m,m-n,都是整数.
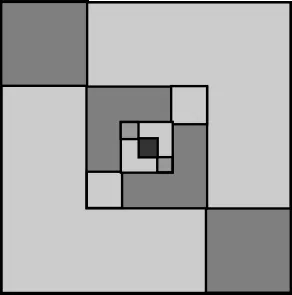
图11
生23:这个过程可以无限迭代,原大正方形可以无限分割(如图11)下去,最终会有某一个小正方形的边长小于1,这与“一个边长是整数的正方形可以被分割成有限个边长为1的小正方形”这一常识不符,所以假设是不成立的,即a是无理数.
师:非常棒!你能用类似的方法判断——若a2=3,则a是有理数吗?(略)
设计意图:无理数对七年级学生而言是一个非常抽象难懂的概念,首先通过拼图让学生感受无理数的客观存在,其次由于用有理数逼近无理数的过程算不完、算不尽,学生的接受程度并不高,通过无限拼图,将抽象的无理数证明直观化,彰显从实践操作到极限思维的升华,提升学生数学思维品质.
1.5 交流收获,课堂小结
让学生交流本节课的收获.
2 教学反思
2.1 在拼图中启思
数学的发展历程表明,越是高度抽象的数学内容,往往越需要形象直观的模型作为其解释和支撑.在数学教学中运用适当的图形或直观的模型能够帮助学生启发思路,理解抽象的数学知识,有利于学生的思维向更高级、更抽象的方向发展,自然数的求和问题对学生来说比较抽象,为突破这一难点,笔者以具身认识理论为指导,借助于方块纸设计拼图实验,启发学生主动思考.将算式中的加数用方块纸表示,那么算式的和就转化成所有方块纸的面积和,那么如何求方块纸的面积和呢?启发学生把方块纸拼成有规律的图形.基于以上的活动经验,学生甚至可以在“头脑”中拼图,求出连续偶数的和.通过动手操作、动脑思考的拼图,启发学生自主探究,体验和感受数学结论发现和再创造的过程,进而培养学生主动发现、提出问题,分析、解决问题的能力.
2.2 在直观中明理
几何直观有助于学生直观地理解数学,在培养学生创新能力和提升数学素养等方面影响深远.实践证明,数学实验是培养学生几何直观素养的有效载体,具有独特的作用和价值.笔者利用方块纸进行拼图实验培养学生体验操作的习惯,在实验中自然地发展学生几何直观素养.例如,问题5在直观操作的基础上,将直观与简单推理相结合,从图形的角度证明a是无理数,简洁但不失逻辑的严密性.学生在实验中经历观察、分析、交流、猜想、归纳等创造性的思维过程,构建方块纸无限分割的直观模型,从中感受到数与形的联系,获得过程性的知识.探索证明这一类无理数的思路使得操作与推理得到统一,拓展了学生思维生长的空间.
2.3 在思考中发展
笔者借助方块纸这一直观素材诱发学生的直观思维,引导学生动手“做”数学,启发学生的智力因素和非智力因素参与探究,达到启思的目的.探究的过程虽然不是严格的数学证明,但学生在“做”数学过程中的简单推理,就是明理的过程.其中,方块纸拼图是教学明线,正是因为方块纸的介入,使相对枯燥的数学问题变得有趣、有意义,让抽象的思考过程变得可视化.借助直观启发思考、积累基本活动经验则是教学暗线,如在问题1的引领下,借助方块纸拼图求连续奇数和、连续偶数和、连续自然数的立方和显得并不困难,甚至可在“头脑”中想象拼图,做到把“做数学”和“想数学”结合在一起,体现手脑协同的理念.在明暗结合、启思明理中引导学生用数学的眼光观察世界,用数学的思维思考世界,把握数学内容的本质,以简驭繁,为学生的持续发展和终身学习创造条件.

