抛体运动常见考点赏析

■华中科技大学附属中学 许 文

将物体以一定的初速度抛出,物体只在重力(或恒力)作用下的运动称为抛体运动,抛体运动是一种典型的匀变速曲线运动。抛体运动可分为平抛(类平抛)运动与斜抛运动。求解抛体运动问题需要用到运动的合成与分解的思想方法,具备建构物理模型的能力,空间想象能力,应用数学知识处理物理问题的能力,以及定性分析与定量研究相结合的分析能力等。下面梳理抛体运动的常见考点,预测2023年高考对抛体运动的考查方向,供同学们参考。

一、抛体运动的分类与研究方法

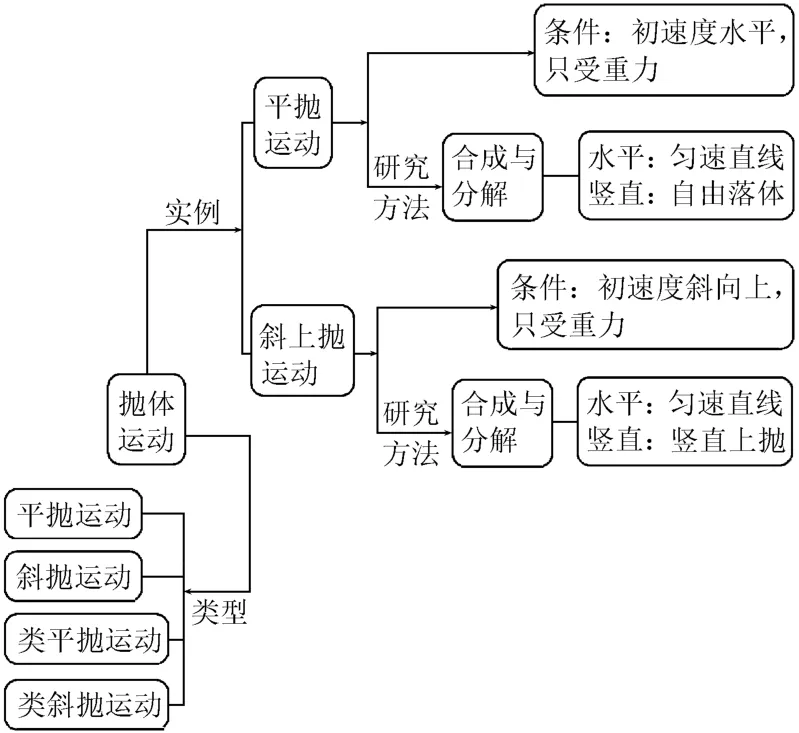
二、抛体运动考点例析

1.平抛运动的规律。

设做平抛运动物体的水平初速度大小为v0,下落高度为h,重力加速度为g,其基本规律如表1所示。

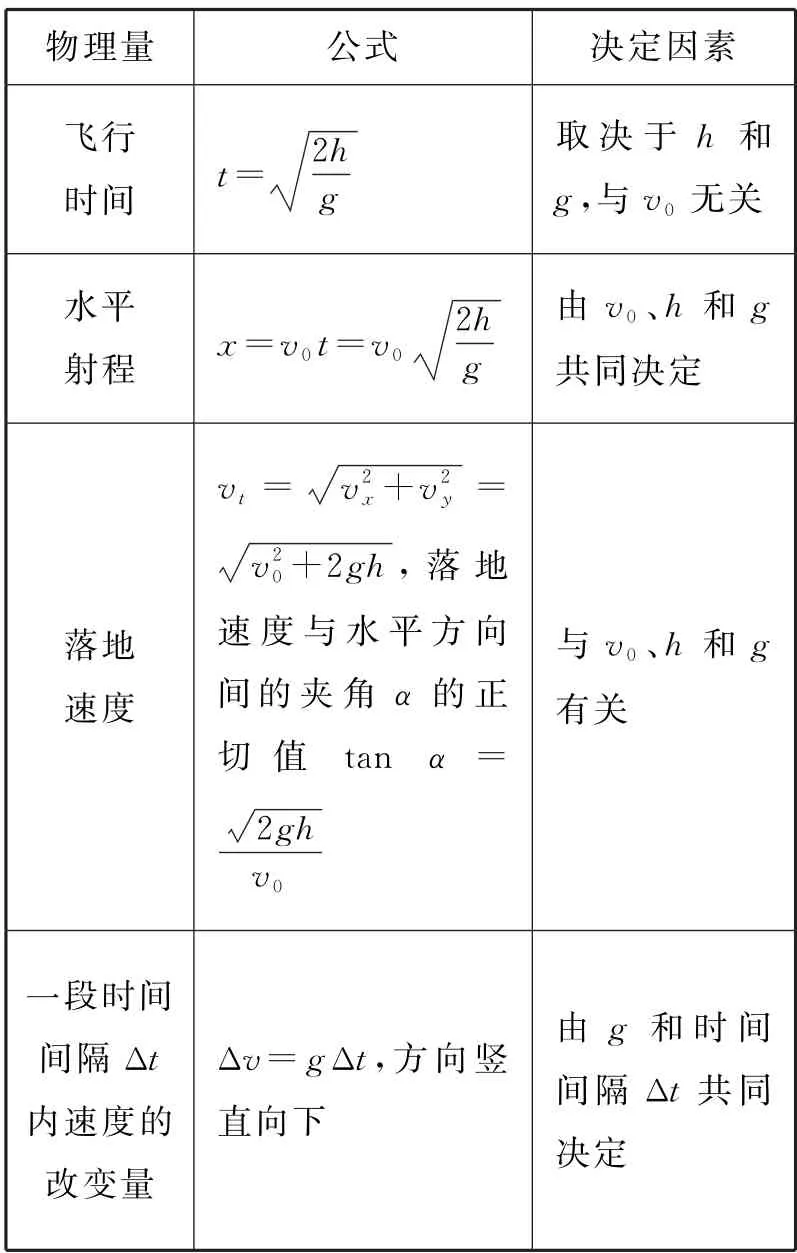
表1

例1(2022年高考广东卷)如图1所示,在竖直平面内,截面为三角形的小积木悬挂在离地足够高处,一玩具枪的枪口与小积木上P点等高且相距为L。当玩具子弹以水平速度v从枪口向P点射出时,小积木恰好由静止释放,子弹从射出至击中积木所用时间为t。不计空气阻力。下列关于子弹的说法中正确的是( )。

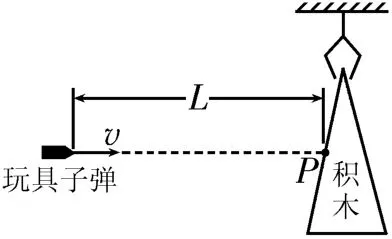
图1

A.将击中P点,

B.将击中P点,

C.将击中P点上方,

D.将击中P点下方,

解析：玩具枪的枪口与P点等高,玩具子弹和小积木在竖直方向上均做自由落体运动,当子弹击中积木时,子弹和积木的运动时间相同,均为t,根据平抛运动规律可得,子弹和积木的下落高度均为,因此子弹将击中P点。根据平抛运动规律得L=vt,因此子弹从射出至击中积木所用的时间t=。

答案：B

点评:平抛运动可以看成水平方向上的匀速直线运动和竖直方向上的自由落体运动的合运动,处理平抛运动问题的方法就是沿水平和竖直两个方向进行运动的分解,把曲线运动转化为两个直线运动,再根据直线运动规律列式求解。本题中玩具子弹从枪口射出至击中积木的过程中做平抛运动,子弹在水平方向上的位移等于L,根据匀速直线运动规律得L=vt,子弹在竖直方向上的位移;积木由静止释放后做自由落体运动,其位移等于子弹在竖直方向上的位移h。

2.平抛运动的约束。

几种常见的有约束的平抛运动类型示例如表2所示。

表2

例2如图2所示,科考队员站在半径R=10 m 的半圆形陨石坑(直径水平)边,沿水平方向向坑中抛出一石子(视为质点),连接石子在坑中的落点P与圆心O,OP连线与水平方向间的夹角θ=37°。已知石子的抛出点在半圆形陨石坑左端的正上方,且到半圆形陨石坑左端的高度h=1.2 m。取重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8,不计空气阻力。石子抛出时的速度大小为( )。

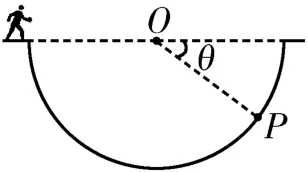
图2

A.9 m/s B.12 m/s

C.15 m/s D.18 m/s

解析：石子在竖直方向上做自由落体运动,根据几何关系得石子的下落高度H=h+Rsinθ,根据平抛运动规律得,解得t=1.2 s。石子在水平方向上做匀速直线运动,根据几何关系得石子的水平射程x=R+Rcosθ,根据平抛运动规律得x=v0t,解得v0=15 m/s。

答案：C

点评:求解有约束的平抛运动问题,需要灵活运用平抛运动的位移和速度分解方法,结合约束面(斜面、圆弧面等)的特点,找出相应的几何关系。找出平抛运动满足的几何关系这一重要的隐含条件是问题得以顺利求解的前提。

3.平抛运动的推论。

(1)做平抛(或类平抛)运动的物体任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图3所示,A、B两点对应的水平位移满足。

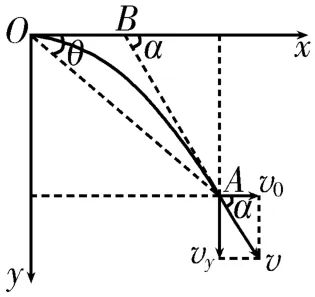
图3

(2)设做平抛(或类平抛)运动的物体在任意时刻任意位置处的速度方向与水平方向间的夹角为α,位移方向与水平方向间的夹角为θ,则tanα=2tanθ。

例3如图4所示,半径为R的半球形碗固定在水平面上,碗口水平,AB为直径,O点为球心。将一弹性小球(可视为质点)从AO连线上的某点C沿CO连线方向以某初速度抛出,经过时间(g为重力加速度)小球与碗内壁第一次碰撞后恰好返回C点。假设小球与碗内壁碰撞前后瞬间小球的切向速度不变,法向速度等大反向。不计空气阻力,则C、O两点间的距离为( )。

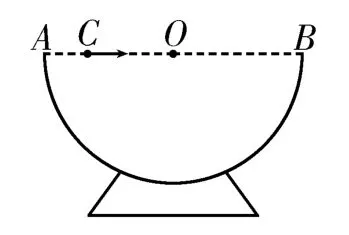
图4

解析：小球从C点以某初速度水平向右抛出,要使小球能反弹回C点,小球必须垂直打在碗内壁上。如图5所示,设碰撞点为D,连接OD,即为小球做平抛运动的轨迹过D点的切线。过D点作DE⊥AB于E点,则O点为小球水平位移的中点,根据平抛运动规律得,根据平抛运动的推论得xCO=xOE,在Rt△ODE中有R2,解得。

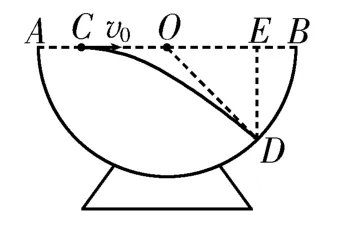
图5

答案：C

例4跳台滑雪是冬奥会中极具观赏性的项目之一。如图6所示,一滑雪坡道由上斜坡A1B、圆弧面BC、竖直台阶CD和倾角为θ的下斜坡DE连接而成,且圆弧面末端C处切线水平。某运动员第一次从上斜坡的A1点由静止滑下通过C点后飞落到下斜坡DE上,第二次从上斜坡的A2点由静止滑下通过C点后也飞落到下斜坡DE上。设该运动员两次与下斜坡DE接触时速度方向与水平方向间的夹角分别为β1和β2,不计空气阻力和坡道的摩擦力,则( )。

图6

A.β1＞β2

B.β1＜β2

C.β1=β2

D.无法确定β1和β2的大小关系

解析：连接C点与运动员第一次在下斜坡DE上的落点,如图7所示。根据平抛运动的推论得tanβ1=2tanα1,同理得tanβ2=2tanα2,又有α1＜α2,故β1＜β2。

图7

答案：B

点评:求解有斜面约束的平抛运动问题,需要充分运用斜面倾角,找出斜面倾角与位移偏向角、速度偏向角的关系;求解有曲面约束的平抛运动问题,灵活应用平抛运动的两个推论可以达到快速解题的目的。

4.斜抛运动的分析方法。

斜上抛运动从抛出点到最高点的运动可逆向看成平抛运动,分析完整的斜上抛运动需要根据对称性处理。

例5(2022年高考山东卷)如图8所示,某同学将离地1.25 m 的网球以13 m/s的速度斜向上击出,击球点到竖直墙壁的距离为4.8 m。当网球的竖直分速度为零时,击中墙壁上离地高度为8.45 m 的P点。网球与墙壁碰撞后,垂直于墙面的速度分量大小变为碰前的0.75倍,平行于墙面的速度分量大小不变。取重力加速度g=10 m/s2,网球碰墙后的速度大小v和着地点到墙壁的距离d分别为( )。

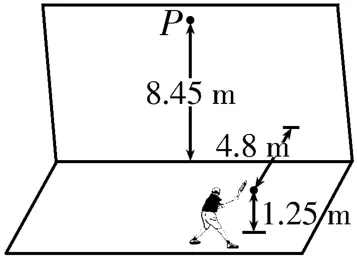
图8

A.v=5 m/s B.

C.d=3.6 m D.d=3.9 m

解析：网球从被击出到击中P点的运动过程可逆向看成平抛运动,根据平抛运动规律可得,网球被击出时沿竖直方向的初速度大小,沿水平方向的初速度大小,其中H=8.45 m,h=1.25 m,v0=13 m/s,解得v0y=12 m/s,v0x=5 m/s。网球被击出时与P点间的水平距离x0=v0xt1,其中,解得x0=6 m。如图9所示,设网球的水平位移x0与墙面间的夹角为θ,根据数学知识得,其中x=4.8 m,则sinθ=0.8,即θ=53°。网球击中P点时平行于墙面的速度分量v1=v0xcosθ=3 m/s,垂直于墙面的速度分量v2=v0xsinθ=4m/s。网球碰墙后垂直于墙面的速度分量v2'=0.75v2=3 m/s,平行于墙面的速度分量v1'=v1=3 m/s,故网球碰墙后的速度大小,选项A 错误,B正确。网球着地点到墙壁的距离d=,选项C错误,D 正确。

图9

答案：BD

点评:将斜上抛运动的初速度沿水平方向与竖直方向分解,斜上抛运动可视为水平方向上的匀速直线运动与竖直上抛运动的合运动。斜上抛运动在最高点时的速度沿水平方向,通过逆向思维可将斜上抛运动从抛出点到最高点的运动处理为平抛运动研究,从而降低解题的难度。注意:本题中网球的运动是三维空间内的有约束斜抛运动,找出空间几何关系是正确求解的关键。

总之,高考对抛体运动的考查以平抛运动为主,兼顾斜抛运动,求解这类问题时需要从抛体运动的性质特征、能量转化、分解方法、约束类型、临界极值等角度出发全面考虑。同学们在复习备考的过程中要重点掌握抛体运动的研究方法与基本规律,构建问题情景,灵活运用相关数学知识分析物理问题。

1.打乒乓球是一种大家喜闻乐见的体育运动,它对场地要求低且容易上手。某同学疫情期间在家锻炼时,对着墙壁练习打乒乓球,球拍每次击球后,球都从同一位置斜向上飞出,其中有两次球在不同高度分别垂直撞在竖直墙壁上。不计空气阻力,则这两次球从飞出到撞击墙壁前( )。

A.飞出时的速度大小可能相等

B.飞出时的速度竖直分量可能相等

C.在空中运动的时间可能相等

D.撞击墙壁时的速度可能相等

2.如图10所示,A、B两球在地面O点上方的同一竖直线上的不同位置,A、B两球间的距离h=5 m,分别给两球水平向右的初速度,使两球做平抛运动,结果两球的运动轨迹相交于C点,OC连线与竖直方向间的夹角θ=53°,A、B两球的初速度大小分别为v1=3 m/s,v2=5 m/s,已知sin 53°=0.8,cos 53°=0.6,取重力加速度g=10 m/s2,不计空气阻力。设A、B两球从抛出点运动到C点所用的时间分别为t1和t2,A、B两球抛出时离地面的高度分别为h1和h2,则( )。

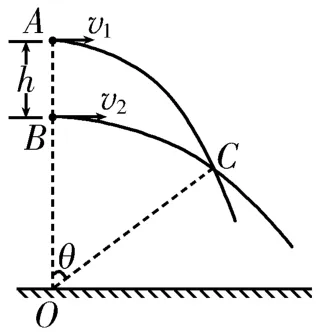
图10

A.t2=1.25 s

B.t2=0.75 s,

C.t2=1.25 s,

D.t2=0.75 s,

3.如图11所示,在足球比赛的一次罚点球中,主罚运动员在球门前罚球点将球打入球门右上角,球沿水平方向入网。设球门宽为L,高为h,罚球点与球场底线中点相距为a。不计空气阻力,则球的初速度方向与水平面间的夹角θ满足( )。

图11

4.(2022年6月浙江高考卷)如图12所示,带等量异种电荷的两正对平行金属板M、N间存在匀强电场,板长为L(不考虑边界效应)。t=0 时刻,M板中点处的粒子源发射两个速度大小为v0的相同粒子,垂直于M板向右的粒子,到达N板时的速度大小为;平行于M板向下的粒子,刚好从N板下端射出。不计重力和粒子间的相互作用,则( )。

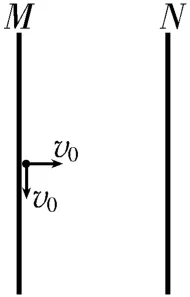
图12

A.M板电势高于N板电势

B.两个粒子的电势能都增加

D.从N板下端射出的粒子在电场中运动的时间

5.某游戏装置如图13所示,安装在竖直轨道AB上的弹射器可上下移动,能水平向右射出速度大小可调节的小弹丸。圆心为O的圆弧槽BCD上开有小孔P,弹丸落到小孔时,其速度只有沿OP连线方向才能通过小孔,游戏过关,则下列判断中正确的是( )。

图13

A.弹射器位于B点时,只要弹丸射出时的速度合适就能过关

B.弹射器在轨道上的位置只要高于B点,弹丸射出时的速度合适都能过关

C.弹射器在轨道上的位置只有一个,且弹丸以某一速度射出才能过关

D.弹射器在轨道上的位置有两个,只要弹丸射出时的速度合适都能过关

参考答案：1.A 2.D 3.A 4.C 5.C