常用排序算法性能分析平台的设计及结果分析＊

强振平，肖晨亮，李时雨，李俊萩

(西南林业大学大数据与智能工程学院，云南 昆明 650224)

0 引言

排序是计算机科学的重要内容，是计算机及相关专业的学生必须掌握的一类基础算法[1]。排序算法的应用[2,3]有很多，常见的有插入排序、选择排序、交换排序和归并排序等多种排序方法。

在“数据结构”课程教学中，一般要求学生将数据结构与算法的理论运用到编程实践中，让学生体会数据结构在实际应用中的重要作用[4]。而由于“数据结构”课程的描述大多是抽象形式，实现过程多以简单示例为主，造成学生的学习困难。这就对“数据结构”课程的实验教学提出了更高的要求，学生需要通过编写程序代码将所学的理论知识融会贯通。对于排序算法，教师通过设计实验，使得学生能够对不同排序算法的特点深入理解，重视编程逻辑思维的培养，在遇到实际问题时，合理地选择排序算法[5]。因此，本文从不同等级的数据量、不同初始排序序列的数据为出发点设计排序实验，并对常用排序算法的执行时间、比较次数和移动次数进行分析比较，直观地反映各种排序算法优缺点，对学生深刻地认识和理解排序算法有着重要的意义。

1 排序算法简介

1.1 排序的基本概念

关键字[6]：关键字是数据元素（或记录）中某个数据项的值，用它可以标识一个数据元素（或记录）。

排序[7]：按关键字的非递减或非递增顺序对一组数据重新进行排列的操作。

排序的稳定性[7]：若排序前后关键字相同的数据相对位置不发生变化，则称所用的排序算法是稳定的，否则就是不稳定的。

1.2 排序算法分类

按照排序方式的不同，常用的排序算法可分为四类（如图1所示），按照每类排序算法的思想，又包括一些不同算法，本文针对这四类中八个具体的算法进行分析。

图1 常用排序算法分类

首先，对各类排序算法的实现原理进行简略说明（以升序为例）。

⑴插入排序，先把原序列分为有序子序列（开始时只有一个数据元素）和无序子序列，然后每轮循环从无序序列中取出一个数据元素，插入到有序子序列的合适位置，直到无序子序列为空为止。

⑵选择排序，先把原序列分为有序子序列（开始时为空）和无序子序列，循环从未排序子序列中选出最小数据元素加入到有序子序列中。

⑶交换排序：把原序列分为有序子序列（初始为空）和无序子序列，循环将每个数据交换到正确位置。

⑷归并排序：采用分而治之的思想，依次将两个或两个以上的有序序列合并成一个有序序列。其中，最常用的就是二路归并排序，即将一个待排序的序列分成两个序列，分别对这两个序列排序。而对于这两个序列排序的方式也是将这两个序列分别分成两个序列分别排序。

根据不同排序算法的实现原理和实现步骤，可以推导出各排序算法的时间复杂度，空间复杂度及稳定性等性质。参见表1。

表1 常见排序算法的性质对比

虽然几乎所有的教材都给出类似于表1 的结果，但是对于学生来讲，各种算法的具体执行性能依然不够直观，实用情况也不清楚。基于此，我们设计了常用排序算法性能分析平台。

2 实验平台设计

为了更加直观地感受不同排序算法在不同待排序数据情况下的执行效率以及发现哪些因素是影响排序算法执行效率的关键因素。实验实现八种排序算法，并用不同数据规模和不同初始化排序状态的待排序数据进行实验，将每次算法的执行时间、比较次数和移动次数记录并进行可视化分析。实验平台的设计思路如图2所示。

图2 排序算法比较实验平台设计思路

执行程序时，需要从控制台输入待排序的数据规模和选择随机、正序或逆序生成待排序的数据元素，程序会在执行每个排序函数之前对数据进行恢复，保证每个排序函数对相同的数据进行排序，满足比较的公平性。所有排序方法执行完毕后，控制台打印每个排序算法的执行时间、比较次数和移动次数。同时将输出数据写入文件，便于进一步可视化分析。

实验过程采用了基于x86_64架构服务器，CPU 为Intel Xeon E5-2683V3 2.00GHz，运行内存64GB，采用Ubuntu操作系统，版本号为16.04.1。采用C 语言对8 种排序算法进行了编程实现，其中代码已尽可能精简，减少冗余。完整的代码可以在https://github.com/qzplucky/SortCompare下载。

3 排序算法性能分析比较

通过变量确定数据元素数量和数据初始化状态（包括了随机、正序和逆序三种方式），在确定的数据初始状态下分析多种数据规模时每种算法的执行效率，得出在该数据状态下不同算法的优劣；相同的数据排序时，分析排序时间与比较次数和移动次数的关系；在相同的数据规模时，分析哪种排序算法的排序效率更容易受到数据初始状态的影响。

3.1 随机初始化状态下不同数据规模各种排序算法的时间效率

在实际工作中，需要排序的数据绝大部分情况下满足随机分布（可以认为是无序的），因而无序状态下排序算法的效率最能体现出该算法的平均效率。无序状态下不同数据规模时各排序算法的执行时间如图3所示。

图3 随机初始化不同数据规模时各种排序算法执行时间比较

因各种算法在有些情况下执行时间差异非常大，所以在时间比较过程中纵坐标轴采用了对数刻度。在随机初始化序列的状态下，当待排序的数据规模小于等于1万时，各排序算法的执行时间没有太大区别，执行时间都是在1秒钟之内。而当待排序的数据规模大于等于10万时，冒泡排序、直接插入排序、简单选择排序和二分插入排序的排序时间迅速增加，特别是当数据规模达到100 万时，他们的执行时间都达到了1,000 秒，冒泡排序甚至接近100,000 秒。数据规模达到1,000 万时，这几个排序算法的执行时间是让人难以接受的，也没有显示的意义，因此，在图3 中未加以显示。对于希尔排序、堆排序、二路归并排序和快速排序，当数据规模达到100万时，排序时间仍保持在1秒之内，当数据规模达到1,000 万时，四个排序算法中除希尔排序外其他排序算法排序时间保持在10秒之内。尤其是二路归并排序及快速排序，即使数据规模达到2,000万时，排序时间仍然保持在10秒之内。

因此，在随机初始化序列状态时，当数据规模小于等于1万时，排序算法对排序效率没有太大的影响。这时，原理简单，容易编程实现的冒泡排序和直接插入排序是可行的。当在数据规模到10万以上时，选择希尔排序、堆排序、二路归并排序和快速排序能显著地提高排序效率。其中，二路归并排序及快速排序的是排序效率最高的算法。

3.2 正序状态下不同数据规模各种排序算法的时间效率

在待排序数据为正序的情况下用不同数据规模的数据对排序算法进行性能测试，所得结果可以为在数据基本有序的情况下选择合适的排序算法的依据。正序状态下不同数据规模时的排序算法执行时间如图4所示。

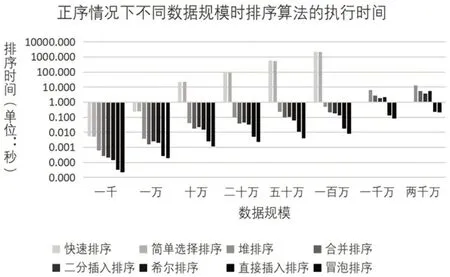
图4 正序初始化不同数据规模时各种排序算法执行时间比较

由图4可见，在正序状态下，当数据规模小于等于1 万时，同随机状态下一样，各种排序算法的执行时间没有太大的区别，都是在1 秒钟之内。当数据规模大于等于20万时，快速排序与简单选择排序所需时间大幅度上升，当数据规模达到100万时，这两个排序算法所需时间达到了1000 秒，当数据规模达到1000 万时，这两个排序算法的执行时间已让人难以接受，故图4中未进行展示。而其他六个算法始终保持着高效率，在数据规模达到2000 万时仍然能在10 秒内执行完毕，尤其是直接插入排序和冒泡排序（程序中判定了序列情况，设计了提前结束排序操作），可以在不到1 秒的时间完成。所以，当数据基本有序时，选择直接插入排序和冒泡排序是比较好的选择。

将图3 与图4 对比，可以发现，正序状况下同等数据规模时，大多数排序算法在所需时间相比于随机状态下所需时间更短，效率更高。且冒泡排序、直接插入排序和二分插入排序时间缩短明显，而在随机状态下效率最高的快速排序却在正序状况下耗时大幅度上升。这个现象将在后文通过对比较次数和移动次数的分析加以解释。

3.3 逆序状态下不同数据规模各种排序算法的时间效率

在待排序数据为逆序的情况下用不同数据规模的数据对排序算法进行性能测试，可为我们在待排序数据为逆序时选择排序算法提供参考。逆序状态下不同数据规模时的排序执行时间如图5所示。

通过将图5 与图3 对比可以发现，在在逆序状况下各排序算法的执行效率与在随机状态下基本相同，堆排序、希尔排序和二路归并排序仍然时排序效率最高的三种排序算法。

图5 逆序初始化不同数据规模时各种排序算法执行时间比较

所以，当数据基本上为逆序时，选择堆排序、希尔排序和二路归并排序是比较好的选择。

而逆序状况下的快速排序却同在正序状况下一致，对相同规模的数据进行排序时，排序时间远远高于在随机序列状况下排序时间。同样，这个现象将在后文通过对比较次数和移动次数的分析加以解释。

3.4 算法执行时间与比较次数、移动次数之间的关系

正确认识排序算法执行时间与算法运行过程中比较次数、移动次数之间的关系，能为选择合适的排序算法以及创建新的高效率的排序算法提供依据。综合分析随机状态下数据规模为100万时的排序执行时间与比较次数、移动次数及两个次数的总和的关系如图6所示。

图6 随机状态下100万数据规模时排序算计时间与比较次数、移动次数比较图

通过对图6 的分析，验证了排序算法的执行时间与所需的比较次数和移动次数总合存在正相关关系，而与单独的比较次数或移动次数没有直接关系。因此，当一个排序算法在排序过程中所需的比较次数和移动次数总合越小时，所需的排序时间就会越短，排序效率也就越高，这也是我们选择和设计排序算法的重要依据。

3.5 不同数据初始状况下排序时间与比较次数、移动次数总和的分析

通过排序算法执行时间与比较次数、移动次数之间的关系可知排序时间与比较次数、移动次数总和存在正相关关系。解释说明了不同初始状况下某些排序算法的执行效率会发生明显差异，便于认识不同排序算法在不同数据初始状况下的排序效率。故对100万数据规模时不同数据初始状况下排序时间与比较次数、移动次数总合进行分析，如图7所示。

图7 随机状态下100万数据规模时排序算法执行时间与比较次数、移动次数比较图

从图7可知，冒泡排序、直接插入排序和二分插入排序因为在对正序状态下的数据进行排序时执行的比较次数和移动次数总和非常低，所以在待排序数据为正序时，执行效率非常高。而希尔排序在对正序状态和逆序状态下的数据进行排序时执行的比较次数和移动次数总和非常高，所以在待排序数据为正序或逆序时，执行效率相对较低。

就同一个排序算法对不同初始状态的数据进行排序所需时间可以发现，冒泡排序、直接插入排序、二分插入排序只在待排序数据为正序时效率比较高，快速排序只在待排序数据为随机序列时效率较高，希尔排序、堆排序、二路归并排序在三种数据初始状况下效率都比较高，而简单选择排序在三种数据初始状况下效率都比较低。

4 结束语

本文对八种常见的排序算法进行了简略的理论介绍，重点设计了在不同数据规模、不同数据初始化状态下的各个排序算法的执行效率和比较、移动次数的比较分析，结论对理论知识的理解和掌握具有明显的促进作用。

不同的排序算法各有优劣，在选择排序算法时应综合考虑待排序数据的数据规模和数据分布情况，排序算法的执行效率和稳定性。基于实验结果，常用排序算法的适用情况总结如表2所示。

表2 常见排序算法的适用情况对比

陈国良院士指出，计算思维的第一功能是提出问题的解决方案和设计系统[8]，本文的实验设计，从排序算法理论为出发点，提出了针对性的如何评价排序算法这一问题，针对该问题，设计了包括不同初始化序列、不同数据规模的比较实验，对算法的执行时间，算法中涉及的数据元素比较次数、移动次数进行统计分析。这一过程有助于学生深入理解理论知识、增加实际动手能力，同时，可以促进学生主动学习，将数据结构中的算法灵活应用于实际解决问题的实践中。