基于逻辑回归的驾驶员信用评估研究*
张 华
(湖北民族大学智能科学与工程学院,湖北 恩施 445000)
0 引言
据公安部2022 年3 月发布的最新数据,全国机动车保有量为4.02 亿辆,机动车驾驶人4.87 亿人。2022年,我国道路交通事故万车死亡人数为1.80 人,同比有所下降,但整体比例仍然偏高,道路运输重大事故有所反弹,货车、农用车违规载人事故反复发生,客车重大事故和重大涉险事故频发。英美研究人员通过对大量事故数据的研究发现,与驾驶员相关的交通事故影响因素占93%[1],严新平对国内2001 年至2009 年死亡人数在3人/次以上的特大交通事故分析结果显示:90%以上的交通事故是由驾驶人主观因素导致的[2],因此对驾驶员进行全面评估显得尤为重要。
目前国内外已有较多驾驶人相关的研究成果,比如驾驶人行为识别[3]、驾驶人生理状态识别[4]、驾驶人行为画像[5]等,但对驾驶员信用评估研究较少,本文以交警历史数据为基础建立评价体系,通过IV 值筛选出重点特征,接着运用逻辑回归算法构建评估模型,最后对驾驶员进行信用评分,根据评分及时发现高风险人员以预防事故的发生。
1 数据采集
本研究所有数据来自“公安部交通安全综合服务管理平台”(以下简称六合一平台),该平台集机动车登记系统、驾驶证管理系统、违法处理系统、事故处理系统、交警队信息平台和剧毒品公路运输六大业务系统为一体。由于交警数据庞大,而且太久远的数据意义不大,因而设置了通过指定时间范围采集数据,另外,因为涉及个人隐私,在采集过程中将驾驶员的身份证信息做了脱敏处理。
根据交警数据的整体情况,将驾驶员的违章、事故、驾考、基本属性四个维度作为一级指标,一级指标下分9 个二级指标,分别是:违章程度(WZCD)、违章次数(WZCS)、违章频率(WZPL)、事故程度(SGCD)、事故频率(SGPL)、驾考全科目分数(KM)、驾驶人性别(XB)、年龄(NL)、驾龄(JL)。本文使用的数据集共4392 条数据,其中按照交警内部评审规则制定的失信驾驶员人数为962人,守信驾驶员人数为3430人。
2 变量选取
为提高模型预测的准确率,选择合适的指标十分关键,前述数据采集规定的字段只是初选变量,还需要进一步评估以确定最终特征变量。
2.1 IV值筛选
信息值(IV)是评价变量对目标影响程度的指标,即衡量变量的预测能力[6]。信用评分模型一般使用IV值筛选法筛选入模的特征变量,而IV 值的计算是基于证据权重(WOE),一种通过分组处理原始变量的编码形式[6]。WOE 值反映了某些变量的特征区分度,需要先对特征变量进行分箱处理,才能计算该变量的WOE值。分箱就是将一个连续型变量离散化,对其进行分组,然后统计分组好坏样本的个数,即驾驶员中失信人数和守信人数,计算出各自的占比,然后计算出当前分组中失信驾驶员比例和守信驾驶员比例的差异,得出当前特征变量的WOE 值,单个分箱的WOE 计算公式为:
IV 值的计算是以WOE 值为基础的,具体的计算公式为:
经过对数据的预处理之后,使用分箱函数对特征变量进行WOE 分箱,进而计算出特征变量的IV 值,如表1所示。

表1 特征变量IV值及操作
IV 值能较好地反映特征变量的预测能力,变量的IV值越高,表示该变量的预测能力越强。本文选择IV值在0.1 以上的变量,最后保留违章次数、违章程度、违章频率、驾考分数、驾龄五个变量。
2.2 相关性检测
特征变量的多重共线性会直接影响模型预测结果的精确性,也会影响特征变量对结果的解释性[7]。因此,使用IV 值对特征变量进行筛选之后,还要检测这些筛选出来的特征变量是否存在多重共线性,下面是五个变量的相关系数矩阵。
从表2可以看出违章程度和违章次数相关性系数超过了0.5,表示这两个特征的相关性很强,由于违章程度IV 值更高,保留它而删除违章次数,因此将违章程度、违章频率、驾考分数、驾龄四个特征作为最终输入。

表2 特征变量相关系数
3 模型构建
3.1 Logistic回归模型
逻辑回归模型用于数据分类,原理涉及线性回归模型中的线性回归方程,其表达式为:
线性回归是用于预测连续变量的,而逻辑回归是用于预测类别的,即预测离散变量的。通过Sigmoid函数,逻辑回归模型可以对线性回归的输出进行非线性转换,得到0 到1 之间的概率值。对于二分类问题而言,其预测为1的概率可用如下公式计算:
其中,y 为线性回归方程,当P>0.5 时说明当前数据属于1 类,即守信的驾驶员;当P<0.5 时说明当前数据属于0类,即失信的驾驶员。
3.2 Logistic回归模型参数估计
将采集的数据集划分为70%训练数据和30%测试数据,训练后模型参数如表3所示。
当P 值小于0.05 时,特征变量与目标变量有显著相关性,通过表3可以看出,输入模型四个特征变量的P 值都小于0.05,即通过IV 值筛选的四个特征变量都可以作为模型的输入。
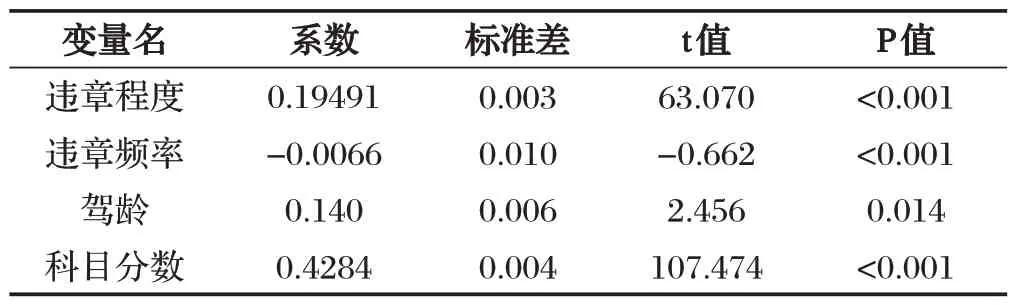
表3 模型参数
3.3 Logistic回归模型预测结果
接下来利用训练的Logistic 模型对30%测试集样本进行预测,使用分类评估器对Logistic 回归的预测结果进行评估,准确度为92.21%,说明模型能够较为准确的预测,如表4所示。

表4 分类结果评价指标
4 模型应用
Logisitc 回归输出的结果是驾驶员是否失信的概率,不够直观,因此还需要将预测的概率值转换为具体的分值,即将模型输出的失信样本概率和正常样本概率的比值通过线性转换得到最终的信用评分。
4.1 评分计算
根据逻辑回归原理,客户失信概率p可以如下表示:
其中,x为客户特征,θ为特征系数,式⑸整理得:
失信概率和正常概率比值称为比率odds,即:
设评分卡分数为:
其中,A、B是待求解数,B前取负号表示失信概率越高分数越低,信用也就越低。
假设比率为θ0时的基准分为P0,比率翻倍为2θ0时分数的变动值为PD0,带入公式⑼可得:
对公式⑽进行求解,可以得到A、B的值:
其中,P0、θ0、PD0都为已知常数,可以求出A、B的值,然后将A、B 的值带入公式9,即可得出信用分数的计算公式。
4.2 等级划分
传入评分卡公式及预测结果,即可计算出每个样本的信用评分,结果如图1所示。

图1 信用评分分布
从图1 可以看出,3198 人分数集中在60 分以上,1001人分数在30分以下,193人分数在50~70分之间,符合本文所用数据集的数据分布情况,因而可对驾驶员进行信用等级划分,分为四个信用等级:高风险、低风险、正常、良好,信用评分等级如表5所示。

表5 信用评分等级表
5 结束语
本文为解决驾驶员评估的问题,以某地区六合一平台历史数据为基础,在对数据进行预处理和构建信用评价指标的前提下,通过IV 值筛选变量并运用Logistic回归算法构建评估模型,最后计算用户的信用评分并划分风险等级。实验表明,该模型准确度达到92.21%,能较好识别出高风险驾驶员。下一步计划联合其他机器学习算法,进一步提高模型识别精度。

