基于量子粒子群优化SVM算法的水质预测研究

阎 凤

(上海城投水务（集团）有限公司自来水业务受理分公司，上海 200040)

0 引言

水质预测是水环境治理的一项基础工作，是资源环境承载能力监测预警的重要组成部分，建立准确的水质预测模型可以为管理部门水资源保护科学决策提供重要支持。水质预测模型通常利用流域属性数据或者各类时序数据，建立非线性关系模型或时序特征模型。传统的水质预测模型主要包括时间序列模型、灰色系统理论模型、回归分析模型以及神经网络模型等。雷勇等[1]采用线性回归模型实现在线水质监测系统的设计与实现。于慧等[2]采用灰色GM(1,1)模型对海河三岔口断面的溶解氧等多项指标年度变化趋势进行预测。周添一等[3]采用优化的非线性有源自回归模型（Nonlinear autoregressive with exogenous inputs,NARX）对时间序列溶解氧进行预测。时间序列模型过于强调时间因素在预测中的作用，忽视了其他水质影响因素和水质项之间的关系。Wang 等[4]利用长短期记忆网络（Long short-term memory networks,LSTM）模型预测城市污水的化学需氧量。王昱文等[5]采用复合神经网络对四项水质指标进行预测。石翠翠等[6]基于水质参数与溶解氧的复杂非线性关系，采用支持向量机方法研究水质预测模型。

支持向量机（Support Vector Machine,SVM）是一种基于统计学习理论的机器学习算法，以解决小样本量和非线性问题而著称，是研究人工智能、数据分析、人脸识别等领域的一个重要方法。SVM 虽然有许多优点，但是在处理大样本容量等分类问题时存在不足。当训练样本数为N时，SVM 的时间复杂度接近N2[7]。另外，SVM 对参数的选取具有高度依赖性，核函数和惩罚因子等参数的选取将直接影响SVM 的泛化性能与分类精度，因此，SVM 参数优化方法的研究对其发展和应用起着非常重要的意义[8]。

现有的SVM 参数优化方法主要有果蝇算法、遗传算法和粒子群优化算法等。宋娟等[9]提出了一种集成果蝇优化算法（Fruit Fly Optimization Algorithm,FOA）和SVM 的混合优化策略FOA-SVM 来提高天然气短期负荷预测的准确度。赵新等[10]提出了基于改进果蝇算法优化SVM的模拟电路故障诊断方法。Huang等[11]利用遗传算法（Genetic Algorithm,GA）对SVM 中的损失参数，核函数参数和损失函数epsilon 的值进行优化，提出了GA-SVM 模型来分析气候变化和人类活动对植被覆盖变化的定量贡献。Chen 等[12]提出了一种基于GA-SVM 的拉曼光谱技术，可以快速有效地筛选人乳头瘤病毒，并通过使用遗传算法优化SVM 模型中的惩罚因子和核函数参数来提高模型的准确性。粒子群优化（Particle Swarm Optimization,PSO）算法作为一种基于群体智能的随机搜索算法，其主要特点是收敛速度快、易于实现。康琛笠等[13]提出了一种基于粒子群优化支持向量机(PSO-SVM)的局部放电模式识别方法。Liu 等[14]利用PSO-SVM 模型来预测每日PM2.5 水平，通过算法对比表明了PSO-SVM 具有最高的准确性和效率。马钢等[15]提出一种基于PSOSVM 模型的油气管道内腐蚀速率预测方法。粒子群优化算法虽然原理简单、易于实现，但是它所设置的参数过多（例如惯性因子，学习因子等）以及缺少随机性，极易陷入局部最优，而量子粒子群优化（Quantum Particle Swarm Optimization,QPSO）算法取消了粒子的移动属性，粒子位置的更新跟该粒子之前的运动没有任何关系，所以它具有全局随机性，搜索速度快，计算精度高的特点[16]。本文提出一种基于量子粒子群优化的支持向量机（QPSO-SVM）算法，用于水质预测研究。

1 方法描述

1.1 支持向量机

支持向量机首先由Cortes 和Vapnik 在1995 年提出。它是一类按监督学习方式对数据进行二分类的算法。其基本思想是在样本空间中构造一个超平面作为决策线，将两类不同的样本彼此划分开。以下是SVM算法的推导过程。

首先，在一个二分类问题过程中，给定一个N个训练样本构成的集合S，S={(xi,yi),i=1,2,…,N}其分类超平面的表达式为：

其中，w为超平面的法向量；b为超平面的平移距离。

SVM 欲找到具有“最大间隔”的划分超平面，其目标函数表示为：

如果所有的训练样本都满足约束条件，则说明集合S是线性可分的。

为了增加SVM 分类器对误差的容错性，需要在目标函数中添加松弛变量ξi和惩罚因子C，此时目标函数表示为：

当面对非线性分类问题时，SVM 算法将输入数据映射到更高维的特征空间中来解决非线性分类问题。为了避免维数过高的问题，引入核函数k(xi,xj)，本文选用的是高斯径向基核函数：

其中，参数б影响着从样本空间到特征空间的映射。将目标函数引进广义拉格朗日乘子，此时，优化问题可以重新表示为：

其中，αi为拉格朗日系数，则最终优化的超平面表示为：

1.2 主成分分析

主成分分析是分析多个特征间相关性的一种多元统计方法。它的基本思想是通过少数几个主成分来揭示多个特征间的内部结构，即从原始数据多个特征中降维到少数几个特征，使它们尽可能的保留原始数据特征间的关系，且彼此间互不相关。主成分分析在人工智能、数据挖掘和图像识别等领域发挥了重要的作用。下面是主成分分析算法的简单推导过程。

假设样本点xi在新空间中超平面上的投影是WTxi，若所有样本点的投影能尽可能分开，则应该是投影后样本点的方差最大化。投影后样本点的协方差矩阵是，于是优化目标可写为：

其中，W=(w1,w2,...,wd)。

对公式⑺使用拉格朗日乘子法可得：

于是，只需对协方差矩阵XXT进行特征值分解，将求得的特征值排序：λ1≥λ2≥...≥λd，再取前d’个特征值对应的特征向量构成W*=(w1,w2,...,wd’)。

PCA算法的步骤如下。

步骤1设定初始数据集D={x1,x2,…,xm}和低维空间维数d’。

步骤2对所有样本进行中心化处理：xi←xi-

步骤3计算样本的协方差矩阵XXT，并对协方差矩阵XXT做特征值分解。

步骤4取最大的d’个特征值所对应的特征向量w1,w2,...,wd’。

1.3 量子粒子群优化（QPSO）算法

1.3.1 PSO算法

PSO 算法由Kennedy 和Eberhart 在1995 年提出，它是通过模拟鸟群觅食行为而发展起来的一种基于群智能的随机搜索算法。它的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。

粒子群优化算法的数学描述为：在一个n维搜索空间中，设粒子群规模为m，则第i个粒子当前的最优位置为：

整个粒子群当前的最优位置为：

粒子群中每个粒子的速度更新公式为：

其中，c1，c2为学习因子；w为惯性因子；rand1和rand2是均匀分布在[0,1]区间的随机数；vi(t)为第i个粒子的速度，xi(t)为第i个粒子的位置；t代表迭代次数。

粒子群中每个粒子的位置更新公式为：

1.3.2 QPSO算法

由于PSO 算法需要设定的参数(惯性因子w，学习因子c1，c2)太多，不利于找到待优化模型的最优参数，而且粒子位置变化缺少随机性，容易陷入局部最优。针对这些问题，本文提出一种性能更高的优化算法—量子粒子群优化算法。QPSO 算法取消了粒子的移动方向属性，增加了粒子变化位置的随机性。以下是QPSO算法的计算过程。

QPSO 算法引入的新名词mbest，它表示pbest 的平均值，即平均粒子历史最优位置，公式为：

其中，M为粒子群的大小。

粒子i当前的最优位置更新公式为：

其中，Φ为(0,1)间的均匀分布数值。

每个粒子位置更新公式为：

其中，μ为(0,1)间的均匀分布数值;α为创新参数，一般其值不大于1。取+和-的概率为0.5。

2 基于PCA和QPSO优化SVM参数

当一个数据集的特征属性过多时，会影响SVM 模型预测的准确度及计算速度，因此首先对数据集进行降维处理，利用PCA 算法将数据集降到低维再进行数据分析。其次，SVM 的分类效果对RBF 核函数б和惩罚因子C的选取有着极高的依赖性，因此本文通过QPSO 算法优化SVM 模型中的惩罚因子C和RBF 核函数б。最后将最优参数带入到SVM模型中进行分类预测。PCA 和QPSO 优化SVM 参数过程如图1 所示，具体步骤如下。

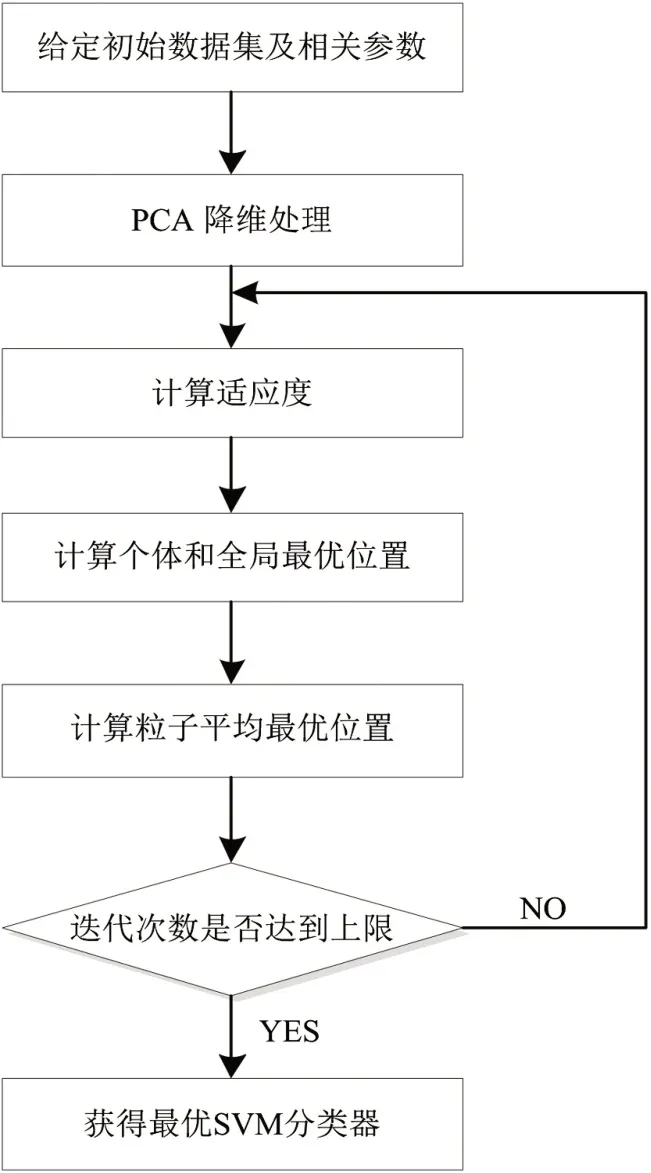
图1 PCA和QPSO优化SVM参数

步骤1给定初始数据集Q，确定QPSO 初始参数，如粒子群的数量，参数的取值范围，α值等。

步骤2利用PCA 算法将数据集Q 进行降维处理得到数据集Q’，如果数据集的数量级相差较大，需进行标准化处理。

步骤3设定适应度函数。本文设置的适应度函数为粒子在5-fold 交叉验证（Cross Validation,CV）下的分类精度。将数据集Q’作为QPSO 算法的输入，通过当前例子的位置向量，训练SVM 模型，并计算适应度值，更新每个粒子的最优值pbest 和全局最优值gbest。

步骤4计算粒子群中值最优位置mbest，更新每个粒子的新位置。

步骤5判断结束条件。当寻优达到最大迭代次数时，则寻优结束；否则转至步骤3，继续寻优。

步骤6将得到的粒子最优位置，即最优参数(C，б)赋给SVM，并进行分类预测。

3 仿真结果与分析

3.1 数据的收集和编码

本研究数据来源国家地表水水质自动监测实时数据发布系统，上海各区断面水质数据。分类的目标是预测未来断面水质类别。数据集包括九个属性。每一个属性都是国控水站水质评价指标。这些属性包括水温、pH、溶解氧、电导率、浊度、高锰酸钾盐指数、氨氮、总磷、总氮共九项检测指标。为便于表示，用A1～A9 代替，原始数据集如表1 所示。通过对数据集九个特征属性分析，利用PCA 算法对数据集降维，将降维后的数据集带入到QPSO-SVM 模型中进行预测。以上的所有编程环境均在Pycharm2019 中实现。为了更加直观地看出每个特征的分布情况，我们通过直方图进行展示，如图2所示。

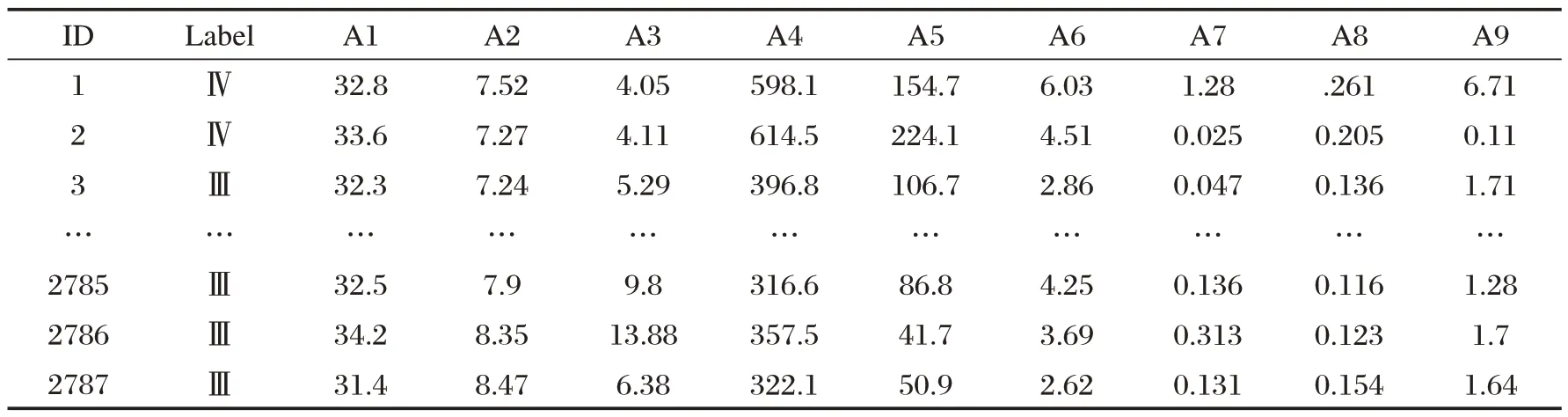
表1 原始数据集

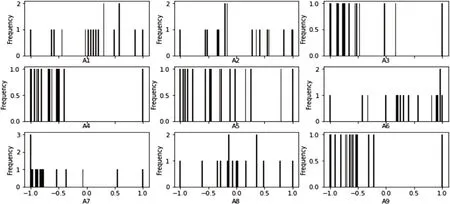
图2 数据集特征直方图

从图2 中可以看出，特征A1 至A9 的分布都比较分散，说明该九个特征对于模型的分类效果都有影响，分类效果明显。

3.2 PCA算法的数据降维

接下来，利用PCA 算法对表2 的数据进行降维处理。由于数据样本的属性值范围差距较大，首先需要对数据集进行StandardScaler 处理。在PCA 算法中，本文设置的参数为n_components=2。通过运算，得出PCA 降维后的数据如表2 所示，其中，X1，X2为主成分分析降维后的二个主成分元素。

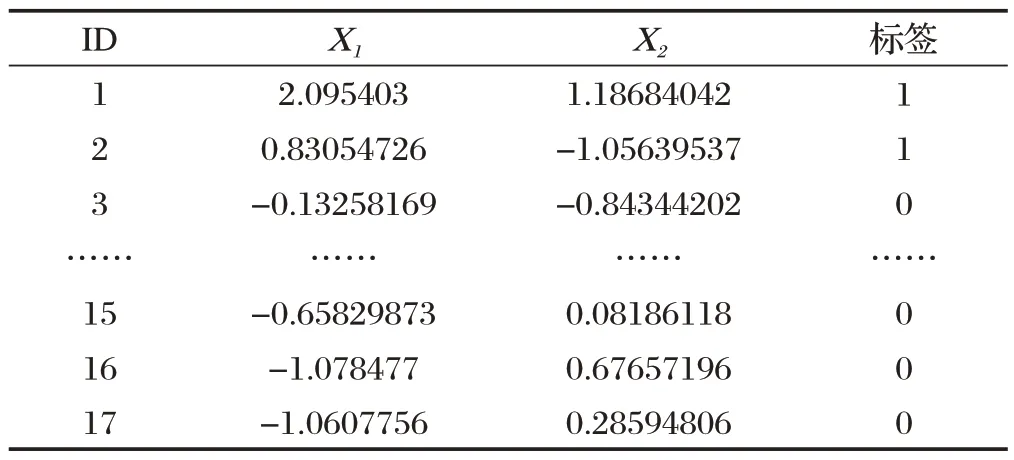
表2 PCA降维后数据

为了能够更加清楚、直观地观察数据经过PCA降维后的分布情况，下面对17组数据样本进行可视化处理。以X1为x 轴，X2为y 轴，建立二维直角坐标系，建立后的直角坐标系如图3 所示。（选取了17 个样本，从九维特征降维至二维特征可视化如：）

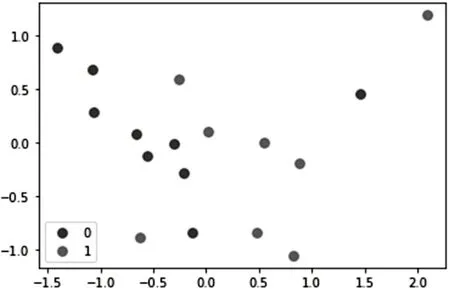
图3 PCA降维后的数据集分布情况

为了能够数据的可视化，通过PCA 算法将原始的九个属性特征降维至二个属性特征，从而减少了七个属性特征。为了验证该二维特征与原始九维特征的替代情况，通过关系热度图直观地显示出原始特征与PCA主成分之间的关系，如图4所示。

图4 主成分与各特征值之间的关系热度图

在图4 中，颜色由深至浅代表一个从-0.4～1.0 的数值，如果某个特征对应的数值是正值时，说明它和主成分之间是正相关的，如果为负值则相反。从图4中可以看出，X1对应的A2，A3 的相关系数极低，X2对应的A1，A5 的相关系数极低。这说明，经过PCA 算法降维后得到的X1，X2替代效果是较好的。

3.3 多分类QPSO-SVM模型的构建及参数设定

首先，将PCA 算法得到的二维数据集作为多分类SVM 模型的数据集，高斯RBF函数作为内核函数。然后，结合QPSO 算法并进行3-fold CV 的参数寻优，找出最优参数对（C，б）来运行多分类SVM 模型。在QPSO算法中，通过每一次迭代得出一个参数对（C，б），反复迭代到最大的迭代次数输出最优的参数对（C，б）。QPSO算法的具体参数设置如表3所示。

表3 QPSO算法参数设定

通过QPSO 算法参数值的设定计算出最优的参数对（C,б），然后将其作为多分类SVM 模型的参数设定值进行预测分析。

3.4 QPSO-SVM模型的求解

为了评估训练模型的性能，使用分类精度作为度量。QPSO-SVM 通过迭代得出的5-fold CV 下的分类精度过程如图5所示。

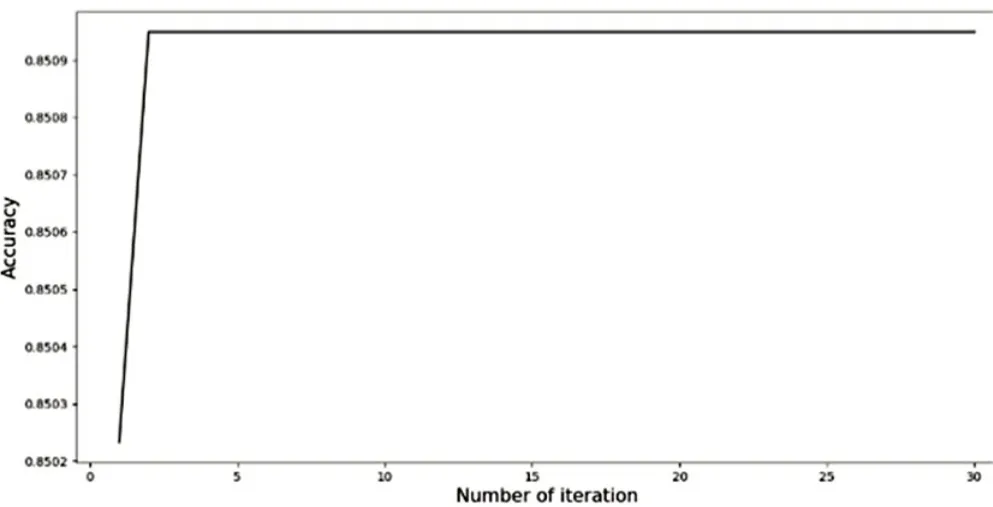
图5 QPSO-SVM参数寻优

通过QPSO-SVM 算法得出，当迭代次数到第2 次的时候，分类精度（即85.09%）达到最高，此时得出最优参数值C=3.91619，б=0.0001。将最优的参数带入多分类SVM 模型中，并用697 个测试集样本验证该模型的分类精度，得出预测精度为87.37%。

为了对比所提方法的优越性，本文将QPSO-SVM模型与PSO-SVM 和SVM模型进行对比，如表4所示。

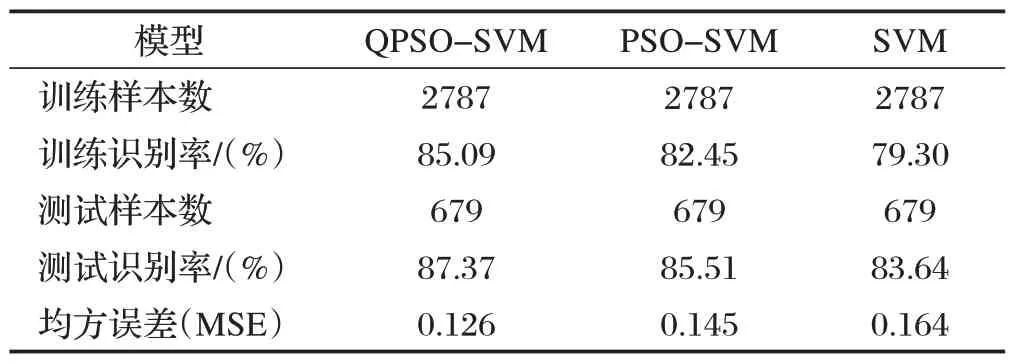
表4 模型的精度对比

从表4 可看出，QPSO-SVM 的训练识别率和测试识别率都高于PSO-SVM 和SVM 模型，QPSO-SVM模型训练样本的识别率达到了85.09%，测试样本的识别率达到了87.37%，均方误差也低于其他算法。综上可看出QPSO-SVM 模型有更好的分类精度，也说明了该模型的优越性。

4 结束语

本文研究基于支持向量机的水质预测模型。SVM 对于内部参数具有高度依赖性，针对SVM 参数寻优问题，本文提出了PCA-QPSO 算法优化SVM 参数对（核函数б、惩罚因子C）。首先通过PCA 算法对原始数据集进行降维处理，然后利用QPSO 算法优化SVM 中的惩罚因子C和核函数б，将得到的最优参数对带入到多分类SVM 模型中，用测试集来对模型进行测试。最后，本文以上海各区断面水质数据预测进行验证。结果表明，PCA-QPSO-SVM 模型的训练精度和测试精度均高于PSO-SVM 和SVM模型。