高切向流速高声强条件下梯度阻抗吸声超材料研究

巨泽港， 吴 飞， 赵 疆， 胡 嫚， 高鸣源， 郝耀东， 陈达亮

(1． 西南大学 工程技术学院， 重庆 400715； 2． 重庆大学 机械与运载工程学院， 重庆 400030；3. 中国汽车技术研究中心有限公司， 天津 300300)

高切向流速和高声强复杂条件下低频宽带噪声的吸收一直是业界与学术界关注的难题。例如航空涡扇发动机中空气流速可达0.5马赫数，背景噪声声压级(sound pressure level, SPL)高达160 dB[1-2]。声波与吸声结构相互作用机理复杂，伴随强烈的非线性效应，导致传统吸声结构效果不佳。传统的声衬[3]由微穿孔板和单层蜂窝状空腔组成，称为单自由度(single-degree-of-freedom, SDOF)声衬，可以在有限频带范围内实现吸声[4-5]，作用原理相当于四分之一波长谐振吸声器。为拓宽噪声的吸声带宽，将双层穿孔板与双层蜂窝腔连接形成双自由度(double-degree-of-freedom, DDOF)声衬[6-8]。DDOF声衬相比SDOF声衬吸声性能有显著的提升，逐渐成为应用最广泛的声衬结构[9]。然而，随着涡扇航空发动机的涵道比不断提升，声衬设计空间的缩小限制了传统SDOF和DDOF声衬的吸声效果。在此背景下，新型声衬的设计迫在眉睫，逐渐成为当前研究的热点。

“超材料”通常用于描述由人工亚波长结构的周期性或随机排列组成的人工复合材料[10]。随着超材料在声学领域的大规模应用，声学超材料的负折射率、负质量密度、负等效弹性模量等新特性被发掘[11]，其中结构型声学超材料以其稳定的吸声效果和尺寸优势在建筑、交通领域应用广泛[12]。Liang等[13]提出空间卷曲型吸声超材料，该结构具有低频吸声性能和亚波长尺寸参数。Jones等[14]设计了斜面声腔变高度声衬，由微穿孔板与变高度的斜面声腔组成，试验结果表明，所设计的结构在700～1 200 Hz范围内，最高传声损失可达到40 dB。2014年，Beck[15]设计了一种新型声衬结构，由四分之一波长体积的亥姆霍兹谐振腔周期性排列组成双共振声衬。试验结果表明，引入的双共振结构在500～1 000 Hz频带范围内具有良好的吸声性能。Tang等[16]在微穿孔蜂窝声衬中引入波纹结构，声衬具有超宽带低频吸声性能的同时，还具备优良的强度和刚度。Wu等[17]通过将微穿孔板与卷曲通道耦合，在常压垂直入射情况下，实现了355～470 Hz的低频亚波长高效吸声。Huang等[18]通过将微穿孔板与内插管结构串联，设计了一种双自由度低频宽带声衬，试验结果表明，该结构可以在800～3 000 Hz频带范围内强烈衰减声能，最高传声损失可达52 dB。综上，切向流和高声强环境下，具有低频宽带吸声性能和深亚波长结构的声衬设计仍然是一个挑战，而微穿孔结构和卷曲通道耦合的吸声超材料在静态垂直入射条件下拥有良好的低频宽带吸声性能，但在高速切向流场与高声强声场耦合环境中的吸声性能仍有待研究。

本文提出一种适用于不同切向流速和高声强条件下的吸声超材料。建立了梯度阻抗调控理论和有限元模型，并通过试验验证，探究其吸声机理与调控规律。结果表明，相比相同尺寸参数的DDOF声衬模型，所设计的结构在500～3 000 Hz的频率范围内吸声性能明显更优，具有广阔的应用前景。

1 梯度阻抗调控吸声理论解析方法

穿孔面板由于具有尺寸分布均匀，阻抗调节度高，对切向流状态影响小等特点，将作为本文梯度阻抗调控结构的主要吸声部件。梯度阻抗调控结构模型与表征参数如图1所示。图1(a)代表吸声超材料单体，结构与流场和声场的作用方式如图1(b)所示，利用梯度阻抗调控思想将不同阻抗单体进行周期性排列组成测试模型，其在流管试验台上的试验过程如图1(c)所示。对结构中任意参数的调整最终都将通过阻抗影响整体吸声性能，为在流动的管道中实现高效的宽频吸声，需根据管内流速、声压级和声音的传播模型对阻抗进行综合调控。

(c)图1 微穿孔板耦合梯度卷曲通道吸声超材料示意图Fig.1 Schematic diagram of micro-perforated plate coupled with gradient FP channels for acoustic metamaterial

1.1 穿孔板非线性吸声机理及阻抗表达

声衬的吸声机理主要有两种：① 当管道中无流动且入射声压级较低时，穿孔处的能量耗散主要由黏性机理主导；② 当管道中存在流动或入射声压级较高时，穿孔处会产生非线性效应，结构的吸声性能无法表现为简单的线性叠加，穿孔板的阻抗也展现出与静态条件完全不同的性质[19]。管道内不存在流动时，高声强引起的声学非线性表现为孔口的声阻分量随声压幅值的平方根成比例增加，声抗分量有所减少。当高声强条件下还存在切向流时，声阻分量将会进一步增加，孔中的流场存在完全不稳定的表现，Lee等[20]的模型通过在声阻中引入临界频率，简化了切向流和低声压级下的穿孔板阻抗方程。当把高声强产生的孔内粒子速度波动考虑在内时，Lee的半经验修正方程可以进一步表述为

Rn=a0(1+a1|f-f0|)(1+a2M)(1+a3d)×

(1+a4t0)/σ+u0/(σc0)

(1)

In=b0(1+b1d)(1+b2t0)(1+b3M)(1+b4f)/σ

(2)

式中：M代表流动马赫数；d代表穿孔直径；t0代表板厚；f代表入射频率；σ代表穿孔率；ai和bi代表回归系数，分别为a0=3.94×10-4，a1=7.84×10-3，a2=14.9，a3=296，a4=-127，b0=6.00×10-3，b1=194，b2=432，b3=-1.72，b4=-6.62×10-3，f0代表声阻的截止频率，可由式(3)表示。

(3)

式中，φi代表回归系数，分别为φ1=412，φ2=104，φ3=274。u0代表穿孔内部粒子运动速度，可由式(4)表示。

(4)

式中，Rl代表高声压级情况下的修正声阻，可由式(5)表示。

(5)

式中：ξ=2代表半经验常数；p0=2×10-5Pa代表参考声压。R0代表穿孔板在静态环境下的声阻，可由式(6)表示。

(6)

1.2 梯度阻抗通道吸声机理及阻抗表达

声波在卷曲通道中的传播方式如图1(b)所示，假设共有N个卷曲通道，利用式(7)和(8)可计算出每个通道顶部入口处的表面阻抗。

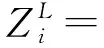
(7)

(8)

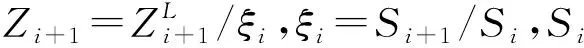
(9)

(10)

式中：αk=(2k+1)π/W0和βn=(2n+1)π/Li为计算常数；μ′=κ/ρ0Cv；κ和Cv分别为热导率和恒定体积比热；P0和γ表示空气压力和比热率；μ和ρ0代表空气运动黏度和密度。

将阻抗修正后的穿孔板和卷曲通道进行耦合，图1(a)单体结构阻抗可定义为

Zs=ZM+ZC1

(11)

式中：ZM代表穿孔板的阻抗；ZC1代表卷曲通道第一通道顶部阻抗。图1(c)中整体声衬结构由梯度阻抗单体并联而成，总阻抗可定义为

(12)

式中：Zs(n)代表第n个单体的阻抗；Nt代表单体总数。

2 梯度阻抗调控结构有限元模型

建立流管与声衬内部空气域耦合分析模型，如图2所示，引入吸声系数α对声衬的吸声性能进行评价。

图2 穿孔板梯度卷曲通道耦合有限元模型Fig.2 Finite element model of gradient impedance sound absorbing metamaterials

声衬和流管形成的区域可视为一个消声器[22]，由于声衬构成了测试段的壁面，相当于在流管试验台内部引入了一个软壁面，导致在垂直于声衬表面的方向产生法向波数。在远离声衬的入口和出口处，截止频率以下的高阶频率得到充分衰减，声波依然可以视为平面波，通过测量消声器入口处的入射声压Pi和反射声压Pr、出口处的透射声压Pt，利用公式(13)可得到消声器的声能量反射和透射系数αr和αt。

(13)

在有限元模拟和试验过程中，声波能量在管道中只存在入射、反射和透射三种情况，因此利用式(14)可计算出消声器的吸声系数。

α=1-αr-αt

(14)

根据以上分析在商用有限元软件COMSOL Multiphysics 5.6中对吸声超材料耗散声能的过程进行建模，如图2(b)所示。使用声-热黏性声学耦合物理场计算管道与结构中的声场和能量变化。

当声波在光滑管道中传播时，黏性和热损耗可忽略不计，因此利用压力声学频域模块计算管道中的声学特性。在该模块中，由于不考虑温度方程，声波状态由Helmholtz方程控制[23]，即

(15)

式中：p为入射声压；ω代表角频率。背景压力场接口中定义声压幅值为pPa(p=p0×10(SPL/20))，声速为343 m/s，声波沿着x轴负方向入射。完美匹配层(perfect match layer, PML)是一种可与相邻域的介质实现阻抗匹配的特殊区域。通过无反射地吸收所有入射波，PML能够在背景压力场末端构建出无反射边界条件。

当声波进入穿孔板和曲折声腔组成的复杂结构中时，结构中的黏性和热损耗不可忽略，因此声衬区域的声场状态使用热黏性声学频域进行计算。在该模块中，声压、温度和传播速度由Navier-Stokes方程、质量守恒方程和能量守恒方程进行计算[24]。

iωρ0ut=∇g[ptI+2η2I(∇ut+(∇ut)T)(∇gut)/3]

(16)

(17)

iω(ρ0CpT-T0α0pt)=-∇g(-K∇T)

(18)

式中：ut为速度场；T和T0代表温度场和背景温度；pt和p0分别代表t时刻的声压和背景压力；Cp代表恒压热容；K和I分别代表导热系数和单位矩阵。由于空气壁面与固体壁面存在较大的阻抗差异，吸声体的所有壁面均假设为硬壁面，利用有限元计算可得到吸声器入口和出口处的声压状态。

3 梯度阻抗吸声机理与调控规律

在切向流高声强环境中，声衬在流场和声场的共同作用下，吸声性能与在静态环境下相比差别很大，因此在不同子通道卷曲数n和声腔总数量Nt的情况下，对声衬单体的吸声性能展开研究，尺寸参数如表1所示，其中σ取0.084。

表1 穿孔梯度卷曲通道尺寸参数Tab.1 Perforated gradient curl channel size parameter 单位：mm

130 dB入射声压级下，声腔通道数目n=2时，切向流速Ui对吸声系数的影响如图3所示，随着Ui的增大，吸声系数峰值明显降低，Ui≥60 m/s时，吸声系数峰值甚至低于0.2，这是切向流和高声强共同作用的结果，作用机理剖面图如图4所示，60 m/s的切向流和130 dB的高声强引起穿孔和声腔中质点振速和空气流速增大，产生声涡旋和气流涡旋，导致声能转化为涡旋的动能，随着涡旋脱落到管道中，这部分声能最终转化为管道中流体的内能。涡旋脱落导致的非线性效应使整体穿孔板声阻增大，声阻抗匹配失衡，大量声波被声衬反射而非吸收，导致声腔共振频率向高频移动。

图3 切向流速对吸声性能的影响曲线Fig.3 Influence curve of grazing flow speed on sound absorption performance

图4 高切向流速高声强在结构中的作用图Fig.4 Diagram of the role of high grazing flow speed and high sound intensity in the structure

通道卷曲数n相等时，声腔数量Nt对吸声性能的影响如图5(a)所示。相同的入射条件(Ui=0)和尺寸参数(n=2)下，Nt的大小造成声衬整体阻抗的变化，并进一步影响了吸声系数峰值和吸声带宽。声腔越多吸声系数峰值越高，吸声带宽也越大，因此在设计复杂工况下的吸声超材料时，合理选择声腔数目也是进行阻抗调控的有效途径。

(a) 相同结构的不同数目对吸声系数的影响

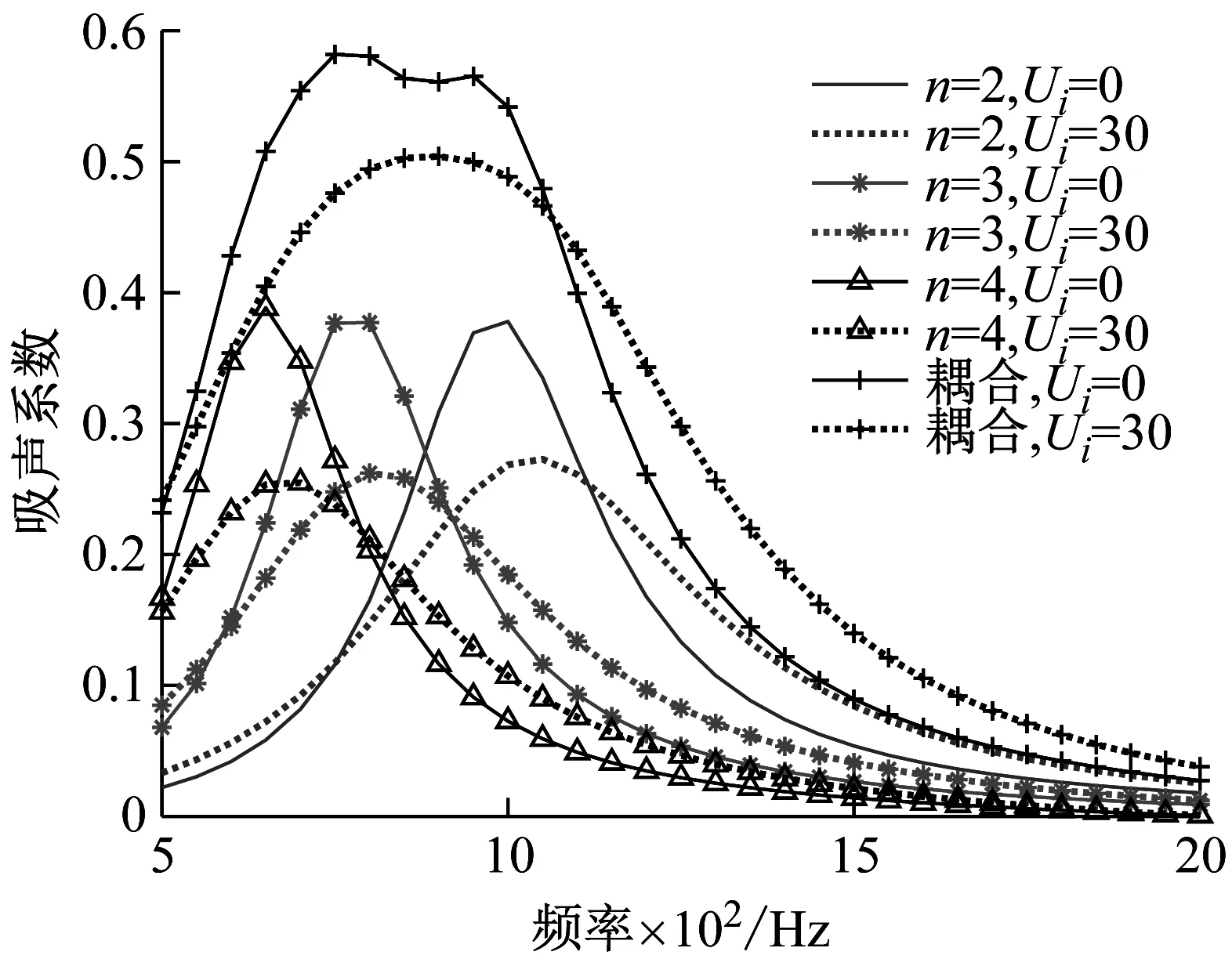
(b) 低切向流速下不同阻抗结构的吸声性能

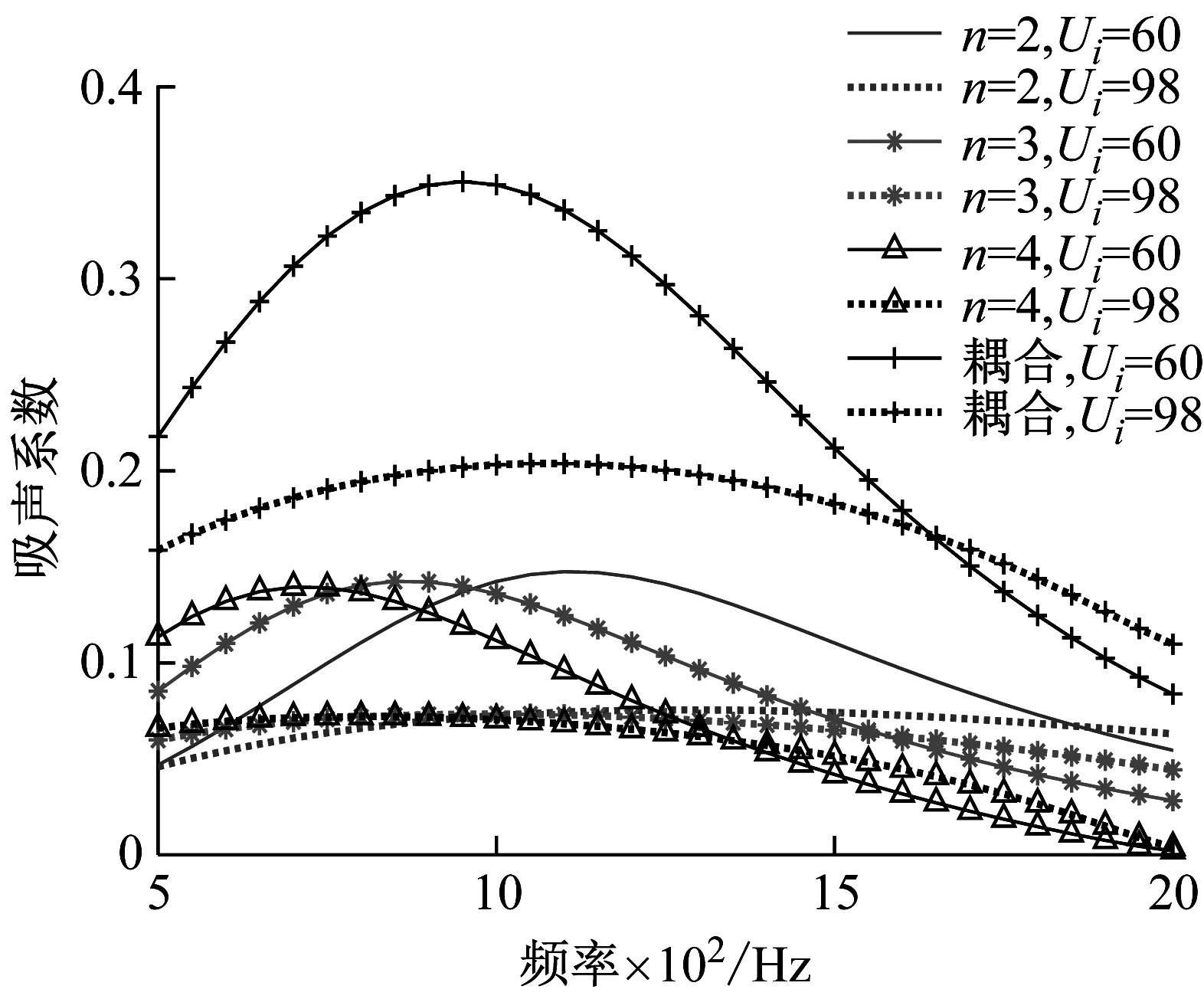
(c) 高切向流速下不同阻抗结构的吸声性能

(d) 不同阻抗结构耦合前后的整体阻抗变化图5 多阻抗耦合对吸声性能的影响Fig.5 Effect of multiple impedance coupling on sound absorption performance

通道卷曲数n不同时，吸声性能的变化如图5(b)和(c)所示。相同流速下，吸声系数峰值对应的频率随着n的变大逐渐降低，与静态垂直入射条件下的变化趋势一致。将三种梯度阻抗声腔结构耦合后，吸声性能显著提升，四种切向流速下的吸声峰值和带宽优于单一阻抗声腔的吸声性能，图5(d)为Ui=98 m/s时单声腔和多声腔耦合后的阻抗变化，单声腔情况下无法实现阻抗匹配，n=4时声阻和声抗的变化皆超过20。经过三种梯度阻抗的耦合，声抗在目标频段内维持在0附近波动，声阻也降到了四种情况中的最低水平，实现了梯度阻抗的宽带调控。

4 宽带设计与试验验证

为验证梯度阻抗耦合理论的准确性和结构优势，将具有相同穿孔板与声腔厚度参数的DDOF声衬和梯度阻抗声衬进行对比试验，尺寸参数如表1所示，其中DDOF声衬σ取0.042，梯度阻抗声衬σ取0.05。试验装置为上海交通大学振动冲击噪声研究所的风机流管测试平台装置，如图6(a)所示，该装置总长约8 m，为70 mm×100 mm矩形截面，由上下游声源段、气源段、样件安装段和上下游消声器段组成。在实际测试时，采用DSPPA MX2000功率放大器控制上游声源2个BMS 4599 ND扬声器产生最高135 dB声强，未安装扬声器的部位采用虚拟号筒进行密封。由离心风机产生的高速气流经过消声器段和流速测量段随声波共同作用于声衬表面。由11个Brüel&Kjær 4944-A传感器组成的阵列安装在管道下壁面以提取声衬表面阻抗。在声衬安装段的上游和下游额外安装4个传感器测量消声器的入射、反射和透射声压以计算吸声系数。传感器测量的声压数据利用BBM MKII数据采集系统进行处理。上下游消声段采用微穿孔变腔深结构，用于降低管道出入口的声反射现象以提高管道内部的声场品质。图6(b)为梯度阻抗声衬样件，图6(c)为DDOF声衬样件，穿孔板尺寸参数如表1所示。梯度阻抗样件声腔的等效吸声长度从1 mm至91 mm变化，迭代参数为5 mm，经过梯度阻抗调控形成图1(c)中的Lunit1，为满足声衬在流管试验台上的安装尺寸需求，加入Lunit2和Lunit3，其中Lunit2与Lunit1完全相同，Lunit3由Lunit1中前13个声腔组成，声腔总体厚度H为46 mm，试验入射声压级为130 dB，分别在0、30 m/s、60 m/s和98 m/s的切向流速下测试样件在500～3 000 Hz范围内的吸声系数和阻抗的变化。

(c)图6 试验装置和样件实物图Fig.6 Physical drawing of the test device and sample parts

记A1为梯度阻抗调控模型，A2为DDOF声衬模型。A1和A2理论预测声阻抗与测试声阻抗在不同切向流速下的分布情况展示在图7(a)～(d)中。当切向流速Ui=0时，A1的声阻曲线集中在1附近波动，声抗曲线在-1～2之间变化。相反，A2声阻和声抗曲线的波动范围均超过15，尤其在2 000～2 500 Hz之间变化显著，说明当不存在切向流时，A1的阻抗性能优于A2。随着流速的升高，两种模型的声阻抗均发生明显变化，A1的声阻曲线逐渐升高，声抗曲线逐渐降低，当Ui= 98 m/s时，声阻曲线整体大于1。相同条件下，A2的声阻曲线最高为18.4，声抗曲线最低为-8.1，难以实现阻抗匹配。

(a) Ui=0时的声阻抗

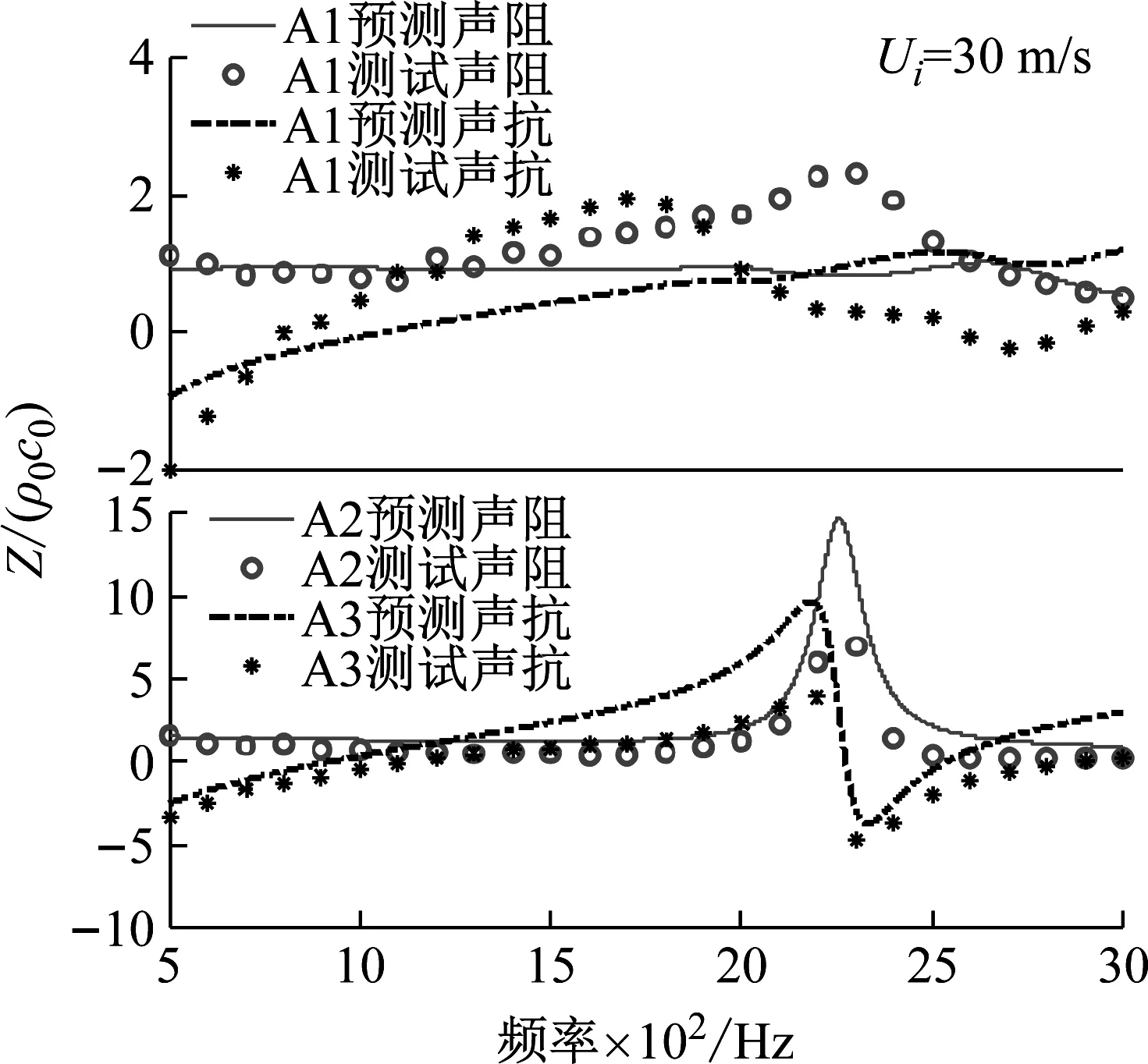
(b) Ui=30 m/s时的声阻抗

(c) Ui=60 m/s时的声阻抗

(d) Ui=98 m/s时的声阻抗图7 预测与试验声阻抗对比图Fig.7 Comparison of predicted and experimental acoustic impedance

更进一步，A1和A2理论预测吸声系数与测试吸声系数在不同切向流速下的分布情况如图8(a)～(d)所示。当切向流速Ui=0时，A1和A2模型在500～3 000 Hz范围内测试吸声系数平均值分别为0.8和0.67，A2模型在2 000～2 500 Hz范围内吸声系数降至0.4以下，而A1模型的吸声系数曲线仅出现小幅度下降，说明在无流条件下A1模型的宽带吸声性能优于A2模型。随着切向流速的升高，两种模型的吸声系数都出现一定程度下降，当Ui=30 m/s、60 m/s和98 m/s时，A1模型的测试吸声系数平均值分别为0.81、0.80和0.68，A2模型仅为0.72、0.75和0.65，在2 000～2 500 Hz范围内，A1模型吸声系数均高于A2模型，证明多声腔耦合的梯度阻抗调控法可有效拓宽吸声带宽，提升吸声系数峰值。在98 m/s的切向流下，A1和A2模型测试结果和理论预测结果出现较大偏差，这是由于高速切向流引起的强烈非线性效应导致穿孔板声阻显著升高，声阻抗匹配失衡造成了吸声系数快速降低，非线性效应的增强同时导致微孔内部声涡脱落现象明显，准稳态阻抗模型的误差增大。

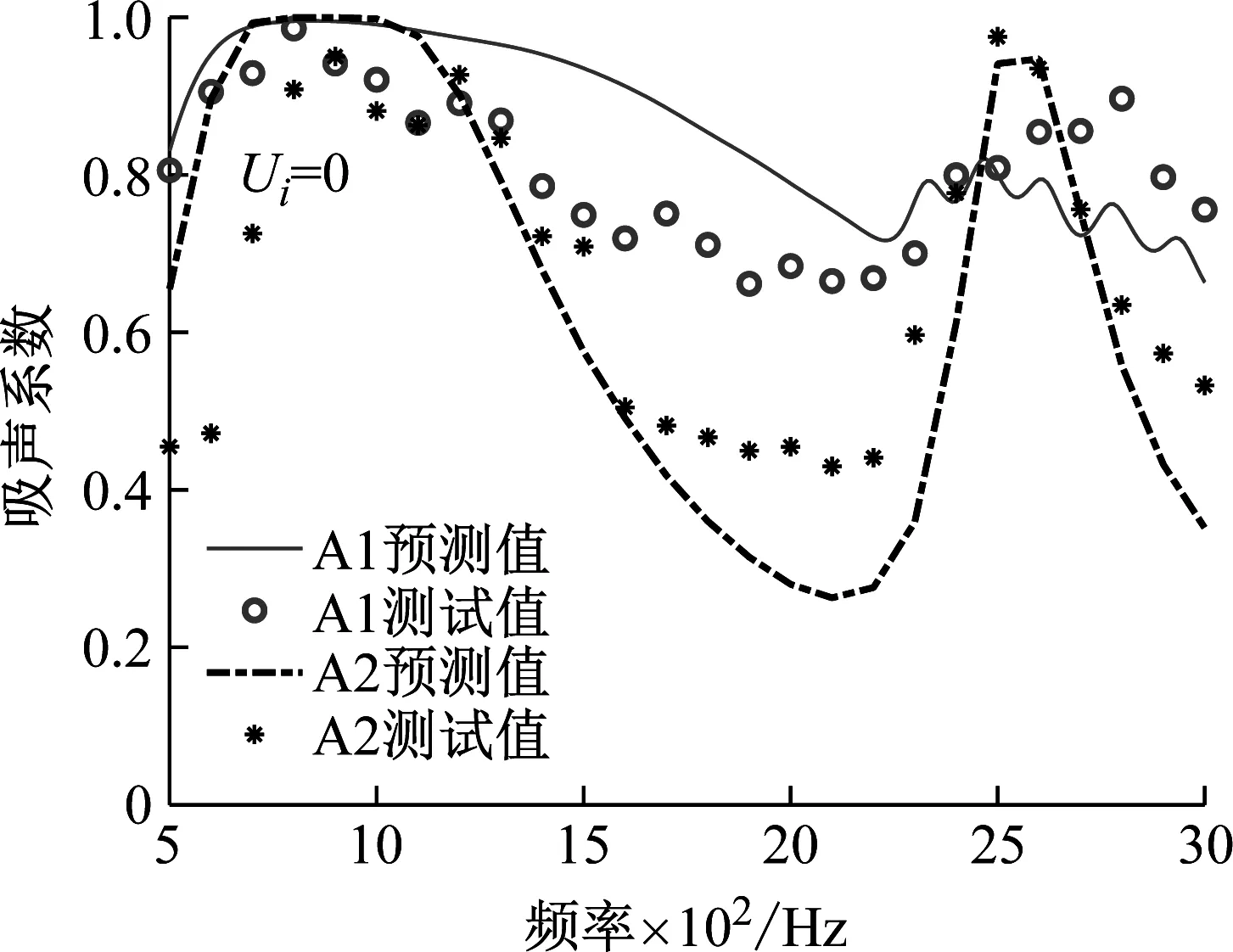
(a) Ui=0 m/s时吸声系数对比图

(b) Ui=30 m/s时吸声系数对比图

(c) Ui=60 m/s时吸声系数对比图

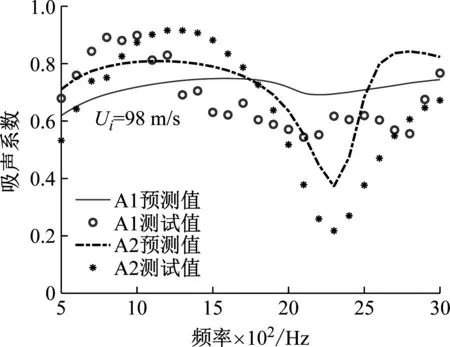
(d) Ui=98 m/s时吸声系数对比图图8 预测与试验吸声系数对比图Fig.8 Comparison of predicted and tested sound absorption coefficients

5 结 论

高切向流速和高声强耦合环境中，由于吸声机理和调控机制复杂，低频宽带噪声的吸收极具挑战性。本文通过将穿孔板与梯度阻抗卷曲声腔耦合的方式，设计出一种适应高切向流速和高声强的宽带吸声超材料。研究了该模型在130 dB入射声压级和0、30 m/s、60 m/s、98 m/s切向流共同作用下的吸声性能，建立了复杂边界条件下声衬的理论模型和数值模型，经过试验分析，梯度阻抗吸声超材料可以有效解决DDOF声衬吸声带宽窄的问题，四种流速下吸声系数峰值和带宽都优于同尺寸的DDOF声衬，样件厚度仅50 mm，小于500 Hz对应波长的3/40，具有良好的深亚波长特性。综上所述，本文设计的梯度阻抗吸声超材料因具有良好的低频宽带吸声性能，在高切向流速高声强降噪领域具有广泛的应用前景。