基于瞬时角速度信号窄带解调的太阳轮故障检测
尹兴超, 郭 瑜, 李震焘, 华健翔
(昆明理工大学 机电工程学院, 昆明 650500)
行星齿轮传动具有传动比大、结构紧凑等优点被广泛运用于工业机器人关节、直升机等[1]。目前对行星齿轮传动部件的故障检测主要基于对振动信号的分析。但固定安装的振动传感器拾取行星齿轮传动的信号时会受到时变传递路径的影响[2]不易直接分析;其次在工业应用中行星齿轮减速器常用于低转速工况,而加速度传感器的在低速工况中不易获得较好的检测效果。因此,研究能克服时变传递路径并能适合低速工况的行星齿轮减速器故障检测方法有重要意义。
目前能有效消除时变传递路径影响的方法为加窗振动分离[3],其原理为用一窗函数对行星齿轮减速器振动信号在行星齿轮啮合点距离振动传感器最近的固定位置(传递路径最短,信噪比高)进行加窗截取,当齿圈齿数与感兴趣齿轮齿数互质(最大公因数为1)时每次从振动传递路径最短的位置可以截取到齿轮(行星轮或太阳轮)按一定周期重复出现的啮合齿对应振动信号,再通过对各截取信号按齿序进行顺序拼接,可合成一消除了时变传递路径的人造齿轮信号,对该信号可用同步平均、窄带解调等常规齿轮故障检测方法进行故障检测[4]。值得注意的是,该方法用于太阳轮故障检测时仅当齿圈齿数与太阳轮齿轮齿数互质有效,此时,太阳轮的每个齿都会交替出现在振动信号传递路径最短的位置,可对太阳轮啮合信号进行完整截取。但若齿圈与太阳轮齿数不满足互质时,则该方法无法截取到太阳轮的所有齿,不能构造出完整的人造太阳轮啮合信号[5]。另一方面,最初被提出并用于转轴扭振分析和柴油发动机故障检测的瞬时角速度(instantaneous angular speed,IAS)具有噪声干扰少、直接与转子动力学特性关联等优势[6],近年在故障诊断领域受到关注,且在行星齿轮箱中IAS信号具有不受时变传递路径的影响、能够在低速工况中进行检测的优点。
本文使用IAS信号对太阳轮进行故障检测并结合角域同步平均、窄带解调等技术提出一种使用IAS信号对太阳轮故障检测的方法。首先通过高速计数器记录旋转编码器角度,同时使用T法[7-8]对相邻编码脉冲之间的时间间隔进行采集,以此计算IAS信号;角域同步平均用于IAS信号可实现准确提取与参考轴转速同步的分量,而对噪声及其它非同步分量进行抑制,提高信噪比[9];最后通过窄带解调[10-11]分别提取幅值和相位解调波形实现对太阳轮轮齿故障的检测。基于窄带解调的齿轮故障检测通常需通过观察幅值和相位解调波形在相同角度位置处出现的周期性峰值和相位突变,但在实际运用研究中发现行星传动IAS信号窄带解调获得的幅值与相位解调波形通常较为复杂,存在多个类似相位发生较大变化位置,直接观察难以对故障引起的相位突变进行准确判断,不利于在工程实际应用,针对这一问题研究中提出一种基于相位解调函数相位变化率的特征增强方法,实现对太阳轮齿根裂纹故障引起的相位突变的判断。
通过对无故障与有太阳轮故障的行星齿轮减速器的实验研究,证明使用本文所提方法可有效实现对太阳轮齿根裂纹故障的检测。
1 方法原理
1.1 光栅式旋转编码器简介
光栅式旋转编码器是一种用于测量旋转角度位置的装置,其原理结构如图1所示,由光栅编码盘和A、B、Z三个相位的光源及其对应的感光元器件组成,光源与感光元器件放置于编码盘的两侧,编码盘外圈刻有M个光栅用于生成A、B相的正交编码信号,在编码盘的内圈零位处刻有一个光栅用于产生零位信号即Z相,当编码盘旋转,其光栅经过光源时感光元器件便会接收到透过光栅的光学信号并将其转化为电信号以TTL的方式输出,光栅编码器A、B、Z三个相位波形如图2所示,因为A、B相信号为正交编码信号即在制造时严格保证这两信号的相位差为90°,在实际应用中为获得更高的旋转精度可进行倍频处理,令q为倍频数,在增量编码信号中当高速计数器只对其中一相的上升沿或下降沿进行计数时q=1、只对其中一相的上升沿与下降沿都进行计数时q=2、对两相的上升沿或下降沿其中一个进行计数时q=2、当对两相的上下沿进行计数时q=4。

图1 光栅编码器结构原理图Fig.1 Structure diagram of grating encoder

图2 A、B、Z相位波形示意图Fig.2 Schematic diagram of A, B and Z phase waveforms
1.2 IAS信号的测量与估计
不同于常规从齿轮箱轴承座处拾取的振动信号,IAS信号通过对旋转编码器输出的角度信号计算获得,其对应扭转振动,包含有丰富的转子状态信息。由于旋转编码器安装在转轴上,啮合点到传感器的路径长度不变,因此IAS信号在行星传动中不存在时变传递路径问题。当齿轮发生剥落、齿根裂纹等故障,故障齿啮合时啮合刚度较无故障状态将发生突变,由此引起对应IAS的规律性波动,因此IAS信号中包含有丰富的齿轮故障信息,据此可进行齿轮的故障检测。
设编码盘外圈上刻有M个光栅,使用高速计数器获取的第i个(i=1,2,3,…)编码器角度为φi,同时使用T法对相邻编码脉冲之间的时间间隔Δti进行采集,利用向前差分法可得[12]
(1)
式中:v(φi)为在编码器角度φi处的IAS信号;Δti为连续两编码脉冲之间的时间间隔;Δφi为编码盘相邻光栅间隔角度。忽略编码器制造误差,则Δφi=Δφ为常数,可表示为
(2)
式中:M为编码器线数;q为倍频数。本文中高速计数器只对A相的上升沿或下降沿进行计数,故q取2。
按设定转速运行的齿轮箱,受齿轮啮合刚度、齿轮故障和载荷波动的影响,其转轴瞬时转速并不保持恒定,去除其均值后IAS波动信号vc(φi)可表示为
vc(φi)=v(φi)-mean(v(φi))
(3)
式中,mean()为计算均值。
1.3 角域同步平均技术
角域同步平均可有效提取与选定参考轴转速同步的信号分量,同时抑制噪声和其它非同步干扰,广泛用于提高齿轮信号的信噪比。其算法可表示为[13]
(4)
式中:vcr(φi)为角域同步平均之后得到的IAS转速波动信号;p为平均段数;Tg为被检测齿轮信号的周期。
1.4 窄带解调技术
窄带解调包括幅值解调与相位解调[14]。为排除其它谐波的干扰,在解调前需选定解调频带,即阶比谱中某边带最丰富的啮合谐波为中心的频带,并进行带通滤波。对滤波后的信号vm进行Hilbert变换,对应的解析信号为
cm(φi)=vm(φi)+jH[vm(φi)]
(5)
式中,H[·]为Hilbert变换。对应的幅值解调函数为
am(φi)=|cm(φi)|/Am-E[|cm(φi)|]
(6)
式中:Am为n阶啮合谐波幅值;|·|为取绝对值;E[·]为取数学期望即平均。解析信号的相位解调函数为
bm(φi)=arg[cm(φi)]-(2πOmφi+φm)
(7)
式中,arg[cm(φi)]为cm(φi)的相位函数。
2 太阳轮故障检测
基于以上理论本文提出了基于IAS信号窄带解调的太阳轮故障检测方法,其实现如图3所示。

图3 基于窄带解调的太阳轮故障检测Fig.3 Sun wheel fault detection principle based on narrow- band demodulation
具体步骤包括:
步骤1使用高速计数器对编码器角度脉冲进行记录,并使用T法对相邻编码脉冲的时间间隔进行采集,从高速计数器中得到角度φi,由式(1)、式(2)和式(3)使用向前差分法得到IAS信号v(φi)并去除其直流分量得到其交流分量vc(φi);

步骤3设计带通滤波器对信号vcr(φi)滤波,根据文献[15],滤波器的通频带宽W最大取啮合阶比即W≤Om;滤波器的中心阶比为啮合阶比的谐波,假设选取第n阶谐波进行带通滤波,滤波器带通范围为
(8)
式中:Om为太阳轮啮合阶比;W为滤波器的带宽。
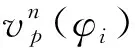
(9)
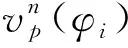
步骤5由式(5)对信号vp(φi)进行Hilbert变换得到解析信号cm(φi),再利用式(6)、式(7)得到幅值解调函数am(φi)与相位解调函数bm(φi)。
步骤6当齿轮存在故障时,其相位解调函数存在突变且突变发生频率与齿轮故障频率一致,同时在突变位置幅值解调函数在相位突变出现位置(相同旋转角度)会出现负峰值[16]。由于在实际运用中幅值与相位解调波形较为复杂,存在较多类似突变的位置,使得在实际应用中对齿轮故障引起的相位突变进行判断造成困难,针对这一问题,研究中提出用相位解调函数的相位变化率来增强对相位解调函数突变的判断。相位解调函数的相位变化率定义为
(10)
式中:PCR(φi)为相位解调函数的相位变化率;arg[cm(φi)]为cm(φi)的相位函数;cm(φi) 为Hilbert变换后的解析信号;Om为太阳轮啮合阶比。
3 实验研究
3.1 实验说明
研究中在行星齿轮传动试验台开展了实验研究。实验中对IAS信号与振动信号进行了采集并进行分析、对太阳轮齿根裂纹故障与正常的行星齿轮减速器进行实验,并使用本文所提方法进行太阳轮齿根裂纹故障检测。
行星齿轮传动试验台如图4所示,由伺服电机、行星齿轮减速器、光栅编码器、磁粉制动器等组成。

图4 行星齿轮传动试验台Fig.4 Test rig of the planetary gearbox transmission
行星齿轮减速器的齿数、变位系数如表1所示。实验时先对无故障的行星齿轮减速器进行IAS信号采集,之后使用电火花加工在太阳轮齿根处加工一条长3 mm宽0.3 mm的裂纹模拟故障裂纹,加工后的太阳轮如图5所示。实验时使用ReSatron公司的2 500线光栅编码器,输出方式为TTL信号,高速计数器对编码器信号采集(p=2),光栅编码器安装于行星齿轮减速器的输出端。对于振动信号的采集,使用的采集卡为 NIUSB9234,采样频率为 51.2 kHz;加速度传感器的型号为 DH112,加速度传感器安装于行星齿轮减速器壳体靠近齿圈处。实验时伺服电机转速设置为150 r/min,所用行星齿轮减速器传动比为5,输出端转速约为30 r/min。

图5 太阳轮齿根裂纹故障Fig.5 Sun gear with tooth root crack

表1 行星齿轮箱参数Tab.1 Parameters of planetary gearbox
实验中所使用的行星齿轮减速器太阳轮齿数为21、齿圈齿数为84,最大公因子为21,故太阳轮齿数与齿圈齿数不互质。根据文献[10]可得到太阳轮重复啮合的最小圈数ns,g为
(11)
式中:LCM()表示求最小公倍数;Ns为太阳轮齿数;Nr为齿圈齿数。根据式(11)计算得到ns,g=1,当振动传递路径最短时太阳轮参与啮合的齿不发生交替,使用加窗振动分离无法构建完整的人造太阳轮啮合信号来消除时变传递路径的影响。故振动加窗分离方法不适用于检测本次实验所用的行星齿轮减速器。
研究中以光栅编码器安装的输出轴(或行星架)为参考轴,根据行星齿轮传动理论[17]和表1中行星齿轮箱参数计算出各理论特征阶比如表2所示。

表2 行星齿轮箱特征阶比Tab.2 Characteristics order of planetary gearbox
3.2 实验数据分析
对太阳轮正常的行星齿轮减速器进行实验并计算得到IAS信号,其时域波形与阶比谱如图6(a)、6(b)所示。对存在人造齿根裂纹故障的太阳轮进行实验并计算得到IAS信号,为研究对比,同时采集振动信号,其IAS信号时域与频谱如图6(c)、6(d)所示,振动信号的时域信号与波形如图6(e)、6(f)所示。图6(b)、6(d)为IAS信号阶比谱,在IAS信号阶比谱中可以观察到行星架旋转阶比(1×)、太阳轮故障阶比(4×)、太阳轮旋转阶比(5×)、啮合阶比(84×)等。而振动信号的太阳轮故障阶比(4×)受时变传递路径的影响,阶比谱中无法观测到,由于受转速对振幅的影响与振动信号测量系统的限制,处于低频的行星架旋转阶比(1×)无法观测到,只能观测到输入轴旋转阶比(5×)及其倍频和齿轮啮合阶比(84×)。对比IAS信号与振动信号的阶比谱可以看出在低速工况下IAS可以采集到更加丰富的信息,且不受时变传递路径的影响。在太阳轮正常与故障IAS信号的阶比谱中都存在(4×),其原因是太阳轮故障阶比(4×)与行星架旋转阶比(1×)的4倍频(4×)、行星轮相对旋转阶比(4×)相重合,无法直接从阶比谱中对太阳轮故障进行判断,需要进一步对太阳轮故障特征进行提取。

(a) 太阳轮正常时IAS信号

(b) 太阳轮正常时IAS信号阶比谱

(c) 太阳轮故障IAS信号
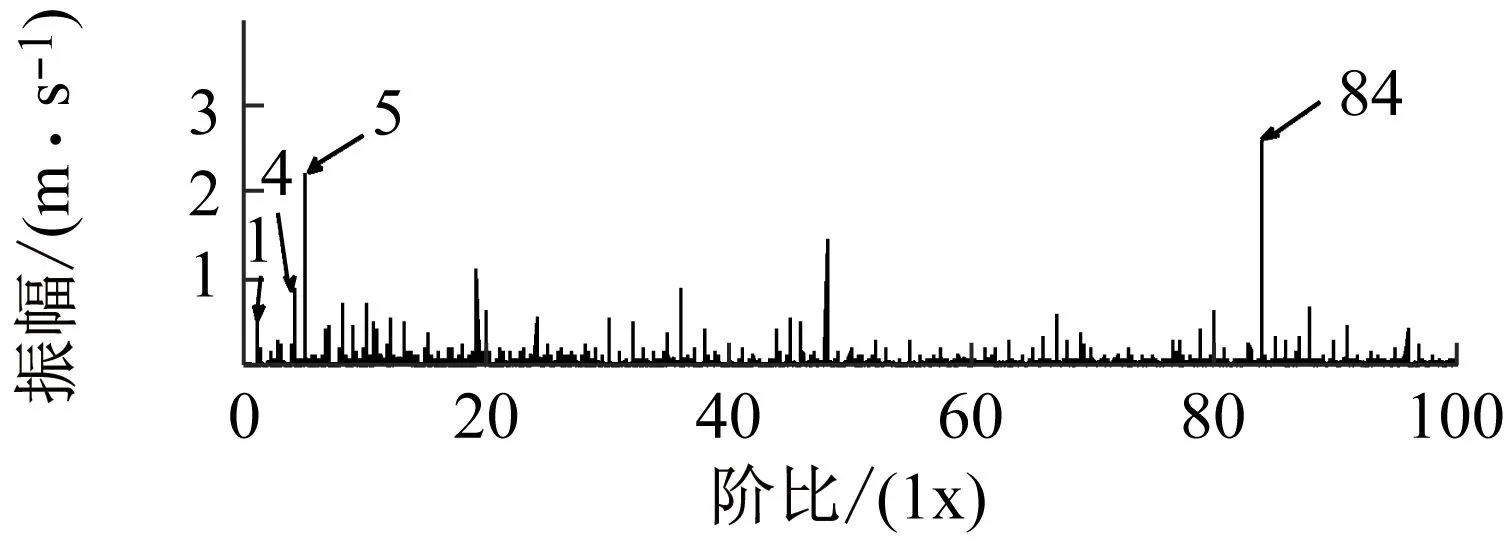
(d) 太阳轮故障IAS信号阶比谱
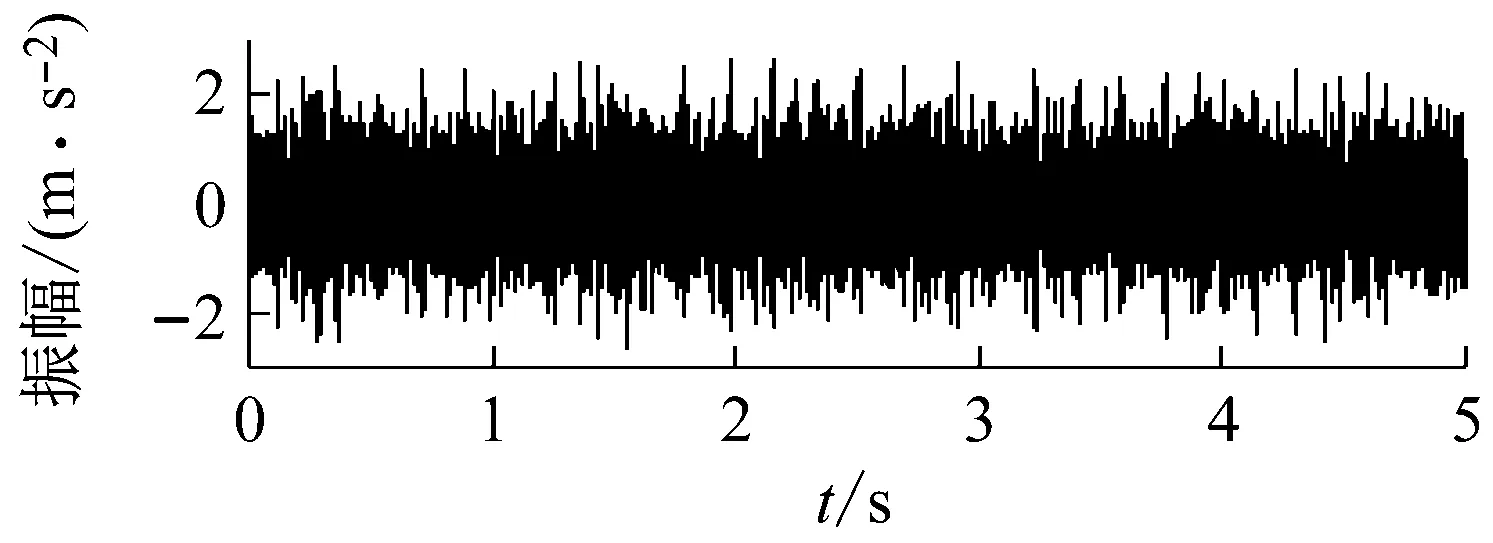
(e) 太阳轮故障振动信号
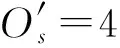
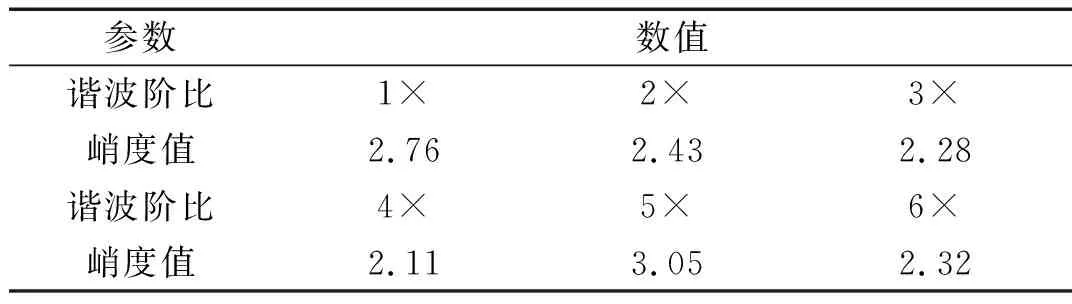
表3 峭度值Tab.3 Kurtosis value

图7 RSA后得到的角域IAS信号波形Fig.7 Angle domain waveform after RSA
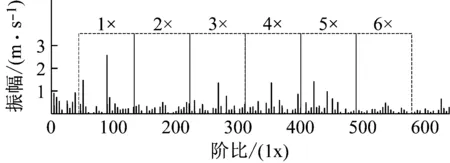
图8 前6阶谐波带通滤波范围Fig.8 First 6 harmonic band pass filtering range

(a) 幅值解调信号

(b) 相位解调信号
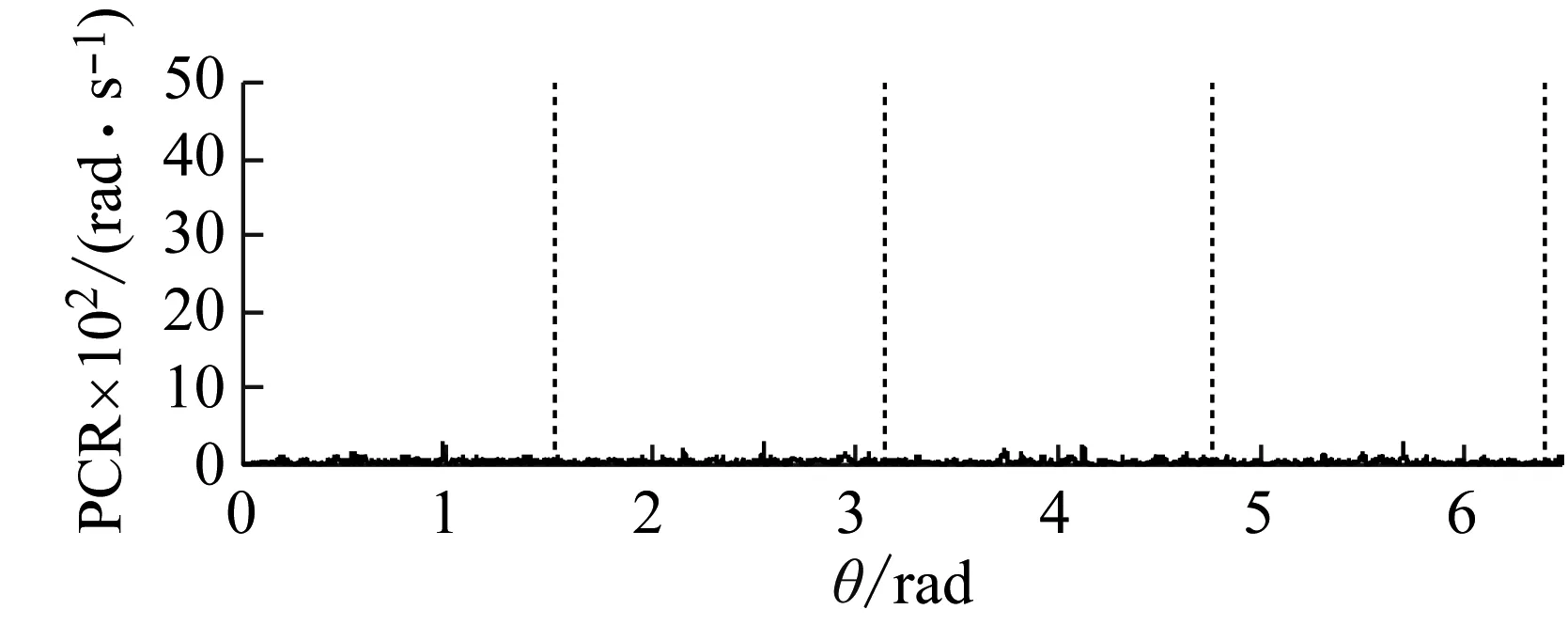
(c) 正常时相位变化率
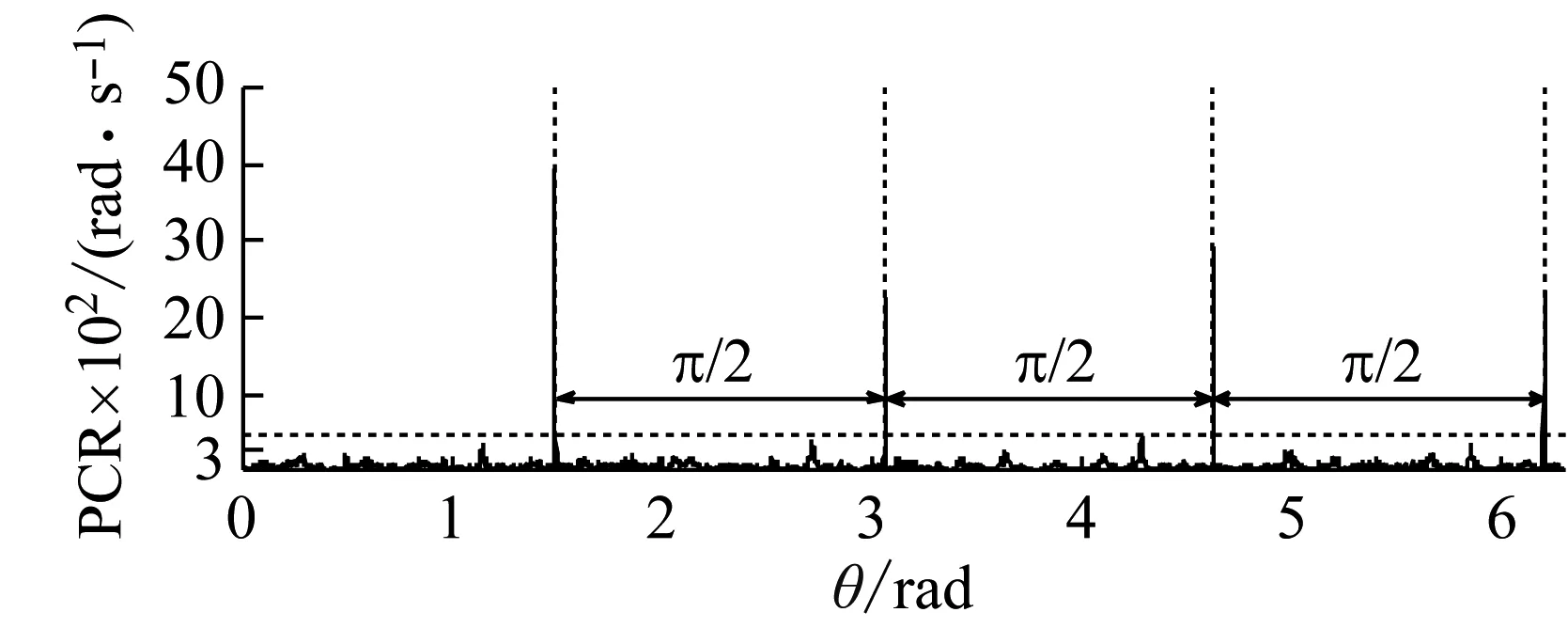
(d) 太阳轮故障时相位变化率图9 太阳轮IAS信号、振动信号及阶比谱Fig.9 IAS signal and order spectrum when solar wheel is normal
在工程实际应用中幅值与相位解调波形通常较为复杂,在相位解调波形中会出现多个与相位突变类似的位置,直接对相位解调波形进行观察不易对齿轮故障产生的相位突变进行判断,为此,研究中提出使用相位解调函数的相位变化率进行相位解调函数突变的增强判断,依据式(10)计算得到太阳轮正常与太阳轮齿根裂纹故障时相位解调函数的相位变化率如图9(c)、9(d)所示。
由表2中可知太阳轮故障特征阶比为4×,因此太阳轮故障周期为π/2。在图9(d)中太阳轮故障IAS信号的相位解调函数的相位变化率周期性的出现远高于其他位置的高峰值且相位突变且发生周期与故障周期一致,从图9(a)、(b)可以看出在相位变化率的峰值的位置上幅值解调函数出现负峰值、相位解调函数出现突变,由此可以判断太阳轮发生故障。而在图9(c)中太阳轮正常时相位解调函数的相位变化率无周期性高峰值出现。
4 结 论
(1) 实验结果表明,使用IAS信号对行星齿轮减速器太阳轮故障检测可以有效地克服振动信号受时变传递路径影响、低速工况等不足,为行星齿轮减速器故障检测提供了一种新方法。
(2) 基于峭度的解调频带选择策略可实现对含有丰富故障信息的频带进行选择;在窄带解调中使用相位解调函数的相位变化率可增强对相位突变的检测。

