基于自适应模型的在役斜拉桥时变力学性能追踪

孙华怀， 徐 俊， 陈惟珍

(1.扬州大学 建筑科学与工程学院，江苏 扬州 225127； 2.同济大学 桥梁工程系，上海 200092)

由于结构的复杂性，斜拉桥数值模型往往与实际结构存在一定的差异。在整个使用寿命期内，混凝土收缩、徐变和环境温度效应又始终影响着斜拉桥的力学性能[1]。故在役斜拉桥力学性能的数值评估结果往往与周期性现场检测不符。因此，如何根据周期性现场检测准确地追踪在役斜拉桥时变力学性能极具挑战。

以往文献表明，数值模型与实际结构通常存在3个方面的差异：模型结构误差，模型阶次误差和模型参数误差[2]。模型参数误差来自不精确的物理参数，也是斜拉桥数值模型与实际结构差异的主要来源[3]。为了消除模型参数误差，有限元模型修正技术已成为一种应用广泛且有效的桥梁结构分析工具[4]。有限元模型修正技术可分为直接法和迭代法两类。直接法根据测量数据重构结构整体质量和刚度矩阵。迭代法对模型中的物理参数进行修正。目前，使用最广的迭代法是基于灵敏度分析的有限元模型修正[5]。它通常被描述为一个优化问题，目标是将结构实测特性和模型计算结果间的差异最小化[6-8]。然而，上述研究通过多个误差函数的加权求和建立一个目标函数，并作为单目标优化问题。在此过程中，假设的权重因子代表不同目标之间的妥协，不能考虑个体目标间的冲突关系[9]。考虑个体目标间的冲突，多目标优化法随之被采用对桥梁有限元模型进行修正[10-11]。但他们的研究采用传统的基于梯度的优化算法求解派生的多目标优化问题。这些算法通常获得多目标优化问题的局部最优解，而不是全局最优解[12]。近年来，人工智能技术并被证明是求解优化问题的替代方法。因此，桥梁结构有限元模型修正问题的求解开始采用多目标优化进化算法，包括遗传算法[13-14]，神经网络算法[15]，粒子群优化算法[16]等。然而，上述研究仅考虑了斜拉桥模型的参数误差，却忽略服役阶段环境温度和混凝土时变效应。因此，斜拉桥力学性能的评估结果无法与周期性现场检测始终保持一致，也无法解释实测中斜拉桥力学性能的时变现象。

为了分析混凝土结构时变效应，研究人员提出了几种计算方法，如按龄期调整的等效弹性模量法、徐变率法和逐步数值法[17]。然而，仅少量的研究涉及考虑混凝土时变效应的斜拉桥结构分析。起初，研究重点是分析混凝土收缩、徐变对斜拉桥静力性能的时变效应，如应力、挠度和索力[18-20]。研究结果表明，在斜拉桥静力性能的评估中，需要考虑混凝土的时变效应。但他们的研究主要集中于斜拉桥静力性能。故Si等[21]考虑混凝土老化、徐变和收缩的影响研究了斜拉桥的动力性能。由于混凝土时变效应，斜拉桥自振频率随时间逐渐增加。混凝土时变效应在斜拉桥结构动力性能中同样起着重要作用。因此，研究者提出在斜拉桥设计阶段考虑混凝土时变效应。Lozano-Galant等[22]研究了混凝土徐变和收缩对斜拉桥服役阶段应力的影响，并提出了在斜拉桥设计阶段将混凝土时变效应计入目标服役阶段的方法。此外，为了达到理想的最终状态，Martins等[23]提出了考虑混凝土时变效应的斜拉桥索力的优化算法。然而，他们的研究都忽略了数值模型固有的参数误差。同时，鲜有研究考虑混凝土时变效应对在役斜拉桥时变力学性能进行数值追踪。

本研究分析服役阶段斜拉桥自适应模型的建立流程。根据斜拉桥设计资料，建立斜拉桥成桥时初始有限元模型。采用多目标优化法修正斜拉桥成桥时有限元模型。基于修正后的成桥有限元模型，考虑混凝土收缩、徐变及环境温度效应，建立斜拉桥服役阶段自适应模型，数值追踪在役斜拉桥长期荷载作用下的时变力学性能。同时，设计一座在役斜拉桥的周期性现场检测方案，对服役前2年该桥实际力学性能进行定期现场检测。

1 在役斜拉桥自适应模型

斜拉桥服役阶段，影响斜拉桥力学性能的因素较多，且各影响因素的作用时间域存在差别。混凝土收缩、徐变主要作用于构件开始受力后的三年内，拉索的退化主要发生在斜拉桥服役接近二十年的数年内，而环境温度效应则始终存在。为了有效分析斜拉桥时变力学性能，准确把握斜拉桥在服役特定时刻的结构状态，可建立斜拉桥自适应模型。斜拉桥自适应模型是考虑时变效应的有限元模型，通过已记录的结构历史行为、结构状态及环境信息，沿时间正向，从成桥状态开始，一直追踪到最近的桥梁检测时间节点处。首先，根据斜拉桥的档案信息资料，建立成桥时有限元模型，作为斜拉桥真实结构的初始模型。基于斜拉桥成桥时现场检测对斜拉桥初始有限元模型进行修正。基于修正的成桥模型，考虑服役阶段桥梁结构信息得到斜拉桥自适应模型，实现对各服役时间节点结构的真实模拟，如图1所示。

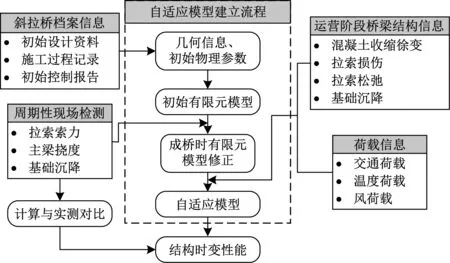
图1 斜拉桥自适应模型的建立Fig.1 Establishing adaptive models of cable-stayed bridges

2 在役斜拉桥时变力学性能数值追踪

2.1 基于灵敏度分析的斜拉桥有限元模型修正

基于灵敏度分析的有限元模型修正能够为斜拉桥建立准确的数值模型。为了保证数值结果与现场检测一致，通常建立多个目标函数，使得斜拉桥有限元模型修正成为一个多目标优化问题。因此，选取修正参数、建立目标函数和采用稳健的优化算法是三个关键步骤。

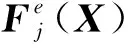
(1)

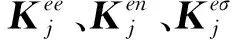
以斜拉桥成桥时全桥索力数值结果与现场实测值的差异为基础，构造标准化目标函数gi(X)为

(2)

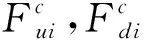
minimizeG(X)={g1(X),g2(X)}T

s.t.Ω={X|Xl≤X≤Xu}

(3)

式中，Xl、Xu和Ω分别是修正参数向量的下限、上限和可行域。

遗传算法是一种高效的随机搜索方法，并用于求解有限元模型修正问题的全局最优解。在求解时，遗传算法从多个可行解Xi(i=1 toNs,i∈N+)出发。这多个可行解的集合称为一个种群，记为pop(k)，k表示当前迭代步。种群中每个个体代表着多目标优化问题的一个可行解Xi。整个算法循环运行选择、交叉和变异三个遗传算子，直至适应度函数满足收敛条件，如图2所示。在求解式3的多目标优化问题时，遗传算法种群规模Ns设置为50。将交叉比Pc设为1.0，为下一种群提供足够的变异性。求解得到由m个非劣解组成的Pareto前沿Ω*={X1,X2,…,Xm}。从多目标优化问题的Pareto前沿Ω*中，根据距原点的欧氏距离为修正参数向量X选择一个最佳妥协解Xb。采用修正后的模型对斜拉桥成桥时力学性能进行数值评估。

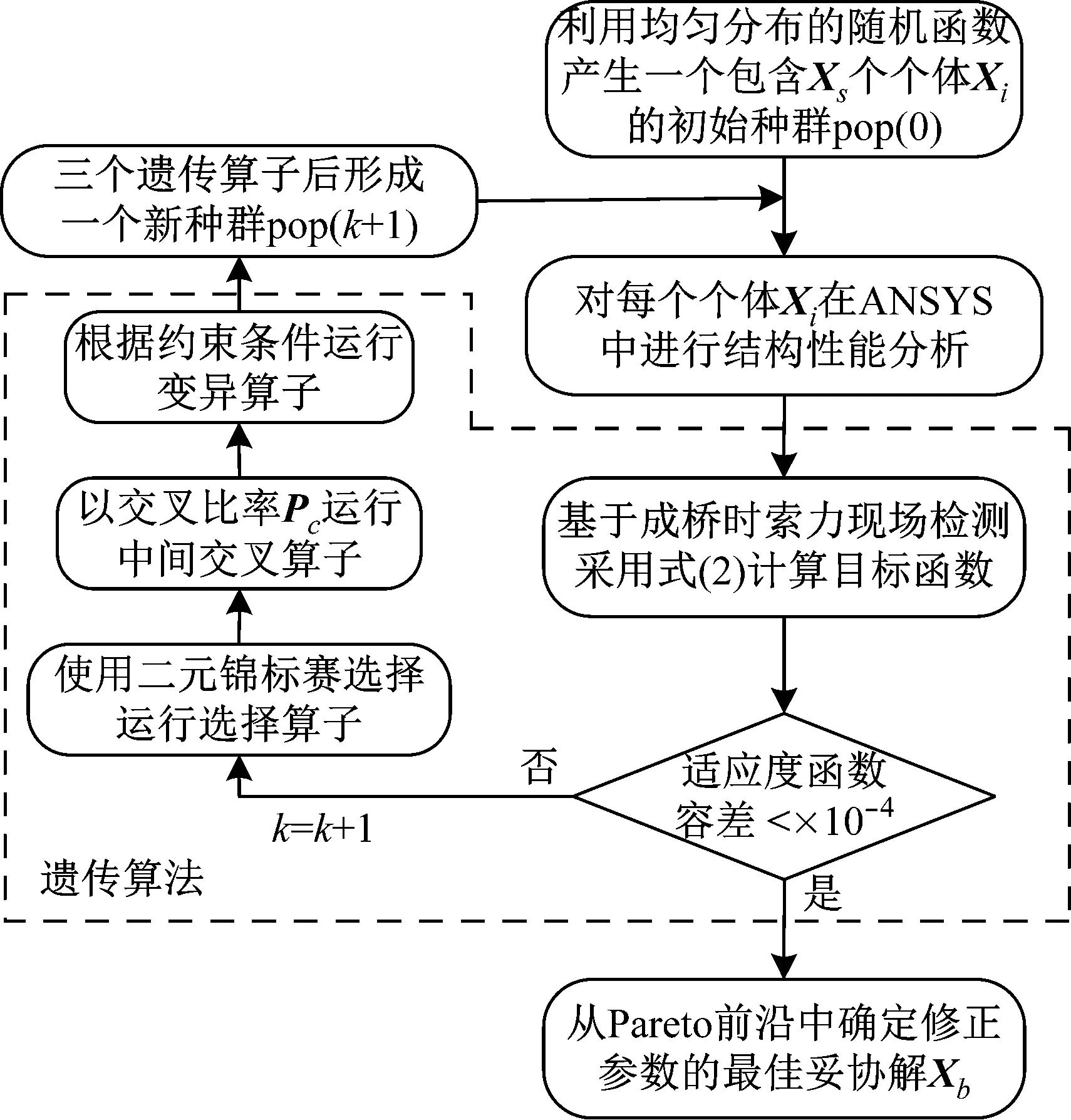
图2 遗传算法求解基于灵敏度分析的有限元模型修正Fig.2 Genetic algorithm for sensitivity-based finite element model updating

2.2 斜拉桥时变力学性能有限元逐步分析

(4)

表A.1 结构构件徐变和收缩模型中各参数细节Tab.A.1 Details of parameters in the creep and shrinkage model of structural members

(5)

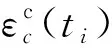
(6)

(7)

在数值分析时，斜拉桥的混凝土构件一般采用空间梁单元模拟。在第i个时间间隔Δti内，混凝土单元ele(ele=1 toNe, ele∈N+)的应变增量列阵Δεele(i)由四个部分组成

(8)

(9)

(10)

3 海河大桥结构及周期性现场检测

海河大桥(新桥)是一座钢-混凝土混合梁独塔斜拉桥。该桥全长490 m，主跨为310 m，边跨为180 m，全桥跨径组合为(310+2×50+2×40) m，如图3所示。主跨梁体采用钢箱梁与预应力混凝土箱梁混合结构，边跨采用预应力混凝土箱梁结构。混凝土箱梁为预应力结构，纵向预应力钢束采用7Φs15.20和9Φs15.20高强度低松弛预应力钢绞线。全桥上、下游共74根斜拉索，斜拉索采用直径Φ7半平行钢丝索。桥塔为钢筋混凝土双柱变截面结构。

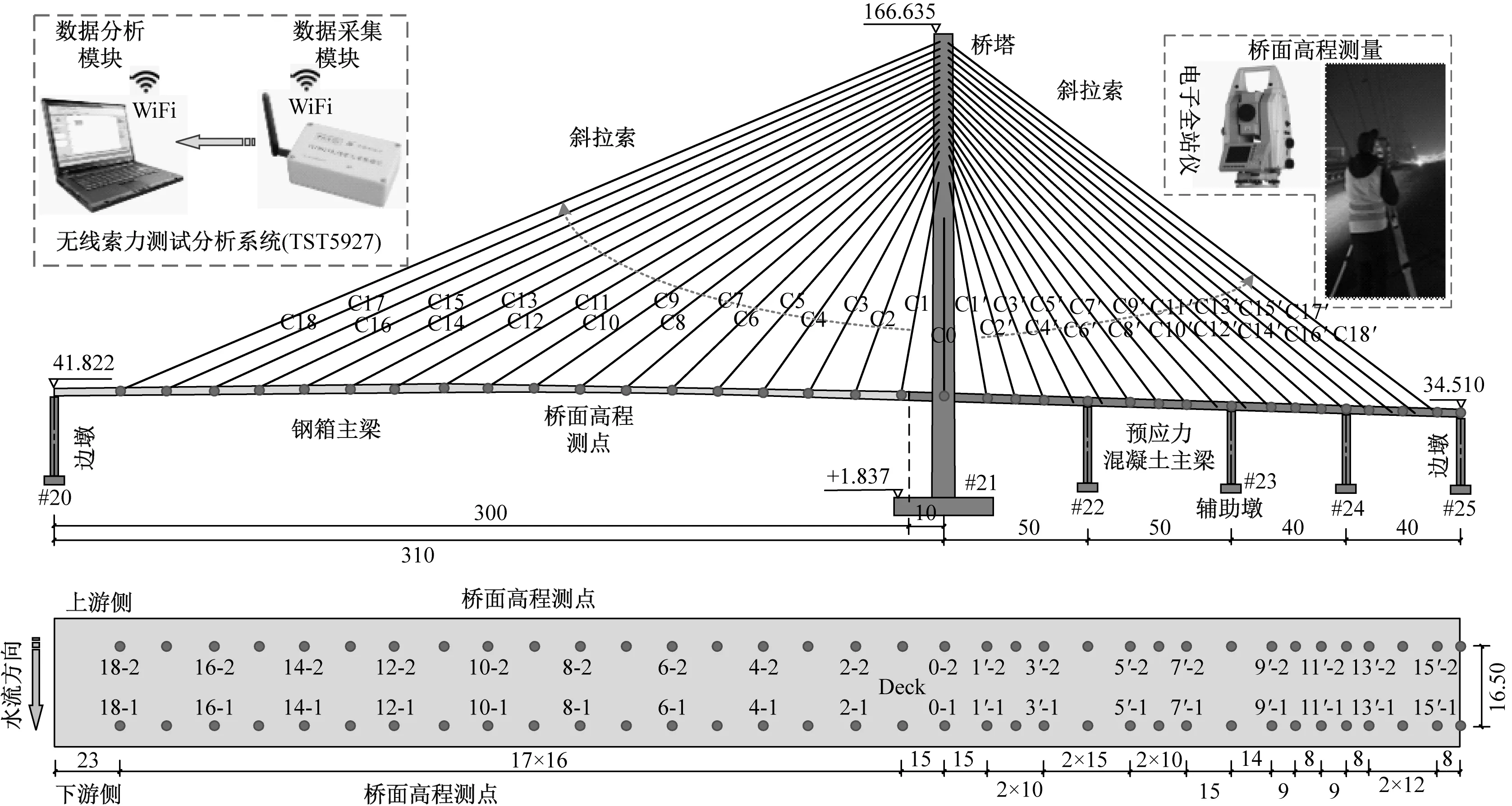
图3 海河大桥(新桥)结构及周期性现场检测方案(m)Fig.3 ConFiguration and periodic on-site inspections of Haihe Bridge (the new one) (m)

对海河大桥(新桥)主梁挠度和全桥索力进行定期检测。根据拉索纵向位置，主跨侧拉索编号为C1～C18，桥塔处0号拉索编号为C0，边跨侧拉索对应编号为C1′～C18′(图3)。桥面高程测点布置在桥面两端如图3所示，主桥上、下游各35个高程测点。高程测点编号从主跨至边跨为“M索号-侧”，上游侧记为“1”，下游侧记为“2”。斜拉索的索力采用无线索力测试分析系统(TST5927)进行检测。TST5927系统包括数据采集模块和数据分析模块(图3)。模块间的信号传递采用无线传输技术(WiFi)。TST5927系统的工作频率为0～50 Hz。数据采集模块配有16位A/D转换器，最大采样频率为200 Hz。桥面高程采用全站仪和精密电子水准仪进行测量。竣工后，对服役2年内该桥恒载作用下桥面高程、索力进行定期现场检测，具体检测时间及环境条件如表1所示。

表1 周期性现场检测具体时刻和环境条件细节Tab.1 Details of detection time and environmental conditions of periodic field measurements

4 海河大桥数值模拟和有限元模型修正

4.1 海河大桥(新桥)数值模拟

海河大桥(新桥)有限元模型包括桥塔、桥墩、主梁、斜拉索、预应力钢束、横隔板和支座等构件。桥塔和桥墩采用三维梁单元(BEAM188)模拟。混凝土主梁和钢主梁也采用三维梁单元(BEAM188)模拟。混凝土主梁BEAM188单元纵向尺寸与混凝土主梁节段长度一致(图4)。钢主梁BEAM188单元纵向尺寸为钢主梁节段长度的1(5(图4)。采用三维梁单元(BEAM4)模拟混凝土箱梁中预应力钢束。预应力效应通过对钢束单元施加初应变实现。预应力钢束单元通过刚度较大的三维梁单元(BEAM4)与主梁BEAM188单元的节点相连。混凝土箱梁和钢箱梁的横隔板模拟为138个集中质量单元(MASS21)。斜拉索采用三维杆单元(LINK10)模拟。拉索初始张拉力通过给拉索LINK单元施加初应变实现。拉索垂度采用等效弹性模量予以考虑。采用刚度较大的三维梁单元(BEAM4)连接拉索单元与主梁BEAM188单元。桥墩/主梁处的每个支座分别采用在X、Y和Z方向上三个独立的一维弹簧单元(COMBIN14)模拟。将全桥二期恒载模拟为均布线荷载，施加在主梁的梁单元上。环境温度变化模拟为温度荷载，并施加于全桥相应构件。海河大桥(新桥)有限元模型如图4所示。

图4 海河大桥(新桥)有限元模型细节Fig.4 Details of finite element model of Haihe Bridge (the new one)

4.2 海河大桥(新桥)有限元模型修正

由于钢箱梁内形状复杂的加劲肋和辅助设施，很难使模拟的钢箱梁截面(图4)与设计截面完全一致。钢箱梁节段的截面刚度和自重较初始设计值略有下降。因此，将钢箱梁材料的弹性模量和密度(即x1和x2)作为修正参数。考虑构造钢筋的影响，模型中混凝土桥塔(即x3和x4)、桥墩(即x5和x6)和主梁(即x7和x8)材料的弹性模量和密度也选为修正参数。混凝土箱梁和钢箱梁的横隔板的计算质量通常会与实际情况存在差异。因此，混凝土箱梁(即x9～x11)和钢箱梁(即x12～x14)的横隔板质量也需要修正。桥面附属设施将对二期恒载产生一定的影响，故二期恒载(x15)也作为修正参数。已采用等效弹性模量考虑拉索垂度效应并计入护套重量，斜拉索的弹性模量和材料密度不作为修正参数。成桥时拉索的索力检测存在误差，斜拉索张拉力(即x16～x52)作为修正参数。主梁/桥墩的连接弹簧刚度的计算值往往支座的实际刚度不一致。模型中主梁/桥墩连接弹簧刚度(即x53～x64)也作为修正参数。

根据式(1)对预选的修正参数进行索力灵敏度分析。结果表明，修正参数x2(钢箱梁材料密度)具有最大的无量纲的索力灵敏度，数值为0.41。这是因为钢箱梁密度的变化会引起主跨各拉索索力的变化。修正参数x16～x52(拉索C18～C18′初始张拉力)的无量纲索力灵敏度差异很小，在0.04～0.07。全桥索力对主梁/桥墩连接弹簧刚度(即x53～x64)不敏感，无量纲索力灵敏度数值接近为0。为保证模型修正的效率，去除修正参数x5和x6(辅助墩材料特性)、x10(混凝土箱梁横隔板)、x14(钢箱梁横隔板)、x53～x64(主梁/桥墩连接弹簧刚度)。最后，得到一个48维的待修正参数向量X。

以各修正参数的设计值作为有限元模型修正过程中的初始值(表2)。基于成桥时现场实测索力按式(2)构造目标函数。根据斜拉桥施工中的不确定性和工程结构数值分析经验，每个修正参数设有±10%的变化范围(表2)，以保证模型修正过程中各修正参数的物理意义。采用遗传算法求解，733代后得到含有22个非劣解的Pareto前沿Ω*={X1,X2,…,X22}。由距原点的欧氏距离，选择Pareto前沿Ω*中非劣解X13的作为修正参数的最佳妥协解Xb。模型修正前，目标函数g1(X)和g2(X)初始值分别为6.87%和6.50%。修正后，目标函数g1(X)和g2(X)计算值分别下降为1.06%和1.23%，且非劣解X13将导致下游侧拉索索力与实测值的相对差异略大一些。对于非劣解X13，部分参数的具体修正细节如表2。模型修正后，各构件材料特性和二期恒载的修正值与初始值的相对变化均在±10%范围内。各构件材料特性和二期恒载的修正值均大于初始值。这是由于初始有限元模型中忽略形状复杂的肋、混凝土构件的构造钢筋和一些辅助设施，各构件材料特性和二期恒载的修正值补偿了截面刚度和质量的损失。模型修正后，全桥拉索张拉力修正值与初始值的相对变化均在±10%范围内(见附表A.2)。拉索C3张拉力的修正值拥有最大的相对变化，为10%。拉索C0张拉力的修正值拥有最小的相对变化(-4.7%)。同时，从附表A.2中可以发现，全桥大部分拉索张拉力的修正值大于初始值。

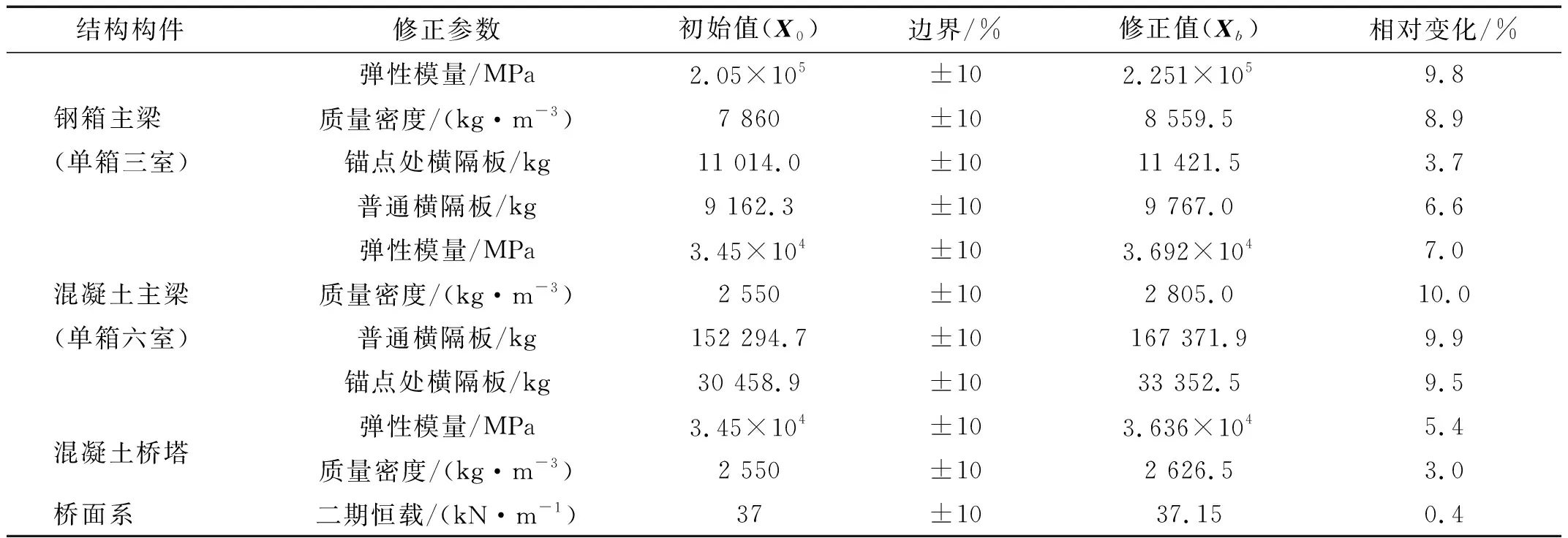
表2 修正参数初始值和修正值细节Tab.2 Initial and updated details of updating parameters

5 海河大桥(新桥)时变力学性能

基于斜拉桥自适应模型，数值评估海河大桥(新桥)服役1年和2年后时变力学性能。

5.1 服役1年后力学性能

以服役1年后现场实测索力为基准，图5(a)和图5(b)分别分析了上、下游索力初始有限元计算结果和自适应模型计算结果与实测值的相对差异。全桥索力初始有限元计算值普遍小于服役1年后索力现场实测值。上游侧索力初始有限元计算结果与实测索力的相对差异在-15.31%～-4.16%。下游侧索力初始有限元计算结果与实测索力的相对差异在-15.05%～-2.00%。基于自适应模型，上游侧索力计算值与实测索力的相对差异缩小在-6.31%～2.48%之内如图5(a)所示。下游侧索力有限元计算值与实测索力的相对差异缩小在-6.31%～3.01%之内如图5(b)所示。服役1年后，全桥拉索中上游侧拉索C0的索力计算结果与实测索力相对差异最大，具体数值为-10.0%。

(a) 上游侧

(b) 下游侧图5 服役1年后实测与计算索力相对差异Fig.5 Relative difference of measured and calculated cable forces after 1 year in service

图6描述了服役1年后海河大桥(新桥)主梁挠度初始有限元模型结果、自适应模型数值结果及现场检测结果。以桥面设计高程为参考基准值，计算了成桥状态和服役1年后主梁挠度的实测结果。数值结果及现场检测均表明，服役1年后，该桥主跨主梁挠度较大，而边跨主梁由于辅助墩的作用挠度较小。根据周期性现场检测，成桥至服役1年间，主跨主梁高程测点M13处挠度向下增加了0.063 m，桥塔处主梁高程测点M0处挠度向下增加了0.015 m。服役1年后，主跨主梁实测挠度最大值为-0.202 m(高程测点M13处)。主梁最大挠度初始有限元模型计算结果为0.098 m，位于M14测点。基于自适应模型，主跨主梁最大挠度数值计算值为-0.225 m，纵向位置位于桥面高程测点M12处。桥塔处主梁(高程测点M0处)挠度实测值和数值结果基本一致，分别为-0.022 m和-0.026 m。全桥主梁挠度实测值和自适应模型数值结果最大差异为-0.025 m。

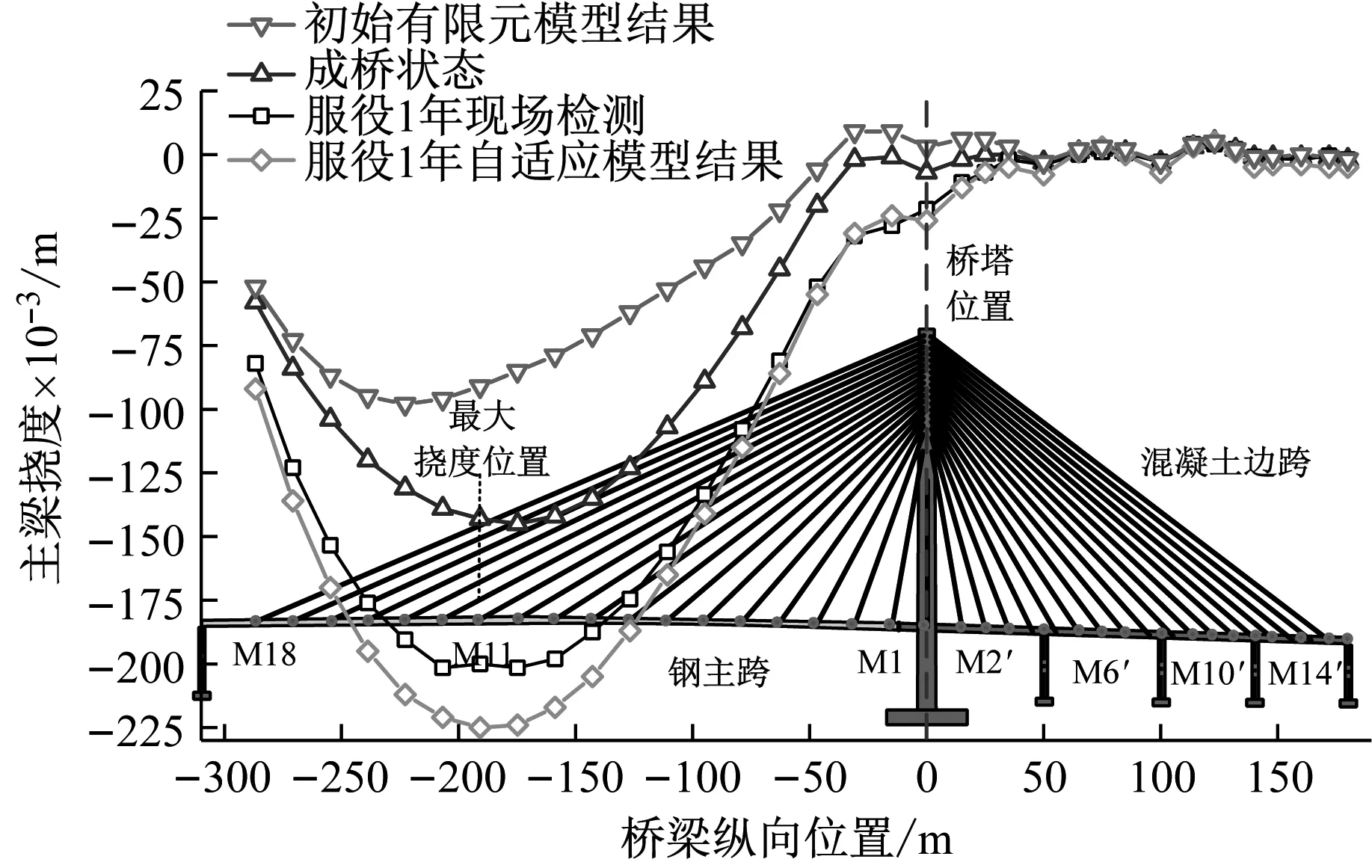
图6 服役1年后主梁挠度检测结果与数值计算结果Fig.6 Measured and calculated girder deflections after 1 year in service

5.2 服役2年后力学性能

以服役2年后现场实测索力为基准，图7(a)和图7(b)分别分析了上、下游索力初始有限元计算结果和自适应模型计算结果与实测值的相对差异。全桥索力初始有限元计算值普遍小于服役2年后索力现场实测值。上游侧索力初始有限元计算结果与实测索力的相对差异在-16.49%～-1.43%。下游侧索力初始有限元计算结果与实测索力的相对差异在-17.36%～-1.12%。基于自适应模型，上游侧索力计算值与实测索力的相对差异缩小在-9.02%～3.58%之内如图7(a)所示。拉索C0索力计算结果与实测索力相对差异最大。下游侧索力计算值与实测索力的相对差异缩小在-8.28%～3.94%之内如图7(b)所示。服役2年后，全桥拉索中上游侧拉索C0索力计算结果与实测索力相对差异最大(-9.02%)。

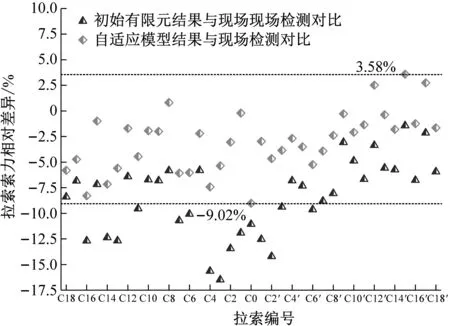
(a) 上游侧

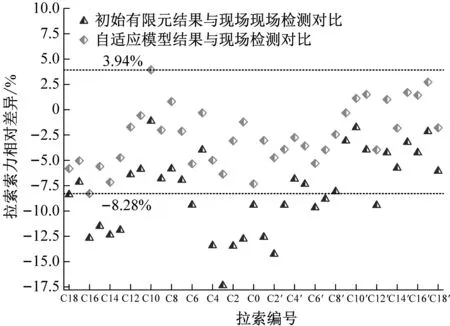
(b) 下游侧图7 服役2年后实测索力与计算索力相对差异Fig.7 Relative differences of measured and calculated cable forces after 2 years in service

图8描述了服役2年后主梁挠度数值结果及现场检测结果。以桥面设计高程为参考基准值，计算服役2年后主梁挠度的实测结果。同样，服役2年后，该桥主跨主梁挠度较大，而边跨主梁挠度较小。根据周期性现场检测，成桥至服役2年间，主跨主梁高程测点M13处挠度向下增加了0.088 m，桥塔处主梁高程测点M0处挠度向下增加了0.021 m。服役2年后，主跨主梁实测挠度最大值为-0.230 m，纵向位置位于桥面高程测点M11处。主梁最大挠度初始有限元模型计算结果为0.098 m，位于M14测点。基于自适应模型，主跨主梁最大挠度数值计算值为-0.240 m，纵向位置位于桥面高程测点M12处。桥塔处主梁(高程测点M0处)挠度实测值和数值结果分别为-0.028 m和-0.026 m。全桥主梁挠度实测值和数值结果最大差异为-0.013 m(高程测点M12处)。

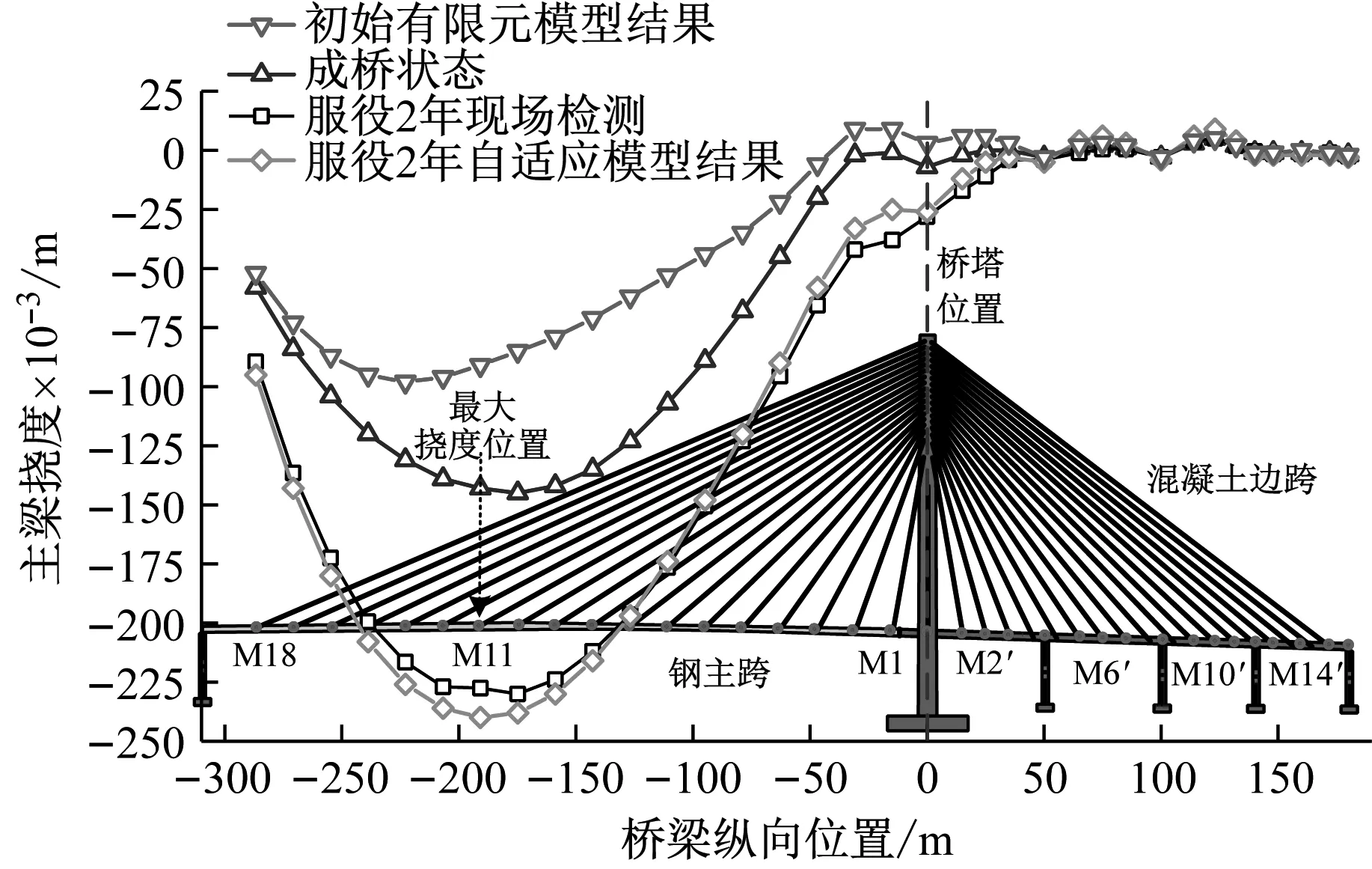
图8 服役2年后主梁挠度检测结果与数值计算结果Fig.8 Measured and calculated girder deflections after 2 years in service

服役1年和2年后，全桥索力数值计算结果与实测索力相对差异最大的均是上游侧拉索C0。这可能是由于海河大桥(新桥)是漂浮体系，全桥拉索中桥塔处拉索C0的初始张拉力最大(见附表A.2)。服役1～2年内，全桥主梁挠度自适应模型计算结果与实测值间的最大差异从0.025 m降为0.013 m。这可能是由周期性现场检测的随机误差和桥梁服役性能退化所共同导致。

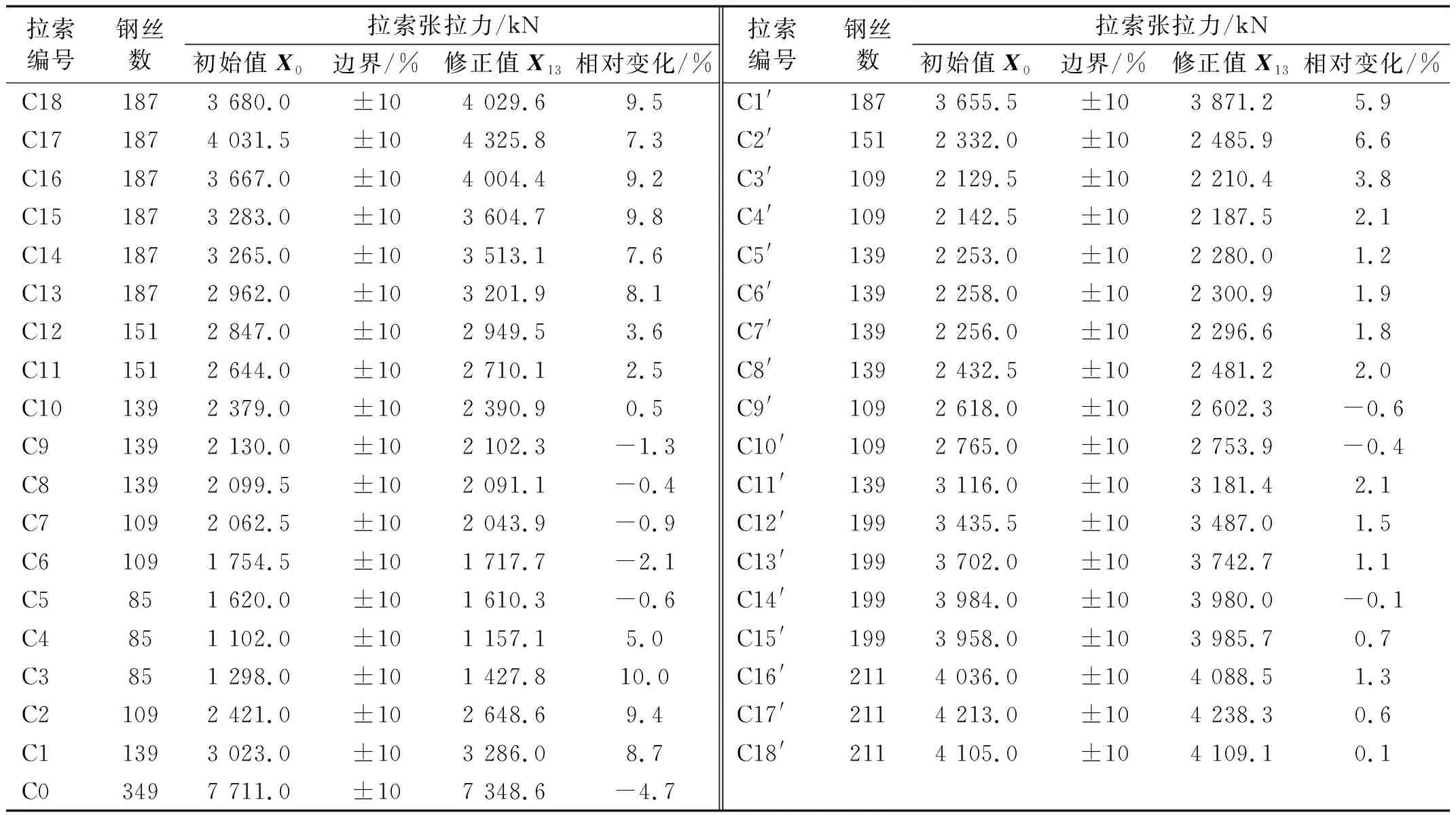
表A.2 拉索张拉力初始值和修正值细节Tab.A.2 Details of initial and updated cable tension forces

6 结 论

基于服役阶段斜拉桥自适应模型，数值评估了海河大桥(新桥)服役1年和2年后的时变力学性能，并与周期性现场检测进行了对比，得到以下几点结论：

(1) 服役1年和2年后，海河大桥(新桥)全桥索力初始有限元结果与实测值的相对差异分别达-15.31%和-17.36%，实测主梁最大挠度分别向下增加了0.063 m和0.088 m。初始有限元模型评估在役斜拉桥力学性能会存在超出10%的相对误差，且无法追踪斜拉桥时变力学性能。

(2) 基于自适应模型，海河大桥(新桥)全桥索力数值结果与周期性现场检测值的相对差异始终保持在±10%之内。服役1年和2年后，主梁挠度数值结果和实测值最大差异分别为-0.025 m和-0.013 m。服役阶段斜拉桥自适应模型能够有效追踪在役斜拉桥时变力学性能，且数值结果与实测值的相对差异保持在10%以内。

(3) 自适应模型的数值结果表明，服役阶段海河大桥(新桥)主跨主梁挠度逐渐增大，边跨主梁挠度变化较小。服役1年和2年后，主跨主梁最大挠度数值结果分别为-0.225 m和-0.240 m，桥塔处主梁挠度数值结果均为-0.026 m。

本文主要研究在役斜拉桥时变力学性能数值追踪方法这一复杂的实际工程问题。海河大桥周期性现场检测数据用于有限元模型修正及自适应模型验证。实际上，现场检测存在传感器测试噪声和检测误差，且与环境条件(风、温度、交通荷载)和技术人员水平相关。由于目前索力实测数量有限，本研究未对索力实测数据的精度进行分析。后期将持续收集索力长期检测数据，研究基于索力检测不确定性的斜拉桥有限元模型修正方法。

附录A