空间小净距交叉隧道动力响应振动台试验研究
雷 浩, 吴红刚, 钱建固, 赖天文, 纪志阳, 梁 彧
(1.同济大学 地下建筑与工程系,上海 200092;2.中铁西北科学研究院有限公司,兰州 730070;3.兰州交通大学土木工程学院,兰州 730070)
立体交叉隧道因其受地形及选线限制小,同时具有良好的经济效益和施工条件而被广泛应用。如丹大铁路前阳至庄河段出现“立体交叉隧道群”,既有及拟建铁路与铁路、公路与公路、铁路与公路隧道交叉多达11处[1]。立体交叉隧道相较于单洞隧道而言,具有隧道间穿越风险大、多重效应耦合明显、环境效应多次叠加、变形难以控制等特点[2]。
以往在对立体交叉隧道的研究中,学者们主要对交叉隧道的施工力学特性进行了讨论,且已在力学特性分布、加固技术及监控量测等静力学方面取得了丰硕的研究成果[3-5]。而立体交叉隧道在动力学方面的研究起步较晚,目前主要集中在爆破影响、列车荷载及地震响应等方面:Lai等[6-8]采用爆破振动监测系统和数值模型来监测新建隧道施工爆破振动对既有隧道结构的影响;王海龙等[9-10]对交叉隧道在列车激励及轴重荷载作用下的影响规律进行了研究。对于立体交叉隧道在地震方面的研究,王国波等[11-12]通过对大量近距离相互穿越隧道工程的地震响应归纳整理,总结分析不同结构体系的动力响应特点和后期研究重点方向;Chen等[13-15]通过不同数值软件建立三维模型分别对盾构地铁隧道及连拱隧道进行动力模拟,结果表明在地震荷载作用下隧道之间存在相互影响作用,同时也开展振动台试验对数值模拟结果进行了验证。
通过上述研究发现,国内外学者对于立体交叉隧道的研究多集中于施工力学方面,在动力学方面的研究也以爆破及列车等动荷载为主。但有研究表明地震荷载对土-结构所产生的动力影响相较其余两种动荷载来说更为复杂,且所诱发的破坏也更为严重[16]。同时,由于地震荷载的未知性和不可控性,导致立体交叉隧道的震害风险更加难以预测和控制。目前,采用模型试验对立体交叉隧道的地震响应研究较少,Lei等[17]及Liu等[18-19]开展振动台试验对立体交叉隧道结构的动力响应特性进行初步探讨及分析。同时对立体交叉隧道动力学中地震波频谱特性的研究也较少。
鉴于此,为研究立体隧道在地震荷载作用下的动力响应及其频谱特性,以某空间小净距立体隧道工程为对象,通过振动台试验对隧道的应变及围岩的加速度等动力响应进行分析。同时引入反应谱理论对结构动力与地震动之间的关系进行了研究,研究结果以期为此类空间交叉隧道的抗震设计提供相应理论参考。
1 试验工点概况
本次振动台试验以辽宁省某立体交叉隧道群为工程背景,选取某铁路隧道上跨公路隧道为研究对象,两隧道相交处轨面高差为14.19 m,交叉影响段隧道埋深约为65 m,两隧道结构净距为4.24 m,为空间斜交型立体隧道,空间位置如图1所示。根据TB 10003—2016《铁路隧道设计规范》[20]及JTG 3370.1—2018《公路隧道设计规范》[21]所规定的隧道近接交叉施工相互影响范围及分类可知,两隧道净距为4.24 m<1.0B(B为洞宽,取10 m),处于需采取相关措施的范围内,属于超小净距立体交叉隧道。

图1 立体交叉隧道空间位置Fig.1 Schematic diagram of spatial location of overlapped tunnel
通过前期勘探及超前地质预报表明,隧道交叉区段岩层主要以混合花岗岩为主,交叉段地质探测围岩波速Vs为1 000 m/s,Vp为2 600 m/s,查阅规范表明交叉区段围岩为IV级围岩,场地区处于VII级(地震波峰值为0.15g)地震基本烈度范围内。
2 振动台模型试验设计
隧址区有多处交叉近接工程,为了充分研究空间交叉隧道的动力响应,在综合考虑隧道位置、埋深及断面尺寸后,选取具有典型代表性的正交型及斜交型立体隧道为研究对象。试验设计左幅为正交型立体隧道,右幅为斜交型立体隧道,如图2所示。因斜交型空间立体隧道净间距较小、围岩条件较差,在立体交叉隧道工程中具有较强的代表性,故本文主要研究右幅空间斜交型立体隧道的动力响应。

图2 模型示意图(m)Fig.2 Model diagram (m)
2.1 相似关系及模型材料设计
根据立体交叉隧道的动力相互作用及系统组成,并综合考虑试验条件,最终选取几何相似比CL=1/50、密度相似比Cρ=1及弹性模量相似比CE=1/30为基础控制参数。基于Buckingham π相似定理[22],推导出其余参数相似关系和相似比分别为
CH=CD=CL=1/50
(1)
Cσ=Cc=CE=1/30
(2)
Cφ=Cμ=Cε=Cρ=1
(3)
式中:ρ为密度;H为隧道埋深;D为隧道洞宽;L为模型长度;σ为应力;ε为应变;E为弹性模量;φ为内摩擦角;c为黏聚力;μ为泊松比。
试验中选取Ⅳ级围岩为研究对象,选择水泥、粗砂、土、石膏、石英砂及水等来制作模型材料,并按照相似关系对混合材料进行相关室内试验,最终测得围岩及隧道衬砌相关参数如表1所示。根据相似比换算,各参数基本满足规范对Ⅳ级围岩的要求。

表1 原型及模型物理力学参数对比[23]Tab.1 Comparison of physical and mechanical parameters between prototype and model[23]
2.2 测试元件布设
为了研究立体交叉隧道结构的应变响应并对比有无隧道交叉段/非交叉段围岩周围的动力响应,试验中主要在隧道结构的典型位置布置相应动应变片,并在坡体内部布置若干加速度传感器,如图3所示。其中,上跨(下穿)隧道动应变计编号为S1~S6(X1~X6),坡体内部非交叉段加速度传感器编号为PA1~PA8,交叉段加速度传感器编号为TA1~TA8。其中,II(II’)为交叉断面,I及III(I’及III’)为两侧影响区断面。
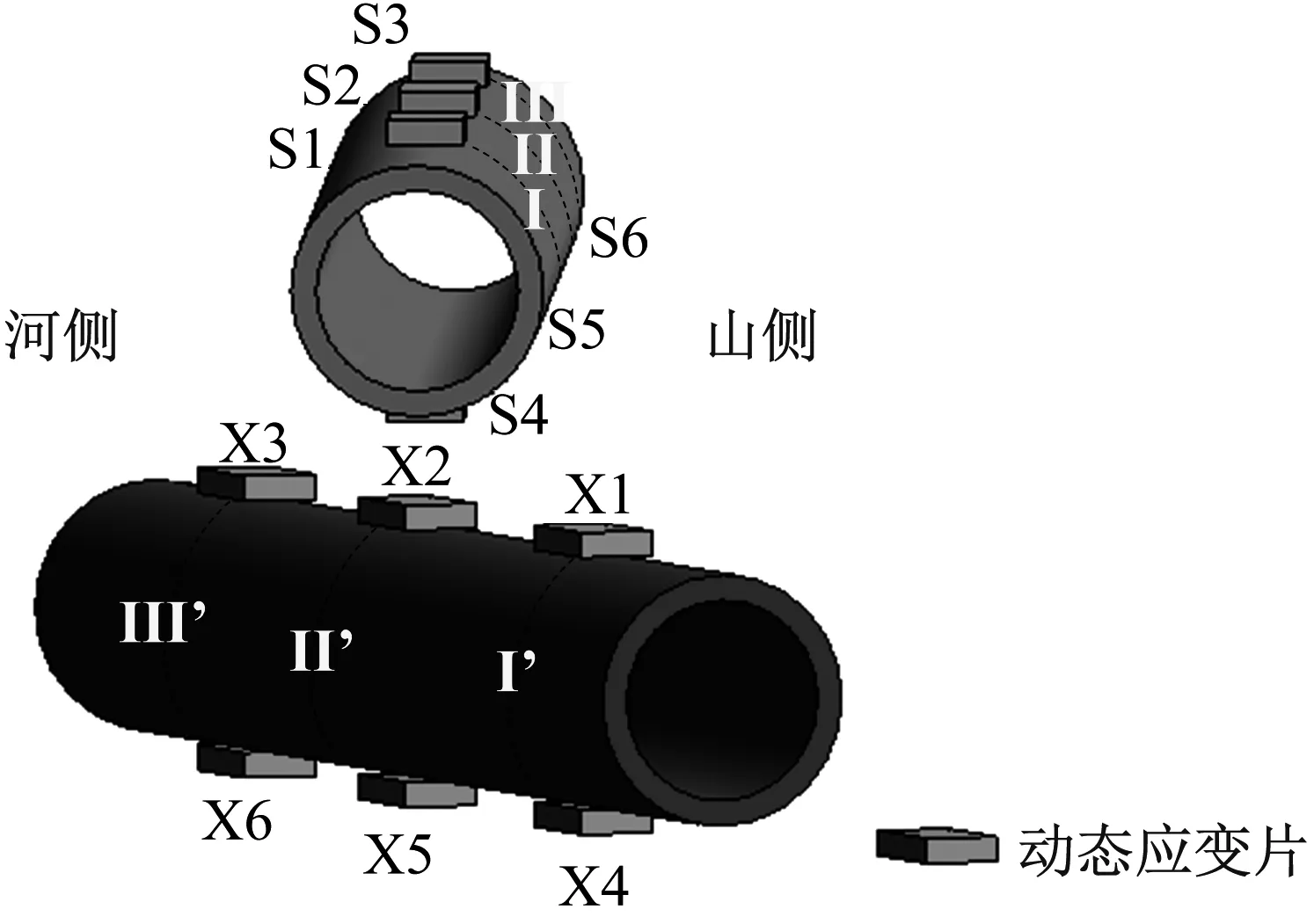
(a) 动态应变片

(b) 加速度传感器图3 测试元件布置(mm)Fig.3 Test element arrangement (mm)
试验中采用三相电容式加速度传感器,灵敏度为680 mV/g,测量范围为±2g,尺寸为13 mm × 15 mm × 8 mm。动应变片的灵敏度系数为2.0~2.2,温度容许范围为-30~80 ℃,其尺寸为15.5 mm×5.0 mm。为了防止温度及导线长度对输出应变信号产生影响,因此对应变片进行补偿以减小误差,如图4所示。

图4 动应变片补偿Fig.4 Dynamic strain gauge compensation
2.3 边界处理及模型填筑
试验中采用振动台系统所配套的刚性模型箱,考虑到模型箱边界效应会影响试验结果,在试验中采取以下措施减小边界效应:①在模型箱水平振动方向设置一层50 mm厚的高强度聚苯乙烯塑料泡沫板,以模拟截断介质土体对有限域土体介质的弹性支持作用[24];②为了减少模型箱侧壁及箱底的摩擦,试验箱两侧均匀涂抹凡士林并在箱底铺设粗砂碎石材料,将其处理成摩擦边界;③为了防止结构受模型箱的影响而产生振动,在隧道两端洞口分别放置一层聚苯乙烯塑料泡沫板,减小振动波的反射。通过分析比较不同测点在同一工况下相应的加速度时程及傅里叶谱曲线,发现其曲线形式、频谱成分组成及幅值都较为相似,说明采用泡沫板的效果较为理想,能减少边界上部分地震波的散射与折射[25],使地震波具有良好的保真性。
在右幅立体交叉隧道中,两隧道在空间中以小角度相交,交角为20°,根据隧道埋置深度及相似关系(1∶50),模型中上跨隧道埋深为100 cm,下穿隧道埋深为92 cm,两隧道净间距为8 cm(原型为4.24 m)。下穿隧道斜向放置,上跨隧道沿模型箱纵向放置,试验中上跨隧道可见。围岩相似材料采用分层填筑,每一层填筑完成时选取不同位置处围岩相似材料,对其密度及含水率进行复测以保证土体参数由上至下的一致性;在填筑至指定位置后埋设相应的传感器,模型填筑过程具体步骤如图5所示。

(a) 隧道埋置

(b) 分层填筑

(c) 传感器埋设

(d) 模型完成图5 模型填筑过程Fig.5 Model filling process
2.4 加载制度设计
试验中主要输入的地震波为水平向(X向)El-Centro波,地震波峰值加速度为0.1g时其时程曲线及傅里叶谱如图6所示。

(a) 加速度时程

(b) 傅里叶谱图6 El-Centro波时程曲线及傅里叶频谱图Fig.6 Time-history and Fourier spectrum of El-Centro wave

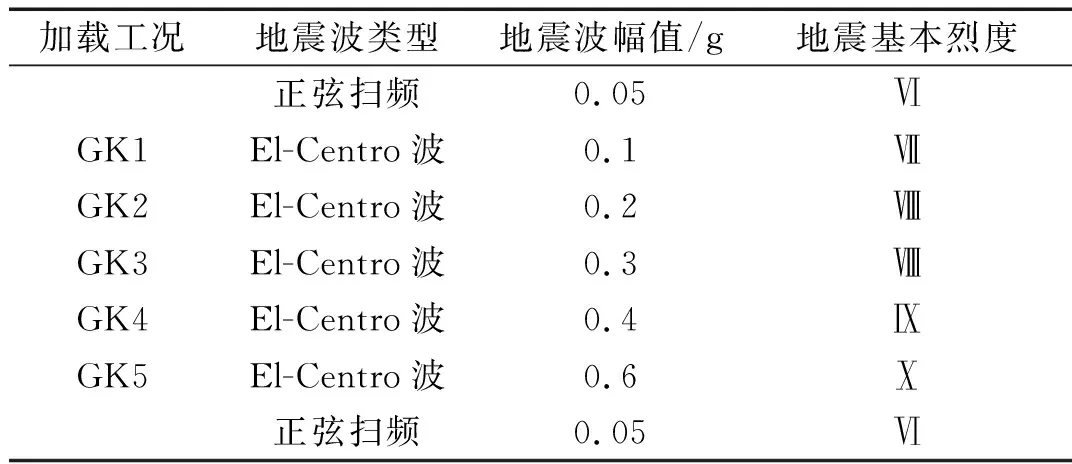
表2 地震波加载顺序Tab.2 Loading sequence of seismic wave
3 振动台试验结果分析
3.1 隧道动应变响应
为探究交叉隧道应变响应的分布规律,对上跨及下穿隧道轴向的应变峰值及其时程曲线进行了分析。
3.1.1 应变峰值
图7为上跨隧道各测点在不同地震荷载作用下的应变峰值。一般在均匀地震动激励下,隧道纵向各测点的动力响应在理论上应该是相同的[27],但试验测试结果却表现出较大差异。随输入地震波峰值的增大,上跨隧道的拱顶及仰拱轴向应变表现出明显的非线性增长特点。在较小地震荷载作用下(0.1g~0.2g),上跨隧道的轴向应变响应大小分布规律基本呈“交叉断面→两侧影响区断面”演化,即S2测点的应变峰值均大于S1及S3测点。而当地震加速度峰值超过一定界限时(0.4g),隧道结构以“影响区断面→交叉断面→影响区断面”的形式产生震害破坏,即S2测点的应变峰值均小于S1及S3测点。

图7 上跨隧道应变峰值分布规律Fig.7 Peak strain distribution of the upper-span tunnel
图8为下穿隧道各测点在不同地震荷载作用下的应变峰值。下穿隧道拱顶各测点应变峰值随输入地震波峰值的增加,呈先增大后减小的趋势,并最终保持稳定;隧道拱顶轴向应变峰值在交叉断面II处均大于其余两侧断面,这说明地震波由于其空间效应及传播特性在拱顶处产生应变的“叠加效应”,导致该点的地震响应较大,易成为抗震环节中的薄弱区。仰拱断面II’的应变峰值未出现明显的增长规律,交叉断面X5测点的应变峰值在加载过程中基本保持不变。这也说明在地震荷载作用下隧道仰拱具有良好的稳定性,这个现象在胡建平等[28]采用数值模拟分析的结果中也有所体现。而X6测点的应变响应表现有所不同,其随加载地震波峰值的增大开始缓慢增加随后剧烈增加,在0.6g时达到最大为46.62 με。

图8 下穿隧道应变峰值分布规律Fig.8 Peak strain distribution of the under-crossing tunnel
将两隧道I~III(I’~III’)断面沿轴向动应变峰值提取出来,如图9所示。图中左幅为上跨隧道轴向应变峰值结果,右幅为下穿隧道轴向应变峰值结果;上X轴及右Y轴为拱顶动应变峰值,下X轴及左Y轴为仰拱动应变峰值。
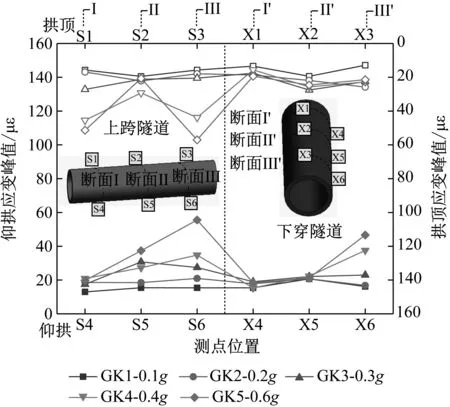
图9 轴向应变响应对比图Fig.9 Comparison diagram of axial strain response
由图9可以看出,拱顶及仰拱轴向应变峰值随地震波峰值的变化而产生的规律较为相似,但上跨隧道的应变动力响应整体大于下穿隧道。其原因是在地震过程中由于上部土体的挤压导致其更容易发生变形,同时由于上跨隧道的影响及围岩的挤密效应,减弱地震波对于下穿隧道的冲击,对其地震响应有一定的削弱作用。此外,在断面III处,即S3和S6处出现“锯齿状”分布,且在仰拱处表现的更为明显;同样的现象在X6所在的断面III’处也有所体现,这说明靠近河侧及临空面的断面(III及III’)在地震荷载作用下应变动力响应较为强烈,表明应变动力响应沿水平向具有显著的“趋表特性”,即沿着临空面方向其放大效应逐渐增大,易成为隧道结构潜在的破坏区。
3.1.2 时程曲线
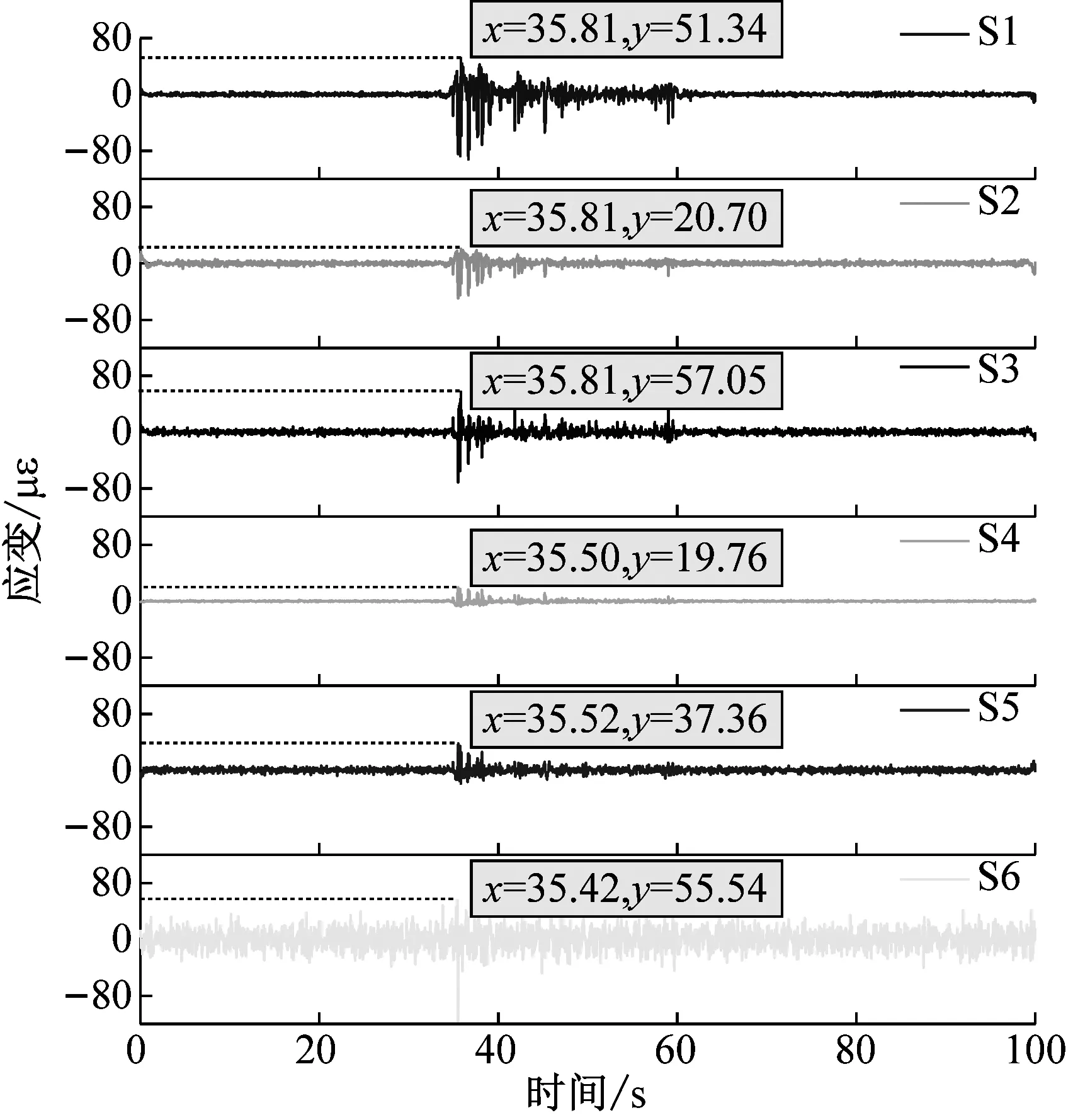
图10为0.6gEl-Centro波作用下各测点的应变时程曲线。上跨隧道轴向测点时程曲线的波形基本表现一致;而下穿隧道轴向测点时程曲线的波形表现出明显的差异性。同时,下穿隧道的应变响应基本都小于上跨隧道,这也表明了在强震作用下上跨隧道衬砌更易产生损伤甚至会发生破坏。

(a) 交叉段
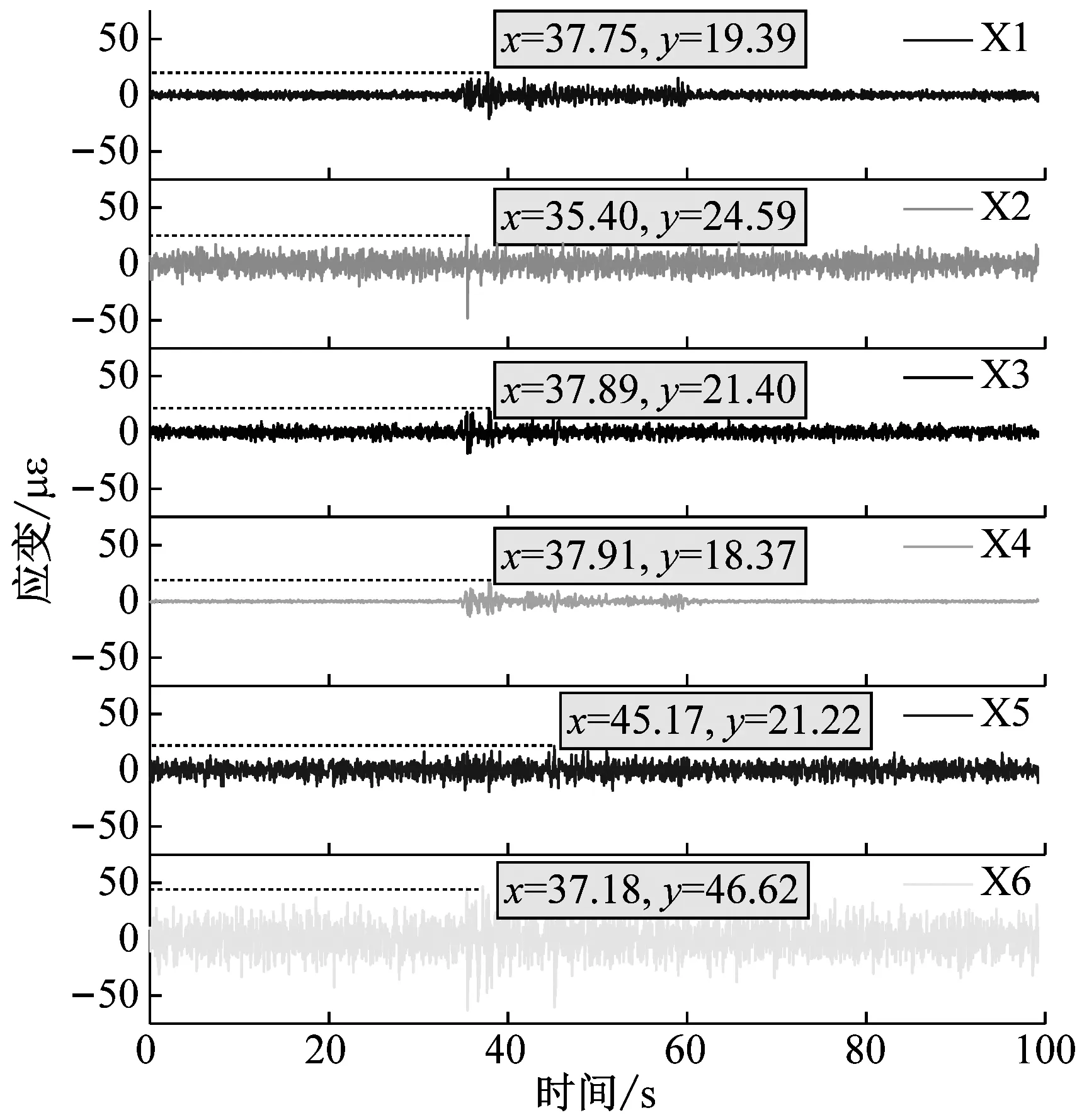
(b) 下穿隧道图10 隧道应变时程曲线Fig.10 Time-history of strain curve of tunnels
上跨隧道各测点达到峰值的时间基本维持在35 s左右,而下穿隧道各测点出现了峰值滞后现象,其达到峰值的时间基本在37 s左右。这是由于在地震波传播过程中,隧道结构及围岩的阻尼发挥了作用,延缓了地震波达到峰值的时间,同时在这个过程中上跨隧道及围岩也吸收了部分能量,导致下穿隧道所受到的地震响应相对较小。因此在高烈度地震区的立体交叉隧道工程中,其上跨隧道可能会更早出现破坏且破坏也更为严重。这也说明在地震荷载累积作用下,地震波传递过程中在隧道不同位置处的能量损耗程度不同,从而导致结构的破坏具有一定的“滞后性”,这也应是将来立体交叉隧道抗震设计所关注的重点问题。
3.2 模型加速度响应
为研究立体交叉隧道受空间位置影响,从而导致地震波在围岩中传播特性的改变,对坡体内部交叉段及非交叉段的加速度响应进行分析。采用加速度放大系数来研究围岩的动力响应,PGA(peak ground acceleration)放大系数定义为各测点的实测加速度峰值与台面输入加速度峰值的比值。坡体内部交叉段及非交叉段的PGA放大系数结果如图11所示。
(a) 上跨隧道

(b) 非交叉段图11 坡体内部围岩的PGA放大系数Fig.11 PGA amplification factor of surrounding rock in slope
由图11可知,交叉段与非交叉段各测点的加速度响应表现出明显的规律性。随着输入地震波峰值的增大,非交叉段PA1~PA8各测点的PGA放大系数随之增大;交叉段除TA6测点外其余各测点的放大系数也随之增大。对于交叉段TA6测点,在输入地震波加速度峰值为0.4g~0.6g时,其加速度放大系数呈现出减小的趋势。叶帅华等[29]对黄土边坡大型振动台模型试验研究中也发现类似的规律,这是由于随着围岩内部累积损伤逐渐增大,消耗部分地震能量,使围岩的滤波效应更加明显,阻碍地震波在竖向的传播能力,因而明显削弱加速度放大效应。此外,由于加速度放大效应一般由围岩的自振频率与地震波的主频相近程度来确定,当频率接近时,放大效应越明显,反之放大效应越弱甚至响应会出现衰减[30]。
在靠近上跨隧道拱顶处,非交叉段(PA2及PA3测点)的PGA放大效应相较于交叉段(TA2及TA3测点)更为明显。而越靠近模型箱底部,交叉段处(TA5及TA6测点)的PGA放大效应出现突增,其PGA放大系数远远大于非交叉段。以交叉段TA6测点及非交叉段PA6为例进行说明,其在0.1g~0.6g地震波作用下PGA放大系数分别为2.47、2.16、2.97、3.35、4.30及0.74、1.15、1.21、1.36、1.94。分析其原因是由于上跨隧道及下穿隧道的存在,使交叉段的加速度响应出现空间耦合叠加效应,导致交叉段的加速度响应异常增大,因此交叉段可能会成为全线的薄弱区段。总体来看,由模型箱底部至坡顶其加速度放大效应基本都表现出增大→减小→增大→减小,出现两次峰值。但交叉段与非交叉段PGA放大效应的峰值出现位置不同,交叉段的加速度响应在靠近下穿隧道拱顶处(TA6)最为强烈,而非交叉段的加速度响应在靠近上跨隧道拱顶处(PA3)最为明显,同时TA6的地震响应也明显大于PA3处。这也与上述动应变在上跨隧道拱顶、仰拱及下穿隧道拱顶处响应较为强烈相吻合。由此也表明除交叉段薄弱环节外,上跨隧道拱顶处围岩对地震波的敏感性强,也应该成为抗震过程中需要重点关注的部位。
3.3 反应谱响应特性
在振动台模型试验中所监测数据一般是各测点信号的峰值或时程曲线,但地震波的频谱特征及其动力损伤机制并不能从原始监测数据中准确地表达出来。因此,有必要引入相关手段来分析地震波谱特性对隧道及围岩动力响应的影响。地震反应谱理论(位移谱、加速度谱、速度谱)考虑地震动与结构之间的动力关系及影响,并能表征结构的自振频率(周期),在评价结构动力响应过程中被广泛应用[31]。在动力反应谱分析中,模型测点处的围岩材料一般被视为刚体单元,这样所获得的动力响应谱能够反映隧道不同位置土体单元在给定地震波激励过程中的最大位移响应、速度响应和加速度响应随测点周期变化的规律,具有较大工程意义[32]。
地下结构在地震过程中主要受周围地层的影响,其破坏来自周围土体的变形。因此,隧道结构的地震响应更应关注围岩的变形特征。以0.1g(弱震)、0.4g(中震)及0.6g(强震)工况为例,并选取具有典型代表性的交叉段TA3-T7测点作为研究对象进行位移反应谱分析。需要说明的是,计算过程中按照工程中常用的5%阻尼比进行处理。不同加速度峰值El-Centro波作用下,各测点的位移反应谱如图12所示。
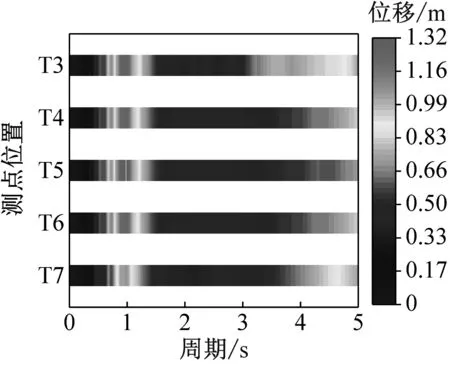
(a) 0.1g
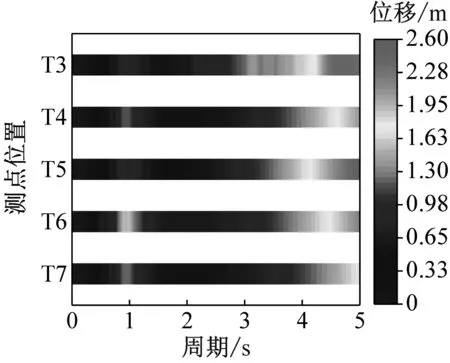
(b) 0.4g

(c) 0.6g图12 不同测点位移谱分布图Fig.12 Displacement response spectrum distribution of different measuring points
由图12可得,在不同地震荷载作用下交叉中心断面各测点位移反应谱分布规律具有明显的异同性。随着输入地震波幅值的增大,各测点位移反应谱也随之增大;同时也可以发现,除坡体内交叉段TA5测点外,其余各测点的反应谱特性曲线沿高程方向有明显的放大效应。分析产生这种现象的原因是隧道间地震波的折射和反射,在空间上会产生反应谱的叠加效应,导致交叉段位移谱振幅异常增大。
在0.1g地震波作用下,各测点位移谱幅值基本都小于1.3 cm,围岩变形位移较小,表明此时围岩及隧道并未产生明显的损伤和破坏。在0.4g地震波作用下,最大位移谱幅值出现在坡体内交叉段TA5测点,为2.55 cm,表明此时交叉段已产生损伤,局部围岩可能出现变形或产生裂缝。而在0.6g地震波作用下,最大位移谱幅值已达到6.47 cm,这也说明随着地震荷载的增大,围岩的内部累积损伤增大,地震能被逐渐消耗,围岩的刚度减小,模型已产生较大变形。以TA3测点为例,在0.1g、0.4g及0.6g地震波载荷下的位移反应谱幅值分别为1.29 cm、2.42 cm及6.47 cm,后者分别是前者的1.87倍及2.67倍;这表明在0.4g~0.6g加载阶段围岩的损伤速率大于0.1g~0.4g阶段,这可能是由于在后一加载过程围岩应力强度因子幅值增大至其断裂强度[33],围岩的承载力被明显削弱,致使模型处于失稳状态。
此外,随着输入地震波幅值的增大,各测点位移反应谱的卓越周期逐渐增大,即卓越频率减小。在0.1g地震波作用下,0.5~1.5 s短周期内具有显著的峰值特征,而在长周期内反应谱沿高程的放大作用较小;而在0.6g地震波作用时,在长周期3.0~5.0 s内位移反应谱沿高程具有明显的放大效应,而在短周期2.0 s以内,其位移反应谱的幅值基本已趋于0。表明随输入地震波幅值的增大,围岩的非线性特征明显增加,阻尼比增大而使围岩对于高频地震信号的滤波效应显著增加,即围岩对低频地震波产生明显的放大作用。
4 结 论
为了研究立体交叉隧道的地震动力响应,对隧道的动应变及围岩的加速度响应进行分析,并使用反应谱理论对坡体交叉段的位移谱进行了探讨,主要得到以下结论:
(1) 上跨隧道的轴向应变响应整体大于下穿隧道,说明由于上跨隧道的影响及围岩的挤密效应,减弱了地震波对于下穿隧道的冲击作用;此外,隧道拱顶处会产生应变的“叠加效应”,易成为隧道结构潜在的震害破坏区。
(2) 在地震波传递过程中,隧道不同位置处的能量损耗程度不同,从而导致结构的破坏具有一定的“滞后性”,上跨隧道可能会更早出现破坏且破坏也更为严重。因此,对于高烈度地震区的立体交叉隧道工程而言,上跨隧道应为抗震设计的重点关注对象。
(3) 加速度放大效应沿高程方向呈增大→减小→增大→减小的趋势,表现出明显的峰值特征;但交叉段与非交叉段加速度放大效应的峰值出现位置不同:非交叉段在靠近上跨隧道拱顶PA3测点处放大效应最为明显;而交叉段却出现在下穿隧道拱顶TA6测点处。
(4) 卓越周期随输入地震波幅值的增大而逐渐增大,即卓越频率逐渐减小;同时在不同幅值地震波作用下,峰值特征在不同周期内表现出较大差异:在弱震(0.1g)作用下,短周期0.5~1.5 s内位移反应谱具有显著的放大效应;而在强震(0.6g)作用下,长周期3.0~5.0 s内位移反应谱沿高程具有明显的放大效应。
由于空间立体交叉隧道的地震动力响应较为复杂,本文仅对斜交型立体隧道的动力响应进行了分析,所得结论需要更多试验的补充完善及数值模拟的验证。同时后续仍需对正交型立体隧道的动力响应及两种不同交叉形式隧道的异同性进行深入探讨。

