考虑桩基错动的深水张力腿平台动力响应研究

余 杨， 张晓铭， 李振眠， 周俊龙, 成司元， 崔宇朋， 余建星， 杨政龙

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.天津大学 天津市港口与海洋工程重点实验室，天津 300072;3.中国建筑第六工程局有限公司，天津 300171)

张力腿平台(tension leg platform,TLP)是顺应式平台的典型形式，常用于深水及超深水海洋油气开发[1]。作为海洋油气开发的关键基础设施，开展TLP的安全性研究具有重要的现实意义和实用价值。在TLP的运行过程中，由于地震、断层、滑坡和沉降等原因，张力腿下端的桩基可能发生错动，改变平台系统的动力特性，进而影响平台的正常作业，甚至导致张力腿断裂、平台倾覆等重大安全事故。特别地，针对我国南海海洋环境十分复杂恶劣，海底滑坡、地震等深水地质灾害频发[2]，严重影响该海域上平台结构的正常运行。因此，开展考虑桩基错动的深水张力腿平台动力响应研究能够为我国海洋平台装备设计与制造和南海海域深水油气开发工作提供指导。

到目前为止，世界上已建和在建的TLP共25座，主体结构形式主要有传统式TLP、海星式TLP、最小化深水海面设备结构和延伸式TLP[3]。TLP动力响应分析方法主要有频域分析和时域分析。频域分析将TLP近似为线性系统，求解高效，适用工程运用中大量工况的计算。而时域方法能够考虑了平台所有的非线性因素，提供更加准确的结果，但需要较高的计算成本[4]。Zeng等[5-6]论证了TLP在波浪作用下发生有限振幅运动时，所受惯性力、黏性力、浮力等载荷以及张力不仅与波浪有关，还与瞬时响应有关，是响应的非线性函数。徐万海等[7]将TLP参数化简化为非线性梁结构，通过理论计算该数学模型对TLP模型动力响应预测结果的影响。Chandrasekaran等[8]分析中等规则波下三角形TLP受到垂直地震力的影响，发现地震力使得平台偏移，系泊张力变得不平衡。Wang等[9]对地震和波浪激励下浮式结构非线性随机振动进行研究，计算了各种条件下结构的运动响应和系泊缆线中最大拉力的平均值。闫功伟等[10]则针对极端海况下的附加浮筒后的改良TLP平台建立多体耦合运动分析模型并在时域下求解。李焱等[11]则更关注畸形波对TLP平台的动力响应特性的影响。常爽等[12]则研究考虑畸形波影响的TLP平台的波浪力与畸形波聚焦位置对平台动力响应的影响。Jameel等[13]对TLP平台从极端到中等海况的运动和系泊线张力进行研究，提出解决TLP有限元非线性问题的程序。沈晓鹏[14]在浮式平台的基础上进一步开展了TLP平台非线性动力响应与疲劳研究得出完整的TLP的非线性六自由度运动方程，刘洋[15]又在这基础上对TLP平台的有限位移运动开展研究各种非线性因素对平台动力响应的研究。Yu等[16]对TLP局部失效时船体与筋腱的非线性耦合效应下的六自由度动力响应进行研究。Hao等[17]开展了系泊局部失效时张力腿平台的运动响应研究，评估系泊局部失效时平台结构的安全性。成司元等[18-19]对TLP平台局部失效的机理开展了进一步的研究。余建星等[20]同时针对TLP平台系泊局部失效下的抗连续失效能力提出了鲁棒性评估方法。Song等[21]通过实验研究新设计的增加系泊线的TLP性能与传统TLP性能的差异，并证实系泊线对提高系统性能的显著贡献。李磊等[22]更是针对TLP平台的涡激振动问题设计了一套锚泊方案，并进行深入研究。

本文考虑由于地震、断层、滑坡和沉降等引起的TLP桩基错动问题，分析其对TLP动力响应的影响，以期为浮式平台安全设计和减灾防灾提供设计参考。首先针对平台可能发生的大幅运动建立了TLP系统非线性耦合动力学方程，编程计算并与文献数据进行对比验证。然后，针对桩基错动的位置和数量设计了16种工况，计算得到基于南海流花油田一年一遇的设计工况的TLP动力响应结果。最后，以正常工况为基准，对比分析了不同桩基错动工况对TLP动力响应的影响情况。

1 理论模型

1.1 TLP动力学方程

如图1所示，取平台本体处于静平衡位置时的重心的空间位置为坐标原点，建立固定的坐标系(x,y,z)，另外取平台本体的重心建立随平台运动的随体坐标系(ξ,η,ζ)。在初始时刻，固定坐标系和随体坐标系重合。平台本体在波浪力和张力腿的共同作用下，会产生6个自由度方向的运动，分别是纵荡X1，横荡X2，垂荡X3，横摇X4，纵摇X5和首摇X6。

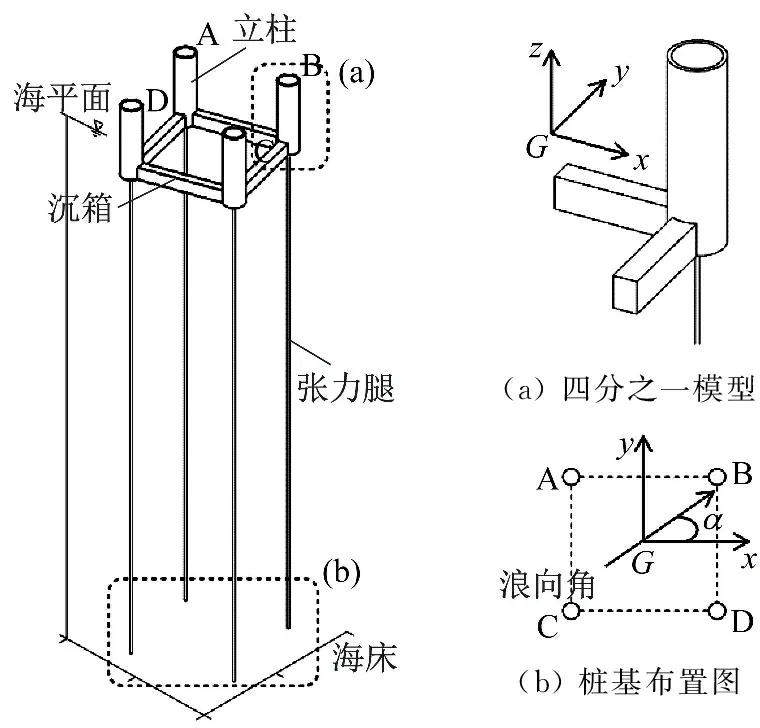
图1 TLP模型示意图Fig.1 Comparison and verification of six degree of freedom response of ISSC-TLP

考虑固体坐标系和随体坐标系的转换关系为

(1)

式中,A为3×3坐标转换矩阵，即

各元素如下

t11=cos(X5)cos(X6)，

t12=-cos(X5)sin(X6)，

t13=sin(X5)，

t21=sin(X4)sin(X5)cos(X6)+cos(X4)sin(X6)，

t22=-sin(X4)sin(X5)sin(X6)+cos(X4)cos(X6)，

t23=-sin(X4)cos(X5)，

t31=-cos(X4)sin(X5)cos(X6)+sin(X4)sin(X6)，

t32=cos(X4)sin(X5)sin(X6)+sin(X4)cos(X6),

t33=cos(X4)cos(X5)。

建立张力腿平台本体六自由度方向的运动方程如下

(2)

式中:M为平台本体质量;I1、I2、I3为对应方向转动惯量;右端是单个圆柱在运动中受到的载荷，包括了F-K力,惯性力，辐射力以及浮力和张力腿的拉力。横摇、纵摇和首摇方向的角速度和角加速度计算公式如下

1.2 外载荷

根据改进莫里森方程，水中单位长度微元体受到的水动力为

(3)

标记平台本体的四个立柱和四个沉箱为k(k=1,2,…,8)，分别沿其浸没长度k积分可得波浪力和力矩为

(4)

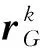
(5)

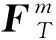
(6)

1.3 时域数值计算方法

根据以上推导过程，综合式(1)～(6)可得到张力腿平台系统耦合动力学方程，经过整理可降阶写为

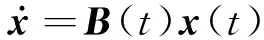
(7)

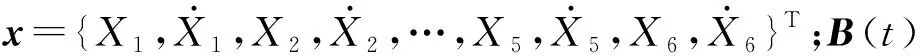
2 计算参数及数值验证

2.1 计算参数

本文选用传统式TLP(ISSC-TLP)作为研究对象，该平台由一个甲板、四个立柱、四个沉箱和四个张力腿组成，相关参数如表1所示。

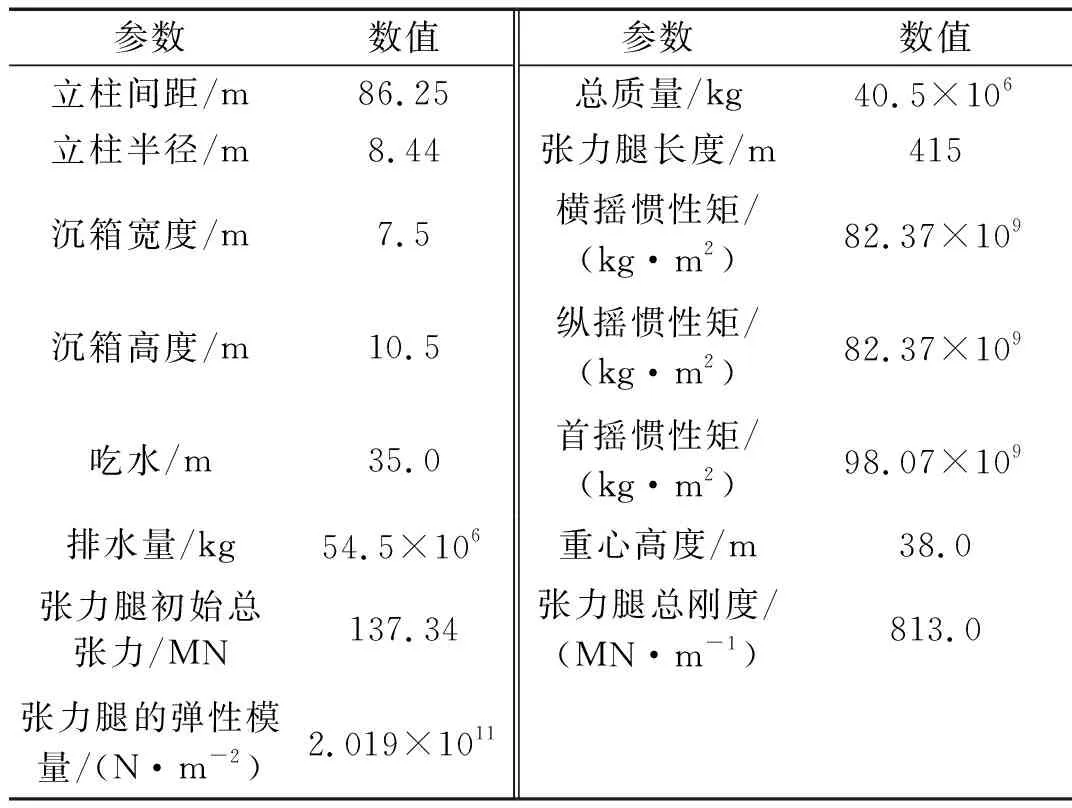
表1 ISSC-TLP计算模型参数Tab.1 Issc-TLP calculation model parameters

本文采用海浪谱描述海面，选用南海404.69 m水深的流花油田一年一遇海况数据作为设计工况，如表2所示。对于已知JONSWAP波浪谱，采用随机相位法[1]对合成海况进行模拟。

表2 波浪数据Tab.2 Wave data

针对在初始状态时不同桩基下降0.1 m的情况，对图1中A、B、C和D四个张力腿桩基进行排列组合，得到16种计算工况，如表3所示。其中，C1为无桩基下沉工况，C2～C5为单个桩基下沉工况，C6～C11为两个桩基下沉工况，C12～C15为三个桩基下沉工况，C16为桩基全部下沉工况。

表3 设计工况Tab.3 Design condition

2.2 TLP算例验证

为验证算例的正确性，与Zeng等的计算结果进行对比，计算了在文献工况(波高8.0 m，周期14.0 s，浪向角22.5°)下ISSC-TLP平台本体的六自由度运动响应。Zeng等也考虑了平台本体有限位移、瞬时湿表面、瞬时位置、六自由度运动耦合、自由表面效应和黏性力等非线性因素的影响。由图2可知，本文计算结果与前人结果吻合良好，本文理论模型和计算程序的正确可靠。

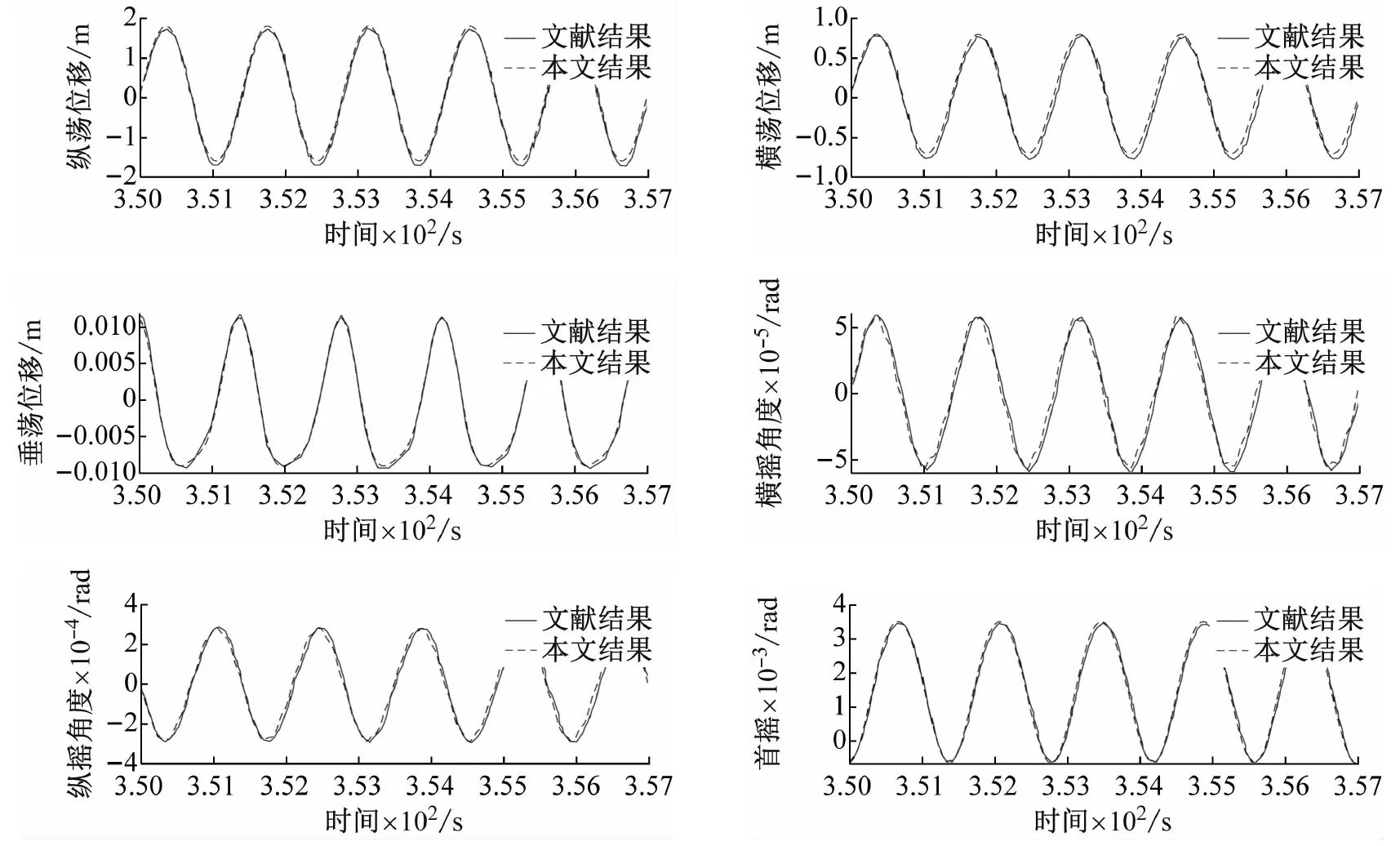
图2 ISSC-TLP六自由度响应对比验证Fig.2 Comparison and verification of six degree of freedom response of ISSC-TLP

3 动力响应分析

3.1 动力响应分析

一般地，张力腿平台的纵荡方向沿着主浪向布置，以避免平台剧烈的运动。因此，本文根据表2所得模拟数据计算了浪向角为0°时，C1～C16工况下平台本体六自由度运动响应和张力腿的张力响应，具体方向如图1所示。限于篇幅，此处只展示C1、C2、C6、C12和C16平台本体六自由度位移(角度)响应、速度(角速度)响应和四根张力腿的张力响应的时历曲线。选取响应数据的波动区间比较稳定的时间窗口5 000～6 000 s进行分析。

图3为平台本体六自由度位移(角度)响应和速度(角速度)响应时历曲线。图中颜色较难分辨的位置为两条或多条曲线重合导致，较易分辨的位置则代表曲线有较大区别。由图3(a)可知，对于C2、C6和C12工况来说，张力腿桩基之间相对的错动会改变平台原有的对称特性，导致0°浪向角下平台在横荡、横摇和首摇方向上产生位移(角度)响应。具体的，横荡方向为从几乎无波动到最大幅值约为0.05 m的负偏移、明显波动，横摇方向为从几乎无波动到最大幅值约为0.000 8 rad的正偏移、不明显波动，首摇方向为明显波动。另外，垂荡方向为负偏移，且随着下称桩基数量增多，平台下沉越明显，从几乎无波动到最大幅值约为0.06 m。纵摇方向上不同工况变化情况有所差异：C2工况发生正偏移，C6工况偏移不明显，C12工况发生负偏移。而C16工况属于桩腿之间无相对错动整体在垂荡方向上发生位移，并未破坏原先的对称特性，因此只在垂荡方向上产生无明显波动、负偏移的位移响应，从几乎无波动到最大幅值约为0.075 m，其他方向则与C1工况无区别。由图3(b)可知，速度与位移是始终相对应的，因此若发生的位移偏移为无波动的位移响应则产生的速度响应无波动变化只有幅值产生变化，若发生的位移偏移为明显波动的位移响应则产生的速度响应有明显的响应变化。因此平台相应地在横荡、横摇和首摇方向上产生明显的速度(角速度)响应，在垂荡方向上有小幅度的偏移速度响应，而纵荡和纵摇方向上无明显偏移和波动差异。

图3 ISSC-TLP六自由度响应Fig.3 ISSC-TLP six degree of freedom response

图4为四根张力腿的张力响应时历曲线。图中颜色较难分辨的位置为两条或多条曲线重合导致，较易分辨的位置则代表曲线有较大区别。由图4可知，张力腿桩基错动会对张力腿拉力响应产生明显影响。C2工况对应张力腿A的桩基下沉，张力腿A的张力均值明显增大，从均值约3.5×104kN增长至均值约4.5×104kN，张力腿B的张力则变化不明显，张力腿C的张力均值小幅增大，从均值约3.5×104kN增长至均值约3.75×104kN，张力腿D的张力均值小幅减小，从均值约3.5×104kN减小至均值约3.2×104kN。C6工况对应张力腿A和B的桩基下沉，张力腿A和B的张力均值明显增大，张力腿A从均值约3.5×104kN增长至均值约4.2×104kN，张力腿B从均值约3.5×104kN增长至均值约4.8×104kN，张力腿C和D的张力则变化不明显。C12工况对应张力腿A、B和C的桩基下沉，张力腿A、B和C的张力均值明显增大，张力腿A从均值约3.5×104kN增长至均值约4.5×104kN，张力腿B从均值约3.5×104kN增长至均值约4.2×104kN，张力腿C从均值约3.5×104kN增长至均值约4.5×104kN，张力腿D的张力则几乎无变化。C16工况对应张力腿A、B、C和D的桩基整体，对应张力皆增大，张力腿A从均值约3.5×104kN增长至均值约4.2×104kN，张力腿B从均值约3.5×104kN增长至均值约5.5×104kN，张力腿C从均值约3.5×104kN增长至均值约4.2×104kN，张力腿D从均值约3.5×104kN增长至均值约4.2×104kN。可见，张力腿桩基下沉对对应张力腿张力影响最大，对角布置的张力腿影响次之，其他的张力腿影响最小。

图4 张力腿拉力响应Fig.4 Tension response of tension leg

3.2 桩基错动的影响

图5为16个工况下平台六自由度位移(角度)响应的最大绝对值和标准差比较。从最大绝对值上看，纵荡位移受到桩基下沉的位置和数量的影响较小，整体变化幅值小于20%，其他自由度则容易出现非常大的恶化，这也源于在0°浪向角下，其他自由度的响应本身较小，因此变化率较大。其中垂荡和纵摇产生的位移或角度响应变化基本都在5倍以内，但是横荡、横摇和首摇产生较大变化。横荡产生从几乎为0达到10-2数量级的位移响应，横摇产生从几乎为0达到10-4数量级的角度响应，首摇产生从几乎为0达到10-3数量级的角度响应。C2～C6和C11～C15的桩基下沉破坏了平台的对称性，横荡、横摇和首摇均出现了位移或者角度响应，。平台不再具有对称性时，横荡位移最大绝对值和标准差相对于纵荡位移比较小。C2～C5和C12～C15工况中横摇角度最大绝对值和标准差小于纵摇角度，而C6和C11工况中则较大。对于首摇角度，C6和C11工况中出现较大响应和明显波动，其余工况则小于纵摇角度。C7～C10和C16工况中下沉的桩基与平台保持有相同的对称性，横荡、横摇和首摇未出现位移或者角度响应。无论何种工况，桩基下沉均会导致垂荡位移的较大变化。对于张力腿平台，垂荡位移影响张力腿受力和生产立管的运行，因此由于桩基下沉而导致垂荡位移的恶化应引起足够的重视。另一方面，从标准差上看，去除横荡、横摇和首摇自由度，其他自由度的标准差变化不大，可以认为由于桩基下沉不会明显加剧平台运动响应波动。

(a) 最大绝对值

(b) 标准差图5 平台六自由度位移(角度)响应的最大绝对值和标准差比较Fig.5 Comparison of maximum absolute value and standard deviation of six degree of freedom displacement (angle) response of platform

图6为16个工况下平台六自由度速度(角速度)响应的最大绝对值和标准差比较。横荡、横摇和首摇产生较大变化，横荡产生从0达到10-3数量级的速度响应，横摇产生从0达到10-7数量级的角速度响应，首摇产生从0达到10-4数量级的角速度响应，除去横荡、横摇和首摇，可以看出桩基下沉的位置和数量对平台各个自由度速度或角速度影响非常小。而对于横荡速度最大绝对值及其标准差，相比于纵荡自由度是非常小。横摇角速度最大绝对值和标准差相对于纵摇自由度比较小，而首摇自由度约为纵摇自由度的2倍～3倍。可见，对称性破坏对首摇影响非常明显。

(a) 最大绝对值

(b) 标准差图6 平台六自由度速度(角速度)的最大绝对值和标准差比较Fig.6 Comparison of maximum absolute value and standard deviation of platform six degree of freedom velocity (angular velocity)

图7为四根张力腿的张力最大绝对值和标准差比较。如图7(a)所示，张力腿张力出现偏大增幅的工况有C2、C4、C5和C14；大增幅的有C3、C6、C7、C9和C12；非常大增幅的有C10、C13、C15和C16；只有C8和C11的增幅是中等的。对于张力腿张力的标准差，增幅都是非常小。也就是说，张力的波动剧烈程度变化不明显。对于ISSC-TLP，其张力腿如果为X70材质，拉断应力为570 MPa，换算成拉力约为67 000 kN。本文考虑桩基下沉0.1 m的情况，C10、C13、C15和C16的张力腿拉力达到了57 000 kN以上，约为断裂拉力的85%。如果桩基下沉更大的位移或者更剧烈的海况，张力腿拉力将更大，出现拉断的危险。

(a) 最大绝对值

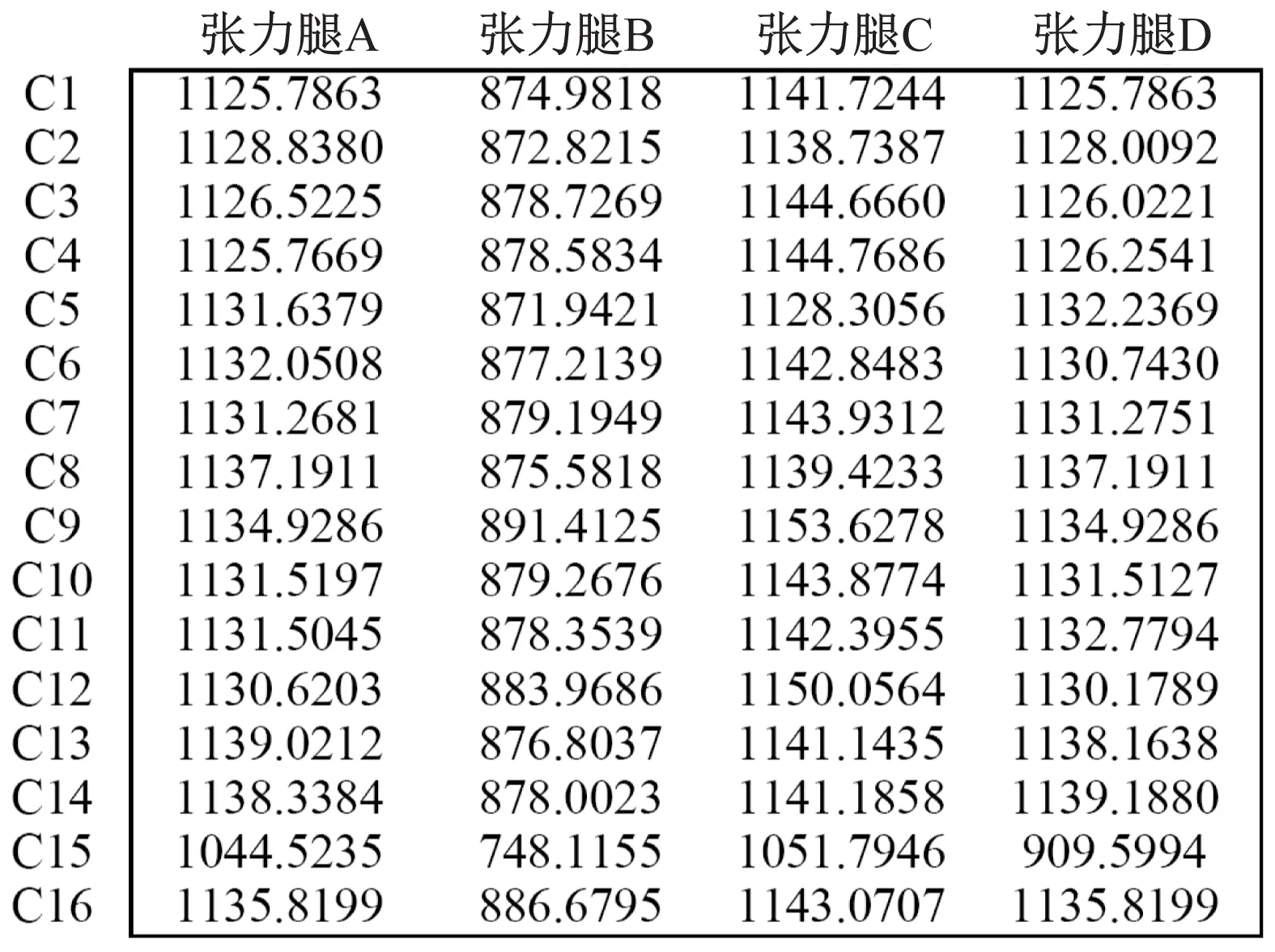
(b) 标准差图7 张力腿拉力的最大绝对值和标准差比较Fig.7 Comparison of maximum absolute value and standard deviation of tension leg tension

4 结 论

本文针对深水张力腿平台，考虑由于地震、断层、滑坡和沉降等引起的桩基错动问题，建立考虑平台本体有限位移、六自由度运动耦合、瞬时位置和瞬时湿表面、自由表面效应等非线性因素的张力腿平台系统的耦合动力学方程，计算得到基于南海流花油田一年一遇的设计工况下16种工况的平台动力响应时间历程。通过研究得到以下结论：

(1) 桩基下沉对平台的六自由度响应幅值产生明显影响，但不会明显加剧平台本体各个自由度运动响应的波动。当桩基下沉位置与平台本体不具有相同对称性时，平台系统原有的对称性会被破坏，主浪向下本体的横荡、横摇和首摇均出现了位移或者角度响应。无论下沉桩基的数量和位置，平台本体的垂荡位移均会发生较大恶化，严重影响张力腿受力和生产立管的运行，应给予足够的重视。

(2) 桩基下沉对张力腿张力幅值产生明显的影响，但不会明显加剧张力腿张力响应的波动。。计算的一年一遇海况下15个桩基错动工况中，2个工况张力腿张力增幅小于30%，4个工况增幅30%～40%，5个工况增幅40%～50%，4个工况增幅大于50%。张力腿最大张力达到57 000 kN，约为断裂张力的85%。如果桩基下沉更大的位移或者更剧烈的海况，张力腿拉力将更大，出现拉断的危险。