基于PSO-FAHP模型的办公座椅需求评价体系的应用分析

彭鑫月 尹志远,2 陶 涛* 陈星艳 袁 园,3 宋 玲

（1.中南林业科技大学，湖南 长沙 410014；2.圣奥科技股份有限公司，浙江 杭州 310000；3.湖南科技职业学院，湖南 长沙 410004）

随着办公座椅行业的不断发展，行业内竞争也日趋激烈，同质化产品层出不穷，而人们对于办公座椅的需求形式在不断变化。座椅的设计通常充满主观性和不确定性，设计者往往会依据个人爱好突出某一方面的性能，却忽略了其他方面的性能[1]。针对以上情况，一些专家和学者对办公座椅产品的设计评价体系进行了一系列的探索和研究[2-13]。

层次分析法（AHP）作为一种定性分析和定量分析相结合的决策分析方法，具有简单、灵活等特点，被广泛地应用于多目标、多准则、非结构化的复杂决策问题[14]。由于层次分析法受主观意识影响严重，得到的结果不够精确，因而相关学者提出了模糊层次分析法（FAHP），并将模糊数学引用于其中进行处理，使分析结果更令人信服。FAHP具有两种形式，一种基于模糊数[14]，另一种则基于模糊一致矩阵[15]。由于后者更符合人们的思维惯性，易于编程实现，因而本文采用基于模糊一致矩阵的FAHP方法进行研究。虽然FAHP对AHP进行了改进[16-17]，但在运算中，依然存在模糊判断矩阵的一致性检验过程繁琐、计算工作量大、修正困难等问题。且在实践应用过程中无统一的修正标准，缺乏相关科学理论和方法的指导。采用智能优化算法对其改进，通过完全一致性模糊矩阵的定义和性质进行约束求解，不仅可以获得理想的一致性结果，还能大大减少计算量，使得计算出的最优解具有可行性。目前，满足要求的智能优化算法有粒子群优化算法、遗传算法、神经网络算法、蚁群算法等。

粒子群优化算法（Particle Swarm Optimization，简称PSO）起源于对鸟类捕食行为的模拟[18]，是由Eberhart博士与Kennedy博士发明的一种新型全局优化进化算法[19]。与其他算法相比较，PSO算法收敛速度更快，使用方便且算法易编程实现，因此本文拟在FAHP法中引用PSO，构建PSO-FAHP模型，并将其应用于权重值的计算与优化，最后通过模糊综合评价法对4款热销办公座椅的设计案例进行评价分析，得出最佳设计方案，验证了模型的可行性，使综合评价的结果更为科学可靠。

1 基于PSO-FAHP模型的建立与求解

1.1 粒子群算法

在PSO算法中，将优化问题求解比作搜索空间内的一只鸟，称其为“粒子”，所有的粒子(i)都有一个由优化函数确定的适应度值(Fitness Value),以及速度(V)和位置(Present)，来确定其飞行方向与距离[19]。粒子群初始化为一群随机粒子，能够追随当前的最优粒子在解空间中不断搜索，并且在整个解空间中进行循环迭代过程，从而使群体中的每个个体(粒子)的速度和位置得以修正，直到算法结束。在PSO中，不存在交叉和变异的运算，粒子群中的粒子在迭代过程中跟随解空间中的最优个体进行搜索，最终找到最优解。

假定在一个D维目标搜索空间中有N个粒子构成一个群体，其中，第i个粒子代表D维空间向量Xi=(Xi1，Xi2，…，Xid)，i=1，2，…，N。第i个粒子的飞行速度亦是D维的向量，记为Vi=(Vi1，Vi2，…，Vid)，i=1，2，…，N。第i个粒子至今为止所搜寻到的最优位置称为个体极值(Pbest)，记为Pbest=(Pi1，Pi2，…，Pid)，i=1，2，…，N。整个粒子群至今为止所搜寻到的最优位置称为全局极值(gbest)，记为gbest=(Pg1,Pg2,…,Pgd)。当搜索到这两个最优值时，粒子更新速度及位置的计算公式为:

式中：Vid为粒子速度；W为惯性权重值，Vid∈[-Vmax,Vmax]，Vmax为常数，被用户设置用于约束粒子的速度；t代表进化过程的迭代次数；C1和C2为学习因子，又称作加速常数，为非负常数，合适的C1和C2可以加快收敛且不限于局部最优；r1和r2作为随机数取值介于(0，1)之间。本文采用了标准粒子群优化算法中的参数设置，即惯性权重W=0.8，学习因子C1=2，C2=2。

1.2 马斯洛需求层次理论

马斯洛需求层次理论是由美国著名社会心理学家亚伯拉罕·马斯洛提出来的一种激励心理学理论[20]。该理论将人类需求结构归纳为五个层次，依次为生理需求、安全需求、社交需求、尊重需求和自我实现需求，呈从低级到高级、从基本到高级的金字塔结构[21]，组成了不同的等级或水平，能激发并指导个体行为。在马斯洛看来，当一定水平的需要得到一定程度的满足后，对较高层次的追求将是推动个体行为的一种力量，而人类需要通过满足各层次的需求以达到自我实现。该理论与人类需求发展的普遍规律和产品设计需求发展的一般规律相符合。因此，本文以马斯洛需求层次理论为基础，结合办公座椅产品的设计标准，提出办公座椅需求。

1.3 PSO-FAHP模型构建

结合模糊层次分析法和粒子群算法的基本理论、计算方法以及近年来的应用和改进情况，提出如图1所示的计算步骤。

图1 PSO-FAHP模型Fig.1 The PSO-FAHP model

构建PSO-FAHP模型的过程如下：

1）建立评价指标体系。 假定评价指标体系自上而下指标层有三层，第一层为目标层，即模型的最高层次，只包含一个元素，记作P；第二层为准则层，记作B；第三层为子准则层。通常用B={b1,b2,b3,…,bn}表示因素集中的各元素，其中各元素的子集表示为Bi={bi1,bi2,bi3……bin}，i=1,2,3,…,n。

2）构造模糊互补判断矩阵。在模糊层次分析中通过两个因素之间的对比判断，用一个因素对另一个因素的重要性来定量表示，通常使用如表1的0.1～0.9标度法给予数量标度。

表1 0.1～0.9 标度法及其含义Tab.1 0.1～0.9 scale method and its meaning

Pii=0.5 表示元素与自己相比同样重要；若Pij∈[0.1,0.5]，则表示元素bj比bi重要；若Pij∈[0.5,0.9]，则表示元素bi比bj重要；根据上面的数字标度，元素b1,b2,…，bn之间相互进行比较，则得到模糊互补判断矩阵：

满足0 ≤Pij≤1，Pij+Pij=1，i，j= 1，2，3，…，n。

3）PSO算法求解优化模型并进行一致性检验及修正。根据模糊判断矩阵的定义，若P为模糊一致判断矩阵，具有完全一致性，则其具有以下性质：

(1)模 糊 互 补 矩 阵P=(Pij)n×n的 单 位 性：Pij=0.5，i=1,2,3,…，n；

(2)模糊互补矩阵P=(Pij)n×n的互补性：Pij=1-Pij；

(3)模糊互补矩阵P=(Pij)n×n的一致性条件：Pij=Pik-Pjk+0.5；

(4)模糊互补矩阵P=(Pij)n×n是模糊一致矩阵的充要条件为Pij=0.5+b(wi-wj)。

其中，性质③是性质①和性质②的充分条件，表明相互关系能够定量传递。i，j= 1，2 ，…，n；wi(i= 1，2 ，…，n)是每个元素的权重值，wi-wj代表矩阵第i行与第j行的权重之差；b是衡量两个元素重要性差异的单位，取值范围为b≥b取值越小，说明决策者对各元素之间重要性的差异重视度越高；b取值越大，说明决策者不是非常重视各元素之间重要性的差异[22]。

若模糊矩阵满足Pij=0.5+b(wi-wj)，模糊互补矩阵具有完全一致性，则有

为适应不同的复杂系统，FAHP只要求模糊判断矩阵P具有令人满意的一致性。然而，在实际问题的复杂性、人们主观意识不同等多种因素影响下，通常模糊判断矩阵P并不具有完全一致性，这种特性在实际应用中客观存在，并且不可能彻底消除[23]。若P不具有满意的一致性，则需要进行修正。本文利用PSO算法对模糊判断矩阵P进行一致性检验及修正。设P经过修正后的模糊判断矩阵是Y=(yij)n×n，那么其所对应的各评价指标权重仍记作wi(i=1，2，3，…，n)，且满足：wi＞0，且，则称下列公式取得最小值的Y矩阵为P的最优一致性模糊判断矩阵。

式中：CIF(n)为一致性指标函数(Consistent Index Function)；由模糊互补矩阵P=(Pij)n×n是模糊一致矩阵的充要条件为任意指定行和其他各行对应元素之差等于某一个常数[15]，这是模糊判断矩阵的加性一致性原理[24]，即模糊判断矩阵Y的加性一致性。因此，以不失一般性，假定对原始判断矩阵P=(Pij)n×n中的第一行元素把握最大，那么修正后的判断矩阵Y的第一行元素不需要变化，即表示Zij的均值，可以Zij的标准进行一致性约束[24]。

CIF(n)值越小，模糊判断矩阵P的一致性就越高。CIF(n)值是全局范围的最优值，当最优值小于0.1 时，得出所构造判断矩阵P具有令人满意的一致性；当全局最小值CIF(n)=0 时，则模糊判断矩阵P具有完全一致性且Y=P可知，该全局最小值是唯一的[25]。

运用MATLAB数学软件编程，实现PSO算法求解公式(3)。

PSO算法具体求解过程如下：

(1)初始化粒子群包括n个粒子以及每个粒子所处的位置与速度；

(2)计算每个粒子的适应度值；

(3)对比各个粒子的适应度值与个体极值，若适应度值优于个体极值，则以适应度值替换个体极值；

(4)对比各个粒子的适应度值和全局极值，若适应度值优于个体极值，则以适应度值替换全局极值；

(5)按照公式(1)(2)更新粒子的速度和位置；

(6)如果达到结束条件(误差足够好或达到最大循环次数)，则可输出结果，否则，回到步骤(2)。

2 PSO-FAHP模型在办公座椅设计方案评价中的应用

2.1 构建办公座椅评价体系

通过查阅大量文献资料、卖场调研、调查问卷、在线用户评论分析及到企业实习了解办公座椅全品类后，根据马斯洛需求层次理论，构建评价体系层次分析模型。调查问卷对象包括5位设计专家、5位产品经理、5位研发经理、5位产品设计师及200位办公人员，在收集完办公座椅产品用户的需求后，运用KJ法进行数据归纳，从而提出办公座椅的评价体系，如图2所示。

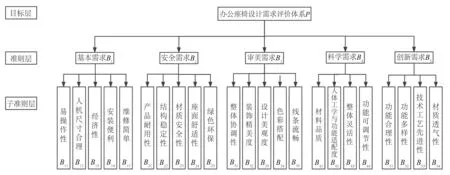
图2 办公座椅评价体系Fig.2 Office seating needs assessment system

2.2 建立模糊判断矩阵并确定权重

为阐明基于粒子群算法的模糊层次分析法在办公座椅产品设计方案选择中的实际应用，以热销的4款办公座椅（图3）为例，邀请企业负责人3人、行业专家5人、办公座椅研发经理10人、产品经理10人、设计师5人、销售人员6人和潜在消费者15人，共54人作为调研对象，其中女性28人，男性26人。根据模糊判断矩阵，调研对象对办公座椅设计需求评价指标进行两两比较并打分。将数据输入到MATLAB数学软件中并求解，根据PSO-FAHP模型，经粒子群优化算法（PSO）一致性检验及修正后，计算出每个层次下的评价指标权重值，得到各指标权重结果为Wg= (0.213 5 0.302 9 0.157 3 0.196 7 0.129 6)，见表2。同理，可计算出子准则层的指标权重值为：

图3 办公座椅产品设计案例Fig.3 Example of office seating product design

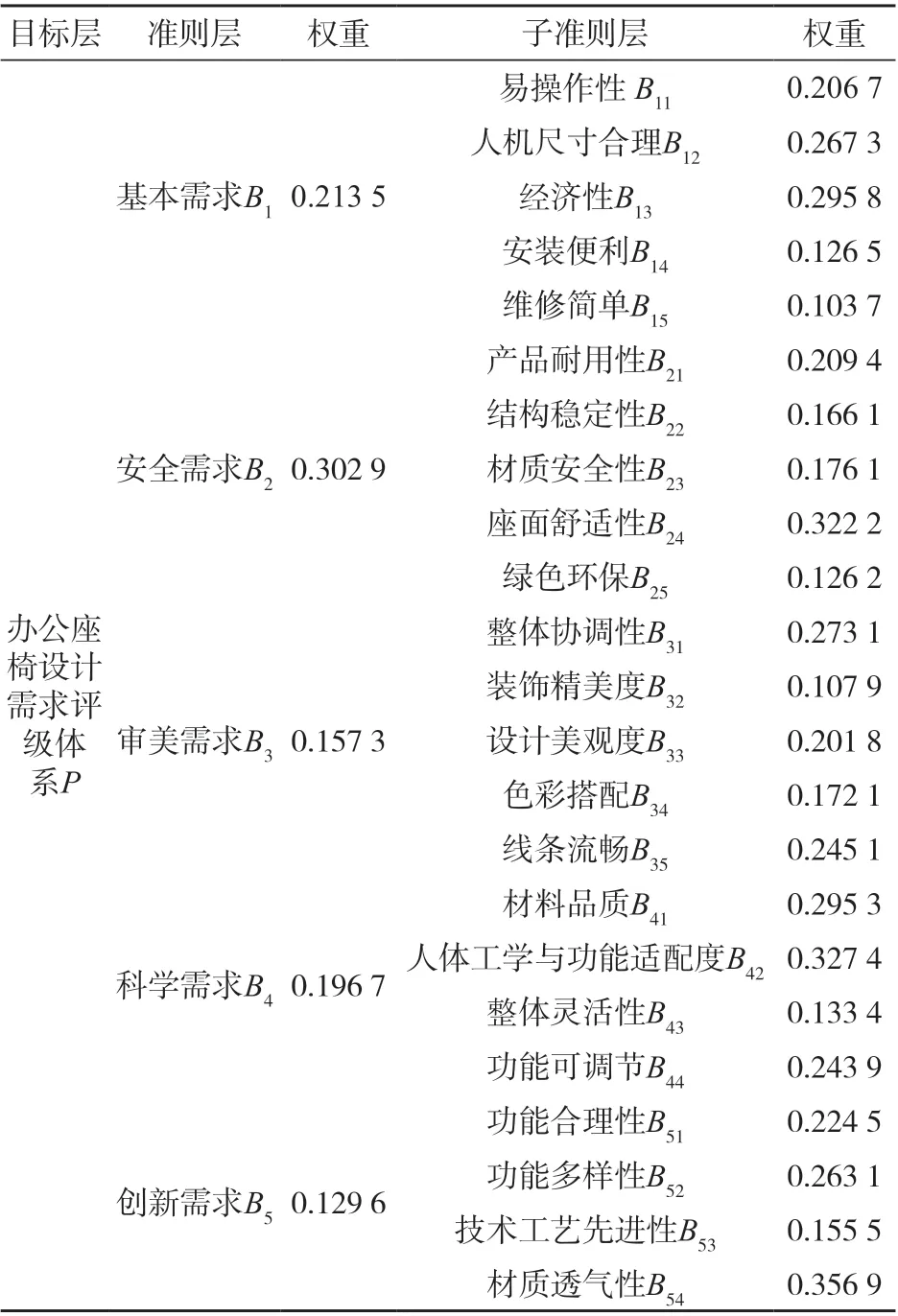
表2 各指标权重计算结果Tab.2 Results of the calculation of the weight of each indicator

2.3 模糊综合评价计算

根据评价指标体系权重值，结合上述办公座椅产品设计实例进行模糊综合评价[26]。为确保计算的客观性，需要对评价指标的评价结果进行量化处理。根据构建的层次需求评价指标，邀请10位行业内的专家对其各个准则层中的每一项评价指标进行评分，评价标准如表3所示。评价等级分为五个等级，分别为：优秀、良好、中等、劣、差，并规定各等级赋值，赋值向量依次为E=(90 80 70 60 50)T。

表3 评价等级及标准Tab.3 Grading levels and criteria

在计算隶属度时应遵循底层有限的原则，即从三级指标开始。以办公座椅产品设计A为例，各位专家分别对设计案例A进行打分，如评价指标B11收到6 次优的评价等级就记作0.6，以此类推，得到设计案例A对基本需求指标的评价结果，如表4 所示。

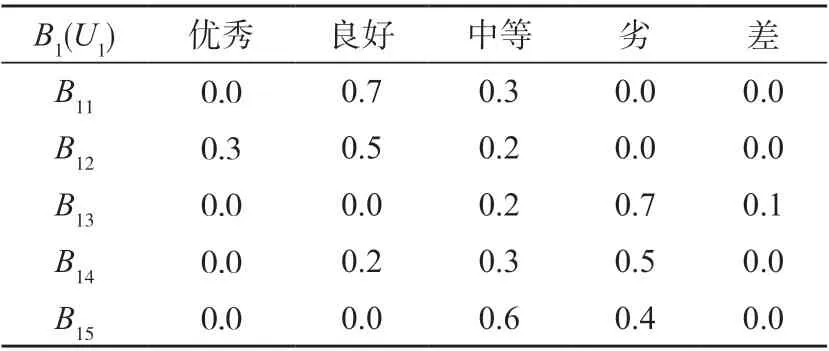
表4 设计案例A对基本需求指标的评价结果Tab.4 Results of the evaluation of basic needs indicators in Design Case A

在表4 中，评价矩阵U1表示准则层B1中对各个指标进行评价的结果。同理可得到U2=安全需求B2，U3=审美需求B3，U4=科学需求B4，U5=创新需求B5的模糊综合评价矩阵。

计算准则层对设计案例A的评价结果权重，计算方法为Qn=Wn×Un，计算结果如下：

基于计算结果，构建二级综合评价矩阵：

依照评价矩阵，把结果换算成百分制：

W=WgQ=（0.364 2 0.342 1 0.213 8 0.078 2 0.001 7）

设计案例A 最终得分=(0.364 2 0.342 1 0.213 8 0.078 2 0.001 7)(90 80 70 60 50)T= 79.889。

按此流程和方法对剩余3 个设计案例进行评价，得出各案例最终得分，分别如下：

设计案例B 最终得分 =(0.305 3 0.354 6 0.231 8 0.105 6 0.002 7)(90 80 70 60 50)T=78.542；

设计案例C 最终得分 =(0.226 4 0.298 0 0.308 2 0.143 6 0.052 0)(90 80 70 60 50)T=77.006；

设计案例D 最终得分 =(0.296 5 0.334 9 0.265 4 0.094 3 0.008 9)(90 80 70 60 50)T=78.158。

最终得分排序为设计案例A＆gt;设计案例B＆gt;设计案例D＆gt;设计案例C，由此可以确定设计方案A是最为符合人们实际需求的办公座椅产品。

3 结论

1）本文构建了办公座椅需求评价指标体系，运用模糊层次分析法和粒子群算法相结合的研究方法，构建PSO-FAHP模型并运用PSO算法对模糊判断矩阵进行一致性检验及修正，计算出各级评价指标权重，实现了对评价指标的量化处理。

2）以热销的4 款办公座椅设计为案例进行实例论证，根据模糊综合评价法对设计案例进行准确评价分析，得出最优方案。经验证，优选出的产品满足消费者的实际需求，证明了模型的可行性。

3）综合来看，运用智能算法改进层次分析法，能够大大节省计算量，使得评价结果更加科学合理，能更好地解决模糊、难量化以及各种不确定的问题，使方案的选择更为全面、客观、真实。