基于改进粒子群算法林产工业供应链网络研究

田昕加 王姝雅 赵 凤

（东北林业大学经济管理学院，黑龙江 哈尔滨 150006）

供应链管理除了包含商品、服务和信息从供应商到最终客户的转移，还能不断改善供应链绩效，并在此系统化过程中，为客户和供应链的可持续发展寻求价值[1]。可持续供应链管理是供应链管理的关键内容之一，以同时实现可持续发展三个维度（经济、环境和社会）为目标[2]，对企业物质资源、信息流、资金流进行管理，并协调各供应链公司[3]。随着我国经济社会发展进入新时代，社会主要矛盾发生变化，经济发展也由高速增长阶段转向高质量发展阶段，各大公司都逐渐意识到，可持续的做法可能更加经济，因其可以提高各利益相关者，如政府监管者、消费者、非政府组织、媒体等的满意度，创造新的收入[4]。

可持续供应链管理作为企业运营管理的重要方法，只有通过精心而合理的供应链网络设计与优化才有可能实现[5]。同时，为实现可持续，将回收产品等逆向物流处理对象考虑在内形成供应链闭环显得尤为重要[6]。因此，当前企业需要更加重视闭环可持续供应链网络的设计与优化，以应对日益激烈的竞争环境、更加严格的政府法规，进而实现可持续的高质量发展[7-8]。

在传统供应链网络基础上，学者们对各种不同行业的闭环可持续供应链网络进行了建模[9-12]。研究表明，对不同行业应建立具有不同特征的模型。为有效求解多目标网络模型问题，学者们对各种智能算法进行了研究[13-16]。随着算例规模扩大，模型计算复杂性相应提高，对求解方法要求也更为苛刻。因此，在确定求解算法时应谨慎处理模型参数并设计选择适应性更高的启发式算法。

总体而言，闭环可持续供应链领域的研究仍有待完善。已有闭环可持续供应链网络研究中虽考虑到对特定行业或产品进行案例研究并为其提出模型，但目前很少针对林产工业特点或其产品闭环可持续供应链做出相关研究。然而，林产工业在许多地区的社会和经济发展中发挥着重要作用[17]。如何增加林产工业相关企业的经济、环境、社会效益，是地区发展中的重要议题[18]。因此，有必要对林产工业或其产品的闭环可持续供应链网络模型进行研究，并选择设计优良的智能算法求解模型，以期为行业管理者提供更有价值、更个性化的参考意见。

1 可持续供应链网络模型

以林产工业中造纸及纸制品制造业为例，通过设计包含可持续发展的经济、环境和社会三方面的多目标数学规划模型，研究林产工业的可持续性闭环供应链管理。根据我国造纸供应链的实际情况，木材资源向纸产品流通转化主要有两条主线[19]。基于此，本文设计的纸制品闭环供应链网络结构如图1 所示。

图1 闭环供应链网络结构示意图Fig.1 Schematic diagram of closed-loop supply chain network structure

1.1 参数

在定义目标函数和约束条件之前，介绍模型所使用参数和决策变量。具体符号及含义如表1和表2所示。

表1 参数设置Tab.1 Parameters of mathematical model

（续表1）

表2 决策变量Tab.2 Decision variables of mathematical model

1.2 目标函数

模型包括三个目标函数，即经济目标、环境目标和社会目标。

经济目标：

经济目标由成本最小化式（1）得到，共由11 项构成。1～4 项分别为原材料成本、产品回收成本、运输成本、库存成本；第5～8 项为劳动力成本，其中第5 项为固定劳动力成本，其余3 项分别对应实体、技术和运输中劳动力可变成本；第9～11 项为投资成本，包含对实体、技术和运输的资金投入，其中由于模型规划期限为一年，考虑资金时间价值，所以利用将总投资转化为年度投资。

环境目标：

环境目标由纸制品生产过程碳排放水资源消耗最小化得到。环境目标函数涉及到两个不同层面，因此在式（2）中对其进行归一化处理，并表示为归一化值乘以其给定权重的公式。式Zwater计算了不同生产技术水消耗的影响；式计算了纸制品生产过程中采用不同技术、运输过程以及仓库使用过程的CO2排放。管理者还可以根据企业发展目标调整WW、WG权重的值。

社会目标：

社会目标由式（5）中定义的社会指标获得，主要是用创造的工作机会数量来衡量。第1 项反映的是加工厂和仓库所需的最低工人人数（如行政人员）；第2项反映不同规模下所需工人数，实体面积越大所需人数越多；第3 项反映每种技术创造的就业机会的数量；第4 项表示运输创造的岗位数量。

1.3 约束条件

模型约束条件具体定义与描述如下：

约束（1）和（2）表示正向物流和逆向物流中，原 材料与产品流量需对应，产品运输数量不超过产量。

约束（3）表示，工厂生产的产品数量需要满足市 场需求。

约束（4）和（5）表示了供应链网络中供应商的原 材料供应需满足自身供应量限制。

约束（6）～（9）表示，各实体流量同样受到自身流 量与容量限制。

约束（10）为等式约束，其作用是计算供应链网络模型流通过程中工厂和各仓库将要用到的库存面积，是通过当前库存水平和确保足以容纳流入的流量而确定的。

约束（11）表示实体可用面积应满足供应链网络仓储要求。

约束（12）～（13）分别限制实体可用面积在仓库整体可用面积最大值与最小值之间。

约束（14）和（15）分别表示承担收货方和发货方角色的实体，只有在实体被选择时才会有流量，这些约束也可以看作是最小流量约束，若参数存在特定下限，定义时则用最小的流参数乘以变量表示[如约束（9）]。

约束（16）保证了实体之间的流量不大于最大货物运输量。

约束（17）规定了运输方式下的最小货物运输量。

约束（18）～（19）规定了最大运输次数，且只有目的地被选择时运输才被激活。

约束（20）为等式约束，其目的是计算运输方式中交通工具数量最小值，约束（21）规定需满足约束（20）所计算出的最小值约束。

约束（22）表示卡车投入要小于对道路运输最大投资。

约束（23）和约束（24）分别保证只有在实体被选 择的情况下有流量时才使用交通工具。

约束（25）～（30）为技术约束，规定了生产和再制造技术产能在最小与最大生产水平之间，并同时规定了只有技术被选择时，该技术才有产能。

最后，约束（31）规定了一些决策变量的上下界。

2 算法设计

虽然已有文献开发多种算法求解优化问题，但是由于供应链网络的混合整数规划模型求解是个Nphard问题，目前还不存在一个完美的算法。粒子群优化算法（PSO）是一种随机化算法，其基本原理是随机选择一组粒子作为初始解，通过不断更新迭代粒子寻找最优解[20]。与遗传算法或蚁群算法等流行的启发式算法相比，PSO在寻找NP完全问题最优解方面具有相似的能力，但PSO需要较少的参数，具有更好的计算效率，非常适用于供应链网络优化问题[21]。因此，本文采用粒子群算法求解构建的模型。

传统PSO算法存在早收敛、陷入局部最优的缺点。为避免这一现象，在管理学领域内不少学者针对具体问题对算法提出了改进[21-24]。以往的研究对求解供应链网络问题的粒子群算法考虑较少，该问题具有高维度、多约束的特点，所设计的PSO算法不完全适用。因此，为了处理复杂的约束并减少算法陷入局部最优的可能性，针对上述所构建的供应链网络模型，对PSO算法进行了三处改进。在此之前为了便于叙述，在表3中列出了粒子群算法需要用到的符号。

表3 粒子群算法符号Tab.3 Notation of particle swarm algorithm

改进1：对粒子更新参数进行了改进。采用线性递增的惯性权重：

w_pso=wcmax_pso-(wcmax_pso-wcmin_pso)*(iter/itermax);

采用了线性递减的个体认知因子：

c1_pso=c1max_pso-iter*(c1max_pso-c1min_pso)/itermax;

采用了线性递增的群体学习因子：

c2_pso=c2min_pso+iter*(c2max_pso-c2min_pso)/itermax;

传统PSO算法中通过赋予w_pso、c1_pso、c2_pso固定数值，对粒子进行更新。与之相比，改进后的因子使得粒子在初期有较强的全局搜索能力，在后期有较好的局部搜索能力，降低了算法陷入局部最优的可能性。

改进2：基于惩罚函数法对模型各约束条件进行有效处理，修正模型目标函数。惩罚函数法是利用惩罚因子，将约束条件加到目标函数中构造增广目标函数，问题最终转化为无约束条件的增广目标函数求解。已有研究证明，当惩罚因子趋于无穷大时，增广目标函数的解将收敛到原目标函数的解[25]。具体操作步骤为：首先，设置数值较大的惩罚因子；然后，在计算各粒子适应度时，逐个判断各约束条件计算结果，若满足约束则将惩罚因子转换为0，否则将约束问题计算结果与惩罚因子相乘累加到目标函数中。

改进3：引入差别进化（DE）算法，对全部个体进行DE搜索。在处理高维复杂问题过程中，PSO算法受初始粒子群位置选择影响较大，容易过早停滞陷入局部最优。DE差别进化算法、遗传算法等启发式算法，可以对候选粒子进行交叉、变异等选择性操作，能够促使迭代中粒子跳出局部搜索，发生完全竞争，具有较强搜索能力。而DE编码方式与PSO相似，易于理解和实现[26]，所以将其与PSO结合可形成高效混合算法。结合改进1 和2，参考并调整文献PSODE思路，本文中的算法以PSO 算法的群体搜索策略为基础， 然后将粒子群中的全部个体用于DE搜索。

3 实证分析

3.1 数据收集与处理

以黑龙江某造纸企业为例，进行可持续闭环供应链网络研究。通过研究样本的企业管理者访谈、企业网站和企业年报等途径获取数据。确定参数后，利用加权目标规划法，将多目标转换为单目标。首先，记各目标最据进行归一化。最后，上述多目标模型可被等价转换为下式：

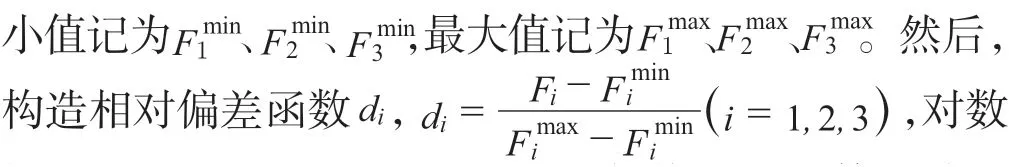
式中，ωi是各偏差函数所对应的权值，同时也代表子目标在企业实际生产过程中的优先级。管理者可对其进行调整，如果更关注经济目标，则将ω1赋予较大值，若更重视环境或社会效益则可对应提高ω2、ω3的值。ωi取值范围在0～1 之间，总和为1。

3.2 模型结果及分析

为验证算法有效性，假定各子目标同等重要，即权值相等，对模型求解。另外，为方便结果查看，权值全部赋值为1（相当于同倍数扩大），此操作不影响决策变量取值。利用Matlab2016a编写粒子群算法和改进粒子群算法代码，对模型求解，模型存在可行解，证明该模型在林产工业可持续闭环供应链多目标决策方面具备有效性。算法迭代收敛图见图2。

图2 迭代收敛图Fig.2 Iterative convergence graph

根据图中显示，PSO算法和改进PSO算法分别在200、400 次左右收敛，且改进算法的收敛效果优于初始粒子群算法，能够搜寻到更小的目标函数值。因此，可以使用改进算法对供应链网络模型进行求解。

为获得帕累托解（3 个目标在帕累托条件下的解），令权值ω1、ω2、ω3在0 到1 之间进行变动，每次运行以0.1 步长增加经济目标权值，同时确保3 个目标权值之和为1，生成66 种权值组合。分析所有权值组合下的目标函数值，结果如图3 所示。

图3 多目标帕累托最优解Fig.3 Multi-objective Pareto optimal solution

如图2 所示，x轴是以总成本表示的经济目标值；y轴以总碳排放量和水资源消耗量加权平均表示的环境目标值；z轴是以提供工作岗位数量表示的社会目标值。上部圆圈的点代表所有的求解结果，底部星号的点为上部圆圈点在xy轴平面上的投影。每个圆圈的点代表一个帕累托解决方案，点的坐标由3 个值来表示，每个值对应于该方案在3 个可持续性维度的表现。在对应维度表现好则说明赋予权值越大。

基于可持续性维度，企业战略目标可分为经济导向型、环境导向型和社会导向型，各类型通过调整对应子目标权值体现。不难分析出，三个目标是矛盾的，无法同时达到最优。企业管理者根据各权值组合下的模型计算结果，能够看到不同战略目标决策方案下各子目标的具体状态。据此，企业决策者可做出更理性的选择。例如，若不考虑社会维度，追求绿色供应链，即追求经济与环境的平衡优化，可以选择A处的生产决策；若以社会导向型为战略目标，对创造的就业机会数量更加关注，则应该在B处进行选择，因为与其他位置的点相比，就业机会数量相对较高，且实现了降低污染、减少成本的目的，三个目标表现出良好的平衡。

对上述结果进一步处理，计算偏差函数，分析经济成本变动时的环境与社会效益变动浮动（图4）。

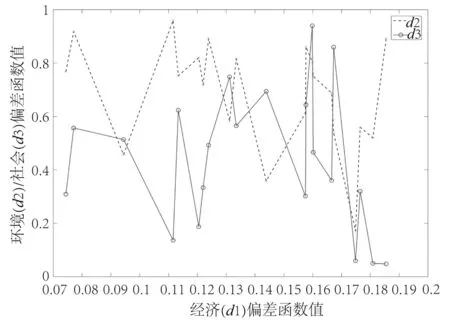
图4 成本变动下的环境和社会目标变化Fig.4 Changes in environmental and social objectives under cost variation

图4 显示了当决策者支付更高的经济成本时，运行方案在环境和社会方面的改进程度。当经济成本偏差函数（d1）在0～0.2 之间变动时，环境偏差函数（d2）与社会偏差函数（d3）分别在0.06～0.96 与0.04～0.93之间变化。上述过程呈现出一定的波动性，成本与社会、环境目标不是简单的线性关系，这也体现出了供应链网络的复杂性。具体成因如下：根据模型所设定环境目标和社会目标函数，环境受产量、技术、运输方式的影响，增加产量、选用先进技术或高效节能运输方式都会提高成本，前者会增加碳排放和资源消耗，从而对环境效益产生负效应，后两者则会减少环境有害提高环境绩效，所以成本增加作用在环境绩效上的综合效用是无法直接判断的，社会目标函数也是如此。因此，决策者在确定生产方案前可根据产品、技术及运输参数，结合企业阶段性发展要求选择最佳的帕累托解进行供应链优化。

4 结论

本文以林产工业中造纸及纸制品制造业作为研究对象，以经济成本最小、环境影响最小和社会效益最大为目标，建立纸制品多目标闭环供应链网络模型。结合该模型，改进粒子群算法，在Matlab中编程求出最优解。主要得到以下结论：

1）改进的粒子群算法求解效果良好，收敛速度快且寻优结果更佳，为林产工业及其他行业的供应链网络模型求解提供参考；

2）设计的多目标混合整数规划模型可帮助企业管理者决策，确定企业不同战略目标（经济导向型、环境导向型和社会导向型）下的生产方案，得知需要付出的准确成本；

3）求解的模型结果可作为资源配置和结构优化的依据，当决策者需要做出选择时，如是否引进技术、更换运输方式等，能够依据具体设备参数，利用模型求解结果做出更符合企业发展目标的决策。