基于改进粒子群优化算法的外转子永磁同步电机的多目标优化设计

乔路宽， 张炳义， 李 岩， 冯桂宏

(沈阳工业大学 电气工程学院，辽宁 沈阳 110870)

0 引 言

永磁同步电机具有效率高、功率密度高、容错性能强、结构简单可靠等优点，广泛应用于各行各业[1-3]。对于外转子永磁同步电机(ERPMSM)，转子在外侧而具有转动惯量大、结构紧凑等特点，可直接驱动皮带输送机运转，成为皮带输送机驱动电机的主要选择[4-5]。

皮带输送机早期采用头部集中驱动方式，但由于驱动电机处皮带张力受限导致皮带输送机无法大型化。为此，多点驱动式皮带输送机应运而生，最常见的有直线摩擦式和转载式[6]两种。将传统皮带输送机的传动托辊替换成永磁动力托辊可减少皮带张力，延长皮带输送机单机设计长度，国内外对此研究相对较少。本文针对长距离皮带输送机的驱动电机采取化整为零的思想，可以根据实际工况计算出驱动功率自行选择永磁托辊数量，进而皮带输送机用电机可以批量化生产，使电机真正作为皮带输送机的一部分。

随着皮带输送机继续大型化，所需驱动电机数量会成倍增长，每个驱动电机的成本较大程度地影响着皮带输送机的造价，而永磁体成本又占据永磁电机造价成本的绝大部分。因此，减少永磁体成本可以大幅度降低整台皮带输送机的生产费用，但减少永磁体的用量会导致电机性能降低，因此采用多目标优化设计的方法，兼顾电机永磁体成本与电磁性能十分必要。

在永磁同步电机的多目标优化设计方面，文献[7]采用响应面法实现永磁电机的感应电动势、感应电动势谐波以及齿槽转矩的优化。虽然响应面法可以实现多目标优化的目的，但由于其本身的局限性，需要采集足够多的样本才能保证优化算法的准确性，但这种情况下会导致优化效率不高。文献[8]采用田口法得到永磁同步电机的转矩密度、效率以及齿槽转矩的最优值，田口法的主要问题是计算精度差、全局性差，且无法考虑到优化目标之间的相互制约关系。文献[9]采用二代非支配排序遗传算法(NSGA-II)对输出转矩、效率和转矩脉动同时进行优化，虽然NSGA-II具有较强的全局寻优能力，但是该算法收敛速度慢、优化效率不高。文献[10]通过Kriging模型结合多目标粒子群算法优化了永磁电机的齿槽转矩、电磁转矩以及永磁体成本，但是传统的多目标粒子群优化(MOPSO)算法容易过早陷入局部最优解，导致优化结果不精确。目前，常用的多目标优化算法包括蚁群算法、粒子群优化算法和遗传算法等。其中，粒子群优化算法相比于其他优化算法，具有记忆能力强、算法简单、收敛速度快等优势[11]，因此广泛应用于电机的多目标优化设计。

为解决传统MOPSO算法容易过早陷入局部最优的难题，本文在其基础上引入非线性递减自适应惯性权重、基于拥挤距离法的外部档案维护机制以及变异操作，改进多目标粒子群优化算法(IMOPSO)可以有效克服这一缺点。因此，本文结合响应面法(RSM)和IMOPSO对ERPMSM进行多目标优化设计，兼顾永磁体成本与电磁性能，并通过有限元仿真验证了多目标优化设计的正确性。

1 ERPMSM基本结构

图1为10极12槽ERPMSM的原始模型。电机尺寸较小，转子外径仅为117 mm，永磁体很难固定，因此选择在转子处开设燕尾槽。在便于固定的同时缩短电机的单边气隙长度，节约永磁体用量。但其缺点是燕尾槽处漏磁较多，导致定子磁链变小，进而输出转矩减小。同时在开设燕尾槽后，转子设计为凸极转子结构，由于电机转子磁路不对称而产生磁阻转矩，导致转矩波动变大[12]。

图1 ERPMSM模型

另外，本文的ERPMSM是作为传统皮带输送机承载托辊的替代品，是皮带输送机装备的一部分，因此在轴向和径向的尺寸上必须满足皮带输送机用承载托辊的国标要求。与传统永磁电机的多目标优化设计相比，需要固定电机的的径向与轴向尺寸，仅从ERPMSM的定子槽型尺寸、永磁体尺寸和气隙长度等结构方面进行考虑，电机的初始设计参数如表1所示。

表1 ERPMSM参数

2 IMOPSO

传统MOPSO具体流程如图2所示。随机初始化一组粒子，并将计算后得到的非劣解存入外部档案Np中，然后根据获得的粒子局部最优位置pi和全局最优位置pg更新粒子群的位置和速度，最后根据新的非劣解维护Np、选取新的pg，直至满足终止条件[13]。

图2 MOPSO流程图

对于MOPSO，在给定D维的搜索空间，粒子群由n个粒子组成，其中，第i个粒子的D维位置矢量可表示为xi=[xi1xi2…xiD]，第i个粒子的速度矢量为vi=[vi1vi2…viD]，粒子的局部最优位置矢量为pi=[pi1pi2…piD]，粒子群全局最优位置为pg=[pg1pg2…pgD]。第i个粒子的速度和位置更新算式为

(1)

(2)

式中：w为惯性权重；c1和c2分别对应自我认知因子和社会认知因子；r1和r2代表分布在0～1之间的随机数。

MOPSO的主要缺点是粒子易陷入局部最优解，本文做出如下创新以改进算法，并利用测试函数证明改进算法的优越性。

2.1 惯性权重的改进

MOPSO的惯性权重w影响算法的搜索能力，因此常用线性递减原则改进w，使算法在前期增大从而增加对搜索空间的搜索，在后期减小w提高算法的局部搜索能力，防止陷入局部最优解。但是w的这种变化与算法的运行状态互相独立，难以适用于求解非线性或者较为复杂的问题。所以本文采用自适应非线性递减的原则来改善算法的收敛性能，使w随着算法的迭代次数产生非线性递减。新的惯性权重可以表示为

(3)

式中：T为最大迭代次数；k为当前迭代次数；λ1和λ2为控制参数，本文分别取0.33和4，使w从0.9非线性递减到0.4。

2.2 基于拥挤距离法的外部档案维护机制

与单目标粒子群优化算法不同，MOPSO需要建立外部档案库来储存非劣解。本文引入拥挤距离的概念，对MOPSO进行改进。对于拥挤距离的求解，以双目标优化问题为例，拥挤距离的计算方法如图3所示，第m个非劣解的拥挤距离即为虚线围成矩形的1/2周长。在迭代过程中，外部档案库已满的情况下，通过计算并淘汰拥挤距离最小的非劣解对外部档案进行维护，保持种群多样性并进一步加快迭代速度。

图3 MOPSO流程图

2.3 引入变异操作

粒子群优化算法具有较强的全局收敛能力，在求解多目标问题时，收敛速度快会导致过早收敛，容易陷入局部最优解。因此，在粒子迭代过程中，通过引入变异操作可以提高种群多样性，防止粒子早熟收敛。在粒子位置更新的过程中，有10%的概率进行变异操作，如下所示：

(4)

式中：xk为迭代过程中粒子位置矢量；xkmax和xkmin分别为位置矢量的最大值和最小值；rand为0～1的随机数；Fg为自适应变异算子。

随着迭代次数的增加，变异算子的影响效果逐渐减弱，Fg表达式为

Fg=[rand·(1-k/T)]2

(5)

2.4 改进前后算法的性能对比

为了验证IMOPSO的优越性，将其与线性递减权重和固定权重的MOPSO算法进行比较。选取测试函数DTLZ3，种群数量为300，迭代次数为500，各算法运行10次，并以世代距离(GD)和间距指标(SP)评估算法性能。

其中，GD是评估算法收敛性能的指标，表示算法已经搜寻到的非支配解集与实际Pareto前沿的距离，其计算式为

(6)

式中：N为非支配解集规模；di表示第i个个体到实际Pareto前沿的最短欧式距离。

GD越小，表示算法的收敛精度越高。

SP是评估算法多样性的指标，用以表示算法所得到的非支配解在目标空间中分布的均匀程度，其计算式为

(7)

非支配解在目标空间中分布的越均匀，SP的值就会越小。

由表2的测试结果可以发现，优化后的IMOPSO的GD和SP均小于其他两种优化算法。因此，证明IMOPSO具有更好的收敛性和多样性。

表2 优化算法性能对比

3 ERPMSM多目标优化

多目标优化问题是指同时存在多个需要被优化的目标，且彼此间互相影响。多目标优化可能存在一个或多个解，是考虑各个优化目标之后确定的最优解。ERPMSM的具体优化流程主要包括优化目标与优化参数的确定、参数灵敏度分析、响应面建模和IMOPSO寻优四个步骤。

3.1 确定优化目标与优化参数

为了兼顾ERPMSM的永磁体成本和电磁性能，将ERPMSM的永磁体成本Cpm、相反电动势总谐波畸变率(THD)、转矩脉动系数KR、输出转矩TN和相反电动势有效值E0作为优化目标。

电机的输出转矩TN可以表示为

TN=Tpm+Tr+Tcog=

(8)

式中：Tpm为永磁转矩；Tr为磁阻转矩；Tcog为齿槽转矩；p为极对数；Ld和Lq为d轴和q轴电感；Id和Iq为d轴和q轴电流；ψpm为永磁磁链。

本文的dq轴电感相差不多，因此齿槽转矩Tcog对转矩脉动具有较大的影响。齿槽转矩表达式如下所示：

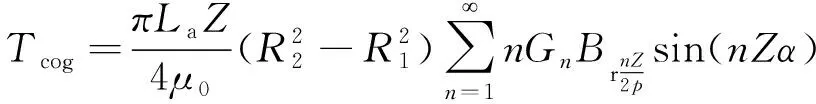
(9)

改变电机的定子参数和磁极参数可以改变二者的幅值，进而达到削弱齿槽转矩的目的。

在轴向长度La固定的情况下，永磁体成本Cpm取决于永磁体的宽度和厚度，采用不均匀气隙可以优化相反电动势波形，对相反电动势的THD以及有效值均有一定的影响。最终确定永磁体宽度bm、永磁体厚度hm，槽口宽度bs0、齿宽bt、槽深hs和气隙长度δ作为优化参数。表3给出优化参数的合理取值范围。

表3 优化参数取值

对于优化目标的约束条件，包括：

(10)

通过加入惩罚函数将之引入目标函数f(x)中，构成增广目标函数F(x)，可表示为

(11)

式中：αi为惩罚因子；Pi(x)为满足对应约束条件下的惩罚函数。

3.2 灵敏度分析

为了减小试验次数与减轻计算复杂程度，需要先对上述6个优化参数进行灵敏度分析。本文通过确定性筛选设计获得试验数据[14]，并采用基于方差的灵敏度分析方法，测量每个变量对响应值的灵敏度指数，第i个优化参数对第j个优化目标灵敏度Sj(Xi)计算方法如下所示：

(12)

式中：Xi为第i个优化参数；Yj为第j个优化目标；E(Yj/Xi)为Xi固定时Yj的平均值，V[E(Yj/Xi)]是其方差；V(Yj)为Yj的方差。

本文涉及5个优化目标，且每个优化参数对优化目标的敏感程度都不同，会给灵敏度分析的后续筛选带来困难，因此将多目标的灵敏度分析转化为带权重系数的综合灵敏度分析，其指数可表示如下：

(13)

式中：Qj为不同优化目标的权重系数，分别取0.2、0.2、0.3、0.2、0.1。

灵敏度分析结果如表4所示。

由表4可知，bm、hm、bs0和δ更为显著，将结果进一步优化，非显著参数通过单参数优化进行确定。

表4 灵敏度分析结果

3.3 响应面建模

RSM利用有限元仿真试验获得的数据进行拟合，建立了反映各个优化参数与优化目标之间数学关系的模型[15]。本文采用二阶多项式回归方法来建立响应面模型，其具体形式可以表示为

(14)

式中：Y为优化目标；b0为常数项；Xi、Xij为对应不同的优化参数；bi、bij和bii为优化参数的一、二次项系数；ε为随机误差。

通过灵敏度分析后的显著变量水平如表5所示。采用有限元仿真软件进行试验，四个变量的Box-Behnken设计(BBD)需要进行29次试验。

表5 显著变量水平

通过Design-Expert对结果数据进行分析，得到多目标优化函数如下：

THD=92.12-8.06bm+7.67hm-7.65bs0+8.03δ-0.29bm×hm+0.31bm×bs0-

KR=269.17-22.06bm-2.5bs0+5.81δ-0.12bm×hm+0.2bm×bs0-1.34bm×δ-0.11hm×bs0+4.43hm×δ+

Cpm=-310.59+12.9bm+119.29hm

TN=9.61+0.16bm+2.58hm-0.16bs0-

E0=21.94+11.62bm+44.05hm-1.93bs0-

107.61δ+0.11bm×hm+0.08bm×bs0+1.1bm×

δ+0.17hm×bs0+15hm×δ+0.14bs0×δ-

(15)

对目标模型进行的评估如表6所示，THD、KR、TN和E0的二次模型的P值均远小于0.01，且信噪比大于4 dB，表示模型显著性很好，可信度较高。Cpm的线性模型中的P值远小于0.01，且信噪比远大于4 dB，表示显著性很好，可信度很高。另外，5个优化目标的R2均大于0.9，这表明响应面与真实值之间的差异较小，且模型中没有统计学意义的变量数很少，进一步证明模型的拟合度较好，数据规律可以被模型较好地反映。

表6 响应面法分析结果

3.4 IMOPSO

采用MATLAB软件编写上述IMOPSO程序，设置种群规模和外部档案均为50，迭代次数为200，粒子的c1和c2均取1.499 5，运行程序得到如图4所示的Pareto前沿。

图4 Pareto前沿

图4中以每个粒子的大小来表示输出转矩TN的值，并以xy平面投影的大小来表示E0的值。综合考虑后，在所有Pareto解中选出可行解，在确定了显著优化参数之后，将非显著优化参数单独分析得出优化方案。

4 优化结果分析

将优化后方案与优化前方案进行对比，结果如表7所示,有限元仿真结果如图5～图8所示。

表7 优化参数与优化目标对比表

本文的ERPMSM的轴向长度固定，永磁体的成本仅与永磁体的厚度hm和宽度bm有关。由表7可知，优化后方案的永磁体宽度由26.0 mm减小至23.8 mm，永磁体厚度由2.5 mm减小至2.3 mm，永磁体体积减小，永磁体成本比优化前降低了19%。

与初始方案相比，IMOPSO优化方案的槽口宽度bs0从3.6 mm减小至2 mm。由图5～7可知，由于槽口宽度减小，齿槽效应减弱，ERPMSM的相反电动势THD减少了56.5%，转矩脉动减少了54.6%。由图7和图8可知，由于气隙长度δ从0.7 mm减小至0.6 mm，气隙磁密有所提高，额定转矩提高了2.3%，相反电动势有效值提高了0.6%。

图5 优化前后气隙磁密对比

图6 优化前后空载相反电动势谐波对比

图7 优化前后转矩对比

图8 优化前后空载相反电动势对比

由结果可知，IMOPSO优化算法求解的优化设计结果与有限元仿真结果具有良好的一致性，证明此算法准确可靠。通过本文所提IMOPSO算法进行优化后，ERPMSM的永磁体成本降低，电机的电磁性能得到了优化，证明了IMOPSO算法的有效性。

5 结 语

本文针对长距离皮带输送机用ERPMSM的多目标优化展开研究，提出了一种基于RSM和IMOPSO的ERPMSM优化设计方法，并对优化后的方案进行仿真验证，得出以下结论：

(1) 本文提出的IMOPSO，有效地解决了MOPSO迭代后期粒子容易陷入局部最优解的问题，并通过测试函数DTLZ3验证了算法的优越性。

(2) IMOPSO优化后的方案相比于初始设计方案来说，空载相反电动势谐波THD减少了56.5%，转矩脉动减少了54.6%，永磁体成本降低了19%，额定转矩提高了2.3%，相反电动势有效值提高了0.6%。

(3) 本文提出的IMOPSO准确可靠，且具有更好的收敛性和多样性，能够在减少永磁体成本的同时优化电机性能。