脉冲发电机鲸鱼优化自适应PID励磁控制
赵强强, 李华俊, 叶 强
(核工业西南物理研究院,四川 成都 610225)
0 引 言
大功率脉冲发电机常应用于托卡马克装置、激光雷达、电磁轨道发射等需要短时大功率能量的场景[1-2]。脉冲发电机机端电压的稳定性是其供电质量的重要指标,对所带负载以及所带二次电源的工作性能均起着决定性的作用。放电过程中,脉冲发电机的转速快速下降和负载电流的突然增加均会引起机端电压剧烈下降,此时只有通过施加额定励磁电压才能使其机端电压快速恢复,即脉冲发电机的励磁控制系统应具有较高的响应速度,且具有一定维持额定输出的作用。为提励磁控制的响应速度,高性能的处理器[3-4]、优化控制[5]应用于励磁控制系统中,但基于反馈的优化控制无法突破反馈控制固有的滞后特性,为此有文献[6]在励磁系统中引入了前馈控制,该方法较好地提高了励磁控制的动态响应,降低了负载电流增大时的电压降落,但并未考虑发电机转速下降带来的扰动。
本文从反映发电机转速对电机参数影响的有名值模型出发,通过使用机端电压、输出电流、以及转速等脉冲发电机的运行变量来实现对发电机的暂态电动势的观测,最后得到了以变化的暂态电动势为给定值,包含电流扰动的单输入单输出线性控制系统模型。之后为提高控制系统的响应速度和稳态精度,采用了随误差动态变化的参数自适应的PID控制。对于自适应PID参数的整定,构建了以绝对误差积分(IAE)为优化目标,控制器参数为优化变量的优化问题,并使用鲸鱼优化算法(WOA)对该优化问题进行求解。最后,通过仿真验证了所提方法的有效性。
1 脉冲发电机励磁控制系统模型
1.1 六相脉冲发电机
六相脉冲发电机为六相同步发电机,结构上采用了大惯性的转子轴系来储存能量。将储存在转子轴系上的动能转化为电能,供给脉冲负载,避免了大功率脉冲负载直接从电网取电而造成的对电力系统的冲击。脉冲发电机在放电的过程中由于飞轮能量的释放从而使转速持续下降,使发电机电抗参数变化。因为脉冲发电机所带的负载类型通常为无源负载,与用于电力系统的负载为恒电压负载的同步发电机不同,所以发电机模型采用阻感参数表示的有名值二阶模型,包括励磁绕组电压方程和转子运动方程:
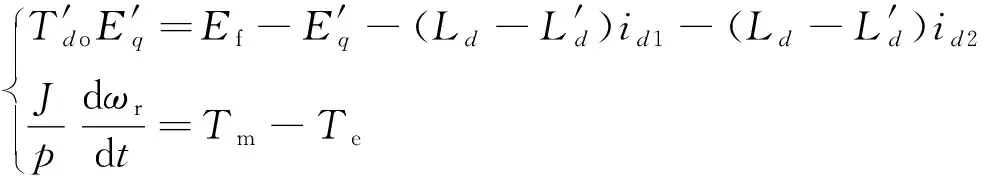
(1)
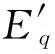
发电机的电磁电转矩方程为
(id1iq1+id1iq2+id2iq1+id2iq2)
(2)
发电机的输出电压可以表示为
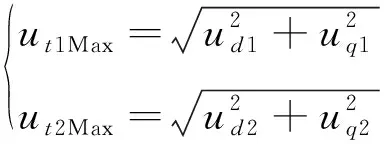
(3)
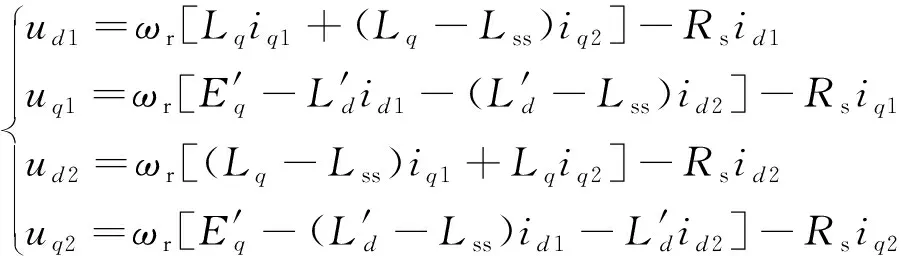
(4)
式中:ut1Max、ut2Max分别为1Y绕组电压和2Y绕组电压的最大值;ud1、uq1、ud2、uq2分别为1Y绕组和2Y绕组的d轴和q轴电压分量;Lss为定子绕组的自漏感;Rs为定子绕组电阻。
1.2 线性化
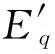
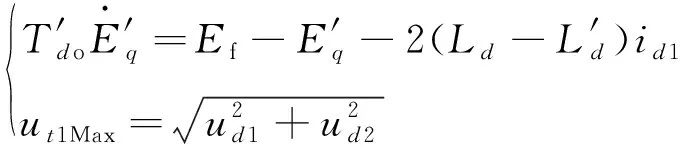
(5)
由式(5)可以看出脉冲发电机状态方程不仅为线性方程,而且其不包含扰动ωr。扰动变量ωr和系统的非线性环节均集中在输出方程中,而输出方程为代数方程,显然易从输出方程中反解出状态变量:
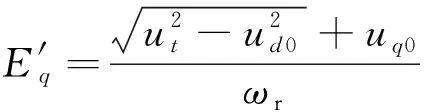
(6)
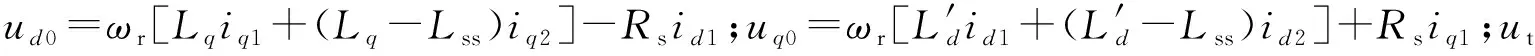
最后得到包含励磁功率单元和测量回路的脉冲发电机励磁控制系统的控制框图如图1所示。
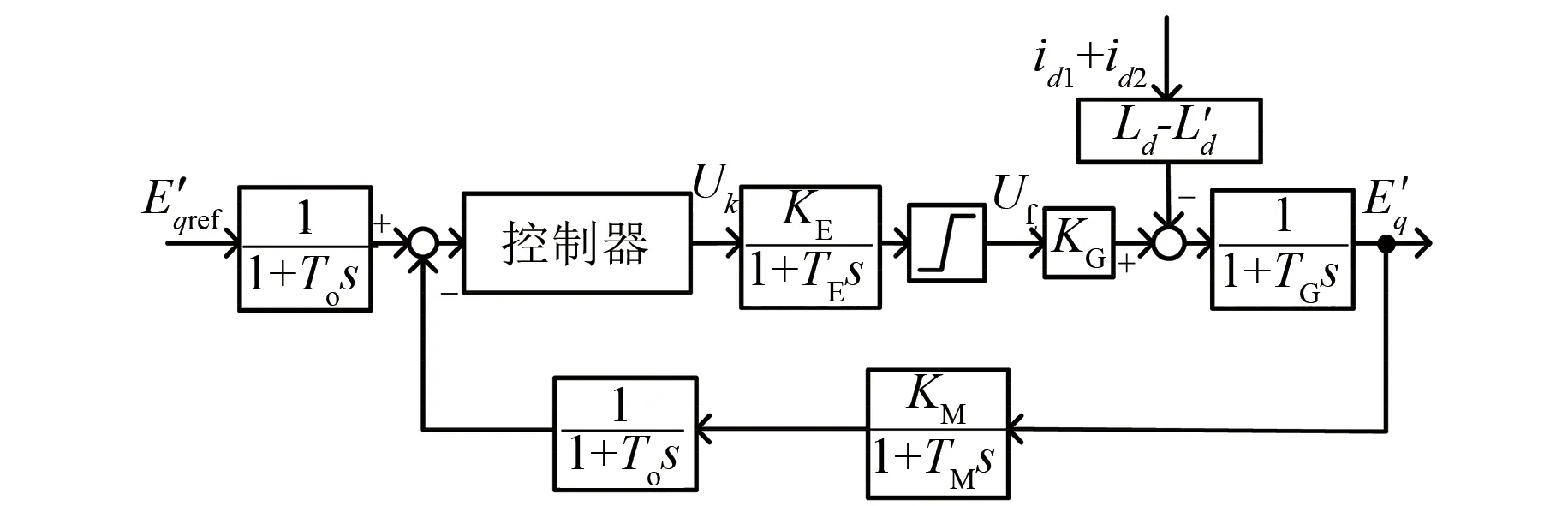
图1 脉冲发电机励磁控制系统框图

从简化后的励磁控制系统的框图图1可以看出,该控制系统为包含扰动输入的单输入单输出线性系统,从而便可以运用经典控制理论的系统设计和分析方法对系统进行矫正、分析,且控制器的设计不会受到系统工作点的影响。系统的传递函数为多个惯性环节串联,发电机模型的惯性时间常数较大,其余均为小惯性环节,所以整个系统表现为大惯性系统。
2 鲸鱼优化的自适应PID控制
对于单输入单输出线性系统的控制,常采用基于经典理论系统矫正的PID控制器。PID控制器原理简单、实现方便,在工业控制领域具有广泛的应用。发电机带脉冲负载时,其工作时间很短,在几毫秒到几秒之间,对控制器的快速性有着更高的要求。而对于大惯性系统的控制,为提高系统的动态响应能力,往往采用高增益的控制器,控制器的增益过大会使系统对噪声扰动变得敏感,不利于系统的稳定运行。因此,本文根据脉冲发电机的工作特点以及PID 控制器的原理,提出一种基于误差的参数自适应PID。当系统的误差较大时,设计控制器参数使控制器增益较高,使系统的误差快速减小;当系统的误差较小时,控制器恢复正常的运行状态,维持系统的稳定运行。
通过PID控制器参数的动态调节,提高大惯性系统的动态响应,同时保证系统正常运行的稳定性。但这意味着控制器引入更多的参数,因为PID各个环节输出调节的同时,还要进行各环节参数的调节,使控制器参数的整定更加复杂。WOA是一种模拟座头鲸捕食行为的智能搜索算法,在PID控制器的参数寻优能力较好。因此,本文使用WOA对参数自适应PID控制器的多个参数进行寻优。
2.1 参数自适应PID控制
位置式离散PID的控制规律:
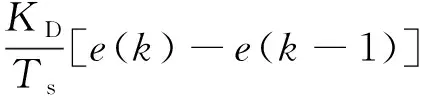
(7)
PID控制有比例环节、积分环节以及微分环节构成,相应的KP、KI、KD为比例系数、积分系数和微分系数,PID控制的整定即为确定KP、KI、KD的值,使系统达到预期的控制效果:
(1) 比例环节:直接根据当前的误差进行控制,误差越大时比例环节的输出也越大,当误差为0时,比例环节的输出为0。比例系数KP用来调整比例控制的权重,当比例系数过小时,当前的误差项在输出控制量占比较小,从而使系统的误差无法快速消除,快速性较差;当比例系数过大时,会使系统对于误差信号过于敏感,从而发生高频振荡。
(2) 积分环节:根据误差的累积量进行调节,只要当误差存在时,积分环节的输出也一直变化,直到误差为0 时,积分环节的输出保持为恒定值。当积分系数过小时,累计误差的控制效果不够明显,从而使得稳态时系统的稳态精度较低;当积分系数过大时,积分项控制输出太大,且由于积分的延迟特性使系统发生低频振荡,此外还会使积分环节进入饱和,从而一段时间内积分环节的调节效果失效。
(3) 微分环节:根据误差的变化量进行调节,当误差减小时,微分环节的输出为负;当误差增大时,输出为正,微分环节表现为对误差变化的抑制,起到阻尼的作用;当微分系数过大时,使控制输出的抑制效果增强,从而使误差变化缓慢,使系统的调节时间增大。对于一般的控制系统,往往设置较小的KD,或者使KD=0构成PI控制。
从以上分析可以得出,想要提高系统的快速性,需要增大KP、KI,减小KD,而KP、KI的增大又会使系统引起不同程度的振荡,这与系统的快速性矛盾。而脉冲发电机的工作特点又需要系统有较好的动态性能,使脉冲发电机的机端电压快速达到负载的供电需求,同时也减少系统在调整过程中的能量损耗,提高脉冲发电机的输出效率。因此,考虑使用参数自调节的PID控制方法:
(1) 当系统的误差较大时,采用较大的比例系数KP和积分系数KI来增大控制器的输出,使控制器快速达到饱和,实现误差较大时系统的快速响应。
(2) 当系统的误差较小时,使用稳态运行的PID控制参数,来提高系统的稳定性,抑制振荡。
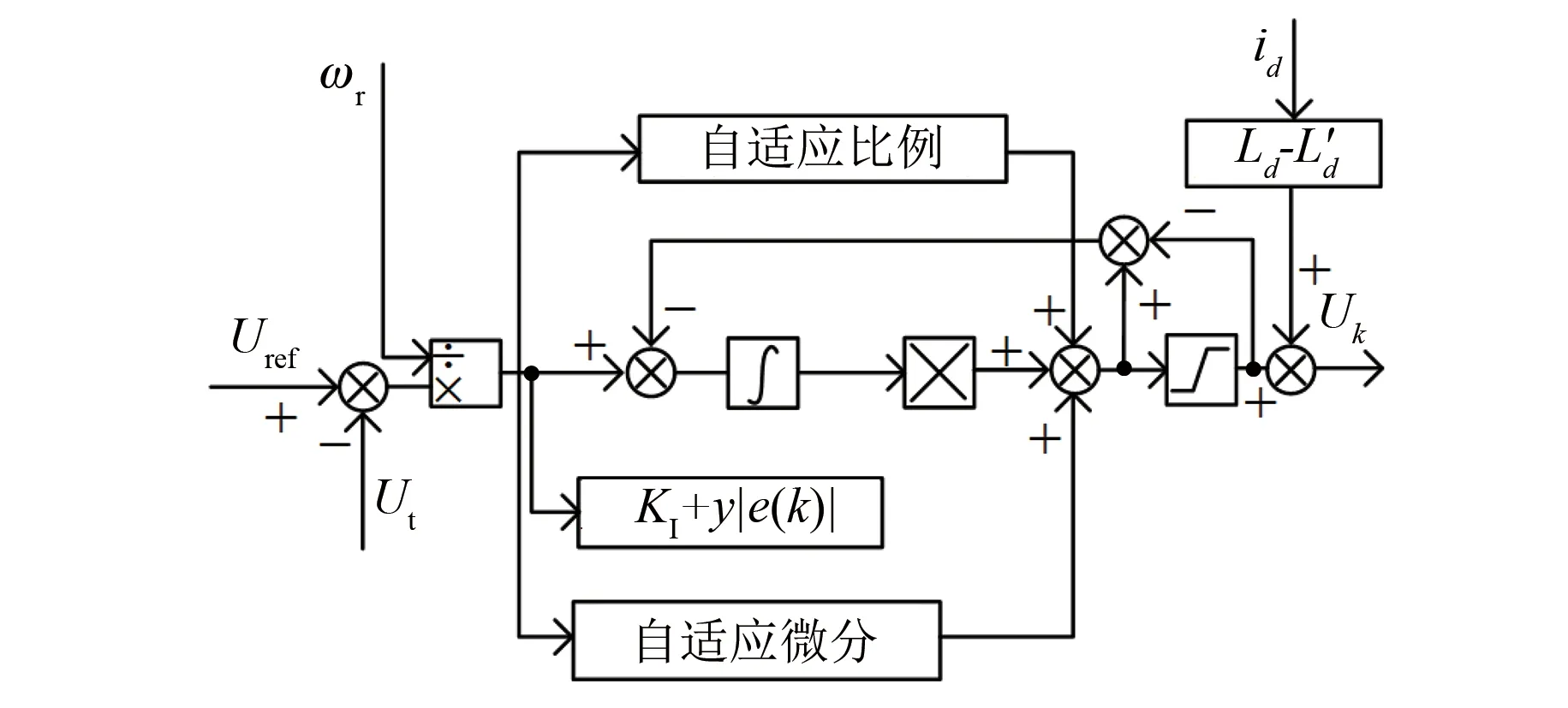
从而得到参数自适应PID控制规律,如图2所示。

图2 自适应PID控制原理框图
据图2有表达式如下:
u(k)=[KP+x|e(k)|]e(k)+
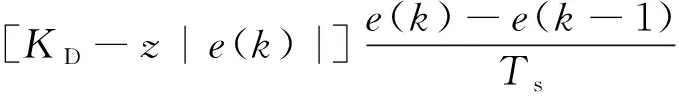
(8)
式中:KP+x|e(k)|、KI+y|e(k)|、KD-z|e(k)|分别为自适应比例系数、自适应积分系数、自适应微分系数。
在调节系数中通过引入当前误差项,使控制器在误差较大时,获得较大的比例系数和积分系数,以及较小的微分系数,使控制器输出快速增大,从而实现快速调节的目的。而当误差消失之后,调节系数又恢复到原来的值,保证了系统的稳定运行,而不发生振荡。
2.2 WOA设计
2.2.1 算法原理
WOA是一种模拟座头鲸捕食行为的智能优化算法。座头鲸在捕食过程通过吐出螺旋上升的气泡将猎物包围并逐渐收紧,从而将聚集到气泡网顶端的所有猎物吞食。通过模拟座头鲸气泡网捕食行为,来更新智能个体的位置,该智能搜索方法称为WOA,该算法的流程如图3所示。
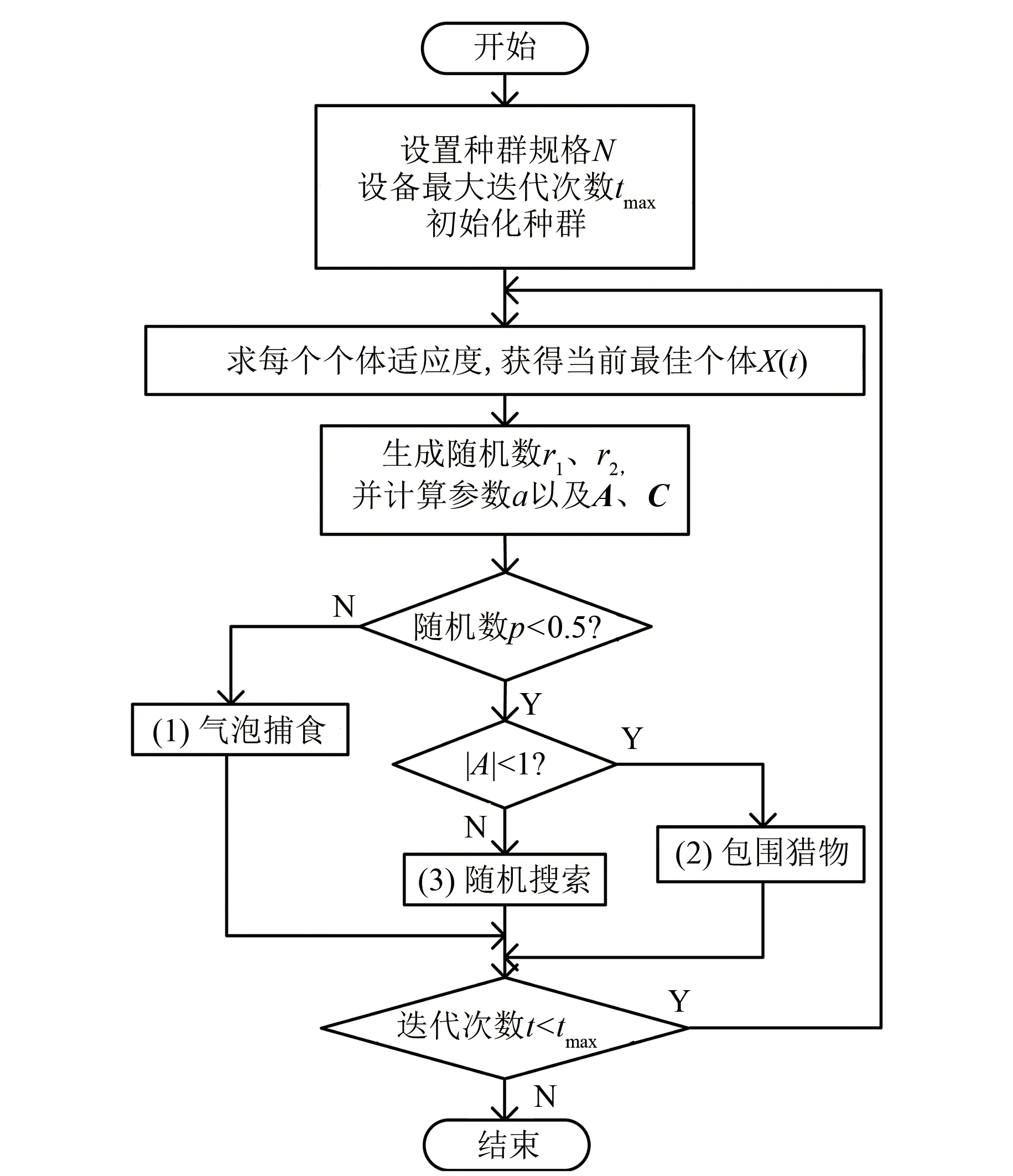
图3 WOA原理流程图
参数:A=2a·r1-a,C=2r2,图3中r1和r2是[0,1]的随机向量,a随着迭代次数的增加从2下降到0。
WOA在搜索过程中通过随机数p和随机向量A来决定智能个体的行为:气泡网捕食、包围猎物以及随机搜索。
(1) 气泡网捕食。智能个体以螺旋方式向最佳个体靠近:
X(t+1)=D′·eBl·cos(2πl)+X*(t)
(9)
式中:D为智能个体到目标个体之间的距离向量,该阶段的目标个体为最佳个体,D=|X*(t)-X(t)|;B为螺旋形状参数;l为[-1, 1]之间的随机数。
(2) 包围猎物。使所有智能个体向最佳个体线性靠近:
X(t+1)=X*(t)=A·D
(10)
式中:D′=|CX*(t)-X(t)|。
(3) 随机搜索。使智能个体向随机个体线性靠近:
X(t+1)=Xrand(t)-A·D
(11)
式中:D″=|Xrand(t)-X(t)|。
2.2.2 问题描述
控制方法参数优化的目的是为了提高控制器的性能,改善系统的动态响应指标。常见的控制系统的优化函数有误差绝对值积分、带时间权重的误差绝对值积分、误差平方积分和带时间权重的误差平方积分。为了能够更好地反映大惯性系统的快速性的特征,本文采取带时间权重的误差绝对值积分,于是优化目标为

(12)
优化变量为式(8)所示的控制方法调节系数KP、KI、KD以及调节系数x、y、z。
等式约束为图2所示的控制系统的框图和式(8)所示的控制方法。
不等式约束:
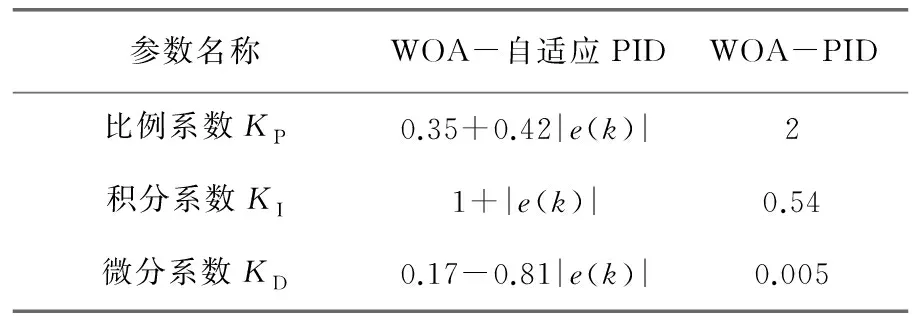
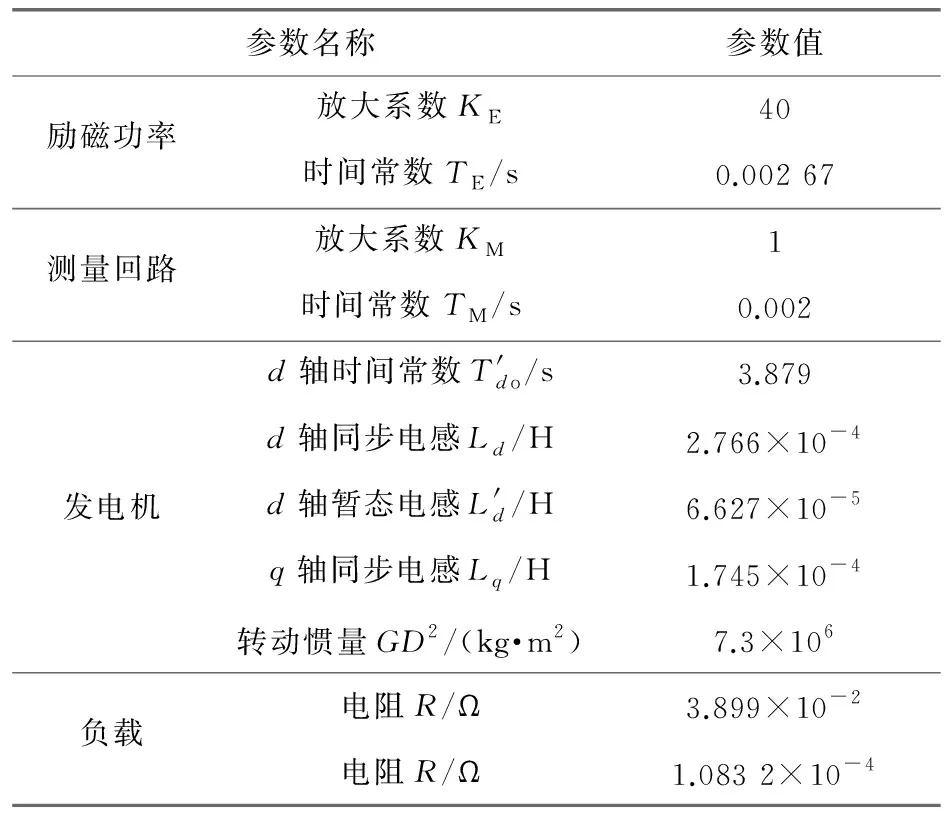
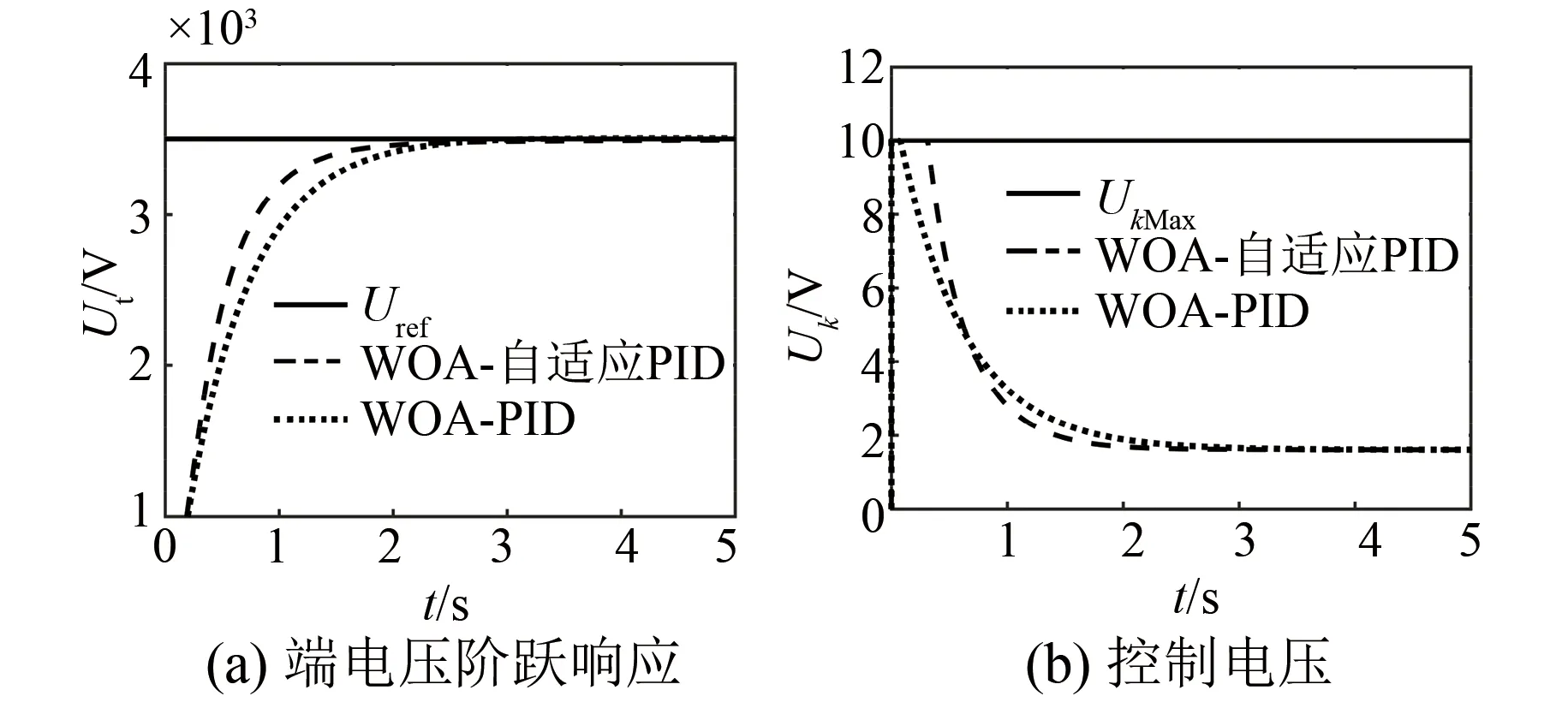
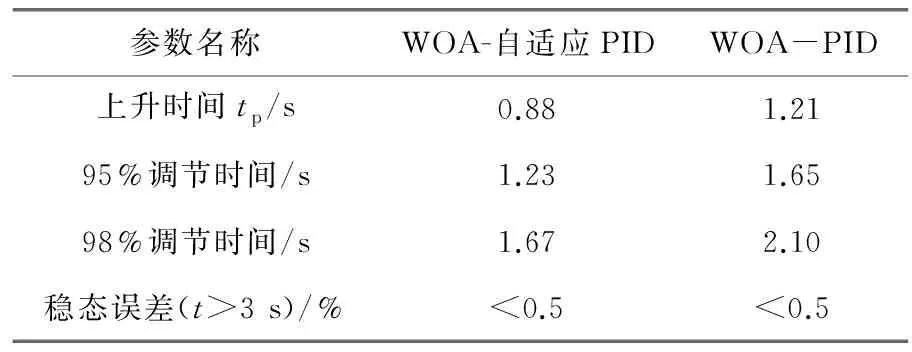
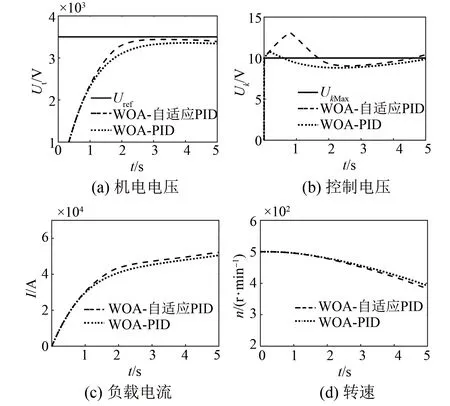
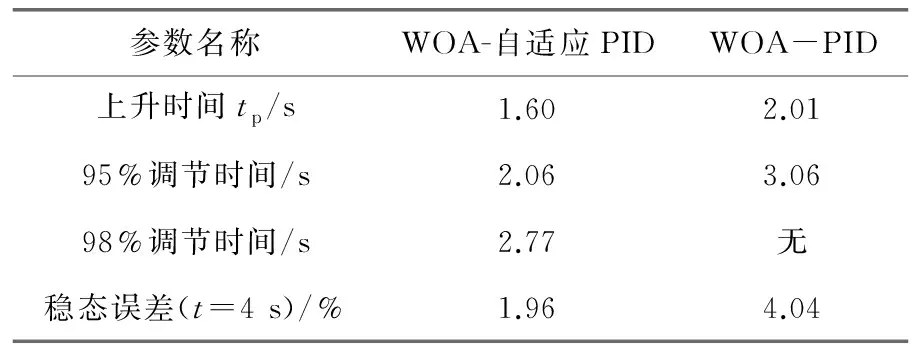
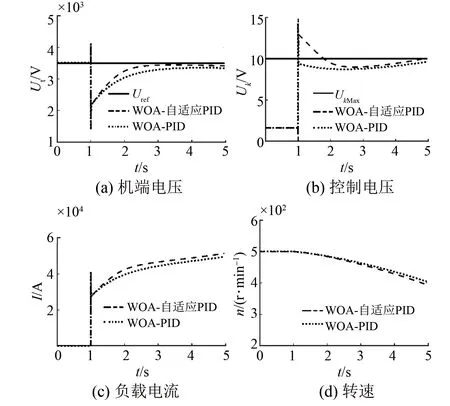
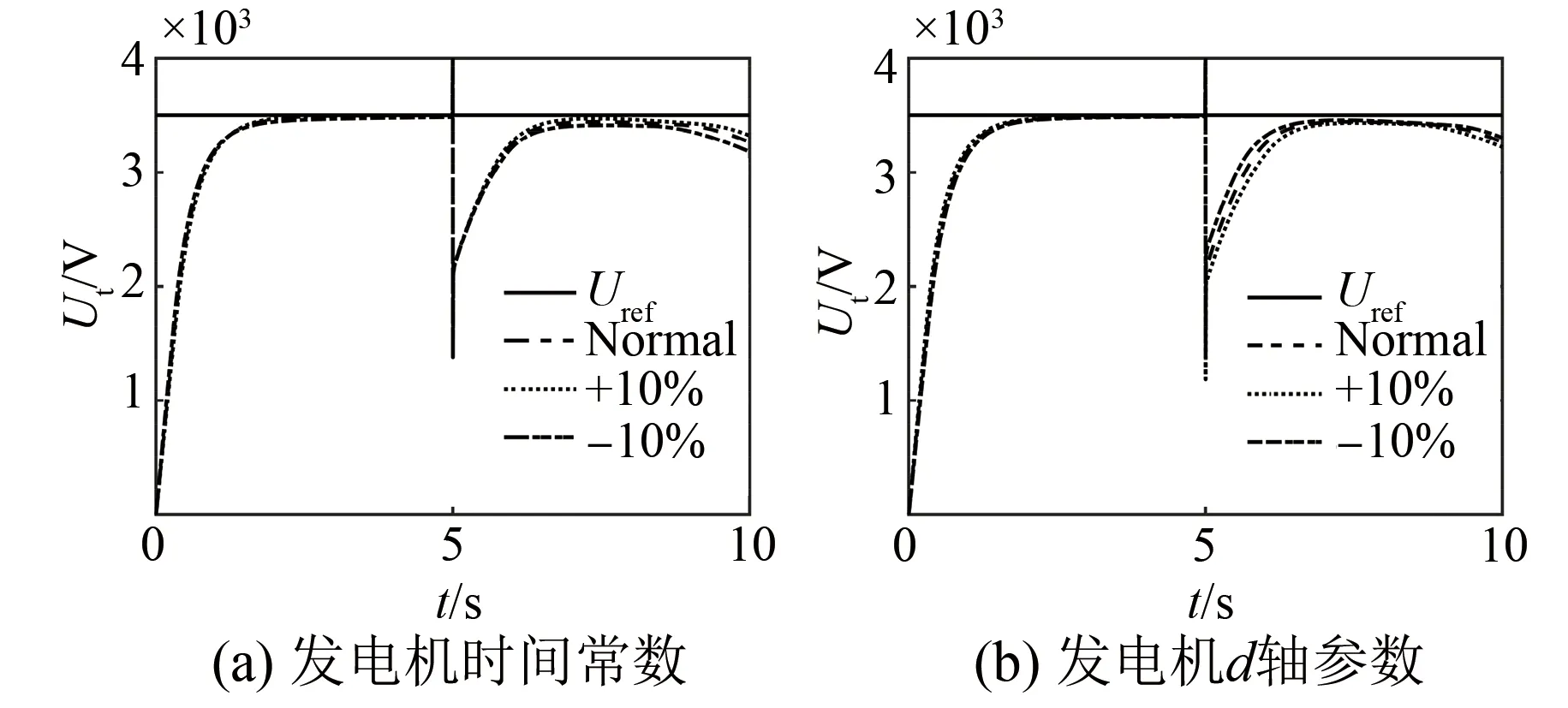
0 (13) 对于WAO-PID的优化,其不等式约束为 0 (14) 2.2.3 优化结果 优化结果如图4和表1所示。 图4 WOA优化结果 表1 优化结果参数 (1) 当误差较大时,为了快速减小稳态误差,使用了较大的比例系数和积分系数,较大的积分系数会使积分器快速进入深度饱和,从而使控制器的输出为最大值或者最小值,只有当积分器退饱和之后,控制器才能重新发挥调节控制的作用。在使用较大的积分系数时防止积分器进入饱和,采用抗饱和积分环节。抗饱和积分环节通过在积分环节中减去过饱和量,当积分器的积分值超过控制器输出的最大或最小限制时,减去的饱和量使积分器快速退饱和,从而抑制积分环节进入饱和状态。 (2) 从式(1)可以看出,负载电流也是系统的扰动,所以为了提高对负载电流的响应速度,在控制器中引入负载电流作为补偿。 (3) 由于控制规律以暂态电动势作为反馈量和给定量,而暂态电动势的计算需要负载电流和发电机的参数,这些数据较难获取而且与发电机通过电机试验获得的试验参数与运行参数有一定的差距,这些参数一定程度上会影响到控制器的性能,此外过于复杂的运算还会使计算速率下降,降低控制器的实时性,因此只用Ut/ωr来代表暂态电动势,这样一方面极大简化了计算,而且也在控制信号中直接反映了脉冲发电机的转速变化。 结合以上三点,最后得出的控制器结构如图5所示。 图5 自适应PID励磁控制方法 为了验证本文所提方法的有效性,以一台300 MVA的脉冲发电机带阻感负载模型进行仿真,系统参数如表2所示。 表2 仿真系统参数 设置发电机的初始转速为500 r/min。 图6为脉冲发电机空载起励的阶跃响应,在t=0时突加给定。可以看出WOA-PID和WOA-自适应PID均可以实现无静差调节,但是WOA-自适应PID的响应速度明显高于WOA-PID。空载起励阶跃响应的时域性能指标如表3所示。 图6 空载起励仿真结果 表3 空载起动性能指标 脉冲发电机有两种带负载的方式,一种是发电机带负载起励,起励过程中负载电流逐渐上升;另一种是发电机经过励磁阶段是机端电压达到额定值之后,再将负载投入,负载电流瞬间上升为较大值。为模拟脉冲发电机的工作情况,下面分别仿真重载起励和空载起励后突加负载。 (1) 重载起励。脉冲发电机带负载起励,在t=0时突加给定。图7(a)WOA-自适应PID在2 s左右时以及接近给定值并趋于稳定,而WOA-PID在3 s时才趋于稳定,另外WOA-自适应PID的稳态误差明显小于WOA-PID的稳态误差。图7(b)中,两种控制方法均会产生超过额定输出的控制电压,原因是引入了负载电流补偿;WOA-自适应PID的控制方法额定输出的保持时间要长于WOA-PID,机端电压在误差较大时有更好的响应速度。图7(c)为发电机的输出电流,即使发电机的机端电压趋于稳定,但是输出电流明显有一个呈上升增大的趋势,原因是发电机转速的下降使负载以及发电机的电抗减小。重载起励阶跃响应如表4所示。 图7 重载起励阶跃响应 表4 重载起励阶跃响应时域性能指标 (2) 突加负载。图8为发电机空载起励,在t=1 s时突加负载的仿真结果。可以看出由于负载的接入,输出电流突然增大使发电机的机端电压严重下降,出现了较大的误差,从图8(b)可以看出,该误差在有电流补偿的情况下,WOA-PID并未使控制电压达到额定输出,而WOA-自适应PID达到了额定输出并较好地维持了一定的时间,使得机端电压有较快的上升速率。 图8 突加负载机端电压恢复 为了验证所提控制方法的鲁棒性能,以发电机参数变化进行仿真,图9(a)为发电机时间常数分别是标称值、110%标称值、90%标准值时,空载起励后在t=5 s突加负载,发电机端电压的波形对比。图9(b)为发电机的d轴参数分别增加10%和减小10%的对比情况。可以看出当参数改变时,脉冲发电机机端电压的变化,与参数为标称值情况下相比具有较好的致性,且误差在合理的范围之内。因此,所提控制方法对发电机的参数具有一定的鲁棒性。 图9 发电机参数扰动 脉冲发电机励磁控制的主要任务是在保证机端电压的稳态误差和响应的快速性。本文提出了参数自适应的PID控制方法,控制器在误差较大时有较大的增益,保证了系统的快速响应;在误差较小时,控制器的增益恢复为较小的值,来保证系统的稳定性。对于引入的多个调节系数,使用WOA来对其进行寻优。最后通过仿真脉冲发电机空载起励、负载起励、突加负载的情况,结果显示自适应PID的效果明显优于传统的PID控制方法:上升时间能够提高为原来的20%以上,负载时的稳态误差也从原来的4%左右降低为2%。稳态误差降低为原来的50%。最后在发电机参数扰动的情况下进行仿真,证明了控制方法对参数扰动具有一定的鲁棒性。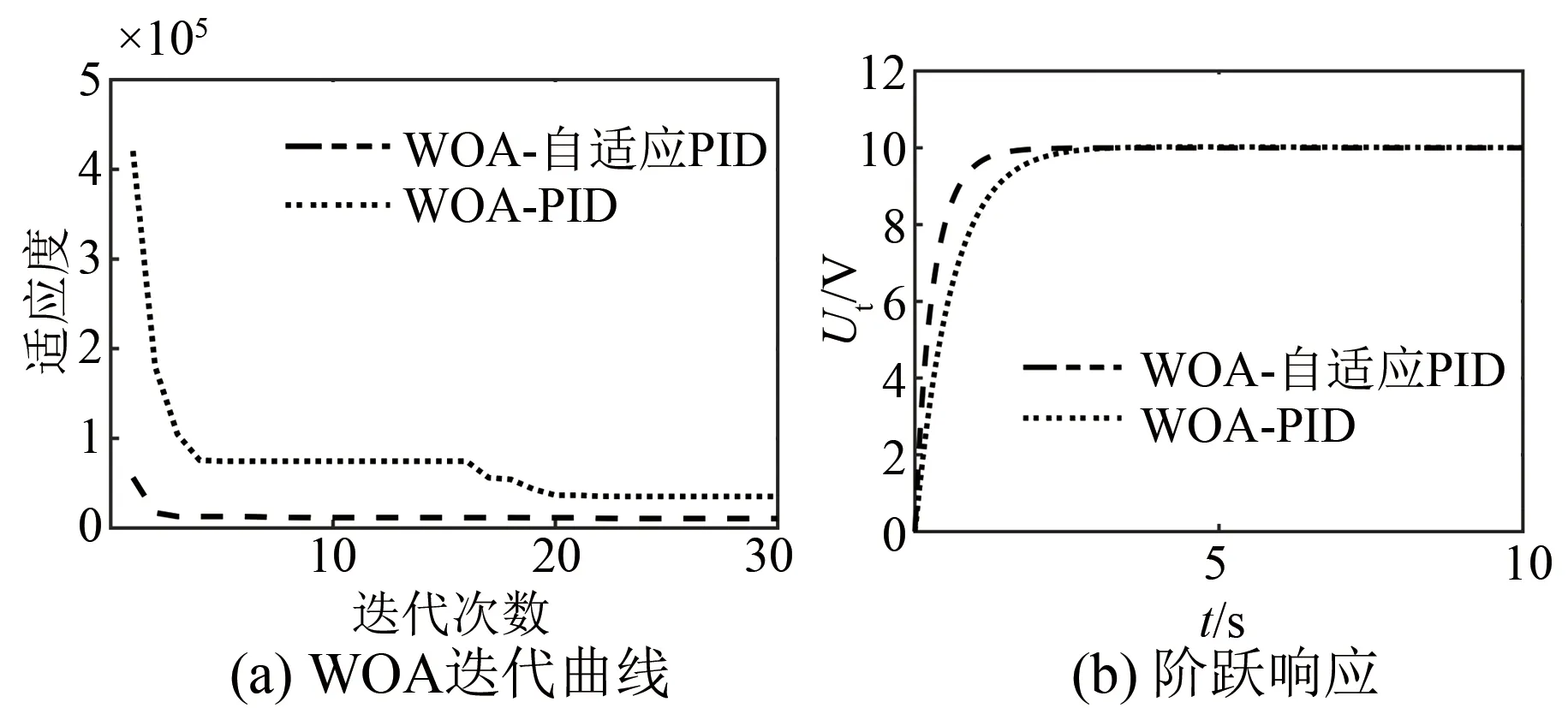
2.3 自适应PID励磁控制
3 仿真结果
3.1 空载试验
3.2 负载试验
3.3 参数扰动
4 结 语

