坡度对土钉支护加固效果的影响研究

摘要：为了探究坡度对土钉加固路堑边坡的支护作用，文章依托某公路路堑开挖工程，通過Midas GTS数值模拟软件，对比研究了75°、63.5°、53°这3种不同边坡坡度条件下的土钉轴力大小变化特征，得出了该种土钉加固方式下的较为合理的路堑边坡坡度。

关键词：深路堑；数值模拟；土钉墙；喷射混凝土；坡率

0引言

土钉加固由于具有施工速度快、施工便捷、成本低廉、加固效果明显（尤其对土质较好的边坡）的优点，在路堑边坡工程设计中受到普遍青睐并在实际工程中得到广泛应用。学者们针对土钉支护方式的加固效果做了大量研究工作，卢敦华等［1］应用应变软化模型针对岩土体材料的特性进行了研究。研究结果表明：应变软化模型结合FLAC 3D软件，能够实现模拟路堑的位移和受力的合理表征。王辉等［2-3］提出了采用稳定性分析的新思路对锚杆复合土钉支护体系受力情况进行了研究。研究结果表明：最小势能法能够计算并有效反映上述支护体系的真实受力状态。郭红仙等［4］针对土钉设置长度对加固后的路堑稳定性的影响问题，采用平衡分析方法进行了深度研究。分析结果表明：在不同地质条件的路堑中，土钉长度根据路堑深度设计成不同的路堑深度比加固效果最佳。孙林娜等［5-6］提出了采用FLAC 3D软件建立三维模型研究支护结构间的协同作用机理。模拟结果表明：不同的墙钉比，支护结构的受力状态各不相同。李浩等［7-8］专门就土钉加固方式中主要设计参数对加固完成后的边坡安全性的影响进行了研究。研究结果表明：朗肯土压力理论能够用于有效了解土钉安设角度以及边坡土的力学特性的相关因素对加固效果进行影响分析。郝明辉等［9］采用Mohr-Coulomb准则研究了如何计算和有效反映土钉对边坡的加固作用。研究结果表明：涉及土钉的相关参数诸如间距、长度等对边坡安全系数有较大影响。

由以上讨论可知：当前针对土钉加固支护方式和土钉和锚杆复合加固支护体系的加固效果研究成果颇多，然而对于路堑边坡坡度带来的对加固效果的影响研究较少。本文依托某公路路堑开挖边坡工程，通过Midas GTS软件建立了路堑边坡的土钉加固支护模型进行二维条件下的土钉支护效果研究，主要通过对比3种不同边坡坡度条件下的土钉轴力大小变化特征，提出了该种土钉加固方式下的较为合理的路堑边坡坡度。

1 工程概况

某公路路线全长3.258 km，二级公路标准，路面宽12 m，两侧各设0.5 m路边石，路基全宽13 m。路面为沥青混凝土路面结构。部分路段需开挖路堑，开挖模型如图1所示，开挖深度为5.8 m，周边有20 kPa的均布荷载分布，采用土钉墙加喷射混凝土支护，土钉设计为20 mmHRB400钢筋。共设计3排土钉，每排土钉长度为5 m，斜向下以15°打入土体中，同时加设预应力抗拉强度为30 MPa。土层自上而下共设有3层，虽均为第四纪粉质黏土，但每个土层的物理力学参数有一定差异，自上而下分别为土层1、土层2、土层3，各土层物理力学参数如表1所示。

2 数值模型的建立

根据上述边坡工程开挖模型采用Midas GTS软件对照进行合理建模，通过网格剖分，将路堑边坡工程模型剖分为7 052个有限单元体，单元节点数共计7 021个。按照表1所示的自上而下的各土层物理力学参数对其各个区域的岩土体材料性质进行参数设置和赋值。

边界条件设置：路堑左右两侧均为固定边界约束，底部也为固定边界约束，上部及路堑开挖深度范围内的土体边坡坡面和底部均为自由约束。其中边坡坡度共设计了75°、63.5°、53°3种工况条件。

3 计算结果分析

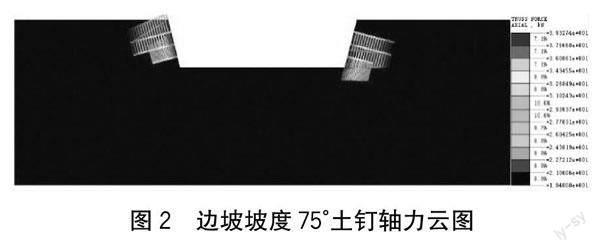
为了对不同边坡坡度条件下的土钉受力特性进行分析，分别进行了75°、63.5°、53°边坡坡度3种工况条件的土钉加固路堑边坡的稳定性求解计算，通过出图操作导出计算的土钉轴力图，得到了75°边坡坡度条件下的土钉加固路堑边坡的土钉轴力变化云图，如图2所示；63.5°边坡坡度条件下的土钉加固边坡的土钉轴力变化云图，如图3所示；53°边坡坡度条件下的土钉加固边坡的土钉轴力变化云图，如图4所示；最后，通过将各排土钉轴力进行统计并绘制了如图5所示的3种坡度条件下的各排土钉的轴力大小分布图。

3.1 路堑边坡为75°

当边坡坡度设置为75°时，通过计算，并绘制相应的轴力变化云图，获得了如图2所示的土钉轴力大小分布变化云图。

由图3可知，路堑边坡坡度为75°条件下第一排土钉最大轴力约为24.4 kN，最大轴力沿土钉长度近似平均分布；第二排土钉的最大轴力约为37.6 kN，最大轴力集中分布于靠近开挖边界的端部；第三排土钉的最大轴力约为39.3 kN，最大轴力同样集中分布于靠近开挖边界的端部并呈现出向深处逐渐变小的趋势，但最大轴力分布范围较第二排土钉更大。

3.2 路堑边坡为63.5°

由图3可知，路堑边坡坡度为63.5°条件下第一排土钉最大轴力约为17.9 kN，最大轴力沿土钉长度近似平均分布；第二排土钉的最大轴力约为30.4 kN，最大轴力集中分布于靠近开挖边界的端部；第三排土钉的最大轴力约为34.1 kN，最大轴力同样集中分布于靠近开挖边界的端部并呈现出向深处逐渐变小的趋势，但最大轴力分布范围较第二排土钉更大。

3.3 路堑边坡为53°

由图4可知，路堑边坡坡度为53°条件下第一排土钉最大轴力约为14.3 kN，最大轴力沿土钉长度近似平均分布；第二排土钉的最大轴力约为27.3 kN，最大轴力集中分布于靠近开挖边界的端部；第三排土钉的最大轴力约为30.1 kN，最大轴力同样集中分布于靠近开挖边界的端部并呈现出向深处逐渐变小的趋势，但最大轴力分布范围较第二排土钉更大。

由上述分析可知：随着路堑边坡坡率的降低，土钉的最大和最小轴向拉力均逐渐减小，将上述各工况每排土钉轴力变化统计，绘制出如图5所示的各排土钉轴力随边坡坡度变化曲线图。

由图5（a）可知，第一排土钉的最大、最小轴力均随着路堑边坡逐渐趋缓而变小，而图5（b）、5（c）中的第二、三排土钉最大、最小轴力随着路堑边坡坡度减小呈逐渐变小的特征。相对于坡度为75°边坡，63.5°边坡的第一排土钉最大轴力降低了约11.6%，第二排土钉的最大轴力降低了约15.4%，第三排土钉的最大轴力降低了约14.3%；53°边坡的第一排土钉最大轴力降低了约19.5%，第二排土钉的最大轴力降低了约20.3%，第三排土钉的最大轴力降低了约50.4%。3种工况下土钉抗拉强度利用率（轴向拉应力/0.7倍抗拉强度设计值）依次为：49.7%、43.1%、39.2%。

4 结语

本文依托某公路路堑开挖边坡工程，通过Midas GTS软件进行了不同边坡坡度条件下的土钉轴力分布变化分析，得到如下结论：

（1）各坡度条件下，第一排土钉最大轴力均为最小，且最大轴力沿土钉长度近似均匀分布；第二排、第三排土钉最大轴力集中分布于靠近开挖边界的端部，向深处逐渐变小的趋势。

（2）相对于坡度为75°，63.5°边坡的土钉最大轴力降低幅度自第一排至第三排逐渐增大；53°边坡各排土钉最大轴力降低了约19.5%，第二排土釘的最大轴力降低了约20.3%，第三排土钉的最大轴力降低了约50.4%，降低幅度最大。

（3）3种工况下土钉抗拉强度利用率（轴向拉应力/0.7倍抗拉强度设计值）依次为：49.7%、43.1%、39.2%。均满足规范要求。实际工程中可根据场地要求进行边坡开挖的坡度设计。

参考文献：

［1］卢敦华，王星华.基于应变软化模型的深基坑土钉加固分析［J］.解放军理工大学学报（自然科学版），2009，10（1）：61-66.

［2］王 辉，赵 雪，程建华.考虑钉锚耦合的支护体系最小势能分析［J］.广西大学学报（自然科学版），2021，46（2）：253-258.

［3］王丽萍，张 嘎，张建民，等.土钉加固黏性土坡动力离心模型试验研究［J］.岩石力学与工程学报，2009，28（6）：1 226-1 230.

［4］郭红仙，周 鼎.软土中基坑土钉支护稳定性问题探讨［J］.岩土力学，2018，39（S2）：398-404.

［5］孙林娜，徐福宾.水泥土墙复合土钉墙的协同作用机理数值模拟［J］.华侨大学学报（自然科学版），2020，41（3）：314-322.

［6］黎永索，林 杭.土钉与土体相互作用的仿真试验分析［J］.中国地质灾害与防治学报，2008（2）：76-79，113.

［7］李 浩，白海波，韩立军，等.土钉安设位置与角度对边坡加固效果影响分析［J］.地下空间与工程学报，2016，12（2）：496-502.

［8］李朝方，龙凤华.土钉在河道老旧岸墙补强加固中的应用［J］.水利技术监督，2021（1）：108-112.

［9］郝明辉，张 红，彭 涛，等.土钉加固边坡稳定性分析的等效参数提高方法［J］.水利与建筑工程学报，2014，12（4）：32-37.

作者简介：赵东戈（1988—），工程师，研究方向：公路桥梁养护工程。