基于可控卷积曲面的三维神经元建模

朱晓强，陈 琦

（上海大学 通信与信息工程学院，上海 200444）

0 概述

自现代神经科学诞生以来，深入认识神经元形态是神经科学领域重要的研究方向之一。大脑的复杂结构使得密集神经网络特征和行为过程的分析变得极为困难。三维可视化已被证明是评估复杂神经系统的有效工具。

GLASER 等［1］提出Neurolucida 软件应用，使用锥形圆柱体表示神经元节段，在分支点处通过球体将神经元节段相连接，生成的网格模型在段之间是不连续的，不满足水密性的特点。NeuGen［2］、GENESIS［3］等软件应用可以生成神经元模型表面，但均使用球体表示胞体，生成的体细胞网格质量较差。AGUIAR 等［4］开发Py3DN 工具箱，通过几何近似的方法实现更真实的躯体重建，但没有将生成的细胞体与树突相连接。LASSERRE 等［5］研究用于电生理仿真的皮层神经元的重建，提出从一组采样神经元形态数据中生成一个连续的表示神经元膜表面的算法，但代码难以复现，因分支上存在尖锐的边缘，导致重建网格的质量较差。

BRITO 等［6］提出使用Neuronize 工具构建神经元细胞三维模型，主要使用胡克定律和质量弹簧模型在合理的物理基础上重建神经元的胞体模型，但与GLASER［1］相似都采用圆柱体表示神经元节段，改进之处是使用剪切和拼接的方式连接神经元段与段、段与胞体之间的缝隙。GARCIA-CANTERO等［7］在Neuronize 的基础上提出NeuroTessMesh 硬件加速工具，能够解决复杂场景下存储和计算成本较高的问题，以生成具有自适应动态细化功能的神经元网格模型，但是该工具生成的网格在分支处不平滑且不满足水密性要求。

ABDELLAH 等［8］提出从新皮层神经元电路的形态骨架重建规模较大且高度详细体积模型的新方法。通过对单个神经元形态数据进行预处理，从预处理后的神经元形态骨架创建分段平滑和符合水密性要求的网格模型，然后构造局部体积模型，最后合并成全局体积模型，其缺点在于网格是分段水密的。

文献［9-11］提出用于反映扩散模拟的四面体体积模型，其网格满足水密性和双流形的特点。由于该体积模型具有较高的镶嵌性且忽略神经元形态的真实有机外观，因此不能用于交互式可视化分析。

ABDELLAH 等［12］提出使用Skin Modifiers 从神经元的形态骨架生成高保真的新皮层神经元表面网格。KARLSSON 等［13］基于符号距离函数和光线追踪［14］技术，提出用于渲染大规模神经元电路数据的高保真可视化方法，但是生成网格的质量不高且不平滑。

为生成高质量、平滑且满足水密性要求的三维神经元网格模型，本文提出一种三维神经元建模方法。通过预处理NeuroMorpho.Org 数据库提供的神经元形态数据，对现有基于骨架的卷积曲面混合建模方法进行改进，设计一种基于可变支撑半径控制的卷积曲面混合新方法。利用稀疏体素结构提高分辨率并加快等值面提取过程，以优化网格生成的神经元三角网格模型和体积模型。

1 神经元数据预处理

从NeuroMorpho.Org 数据库中获取的SWC 格式神经元形态数据以ASCII 形式进行编码，每个非空行代表一个神经元样本点，其中包含七个数据项，具体如表1 所示。其中：采样号和父采样号表示空间中样本点的父子连接关系；结构标识符主要包括0-未定义、1-胞体、2-轴突、3-树突和4-尖端树突5 种类型；X、Y、Z是以μm 为单位的空间坐标；半径是树突厚度的1/2，单位是μm。

表1 标准神经元数据结构Table 1 Structure of standard neuron data

原始神经元数据存在非常短的神经元骨架节段以及不规则的顶点采样密度。此外，数据还可能存在潜在异常采样点和分支，如果直接构建网格模型会导致网格不连续、拓扑异常和分支重叠，因此，需要对神经元数据进行预处理。

神经元节段线骨架示意图如图1 所示。对于线骨架Si，PA、PB分别是左右两端采样点，rA、rB分别是采样点的半径，lAB是线骨架的长度，引入可变参数e，如果lAB≤e×Max(rA，rB)，其中e≥2，则定义Si为短边。

图1 神经元节段线骨架示意图Fig.1 Schematic diagram of neuron segmental line skeleton

由于短边现象几乎存在于所有的神经元形态数据中，因此针对采样点属于不同类型的拓扑角色，提出以下预处理算法流程：

输入SWC 格式神经元数据

输出去除异常采样点和短边后的神经元数据

步骤1定义U为已访问过的节点集合，依次遍历节点，删除节点半径值为负数的样本点，并连接前后节点。

步骤2移除长度接近0（小于1e-4）的分支。

步骤3处理短边问题，如果PA、PB都是内部点，首先获取PA的父节点P0，然后连接P0和PB，最后删除PA节点。

步骤4如果PA是内部点，PB是分支结束点，处理方法同步骤3。

步骤5如果PA是分支点，PB是内部点，由于删除分支点会破坏整体拓扑结构，则首先获取PB的子节点PC，然后连接PA和PC，最后删除PB节点。

步骤6如果PA是分支点，PB是分支结束点，直接删除PB。

步骤7如果PA是根节点，PB是其他节点，处理方法同步骤5。

步骤8根据集合U，删除单个分离的神经元分支。

以人类大脑区域的神经元电路数据为例，三维神经元预处理结果如图2 所示。原始神经元数据包含1 429 个采样点，预处理后的神经元数据包含1 374 个采样点。预处理算法能有效地解决神经元形态数据可能存在的异常样本点、短边等问题，减少采样点数量，为后续网格模型的生成提供有效的输入数据。

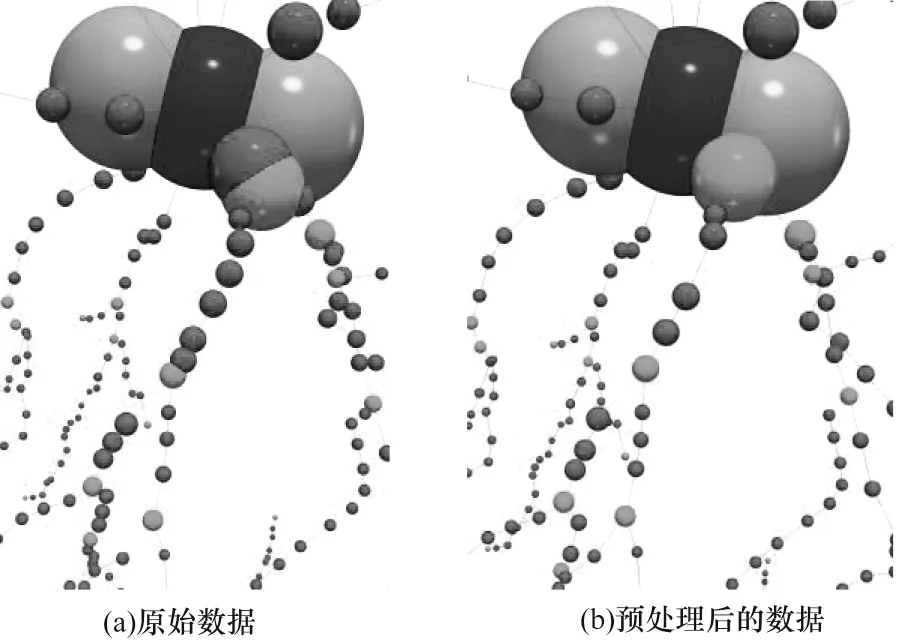
图2 三维神经元预处理结果Fig.2 Preprocessing result of 3D neuron

2 三维神经元建模

2.1 卷积曲面

卷积曲面最初被定义为由几何骨架和高斯核函数的卷积生成的［15］，其数学定义如式（1）所示：

其中：λi为第i段几何骨架的权重值；Fi(x，y，z)为第i段几何骨架的势能函数；参数T为提取等值面的阈值。

根据式（1），假设p为三维空间中的点，S为几何骨架，骨架的几何函数可定义为：

对于一个核函数f，且三维空间点q∈S，几何骨架S在点p处的总势能值可定义为：

核函数按作用范围分为无限支撑和有限支撑核函数。对于无限支撑核函数，定义域内所有的势能值均大于零，例如高斯函数［15］和柯西函数［16］。对于有限支撑核函数，在指定的定义域内有值，在其余范围内的势能值均为零，例如Metaballs［17］。采用无限支撑核函数构造卷积曲面有两个缺点：1）在构造单个神经元骨架模型时，因卷积场计算过远导致生成曲面效率低；2）当曲面混合时，一旦势能函数发生变化，须重新计算整个骨架的势能场，无法做到局部控制。鉴于此，本文参考JIN 等［18］提出的方法使用四次多项式作为卷积核函数，如式（4）所示：

其中：R为核函数的有效支撑半径，用于剪切离目标太远的骨架，可有效控制混合范围。

2.2 卷积曲面可控混合

基于ZHU 等［19］提出的结论，对于一条线骨架Si，如果曲面厚度为di，则p点处的权重值λi满足如下关系：

为方便控制局部混合，本文引入比例参数t=Ri/di，其中，Ri为支撑半径。对于常规卷积曲面，di和Ri的默认关系为di=Ri/2，即t=2。根据式（5）求得λi为：

通过改变参数t的值来改变空间每个位置相对骨架的权重值，从而改变基于骨架的卷积曲面混合程度。单纯改变t虽然可调节混合程度，但是无法做到局部混合。本文根据线性插值的思想来局部调节线骨架上某一段的支撑半径值，提出一种基于可变支撑半径控制的卷积曲面混合新方法。基于可变支撑半径变化的卷积曲面示意图如图3 所示。

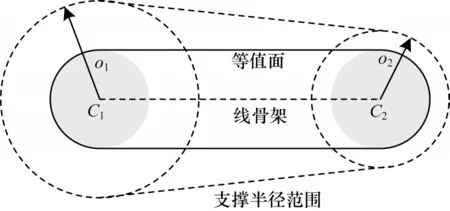
图3 基于可变支撑半径变化的卷积曲面示意图Fig.3 Schematic diagram of convolution surface based on variable support radius change

假设线骨架Si的左端点C1处的有限支撑半径为o1，右端点C2处的有限支撑半径为o2，l10为C1C0的长度，l12为C1C2的长度，则在线骨架之间任一点C0处的有限支撑半径可定义为：

当线骨架混合时，通过为每一段线骨架设置不同的左右端点支撑半径，实现局部混合的目的。

因卷积曲面的叠加性，在线骨架段之间自动混合生成光滑连续的表面，但是在多段线骨架之间会因势能值的不断叠加而产生额外的“鼓包”现象。利用上述方法可有效地缓解“鼓包”问题以及解决常规卷积曲面因支撑半径范围过大而产生的过渡混合问题。

2.3 稀疏体素结构

在上节中，本文将三维神经元骨架作为输入数据，并基于卷积曲面生成三维空间离散势能场，利用经典的Marching Cubes 算法［20］提取等值面，但在实际计算中可能会产生问题。基于Marching Cubes 算法的等值面提取示意图如图4 所示。假设在每个体素边长为1 的多个立方体中计算一条曲面厚度为1，支撑半径为1.2 的线骨架的卷积曲面，当使用Marching Cubes 算法提取等值面时，等值面和支撑半径可能会处于同一个体素中，导致最终无法有效提取高质量的神经元网格模型。

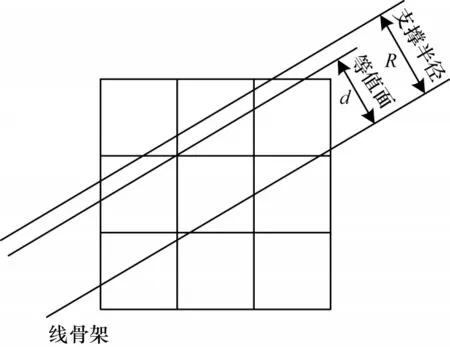
图4 基于Marching Cubes 算法的等值面提取示意图Fig.4 Schematic diagram of isosurface extraction based on Marching Cubes algorithm

通过提高体素分辨率的方法，使同一个体素内只包含等值面和支撑半径就可解决上述问题，但密集网格在构造多个模型实例时，其内存占用随模型体积的增大而增大。由于三维神经元复杂的分支结构，空间中存在大量的空隙，因此不需要在一个密集的网格中均匀采样数据，可采用稀疏的体积数据结构来提高效率。

本文参考MUSETH［21］提出的基于VDB 的稀疏体素结构，该结构具有内存效率高、支持时变数据模拟、自适应采样等特点。核心思想是在一个类似B+树的多层次数据结构中动态地安排网格处的体素块，将空间分为根节点、两个内部节点和一个叶子节点三部分。其中，最小的体元素按活跃值可分为活跃体素和非活跃体素，且每一个活跃体素都有一个区别于背景值的默认值。

针对分辨率较低的问题，本文通过改变体素大小来解决，设置默认背景值为0，活跃体素值为0.5，利用上述稀疏体素结构计算三维空间卷积势能场，以加快等值面提取速度。

2.4 网格后处理

2.4.1 网格重构

基于稀疏体素结构生成的神经元模型网格顶点分布不均匀，会影响基于网格的数值模拟实验等应用。因此，本文需要重构并均匀化网格且均匀的网格必须满足三个基本条件：所有边等长、所有三角形面积相等和所有顶点度数为60°。

本文参考BOTSCH等［22］提出的Isotropic Remeshing网格优化算法，设定一个目标边长L，遍历网格中所有边长向目标边长靠近，得到最终优化结果。具体处理步骤如下：1）分割所有长度大于4L/3 的边；2）坍缩所有长度小于4L/5 的边；3）翻转所有边以优化度数；4）将所有新加入的点映射到切平面。

为有效地生成体网格数据，本文利用MeshLab［23］工具验证三维神经元网格模型的水密性，使其不存在非流形边和顶点。

2.4.2 网格细分

为获得表面更加光滑且包含更多细节信息的三维神经元网格模型，本文采用Loop［24］算法对重构后的网格做进一步细分处理。细分过程主要包括计算边点和更新原始点两个过程。

在计算边点的 过程中，假设四个点V0、V1、V2、V3，其拓扑关系如图5 所示。

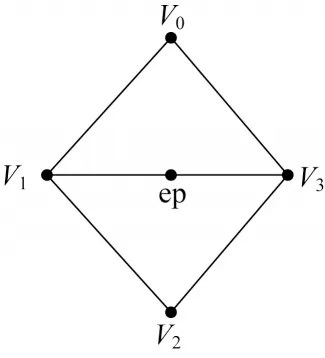
图5 计算边点的示意图Fig.5 Schematic diagram of calculating edge point

针对由属于两个三角面的每条边所组成的四点面，面点fp 为：

每条边的中点ec 为：

fp 与ec 点的平均点，即边点ep 为：

其中：eep表示该边属于两个三角面片，即边点处于网格内部。当边点位于网格边界时，边点直接退化为中点。

之后，更新原始点，设v为原始点，则更新后的点v'为：

2.4.3 网格体素化

为生成能在脑神经元组织中进行光传播模拟实验的神经元模型，本文利用TetGen［25］软件生成高质量的神经元四面体体积模型。TetGen 体素化过程如图6 所示。

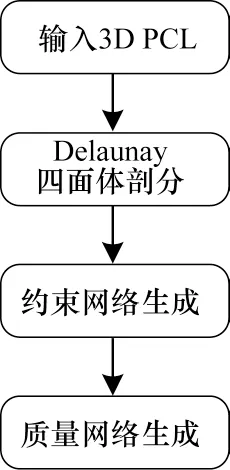
图6 TetGen 体素化流程Fig.6 Procedure of TetGen voxelization

首先，将细化后的三维神经元网格作为输入数据；然后，类比二维Delaunay 三角剖分，在三维空间中对神经元网格模型进行四面体剖分，生成保持原有神经元模型形态的约束网格；最后，通过限制插入模型内顶点个数以及四面体体积来生成高质量的三维神经元体积模型。

3 实验结果与分析

3.1 建模结果分析

为验证本文提出的基于可控卷积曲面的三维神经元建模方法的有效性，将第1 节中的神经元形态骨架作为输入数据，并与ABDELLAH 等［8］、ABDELLAH 等［12］及KARLSSON 等［13］所提方法的建模结果进行对比。

不同方法的三维神经元建模结果对比如图7 所示。文献［8］所提的方法生成的神经元网格是分段水密的，在细胞体与分支之间会出现断层，即整体网格不满足水密性要求，且在分支处曲面不平滑，易产生折痕现象。文献［12］所提的方法相较于文献［8］生成的神经元网格曲面更加平滑，但对于复杂神经元骨架易生成不满足整体水密性的光滑网格模型，且在多个骨架相交处易生成异常拓扑结构。上述两种方法的额外贡献点在于利用网格变形技术构造细胞体的结构。文献［13］利用平滑函数解决神经元分支处的折痕现象，但产生额外的曲面鼓包现象。本文根据卷积曲面的叠加性质直接混合生成神经元结构模型。相较于前三种方法，本文方法生成的网格模型整体呈光滑连续，能够更加真实地描绘三维神经元形态。

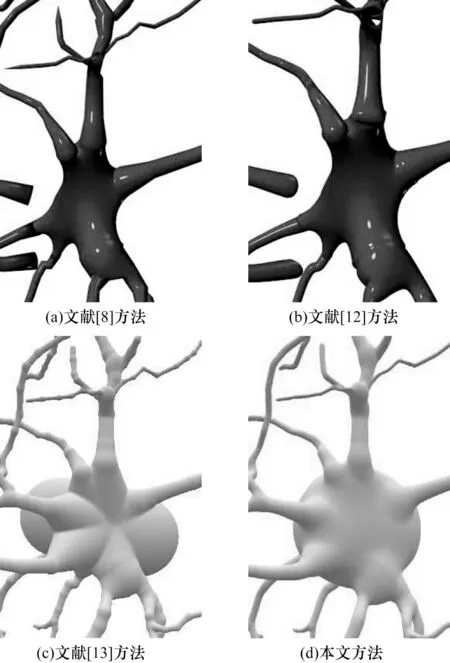
图7 不同方法的三维神经元建模结果对比Fig.7 3D neuron modeling results comparison among different methods

由于神经元形态骨架极其复杂，存在骨架之间距离较近的情况，因此可能会出现曲面相交的问题，影响基于网格的数值模拟等应用。不同方法的近距离骨架建模结果对比如图8 所示。文献［8，12-13］都没有提出有效的方法解决曲面相交问题。本文利用2.2 节中提出的基于局部可变支撑半径控制的卷积曲面混合新方法来控制曲面混合程度，将过渡混合处的骨架支撑半径和曲面厚度的比例系数t设置为1.2～2.0 之间动态线性插值，有效解决曲面相交问题，结果如图8（d）所示。

图8 不同方法的近距离骨架建模结果对比Fig.8 Short-range skeleton modeling results comparison among different methods

在线骨架厚度较小的位置，卷积曲面无法提取等值面或生成的网格质量较差，本文利用稀疏体素结构改变体素值的大小来提高分辨率，结果如图9所示。随着体素值的减小，生成的曲面越光滑，相应的时耗也逐渐增加。

图9 基于稀疏体素结构的卷积曲面Fig.9 Convolution surface based on sparse voxels structure

为进一步说明本文方法的高效性，在搭载AMD Ryzen7-5800H（3.20 GHz）处理器、16 GB 内存、Ryzen 集成显卡的win11 电脑设备和Visual Studio 2019 平台上，不同方法构建神经元网格模型所需的时间对比结果如表2 所示。其中，Z1表示分辨率574×1 054×208 像素，Z2表示分辨率1 437×2 635×522 像素。在相同分辨率下，文献［12］所提的方法解决了文献［8］所提方法存在的分支处不平滑问题，但平均时耗增加约130%；文献［13］所提的方法相较于文献［12］，在解决分支折痕问题的同时将平均时耗减少了约50%，但是在分支处产生额外鼓包问题；本文方法不仅能有效平滑分支处曲面，而且提供参数来控制曲面混合程度，以避免出现异常拓扑，建模速度相较于文献［13］方法提升了约1.5 倍。

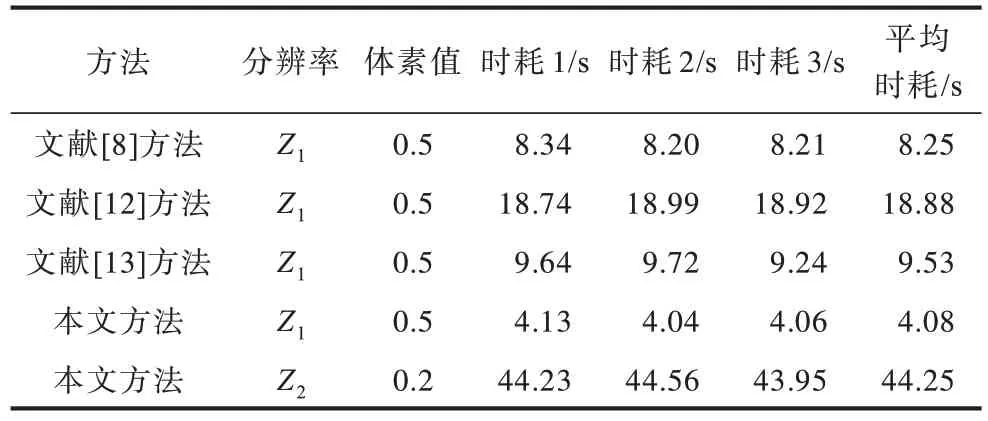
表2 不同方法构建三维神经元模型的时耗对比Table 2 Time consumption of constructing 3D neuron model comparison among different methods

3.2 网格后处理分析

为获得更高质量的三维神经元网格模型数据，本文进行一系列的网格后处理操作包括网格重构、网格细化和网格体素化，结果如图10 所示。初始网格模型局部如图10（a）所示，重构后的网格局部如图10（b）所示，细化后的网格局部如图10（c）所示，优化后的网格顶点分布更加均匀且表面更加光滑。

图10 三维神经元网格模型优化结果Fig.10 Optimization results of 3D neuron grid model

为获得用于光学实验的高质量体积模型，本文使用MeshLab 软件验证三角形网格的水密性，将.ply格式的网格数据作为输入，利用TetGen 软件直接生成，结果如图11 所示。本文方法在保持神经元形态的前提下，在网格内部生成了等体积密集的四面体网格。

图11 三维神经元网格体素化Fig.11 Grid voxelization of 3D neuron

4 结束语

针对生成表面网格的光滑度和网格分支处的平滑度问题，结合卷积曲面技术与线性插值思想，本文提出可控卷积曲面混合方法，用于构造三维神经元模型。采用稀疏体素技术加快网格生成速度，解决模型生成效率的问题。与现有神经元建模方法相比，本文方法具有较优的鲁棒性和高效性。下一步将研究复杂神经元骨架数据产生的环状结构问题，实现高质量神经元数据的建模。