基于邻域聚合与CNN 的知识图谱实体类型补全

邹长龙，安敬民，李冠宇

（大连海事大学 信息科学技术学院，辽宁 大连 116026）

0 概述

知识图谱通常以RDF 三元组的形式陈述一条事实［1］，表示为(e1，r，e2)，其 中e1和e2为知识图谱的实体，r为e1和e2之间的关系，例如，（Jackie Chan，Isborn，Hong Kong）。在知识图谱中除三元组之外，还有大量的实体类型实例（实体-实体类型元组）［2］，记为(e，t)。例如，（Jackie Chan，Actor）表示实体“Jackie Chan”的类型为“Actor”。知识图谱中的实体类型信息可以用于各种下游任务，例如实体对齐［3］、实体链接［4］、知识图谱补全［5-6］等。实体类型信息的缺失会影响这些算法的有效性与准确性，但知识图谱在实体类型信息方面经常存在信息不完整问题。

知识图谱实体类型信息不完整的问题可以通过实体类型补全（推断实体e的类型t）来解决。知识图谱实体类型补全是知识图谱补全的子问题。早期的知识图谱实体类型补全模型主要以概率分布为基础［7］。表示学习现已成为知识图谱相关研究的基础。对于知识图谱，表示学习［8］是通过机器学习等方法学习知识图谱中对象的低维嵌入向量表示，学习到的嵌入向量不仅可以保留知识图谱中对象蕴含的语义信息，而且用于各种基于知识图谱的下游任务，例如知识图谱补全［6］、推荐系统［9-10］。因此，表示学习技术通常被用于知识图谱实体类型补全。

大多数基于表示学习的实体类型补全模型倾向于对实体-实体类型元组(e，t)进行建模和实体类型补全，而没有有效地利用关系。例如RESCAL-ET［10］、HOLE-ET［10］、TransE-ET［10］、ETE［10］等模型使用异步的方式学习实体、关系和实体类型，并进行嵌入表示。虽然这些模型学习了关系的嵌入表示，但是关系嵌入中包含的信息在进行实体类型补全时并没有被使用。ConnectE［11］模型使用三元组、实体-实体类型元组和实体类型三元组进行训练和实体类型补全。尽管ConnectE 通过实体类型三元组利用了关系，但实体类型三元组造成了测试集数据的泄露。这些模型的建模方法无法有效地利用知识图谱三元组，特别是实体之间关系包含的信息。然而，三元组中关系的信息有助于推断一个实体的所属类型。例如：对于三元组（Chicago，Islocation，Illinois）和（Chicago，Iswriter，Rob Marshall），关 系“Islocation”和“Iswriter”的信息有助于推断出实体“Chicago”的类型可能包括“City”和“Film”。同时，这些模型属于距离模型（使用向量的L1 或L2 范数衡量实体和实体类型的相似性）生成特征的数量有限，导致模型表达能力不足。卷积神经网络（Convolutional Neural Network，CNN）用于学习嵌入的深层表达特征，在不增加嵌入维度的基础上增强模型的表达能力［12］。

本文提出一种基于邻域聚合与CNN 的知识图谱实体类型补全模型NACE2T，使用编码器-解码器的结构。编码器利用注意力机制为实体邻域中的每个关系-实体对分配权重，以聚合实体邻域中的实体和关系包含的信息，达到利用知识图谱三元组或实体之间关系的目的。此外，考虑到现有实体类型补全模型的表达能力有限，基于CNN 提出一个知识图谱实体类型补全模型CE2T 作为解码器，衡量编码器输出的实体嵌入和实体类型嵌入之间的相似性。

1 相关工作

文献［13］利用领域知识和知识图谱外部的文本数据进行知识图谱实体类型补全，并提出一个基于张量分解的模型。文献［14］利用文本数据进行实体类型补全，并提出一种基于神经网络的实体类型补全模型。本文主要使用知识图谱的内部数据（三元组和实体类型实例）进行实体类型补全。

对于知识图谱，表示学习技术［1，15］主要集中在学习实体和关系的嵌入向量表示［16-18］，对编码实体-实体类型元组和三元组学习实体、关系和实体类型嵌入表示的较少。因此，本文主要介绍对三元组和实体-实体类型元组(e，t)进行建模的实体类型补全模型。

文献［10］提出的实体类型补全方法采用异步的方式学习实体、关系和实体类型的嵌入向量。首先，使用知识图谱补全方法，如TransE［15］、RESCAL［16］、HOLE［17］和ContE［18］学习实体 的嵌入向 量e，目 的是让实体在向量空间中根据它们的类型进行聚类，在实体的周围嵌入类型；其次，在训练时保持实体的嵌入向量e不变，通过最小化实体嵌入向量e与实体类型嵌入向量t之间的距离来更新实体类型的嵌入向量t，称 为TransE-ET、RESCAL-ET、HOLE-ET 和ETE。它们的评分函数ϕ(e，t)=||e-t||L1，其中||x||L1表示向量的L1 范数。虽然这些方法在训练过程中利用实体之间的关系，但是在进行实体类型补全时未利用关系蕴含的信息。

文献［11］构建的最新实体类型补全模型是ConnectE，提出实体嵌入和实体类型嵌入应处于不同的向量空间。同时，ConnectE 为利用实体之间的关系，根据知识图谱三元组引进实体类型三元组。然而，实体类型三元组的创建方式没有考虑到实体与不同的关系组合会表现出不同的语义［19］。此外，实体类型三元组导致测试集数据出现了泄露。ConnectE 的评分函数ϕ(e，t)=||M·e-t||L2，其 中||x||L2表示向量的L2 范 数。ConnectE 同样采用异步的方式进行训练，其训练过程分为三个阶段：1）使用TransE［15］训练实体嵌入和关系嵌入；2）训练实体类型嵌入和将实体嵌入从实体空间投影到实体类型空间的投影矩阵M；3）使用TransE 训练实体类型三元组，并且只改变关系的嵌入，实体类型嵌入保持不变。

虽然上述模型在尝试进行知识图谱实体类型补全时利用关系，但是它们利用关系的方式都是采用异步的方式去学习实体、关系和实体类型的嵌入表示，导致时间开销增大。本文提出的NACE2T 模型采用同步的训练方式，即同时学习实体、关系和实体类型的嵌入表示。

2 NACE2T 模型

NACE2T 模型采用编码器-解码器的结构。编码器为基于注意力机制的邻域聚合器，用于利用知识图谱中实体之间的关系。解码器为基于CNN 设计的知识图谱实体类型补全模型CE2T。NACE2T模型架构如图1 所示。

图1 NACE2T 模型架构Fig.1 Framework of NACE2T model

2.1 编码器

对于一个三元组(ei，rk，ej)，其嵌入向量分别为ei∈Rd，ej∈Rd和rk∈Rd。当使用聚合器聚合实体ei邻域中的信息时，生成ei新的嵌入表示为：

其中：Agg 表示聚合器；N(ei)表示实体ei的一跳邻域；W1∈Rd×d1和W2∈Rd×d1表示线性变换矩阵；σ(·)表示非线性激活函数。

在知识图谱中的实体之间通常存在一条含有丰富语义信息的关系，然而，式（1）在聚合过程中忽略关系，因此并不适用于知识图谱。为了在进行实体类型补全时利用实体之间的关系，本文的编码器需要在聚合实体邻域信息的过程中聚合关系的信息，因此，在聚合信息的过程中利用消息传播机制［20］对实体和关系的嵌入进行组合运算，形式为Rd×Rd→Rd。在此情况下，ei新的嵌入表示为：

其中：Riu表示链接实体ei与N(ei)中包含的实体关系集合；φ(·，·)表示组合运算；φ(u，r)表示实体u通过关系r到实体ei的消息。

聚合器Agg 的选择有很多种，最常用的是图卷积网络（Graph Convolutional Network，GCN）［21］聚合器。但是GCN 在聚合信息的过程中会平等对待实体之间的边或关系，即无差别地聚合实体邻域中的信息［22］，而实体邻域中的某些信息可能对推断实体所属的类型没有作用。该问题可以通过注意力机制来解决。同时，GCN 属于直推式的图神经网络，无法使用mini batch 的思想来训练。为了使用mini batch 的思想来训练模型，本文的编码器在实体的一跳邻域中利用抽样方法随机选取固定数量的关系-实体对来聚合信息。

一般的注意力计算方法都是对知识图谱中的实体和实体计算注意力［23］，但是这种计算方法同样会忽略实体之间的关系。为了在计算注意力时利用关系的信息，本文的编码器对实体和关系-实体对计算注意力，或对实体和消息φ(u，r)计算注意力。

给定一个三元组(ei，rk，ej)，实 体ei和关系-实体对(rk，ej)之间的注意力计算如式（3）所示：

其中：o∈Rd表示一个参数向量；◦表示按元素乘。由于在实体ei的一跳邻域中可能有多个关系-实体对，因此使用Softmax 计算式（3）得到的aijk进行归一化，如式（4）所示：

其中：Rin表示链接实体ei与N(ei)中包含实体的关系集合。随后，对实体ei邻域中的关系-实体对的嵌入向量进行加权，计算聚合之后的信息，如式（5）所示：

与式（1）的形式类似，通过对实体ei的嵌入向量ei与s进行整合，以构建实体ei的最终嵌入表示，如式（6）所示：

注意力的计算过程与聚合信息的过程如图1所示，图中使用实体与关系-实体对之间的注意力聚合实体ei一跳邻域中的实体ej和关系rk的信息，其中，αijk表示注意力，φ表示向量的组合运算。同时，编码器可能需要聚合实体ei邻域中的多跳信息。因此，使用投影操作对关系的嵌入向量进行线性变换，如式（7）所示：

其中：Wr∈Rd×d1为线性变换投影矩阵。投影之后的关系嵌入向量维度与式（6）中的hi相同。当需要聚合实体邻域中的多跳信息时，只需重复执行式（3）～式（7）。

2.2 解码器

受CNN 在知识图谱补全上应用［11-12］的启发［24-25］，本文使用CNN 对实体-实体类型元组(e，t)进行建模，构建知识图谱实体类型补全模型CE2T 作为解码器。该解码器由卷积层、池化层、投影层和内积层组成。CE2T 的评分函数定义为：

其中：e∈Rd1表示编码器输出的实体最终嵌入向量（式（6）中的hi），d1 表示编码器输出的最终实体嵌入向量的维度；t∈Rℓ表示实体类型的嵌入向量，ℓ表示实体类型嵌入向量的维度；Ω表示卷积核的集合；W表示投影矩阵；*表示卷积运算；pool(·)表示池化操作；vec(·)表示拼接成向量。

CE2T 模型的架构如图2 所示。从图2 可以看出：在前向传播过程中，e作为卷积层的输入。假设卷积核Ω∈R|Ω|×1×f，步长为cs，其中|Ω|为卷积核的个数，1×f为卷积核的大小。则卷积层的输出F=σ(e*Ω)∈R|Ω|×a×b，其中a=1，b=(d1-f)/cs+1。卷积层的输出F作为池化层的输入。设池化的窗口大小为1×p，步长为ps。则池化层的输出P=pool(F)∈R|Ω|×m×n，其中m=1，n=(b-p)/ps+1。之后，将P重新拼接成向量vec(P)∈R|Ω|·m·n作为投影层的输入。

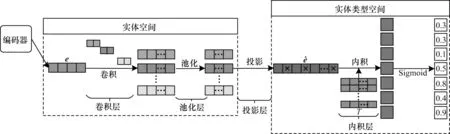
图2 CE2T 模型架构Fig.2 Framework of the CE2T model

由于实体和实体类型是知识图谱中不同层次的对象［6］，因此在解码器CE2T中存在两个不同的向量空间，分别记为实体空间和实体类型空间。投影层的作用是将卷积层和池化层提取的实体嵌入向量特征投影到实体类型空间。CE2T 模型与ConnectE［11］模型都采用了类似的投影策略，但ConnectE 模型投影的是实体的嵌入向量e，而CE2T 模型投影的是实体的特征向量（共|Ω|个，具体数量等于卷积核的个数）。投影层的权重W∈R|Ω|·m·n×ℓ。在实体类型空间中的实体投影向量=σ(vec(P)·W)∈Rℓ。最后，实体的投影向量通过内积与实体类型的嵌入向量t计算得到相似性评分。式（1）中的Ω和W是共享参数，独立于e和t。

2.3 NACE2T 模型的训练

为了快速训练NACE2T 模型，本文使用文献［12］提出的1-N评分，即对一个实体的投影向量和所有实体类型的嵌入向量t进行评分，如图2 中的内积层，其中T表示所有实体类型的嵌入向量组成的矩阵。同时，使用Sigmoid 函数将ϕ(e，t)归一化到0～1 之间，即p=Sigmoid(ϕ(e，t))，并通过最小化二元交叉熵损失函数训练NACE2T 模型的参数。NACE2T 的损失函数定义如下：

其中：y∈R|T|表示二进制的标签向量；T表示所有实体类型的集合；|T|表示实体类型的个数。如果(e，t)为真，则y的相应位置为1，否则为0。优化器选择Adam。

2.4 问题定义与实现

知识图谱实体类型补全的目标是推断给定实体e的类型t。对于在测试集中的每个实体e，NACE2T推断的实体类型为：

NACE2T 模型推断实体所属类型的过程如下：首先，对于任意实体e，通过式（8）计算后得到|T|个评分，例如数据集FB15KET 含有3 854 个实体类型，则对于FB15K 中的任意实体，根据式（8）计算后得到3 854 个评分；然后，通过式（10）对这|T|个评分进行排序，排序之后的最大值对应的实体类型为NACE2T 模型推断的实体类型。此外，对于NACE2T 模型，实体和实体类型之间的相似性评分是一个相对的指标。NACE2T 模型使得正确实体类型和实体之间的相似性评分尽可能高，而错误实体类型和实体之间的相似性评分尽可能低。

3 实验

本文实验代码使用Python 实现，首先，使用CE2T 与NACE2T 进行知识图谱实体类型补全实验，其次，对NACE2T 模型中向量的组合方式、关系-实体对的个数和卷积核的个数进行分析。

3.1 数据集

在知识图谱补全中经常使用的两个数据集是FB15K［15］和YAGO43K［10］，分别是Freebase 和YAGO的子集。实体类型补全使用的实体-实体类型元组数据集（形式为实体、实体类型）称为FB15KET［10］和YAGO43KET［10］，分别将实体类型映射到FB15K 和YAGO43K 中的实体。FB15K 和FB15KET 与YAGO43K 和YAGO43KET 的统计数据如表1 所示。编码器使用三元组数据集FB15K 和YAGO43K 来利用关系信息。CE2T 使用实体-实体类型元组数据集FB15KET 和YAGO43KET 学习实体类型的嵌入表示并进行实体类型补全。

表1 数据集的统计数据Table 1 Statistics data of datasets

3.2 实验设置

3.2.1 评价标准

本文采用知识图谱补全任务中基于排名的标准对NACE2T 模型进行评估［15］。首先，对于每个测试的实体-实体类型元组(e，t)，移除类型；然后，根据式（10）进行评分并排序；最后，根据正确实体类型获得确切排名。本文采用两个指标进行评估：平均倒数等级［15］（MRR）和预测排名前k的正确实体类型比例［15］（HITS@k）。MRR 与HITS@k的计算如式（11）和式（12）所示：

其中：|NET|表示测试集中实体-实体类型元组的数量；ranki表示第i个实体-实体类型元组的正确实体类型的位置；|Nk|（k取1、3、10）表示排名前k的正确实体类型个数。MRR 和HITS@k的值越大表示模型具有更优的性能。

3.2.2 参数设置

本文使用网格搜索确定模型的最佳参数。在实体邻域中关系-实体对的个数在［1，100］之间调整，实体和关系的嵌入维度在［50，200］之间调整，实体类型的嵌入维度在［100，300］之间调整，编码器输出的嵌入向量维度在［200，600］之间调整，批训练大小batch 在｛128，256，512｝中调整，学习率在［0.000 05，0.001］之间调整，CE2T 中卷积核的个数在｛10，32，64，128｝中调整，卷积核的大小在｛1×2，1×4，1×8｝中调整，卷积步长在［2，8］之间调整。池化选择最大池化，窗口大小为1×2，步长为2。

3.3 实体类型补全结果分析

基线模型选择RESCAL-ET［10］、HOLE-ET［10］、TransE-ET［10］、ConvKB［24］、CapsE［26］、ETE［10］和ConnectE［11］。不同模型的评价指标对比如表2 所示，加粗表示最优数据。

表2 不同模型的评价指标对比Table 2 Evaluation indicators comparison among different models

从表2 可以看出，与最先进的ETE 模型和ConnectE 模型相比，本文所提的NACE2T 模型具有较优的结果。在不使用编码器的情况下，CE2T 模型也取得较优的效果，说明模型表达能力的提升可以提高实体类型补全的性能。相比RESCAL-ET、HOLE-ET、TransE-ET、ConvKB 和CapsE，NACE2T模型在实体类型补全性能上得到显著提升。

在FB15KET 数据集上，CE2T 模型在所有评价指标上相较于ETE 模型提高了约7%，与ConnectE 模型的各项指标基本持平。NACE2T 模型相比ConnectE 模型的各项指标提高约1.5%。

在YAGO43KET 数据集上，CE2T 模型相较于ETE模型和ConnectE 模型在MRR、HITS@1 和HITS@3 上分别提升约4%、6.5%和4.5%。同时，NACE2T 模型相比CE2T 模型在各项指标上提升约2%，说明实体邻域中实体和关系的信息有助于推断实体所属的实体类型。

此 外，RESCAL-ET、HOLE-ET 和TransE-ET 实体类型补全实验的效果不佳，其原因是这些模型选用的知识图谱补全方法使实体按类型聚类的效果一般。本文选择FB15KET 中4 个实体类型且这4 个实体类型分别包含不同的实体。图3 所示为使用RESCAL［16］、HOLE［17］和TransE［15］训练的实体嵌入向量经过t-SNE 降维后的散点图。

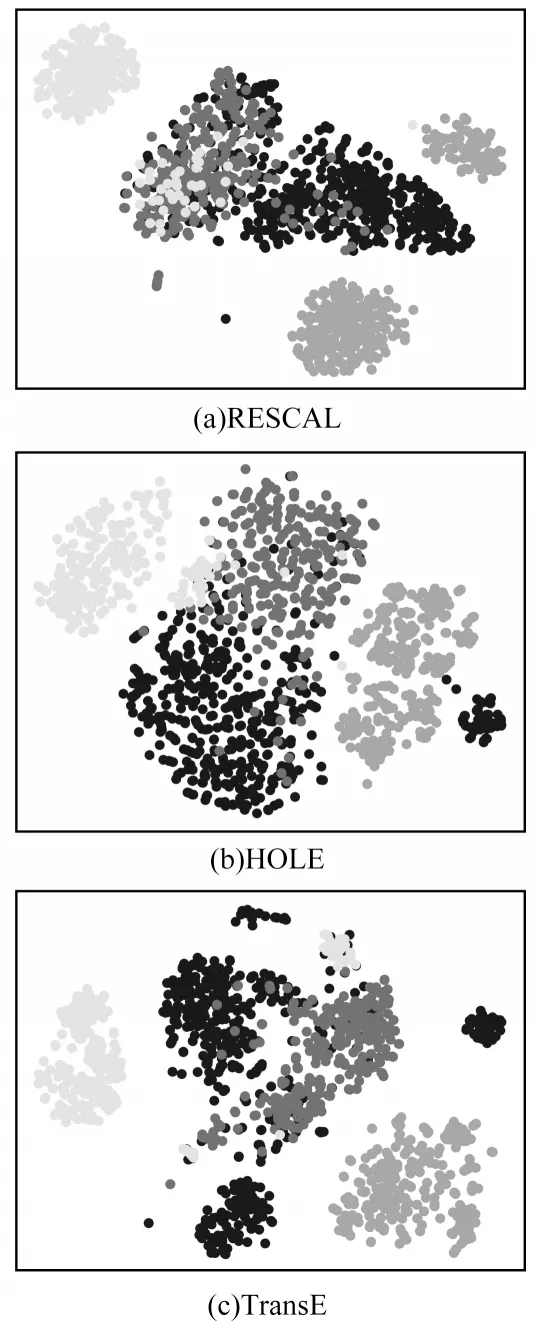
图3 RESCAL、HOLE 和TransE 训练的实体嵌入向量可视化效果Fig.3 Visualization effect of entity embedding vectors trained by RESCAL，HOLE and TransE

从图3 可以看出：4 个实体类型分别包含不同的实体，但都存在重叠的问题，说明聚类效果较差，特别是RESCAL。RESCAL-ET、HOLE-ET 和TransEET 在训练过程中不改变实体嵌入向量e，仅改变实体类型的嵌入向量t，使模型的性能极度依赖于RESCAL、HOLE 和 TransE 的聚类效果。而RESCAL、HOLE 和TransE 的聚类效果较差，间接导致RESCAL-ET、HOLE-ET 和TransE-ET 实体类型补全效果降低。ConnectE 同样选择使用TransE 对实体嵌入向量进行训练，但是ConnectE 模型的实体类型补全性能相对于TransE-ET 模型有较大的提升。其主要原因是ConnectE 模型中包含一个可学习的投影矩阵M，虽然ConnectE 与TransE-ET 的训练方式大致相同，但是可学习投影矩阵M的存在使ConnectE的学习性能优于TransE-ET。

在知识图谱中一个实体通常会有多个实体类型，记为1-N，例如实体“Jackie Chan”的类型可以是“Actor”，也可以是“Person”。NACE2T 通过编码器利用了实体邻域中的信息，特别是关系的信息，因此，能够有效地对1-N的情况进行建模。

为检验NACE2T 对1-N情况（由于本文的目标是推断实体e的类型t，因此仅存在1-1 与1-N，不存在N-1和N-N等）进行建模的效果，本文首先将FB15KET 和YAGO43KET 的测试集划分为1-1 和1-N两部分，然后在这两部分测试集上分别使用ETE、ConnectE、CE2T和NACE2T 进行实体类型补全实验，实验结果如表3和表4 所示。

表3 不同模型在1-1 实体类型补全实验上的评价指标对比Table 3 Evaluation indicators comparison among different models on 1-1 entity type completion experiment

表4 不同模型在1-N 实体类型补全实验上的评价指标对比Table 4 Evaluation indicators comparison among different models on 1-N entity type completion experiment

从表3 和表4 可以看出：NACE2T 在1-1 和1-N上的评价指标均优于ETE、ConnectE 和CE2T。其原因为NACE2T合理地利用了实体邻域中实体和关系的信息，而这些信息有助于NACE2T 捕获实体在对应不同类型时的差异，能够更有效地对1-N情况进行建模。

3.4 向量组合方式对NACE2T 性能的影响

向量的组合方式φ(·，·)主要有：1）void：φ(u，v)=u；2）sub：φ(u，v)=u-v；3）corr：φ(u，v)=u★v。其中：★表示循环相关运算［17］；void 表示聚合信息的过程中不聚合关系的信息。该实验在FB15K 与FB15KET 上进行，结果如表5 所示。

表5 NACE2T 利用不同向量组合方式的评价指标对比Table 5 Evaluation indicators comparison of NACE2T using different vector combinations

从表5 可以看出：NACE2T（corr）和NACE2T（sub）的评价指标优于NACE2T（void），说明关系嵌入向量中包含的信息有助于推断实体的所属类型。同时，当φ(u，v)=u-v时，NACE2T 模型具有较优的效 果。除φ(u，v)=u以 外，对于不同的φ(u，v)，NACE2T 模型在实体类型补全上的表现相差不明显。

3.5 关系-实体对个数对NACE2T 性能的影响

在实体邻域中关系-实体对的个数在［1，100］中调整，本文实验在FB15KET 和YAGO43KET 数据集上进行。关系-实体对个数对NACE2T 模型评价指标的影响如图4 所示。NACE2T 模型在FB15KET 数据集上的MRR 对应于图4 的左侧坐标，在YAGO43KET数据集上的MRR 对应于图4 的右侧坐标。

图4 关系-实体对个数对NACE2T 模型评价指标的影响Fig.4 Influence of number of relationship-entity pairs on evaluation indexes of NACE2T model

从图4 可以看出：当关系-实体对的个数为1 时，NACE2T 在一定程度上会退化为CE2T 模型，此时NACE2T 的性能与CE2T 相似。随着关系-实体对个数的增加，NACE2T 的性能不断提高。在FB15KET数据集上，当关系-实体对个数为20 时，NACE2T 具有较优的评价指标。当关系-实体对个数大于60 时，NACE2T 的性能呈明显的下降趋势，这是因为在进行实体类型补全时，实体邻域中的某些关系-实体对的信息会成为噪声，使NACE2T 不能充分地捕获实体在对应不同类型时的差异，导致性能降低。同时，侧面反映出不是所有关系-实体对都对推断一个实体的所属类型有帮助。对于YAGO43KET 数据集，同样存在这种下降的趋势。

3.6 卷积核个数对NACE2T 性能的影响

为验证卷积核个数对NACE2T 模型性能的影响，本文在实验中仅改变卷积核的个数，其他参数保持不变。卷积核的个数在［1，80］中调整。在不失一般性的情况下，在FB15KET 数据集上卷积核个数对NACE2T 模型评价指标的影响如图5 所示。

图5 卷积核个数对NACE2T 模型评价指标的影响Fig.5 Influence of the number of convolution kernels on evaluation indexes of NACE2T model

从图5 可以看出：NACE2T 的性能随着卷积核个数的增加而增加。当卷积核的个数大于40 时，模型性能趋于平稳。当卷积核的个数为64 时，模型具有较优的性能。因此，NACE2T 模型的性能不会随着卷积核的改变出现较大的波动。

4 结束语

本文提出基于邻域聚合与CNN 的知识图谱实体类型补全模型。基于注意力机制设计用于利用关系信息的编码器，通过对实体与其邻域中的关系-实体对计算注意力，并将其用于聚合实体邻域中实体和关系的信息。同时，针对现有知识图谱实体类型补全模型表达能力不足，本文基于CNN 设计知识图谱实体类型补全模型CE2T 作为解码器，对编码器输出的实体最终嵌入向量和实体类型的嵌入向量进行建模。实验结果表明，与RESCAL、HOLE、TransE 等模型相比，本文所提的NACE2T 模型在MRR、HITS@1、HITS@3、HITS@10 评价指标上得到显著提升。后续将解纠缠表示学习应用于NACE2T 模型，并进行实体类型补全，以提高模型的表达能力和模型实体类型补全的准确率。