简支下承式钢管混凝土系杆拱桥稳定性参数研究
曹少华
(中铁四局集团第五工程有限公司,江西 九江 332000)
1 工程概况
圭河大桥为简支下承式钢管混凝土系杆拱桥计算跨径为122 m,矢高为24.4 m,矢跨比为1/5,其中拱肋的拱轴线选择二次抛物线型,拱肋在竖直方向投影面上的线形方程为:Y=4×24.4×(122-X)X/1 222(m)。拱肋为向内倾8°的提篮拱式结构,造型优美,拱肋拱顶处的两拱中心距为6.542 m。拱肋截面选择哑铃型状钢管混凝土等截面布置,截面高度为3.2 m,每根拱肋的两钢管之间用腹板连接,拱肋之间的横向连接采用一字横撑和K字横撑组合布置。吊杆沿拱肋的倾斜面上均匀布置,同样其横向倾角为8°。主梁全长为124.8 m,选用单箱三室预应力混凝土带悬臂的箱型截面,主梁桥面板宽为17.6 m,底板宽为15.0 m。
2 结构有限元模型与参数的选取
2.1 结构有限元模型
结合桥梁工程设计图纸建立简支下承式系杆拱桥模三维有限元模型,拱肋、拱肋间横向连接、系杆、桥面系纵横梁均采用空间梁单元进行模拟,而吊杆采用桁架单元模拟,边界条件、材料特性参数以及作用荷载与实际工程中一致。
2.2 结构参数的选取
结合简支下承式钢管混凝土系杆拱桥的受力特征,根据第一类稳定问题对结构的空间稳定性分析,依托工程案例,选择实际设计或施工过程中对桥梁结构稳定性有着较大的影响的设计参数,结合实际工程案例中的经验来选取参数的合理范围设计过程中的经验,以此来得到不同结构参数变化范围。采用单一控制变量法分析,在其他条件不变的前提下,挑选拱肋倾角、拱肋横撑、拱肋刚度、矢跨比以及吊杆布置形式等结构设计参数对简支下承式钢管混凝土系杆拱桥进行空间稳定性系数进行计算,分析简支下承式钢管混凝土系杆拱桥在最不利荷载工况下的屈曲稳定性系数。
3 下承式钢管混凝土拱桥稳定性参数分析
3.1 拱肋倾角
简支下承式钢管拱桥大部分采用平行拱肋的设计方式,提高了施工的便捷性,但不利于结构的空间稳定性。而拱肋与竖直方向呈一定倾角时,能够在一定程度上提高结构的空间稳定性,因此通过改变拱肋与竖直方向的倾角,分析结构整体稳定性随拱肋与竖直方向的倾角变化的趋势,结合有限元软件分别建立六种不同拱肋倾角的三维空间模型,采用特征值法计算其屈曲稳定系数,分析简支下承式钢管拱桥的整体稳定性随拱肋与竖直方向的倾角变化的趋势。计算结果如图1所示。
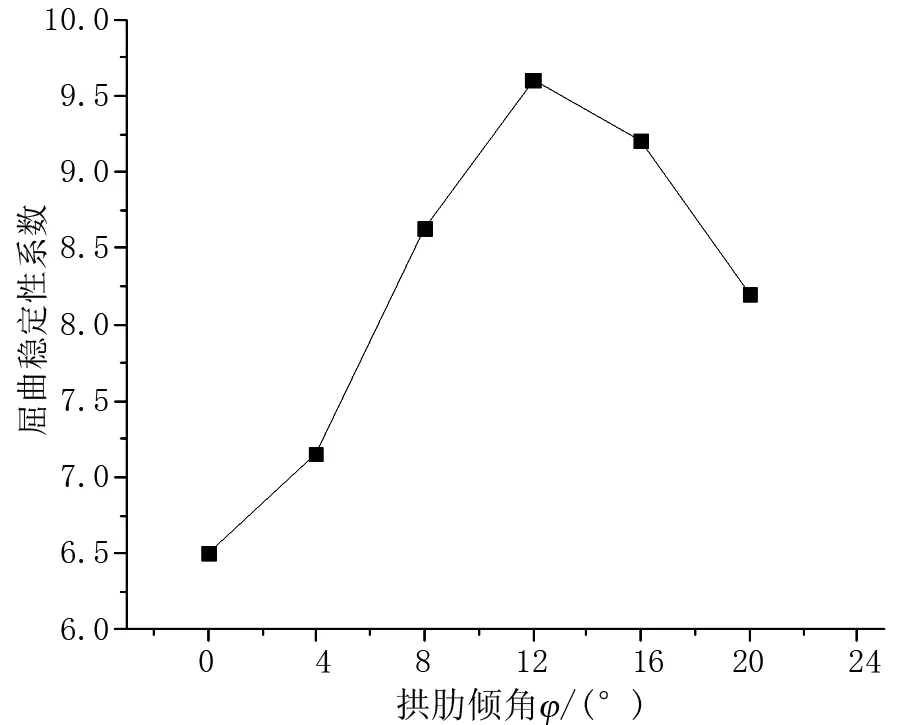
图1 屈曲稳定系数随拱肋倾角的变化规律
如图1所示,对比不同拱肋与竖直线的内倾角度下的结构空间稳定性系数相对变化规律,当拱肋与竖直线的内倾角度逐渐增大,简支下承式拱桥的屈曲稳定系数逐渐增大,当拱肋与竖直线的内倾角度增加达到12°时,结构的空间稳定性能达到峰值,拱肋内倾角超过12°以后,拱桥结构的空间稳定性逐渐降低。因此拱桥拱肋与竖直线呈现一定的夹角时,能够在一定程度上提高结构整体稳定性能,能够有效解决施工过程中出现的面外失稳问题,同时也能提高桥梁的美观性。但当拱肋与竖直线的内倾角度达到临界值时,由于两拱肋之间的距离太小,导致拱肋组合横向刚度比较小,致使拱桥结构整体稳定性降低,同时拱肋倾角过于大会提高结构施工难度,因此122 m简支下承式钢管混凝土系杆拱桥的最佳拱肋内倾角为12°,其稳定性能较拱肋平行布置时提高了47.7%。
3.2 拱肋横撑
简支下承式钢管混凝土拱桥通常采取在两拱肋之间设置横撑的方式来提高拱肋间的横向稳定性,因此在其他设计参数保持不变的条件下,计算时仅改横撑布置形式,分别对比分析无横撑、“一”字形横撑,“K”字形以及“X”字形四种形式的拱肋横撑下的结构整体屈曲稳定性系数,计算结果如图2所示。
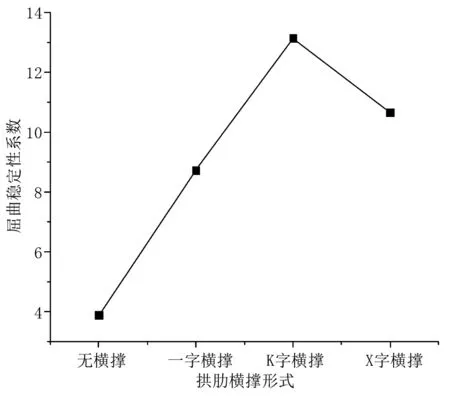
图2 屈曲稳定系数随拱肋横撑布置形式的变化规律
如图2所示,当两拱肋之间没有横撑时,此时结构的屈曲稳定性系数仅为3.89,不满足规范所要求的大于4,因此两拱肋之间不能不布置横撑。一字横撑和X字横撑能够显著增大屈曲稳定系数,而选择“K”字横撑布置时,此时结构的稳定性能最强的,其屈曲稳定系数为13.16,相较于无横撑布置时,稳定系数提高了240%,这是因为K字横撑与拱肋之间形成了类似三角形的稳定结构,两拱肋与横撑之间的整体刚度大大提升,极大地增加了结构的空间稳定性,因此大部分简支下承式钢管混凝土系杆拱桥选择K字横撑作为平联。
3.3 拱肋刚度
为了分析拱肋刚度对结构整体稳定性的影响规律,在其他情况不变的前提下,分别取拱肋抗弯刚度为0.4EI、0.8EI、1.2EI、1.6EI以及2.0EI五种情况考虑,建立不同的有限元模型,研究结构整体稳定性系数随拱肋刚度的变化规律,计算结果见图3所示。
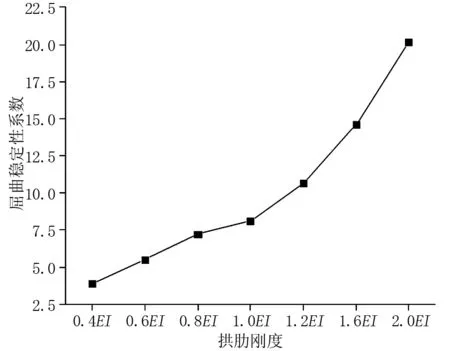
图3 屈曲稳定系数随拱肋刚度的变化规律
由图3分析可知,随着拱肋结构的抗弯刚度的加强,简支下承式拱桥的屈曲稳定性系数逐渐变大,其空间稳定性能明显得到改善,并且随着抗弯刚度越大,屈曲稳定性系数的提高也越明显,因此当简支下承式拱桥整体稳定性能不足要求时,能够通过适当加强拱肋的刚度,以此提升拱桥结构的空间稳定性能。
3.4 矢跨比
简支下承式拱桥矢跨比的合理选择对拱桥系梁与拱肋的受力状态有所影响,并且也影响着结构施工方法以及美观性,更重要的是对结构整体稳定性的影响很大。通过控制其他设计参数保持不变,变化矢高来调整矢跨比分析整体稳定性,取矢跨比分别为1/2.5、1/3.0、1/3.5、1/4.0、1/4.5、1/5.0、1/5.5以及1/6.0,分析拱桥结构屈曲稳定系数随不同矢跨比的变化规律,计算结果如图4所示。
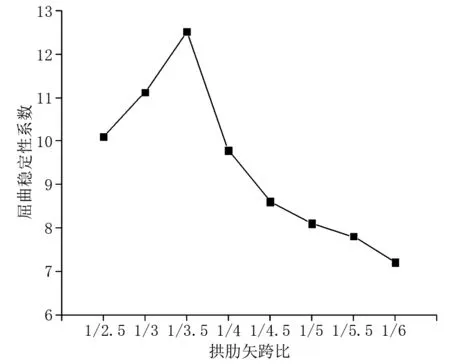
图4 屈曲稳定系数随拱肋矢跨比的变化规律
根据图4所示,随着矢跨比从1/2.5逐渐下降到1/6,结构的空间稳定性能并没有立即下降,而是呈现小幅度的增强后再逐渐减小的变化趋势,其中在矢跨比为1/3.5的时候结构空间稳定性能最强,其屈曲稳定性系数为12.5。然而在工程实践中,一味的选择较大的矢跨比会使得拱桥结构的经济性降低,同时也会提高施工技术难度,增加施工风险,相反,如果拱桥结构的矢跨比小,即使能够减小施工成本,降低施工难度,但会导致桥梁的整体稳定性降低,并且结构的美观性也会受到影响。
3.5 吊杆布置形式
简支下承式系杆拱桥结构中的系杆与拱肋是通过吊杆来传递力的,对结构的受力状态影响很大。因此不同吊杆的布置形式也会对结构的整体稳定性影响不同,在工程实践中,经常使用竖直吊杆、倾斜吊杆以及网格吊杆。其他条件不变的前提下,计算时仅改吊杆布置形式,分别对比分析竖直吊杆、倾斜吊杆以及网格吊杆三种形式吊杆的结构整体屈曲稳定性系数,计算结果如表1所示。
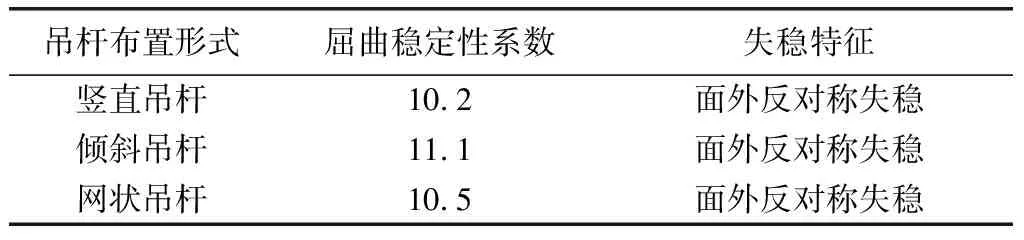
表1 不同吊杆布置形式下的结构整体稳定性系数与失稳特征
由表1可知,三种吊杆布置形式下结构的整体稳定性均满足要求,其中采取网状形式布置吊杆的结构屈曲稳定性系数最大,最小的为竖直形式布置吊杆,但两者相差仅8.8%,因此在结构设计过程中,除有必要对拱桥结构进行美观性设计外,在结构整体稳定性满足规范要求的前提下,建议大部分选择竖直形式布置吊杆。
4 结 论
(1)调整拱桥拱肋倾角时,能够在一定程度上提高结构整体稳定性能,能够有效解决施工过程中出现的面外失稳问题,同时也能提高桥梁的美观性。
(2)拱肋布置横撑能够提升结构的空间稳定性能,其中拱肋间布置K字横撑结构相较于不布置横撑结构的稳定性系数提升了240%,因此合理布置拱肋间横撑对简支下承式钢管混凝土拱桥的空间稳定性提升很大。
(3)随着拱肋结构的抗弯刚度的加强,简支下承式拱桥的屈曲稳定性系数逐渐变大,其空间稳定性能明显得到改善,并且随着抗弯刚度越大,屈曲稳定性系数的提高也越明显,故可通过适当加强拱肋的刚度,以此提升拱桥结构的空间稳定性能。
(4)随着矢跨比的减小,结构的空间稳定性能呈现小幅度的增强后再逐渐减小的变化趋势,因此在实际工程中合理选择矢跨比有利于拱桥结构空间稳定性能的提升。
(5)三种吊杆布置形式下结构的整体稳定性能差别不大,因此在结构设计过程中,除有必要对拱桥结构进行美观性设计外,在结构整体稳定性满足规范要求的前提下,建议大部分选择竖直形式布置吊杆。

