基于深度学习的小学数学错题讲评策略研究

徐梅梅

【摘要】深度学习是一种批判性的学习模式，注重对教学内容的深度感知、深度理解、迁移应用与批判创新.以深度学习模式为基础开展小学数学错题讲评教学工作，对于加深学生错误认识，提升学生识错、纠错、改错等能力有着重要意义.文章深入剖析了深度学习的概念，结合小学数学错题讲评教学案例提出几点教学建议，指出教师可以通过呈现错题、分析错因、组织改错、组织再练等方式确保学生在错题讲评中实现深度学习，以期为提升小学数学错题讲评教学质量提供参考.

【关键词】深度学习；小学数学；错题讲评；策略

错题是一种宝贵的教学资源.基于错题开展教学讲评工作，有利于学生认清自身的学习不足，引导学生基于自身问题进行反思、提高，从而锻炼学生的综合能力.然而，现阶段的小学数学错题讲评仍然存在讲评模式单一、讲评程度不深刻等问题，造成学生的浅层学习问题.为此，小学数学教师有必要优化错题讲评方式，通过创新策略、创新方法、创新过程驱动学生深度学习，确保错题的教学价值被充分发挥.

一、认识：呈现错题使学生直观感知错误

学生认识错误是开展错题讲评工作的前提，也是学生开始深度学习的基础.然而，部分小学生由于自身的知识储备不够扎实，思维发展程度不高，不能在做题时发现自身的错误.因此，在实际教学中，教师应发挥自身的教学指导作用，在教学中注意观察、发现学生的习题错误，并应用直观的教学手段将学生的错误直接呈现在学生面前.通过直观呈现的方式让学生认识到自身的错误，从而增强学生对错题讲评学习的认识，为之后教师的教学工作顺利开展奠定基础.

例如，在人教版二年级数学下册“有余数的除法”一课的错题讲评时，教师可以预先批改学生的习题，再以PPT的形式将学生的错题呈现出来，如：

16÷3=4……4 23÷5=3……8

38÷6=6……4 47÷7=6……7

先给学生2～3分钟时间，让学生观察错题，初步激发学生的纠错意识.在此过程中，教师还可以鼓励学生以同桌为单位或以小组为单位讨论观察结果，如：我认为16÷3=4……4的错误和23÷5=3……8的错误是相同的错误，都是余数大于等于除数；我认为38÷6=6……4的错误是运算错误，余数应该是2；等等.在这一步骤，有的学生并不能发现错题的全部错误，仅能挑出部分错误.这时，教师可以应用PPT呈现正确答案，进一步增强学生对错题的直观感受：

16÷3=5……1 23÷5=4……3

38÷6=6……2 47÷7=6……5

通过先呈现错题组织观察与讨论，激活学生的改错思维，再呈现错题正解，组织学生对比与分析，进一步加深学生对错误的认识.这样，学生能够对习题错误有更加深刻的感知，为以后的深度学习奠定了坚实的基础.

二、分析：开展综合活动使学生理解错误原因

爱因斯坦曾经说过：“学习知识要善于思考，思考，再思考.”基于深度学习的小学数学错题讲评教学要确保学生的学习主体地位.只有保证学生学习思维的活跃性，才能够确保学生在思考中取得收获，在收获中丰富认知.对此，教师应在错题讲评教学中组织多样化的教学活动，借助综合活动激活学生的识错思维，使学生明晰自身错误原因，为接下来的纠错、改错教学做好铺垫.

1.评前测评，增强学生错题感悟

“对症下药”才能有奇效.如果教师不明确学生的学习情况，只从“教”的角度出发开展讲评工作，难免会出现讲评内容不符合学生学习需求，讲评过程不满足学生发展需求等问题.要避免上述问题发生，就需要教师全面掌握学生的学习情况.为此，教师有必要在错题讲评教学前开展前测活动，在前测活动中出示与错题有关的测评习题，让学生在完成测评习题的过程中认识到自身的学习不足，对错题形成初步感悟.同时，通过讲前测评，教师可以更加全面地掌握学生的学习情况，进一步增强错题讲评教学的针对性.比如，在“多位数乘一位数”的错题讲评之前，教师可设计如下测评习题：

（3）估算39×5≈（ ），因为39接近（40），所以（40）×（5）=（200）.

以上测评题目围绕多位数乘一位数的算理、算法以及估算等基本教学知识点展开，重点测评学生对基础内容的掌握情况.完成测评后，教师可以分析学生的测评结果，并针对学生的测评情况对学生学情进行分析，如：能够正确回答所有测评问题的学生，说明学生扎实掌握算理、算法，且具有良好的估算、分析、运算能力；正确回答填空题，但估算题回答错误，说明学生的理论能力较好，但运算能力不足；不能正确回答理论问题，同时估算题目错误，说明学生理论能力、运算能力都不足.这时，教师可以制订针对性的讲评方案，如：针对各方面能力不足的学生，可以将运算算理、算法作为错题讲解重点，先让學生明理悟法，再引导其感知错题改正方法；针对运算能力不足的学生，教师可以先出示简单问题，让学生准确回答简单问题后类比迁移错题，引导学生自主改题.这样，教师通过设计不同的错题讲评方案，满足不同类型学生的错题学习需求，进一步增强了学生的错题学习感悟.

2.对比错题，加深学生错误理解

在小学数学教学过程中，由于学生的数学学习基础、数学理解能力、学习习惯存在差异，其在解题过程中犯的错误也并不相同.如果教师采取“一刀切”的方式开展错题教学，很容易限制学生的思维发展，造成学生的浅层学习问题.因此，在错题讲评教学中，教师可以提前分析不同学生的错题情况，对学生的错题进行归类，再利用PPT将各类错题呈现给学生，并组织学生对比分析，让学生指出不同错题的错误类型，最后由教师针对错题进行深度讲评，进一步加深学生对错误的理解.比如，在“多位数乘一位数”一课的习题教学中，教师可以将学生的错题提炼出来，分析其错因，如：因算理掌握不扎实造成的错误；因算法应用错误造成的错误；因运算失误造成的错误等.之后，教师可以使用PPT将不同类型错题呈现出来：

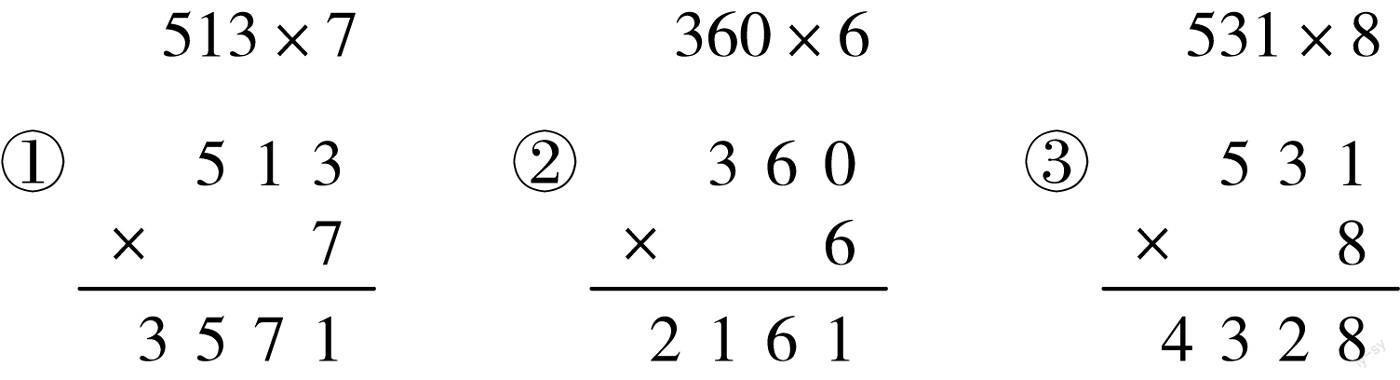
其中，第①题的错误原因主要在于学生对“进位”算法掌握程度不够，并没有在计算3×7时进位，导致计算错误；第②题错误的原因在于学生对“0乘以任何数都得0”这一算理掌握程度不够，导致计算错误；第③题的错误原因在于学生计算失误，将531×8看成了541×8计算出错误答案.通过对比呈现不同错题，让学生明确因算理不明、算法应用失误、马虎所造成错误的特点，进一步加深学生对错误原因的理解.这样，教师再开展错题讲评工作，就能够进一步提高学生的识错、纠错、改错学习效率.

三、联想：关联旧知使学生应用知识改错

根据布鲁姆教学目标分类理论，可以将认知领域教学目标分为知识、领会、运用、分析、综合、评价六个层次.其中，知识、领会为浅层学习的目标层次；运用、分析、综合、评价为深度学习的目标层次.在完成错题的呈现讲评、分析讲评后，教师可组织学生基于错题回顾所学内容，引导学生在回顾旧知的过程中探究错题改正的方法，从而锻炼学生的分析思维、综合思维等多种思维能力.

例如，在人教版四年级下册“运算定律”一课的错题讲评时，针对错题134-75+25=134-（75+25）=134-100=34，教师可以先组织学生观察习题，判断此习题中应用到的运算定律，如：此习题考查了加法结合律与减法的运算性质.其中，加法结合律即一个数加上一个数再加上一个数，可以先算后两个加数的和，再用后两个加数的和与第一个加数相加，用字母表示为a+b+c=a+（b+c）；减法的运算性质即一个数减去一个数，再加上同一个数，某数不变，用字母表示为（a-b）+b=a；一个数减去一个数，再加上另外一个数，可以先用减数减去加数，再用被减数减去计算结果，用字母表示为a-b+c=a-（b-c）.学生回顾完理论知识后，教师再引领学生对照数学公式对比、分析错题内容，让学生纠出题目错误，如：134-75+25这一习题的形式与加法结合律a+b+c=a+（b+c）与a-b+c=a-（b-c）计算模型具有相似之处.但是，加法结合律中的三个数以加号作为连接，而错题的三个数分别用加号、减号连接，说明这道题主要考查的是减法的运算性质，可以套用a-b+c=a-（b-c）这一计算模型进行解答，如134-75+25=134-（75-25）=134-50=84.但错题在应用加法结合律时未在括号内变符号，导致计算错误.这样，学生在联想旧知的过程中轻松判断题目正误，明确错题的错误原因（即运算律应用时忘记改变符号），同时应用正确的运算方法改正错题，从而完成错题认识、错误分析、错题纠正、错误总结等学习任务，学生的综合思维得到充分锻炼.

四、再练：错题再练使学生形成创新思维

避免学生再犯类似的错误是错题讲评教学的主要目的.深度学习视域下，教师应进一步调整教学目标，将培养学生建构、迁移、应用、创新思维作为错题讲评教学的最终目标.为此，教师不光要对错题展开讲解，还要依据错题展开迁移教学、创新教学，借助相应的教学活动引领学生将讲评教学的内容迁移到错题解答、变式题目解答过程中，从而发展学生的创新思维，促使其达到深度学习的状态.下面，文章结合人教版六年级上册“分数除法”一课的错题讲评教学案例，分析如何通过错题再练驱动学生形成创新思维.

1.错题再练，巩固学生讲评学习所得

将学生的错题作为练习教学资源，组织错题再练教学活动，有助于巩固学生讲评教学所学基础，进一步提高学生的解题能力.在完成错题的错因讲评、改错讲评等讲评教学工作之后，教师可以利用课堂剩余时间组织错题再练教学活动.在活动中，教师将学生的错题原题板书在黑板上，随机叫两名学生上讲台解答错题，剩余学生在自己座位上解答错题.然后，教师组织其他学生评价上台答题学生的题目是否解答正确，再对再练后的解题情况给予讲评，通过讲后再练、练后精讲的方式，进一步巩固学生的学习所得.

2.錯题再变，发展学生习题迁移思维

基于原有错题设计新问题，并围绕新问题组织学生审题、解题，可以检测学生的错题讲评学习成果，同时发展学生的迁移应用思维与创新思维.在实际教学中，教师可以在完成基本讲评任务后组织“错题再变”练习活动，依据学生的错题设计变式问题，并组织学生在规定的时间内解决变式问题，让学生在解决变式问题的过程中联想错题讲评教学内容，自觉规避解题错误.

以原错题为基础设计类型相似的变式问题.通过出示变式问题激活学生的迁移思维、应用思维与创新思维，使学生自觉联想错题讲评的教学内容列出分数除法算式，并正确应用分数除法的算理、算法解答错题变式问题.这样，不仅能充分巩固学生的错题讲评学习基础，还可以提高学生创新应用的数学解题能力，真正达到深度学习的状态.

结 语

综上所述，合理利用错题开展认识、分析、联想、练习教学，对于巩固学生数学知识基础，培养学生质疑反思思维，锻炼学生纠错、改错能力有着重要意义.小学数学教师应认识到错题讲评教学的重要性，同时综合深度学习的相关育人理念、育人理论开展错题讲评工作，从而在讲评教学中使学生认识自身错误，改正自身错误，进一步促进其综合提升.但是，要实现这一教学构想，还需要教师不断学习教学理论，积累教学经验，尝试创新教学方法，才能够不断推进小学数学错题讲评教学的持续发展.

【参考文献】

[1]邓兰婷.例谈小学数学错题的有效利用[J].读写算，2022（32）：135-137.

[2]周沁珏.小学生数学错题资源高效应用意识的培养[J].小学生（上旬刊），2022（9）：124-126.

[3]赵婧.小学数学错题的利用现状及改进措施[J].小学生（下旬刊），2022（8）：121-123.

[4]高兴社.小学数学错题分析活动中思维导图的应用研究[J].试题与研究，2022（12）：42-43.