并行耦合动态整数帐篷Hash函数设计

刘玉杰 刘建东 刘 博,2 钟 鸣 李 博

1(北京石油化工学院信息工程学院 北京 102617) 2(北京化工大学信息科学与技术学院 北京 100029)

0 引 言

Hash函数最早由Knuth在1950年提出，它是一种单向函数，用于将大数据块压缩为该数据的较小的固定大小表示形式，称为消息摘要或Hash值[1-2]。作为现代密码学的重要研究内容之一，Hash函数在信息安全领域中起着至关重要的作用，同时也是近几年正兴起的区块链技术中的关键技术之一，密码学家王小云因其所带领的课题组成功碰撞了MD5等经典加密算法获得2019年未来科学大奖“数学与计算机科学奖”，Hash函数的研究再一次获得了社会各界的关注。

安全是哈希函数的首要要求[3]，在MD5等传统Hash算法被王小云教授课题组成功碰撞后，业界迫切需要寻找更加安全的Hash函数构造方法。传统的Hash函数构造大多使用按位AND、OR、XOR和MOD等运算符来对数据进行杂凑处理，以增强其哈希输出中的随机性。文献[4]提出了一种具有多项式函数的构造方法，提升了部分性能，但是同样避免不了使用上述运算符。2002年出现了一种利用混沌模型构造Hash函数的方法，其利用较少的运算符就能充分使数据随机性增强，成为一种新的研究思路，并且出现了较多的基于混沌映射的Hash算法。混沌系统具有良好的特征，与加密要求有很强的关联性[5-6]。典型的混沌系统模型主要有连续系统模型和离散系统模型，帐篷映射就是一种经典的离散混沌系统。将基于混沌的Hash函数构造方法与传统Hash函数构造方法相结合，即将帐篷映射整数化，既能凸显出基于混沌的Hash函数的优良特性，又能避免出现因精度效应导致的安全缺陷。同时通过添加动态参数，成立动态整数帐篷映射，这样既可以避免整数帐篷映射的短周期行为，又保有其伸长与折叠的非线性本质。最后利用耦合映象格子对动态整数帐篷映射进行耦合，极大地提高了系统的混乱与扩散性质，进而使其在应用中具有更高的安全性[7]。

除安全性问题外，效率是Hash函数的另一个重要问题。Rivest在Crypto2008上提出了MD6算法，MD6算法的数据块大小为512字节，(而MD5的数据块大小是512比特)，链值长度为1 024比特，可从其中摘出0～512比特的值作为最终Hash值，最重要的是MD6算法在其中增加了并行机制，非常适用于多核CPU，契合了时代的发展。另外SHA系列也是利用MD迭代结构，其效率随着文件大小的增加而迅速下降，所以目前研究方向是提出一种新颖的Hash函数，这种Hash函数在处理大量数据时可以保持较高的效率[8]。随着信息时代的发展，产生巨大信息的同时，也要能够快速地对大量数据进行处理，多核处理器技术(CMP)的发展提供了快速运算的可能。基于上述原因，本文采用MD6算法框架，利用多核处理器技术，设计出一种核心算法采用耦合动态整数帐篷映象格子模型的新型并行Hash函数算法。

1 耦合动态整数帐篷映象格子模型

1.1 动态整数帐篷映射

将帐篷映射进行整数化，并引入动态参量，即得到动态整数帐篷映射。它不仅解决了整数帐篷映射的短周期问题，还具备帐篷映射均匀分布的特性，性能优良[7]。其数学描述如下：

(1)

gi=(xi+ki)mod 2n

(2)

F映射中(图1)，ki为动态变量，表示“帐篷”横坐标移动的距离，控制其水平移动。xi表示第i步迭代结果；2n为x(i)取值的整数集上界。迭代运算中，随着i值的变化，ki取不同的值，即ki的值与算法迭代步数有关，既保证了动态性又保证了的算法的稳定性，不会使得因动态参数改变而使最终值改变。

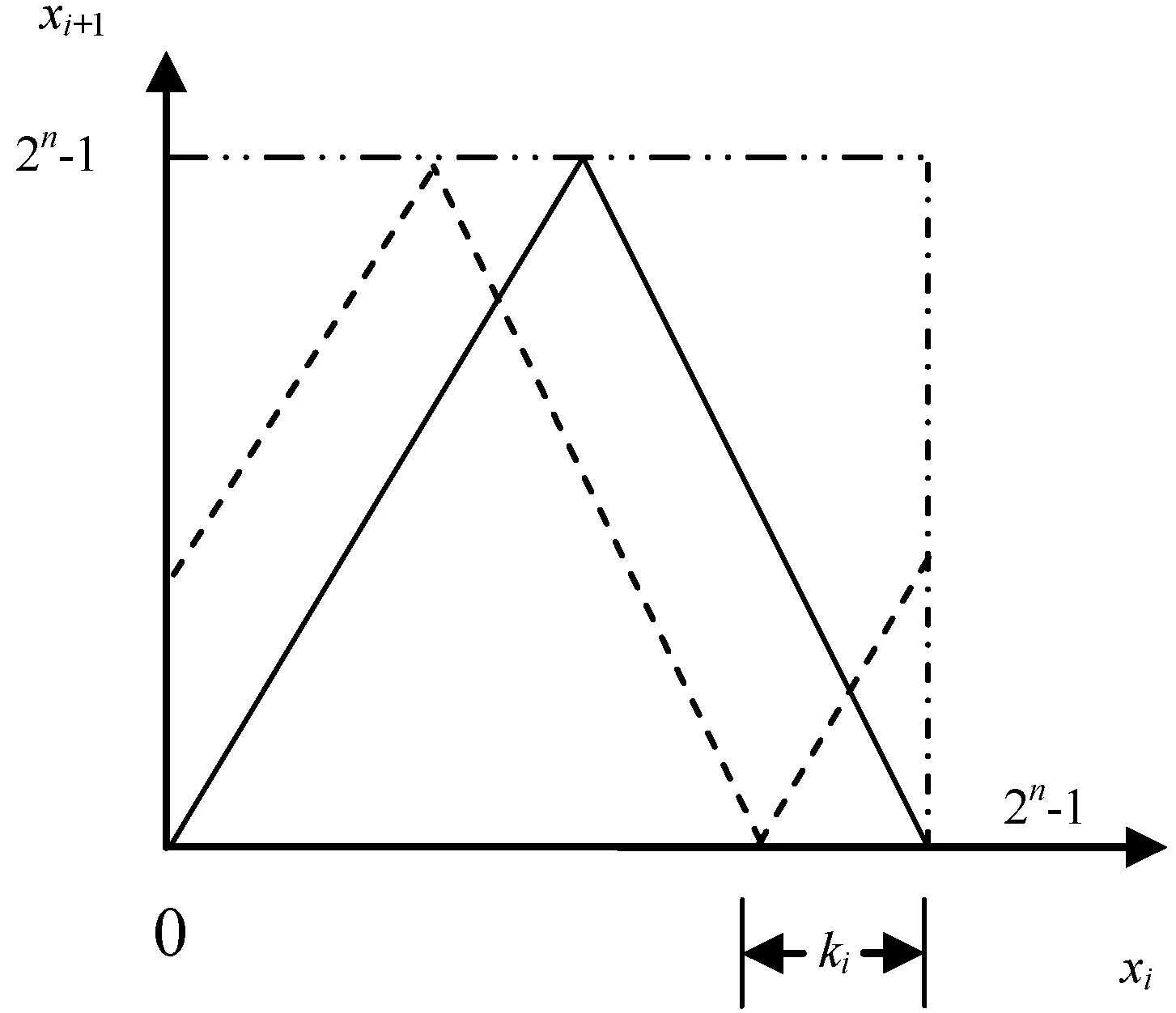
图1 动态整数帐篷映射

1.2 耦合动态整数帐篷映象格子模型

利用耦合映像格子模型(CML)将动态整数帐篷映射进行耦合，进而获得性能更好的密码序列。CML所生成序列的复杂性直接影响其构造出的密码系统的安全性，而其又受到所选用的非线性函数、系统格子规模大小、耦合系数及非线性函数参数的取值等的影响[9]，将耦合映象格子系统的非线性函数选为动态整数帐篷映射，耦合方式如下：

xi(n+1)=

(f[xi(n)]+f[xi-1(n)]+f[xi+1(n)])mod 2k

(3)

式中：xi(n+1)表示第i个格点的第n+1步迭代所得状态值；f(·)表示格点的非线性函数)；2k为格点取值的状态数目。每一个格点既由上一步迭代的三个格点值所影响，又能对下一步迭代的三个格点产生影响，其过程如图2所示。图2中，实心点表示格点，空心点表示虚拟格点，虚拟格点为迭代计算提供边界条件[9]。

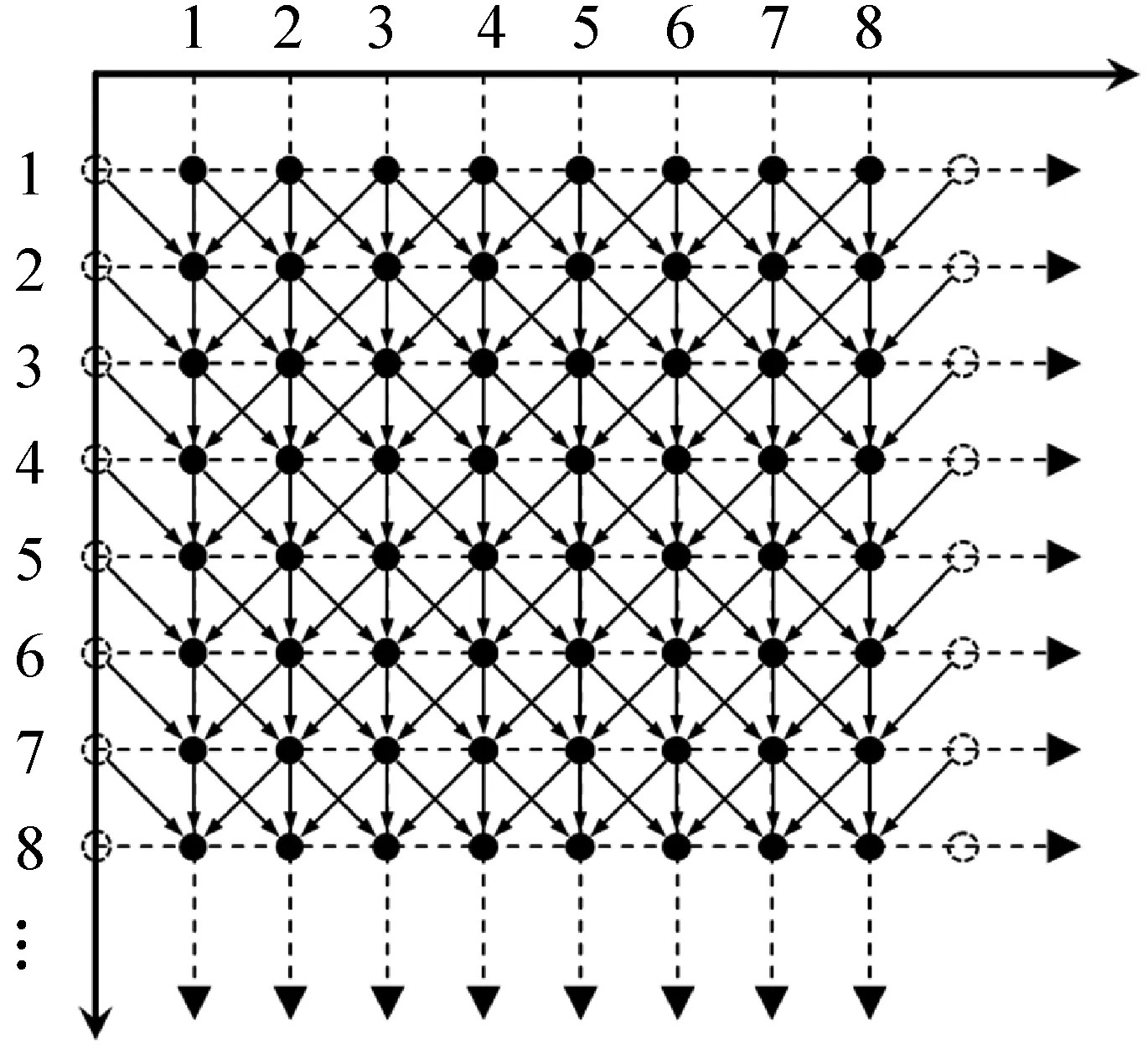
图2 模型耦合方式

2 多核并行计算技术

多核处理技术(CMP)是在一块芯片上集成两个及以上的处理器核，通过这种方式来增强芯片计算性能。CMP通过在两个及以上的CPU核上分配工作负荷，并且依靠内存和输入输出的高速片上互联和高带宽管道对系统性能进行提升。较之当前的单核处理器，多核处理器能带来更多的性能和生产力能效。因此针对多核处理器设计对应的加密算法能够使得杂凑算法更加快捷。

同时利用英特尔的超线程技术，把多线程处理器内部的两个逻辑内核模拟成两个物理芯片，举例来说就是单个处理器就能够模拟出两个线程来实现并行，进而兼容多线程操作系统和软件。超线程技术充分利用空闲CPU资源，在相同时间内完成更多的工作。通过超线程技术，可以将双核心的处理器，模拟出4个线程处理器的效果。本文所有测试都是在Intel(R) Core(TM) i5- 6200U@2.30 GHz 2.40 GHz双核处理器，利用超线程技术模拟出四个线程实现。

各种并行计算平台的存在允许各种算法和操作的并行实现。一种流行的并行平台是共享内存并行机(SMPM)，它是一种多核共享内存计算机，通常使用OpenMP(开放式多处理)API[10-11]。OpenMP采用Fork-Join模型，如图3所示。

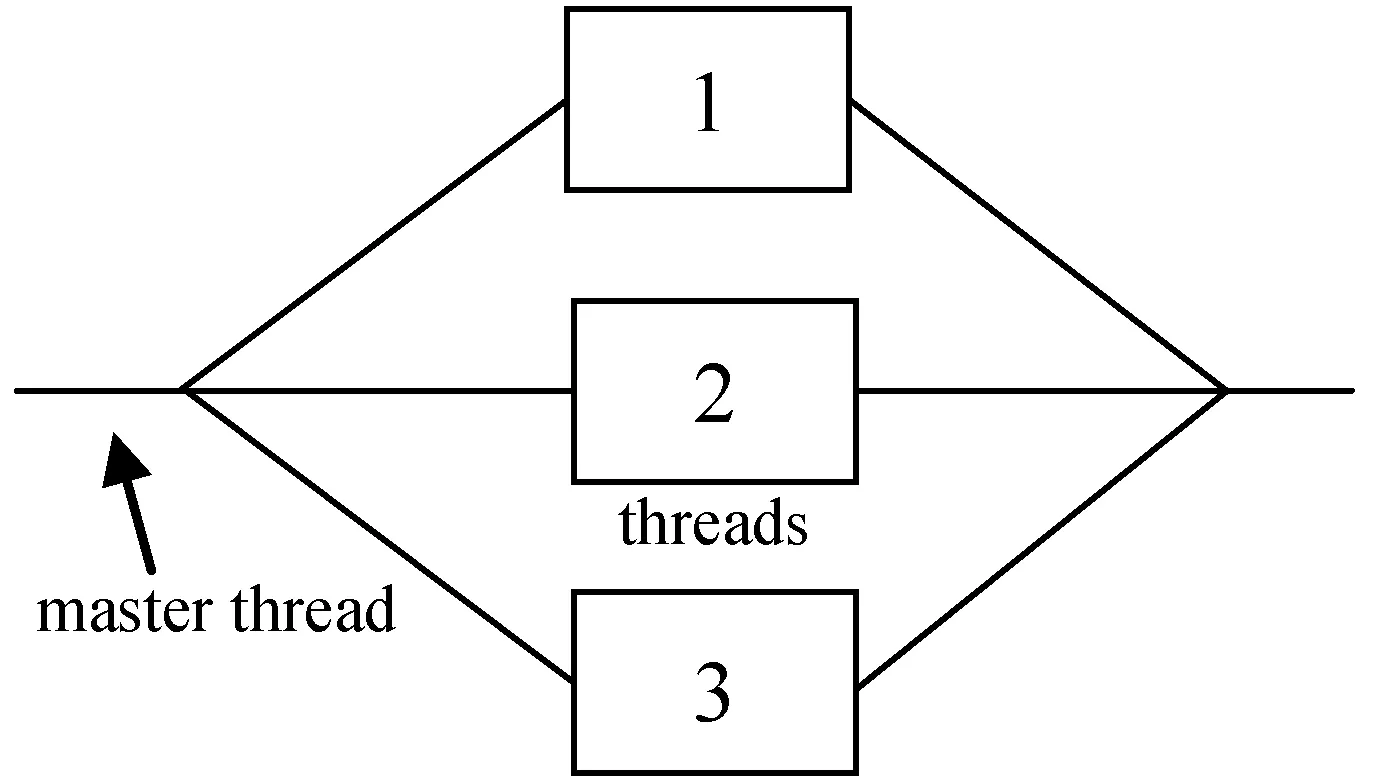
图3 Fork-Join模型

OpenMP由Compiler Directives(编译指导语句)、Run-time Library Functions(库函数)等组成，使用方式比较容易，很多研究人员做并行算法都会首先选择使用。本文算法也是使用了openMP中的sections-section实现了并行。

3 并行Hash函数构造

3.1 运算模式

执行模式的确定。参数L确定如图4的Merkle树的执行模式。MD6中L默认值为64，此时为一颗完整的Merkle树，执行模式为并行模式；如果L值等于0，则为串行模式，按顺序串行执行；如果L的值介于0和64之间，则进行混合模式，首先从层次0到层次L，然后在每个层次内按顺序压缩函数。本文中取L=64，以实现并行化。

数据填充。算法的输入参量为长度小于264比特的消息，算法中的计量单位是“字”，一个“字”等于8字节，图4中每个节点的大小为16个“字”，所以进行一次压缩函数运行需要64个“字”的初始输入。要实现4个线程并行处理数据，进行运算的数据应满足其形成的节点数为4的次幂，即总字节数除以128后为4的次幂。所以算法先对初始数据进行判断，如果不能满足上述情况，则用“0”进行填充，以满足条件。

算法运算模式如图4所示。可以看出，整棵树被分成四个部分，每一个部分由一个线程执行，最后将四个线程的结果汇总到一起进行最后一次Hash计算并从中得到摘要值。利用openMP的fork-join模式，先划分再汇总，以实现并行化提升效率。每个线程中的运行方式相同，收到足够的消息块即512字节的数据即调用压缩函数，逐级深入，整个过程只需要开辟一个很小的结构体空间，存储各级数和当前需处理的数据等信息[13]。

图4 Merkle树

3.2 压缩函数

压缩函数的输入是大小为80个“字”的数据块，其具体表示如图5所示。Q为一个15个“字”的向量，这一部分可以修改。U为节点ID号，其大小为1个“字”，指示分块的位置，包括节点所在层次和在层次内具体位置，大小分别为1个字节和7个字节。B是大小为64个“字”的数据块，与4个16的“字”的节点相对应。

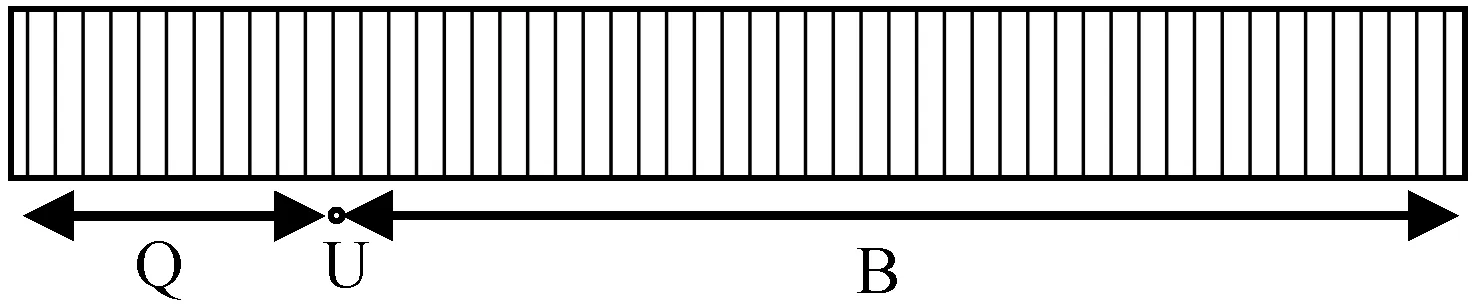
图5 压缩函数的输入

取系统格子规模L=16，对应最终节点大小16个“字”。压缩函数核心步骤如下[14]：

1) 将每个压缩函数的输入划分成20×32字节的消息字m0，…，mp，…，m19。

2) 每个消息字按从高到低位划分为4×8个字节：C1、C2、C3、C4。

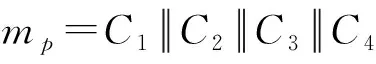
3) 嵌入消息块Mn。具体嵌入过程如下所示。总共需要进行两轮操作，每一轮操作执行4次迭代过程。两轮操作过后，每个消息字都被使用了4次，在每一轮中将消息块与格点变量进行混合。

第一轮：

第8×n次迭代：

xj,8×n=xj,8×n+mpj=0,…,4;p=0,…,4

第8×n+1次迭代：

xj,8×n=xj,8×n+1+mpj=0,…,4;p=5,…,9

第8×n+2次迭代：

xj,8×n=xj,8×n+2+mpj=0,…,4;p=10,…,14

第8×n+3次迭代：

xj,8×n=xj,8×n+3+mpj=0,…,4;p=15,…,19

第二轮：

第8×n+4次迭代：

第8×n+5次迭代：

第8×n+6次迭代：

第8×n+7次迭代：

4) 在对所有的消息块进行如上操作之后,接着对式(4)进行r次迭代，取出最后一次迭代结果，即得到最后的16个“字”的输出，然后在从中截取长度为d的最终Hash值。

4 实验结果与分析

4.1 数据敏感性分析

首先分别对以下几种情况的消息文本进行仿真实验：

T1:2.5Mbytes大小的消息文本。
T2：第一个大写字母变为小写。
T3：中间一个句号变为逗号。
T4：删除末尾的一个字符。
T5：将中间的‘a’变为‘b’。

通过实验得到的各种情况十六进制Hash值分别为：

T1:9c4b00e85d2d12a6e45d4cc43beccfa2。
T2：5d6d72613c163a7697b6eb8ec05579ee。
T3：a63b3d85950c8d42a87a931ac36eaef2。
T4：b050eadf93061e6a799470e9abaccd0e。
T5：f4841a6b5b442b169d8f81d42bb71e2e。

如果采用0，1序列来表示Hash值，上述各种情况对应的结果如图6所示。从仿真结果可以看出，明文消息文本的微小改变一定会对Hash值的生成产生极大的影响。

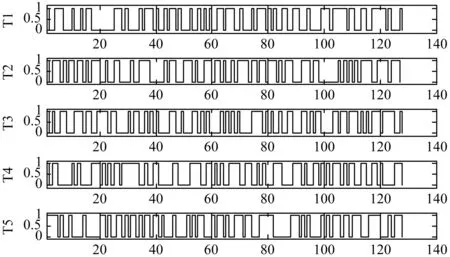
图6 Hash值对明文消息敏感度的测试

4.2 混乱与扩散性质统计分析

一般用以下4个统计量来检测算法的混乱与扩散性质：

(1) 平均比特变化数：

(4)

(2) 平均比特变化率：

(5)

(3) 比特变化数的均方差：

(6)

(4) 比特变化率的均方差：

(7)

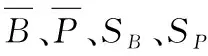
表1 混乱与扩散性质统计结果

4.3 抗碰撞性分析

Hash函数的抗碰撞性是检验其安全性的一个重要测试，如果能够找到两个不同的明文消息，其经过算法处理后产生的Hash值相同，则称为碰撞攻击。方法如下：首先选取一段明文消息求出其Hash值，以ASCII字符来表示；然后改变明文中1 bit的值，得经过计算得到一个新的Hash值。对两个Hash值进行比对，若两个Hash值在相同位置上的ASCⅡ字符相同，则称被击中1次。测试结果如图7所示，1 024次测试中有83次测试击中1次，2次测试击中2次，5次及以上是16次，碰撞率约为0.098 633。

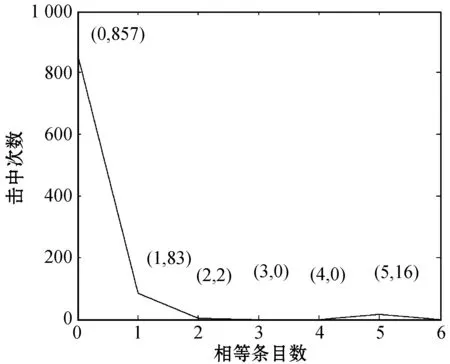
图7 相同位置上ASCII字符相同的数目分布

4.4 字符距离测试

字符距离是一种用来检验两个不同明文消息产生的Hash值是否相互独立的统计量，定义如下：

(8)

式中：d为字符距离；H1[i]和H2[i]分别为用十进制数来表示的两个不同Hash值的第i个字节的值；s为所得的Hash值的字节长度。如果两个被检验的Hash值独立并且各字节取值服从均匀分布，所求得的平均字符距离值理论上应为85.33。测试方法同抗碰撞检验类似，在求得一段明文消息的Hash值后，随机改变1比特明文，求得一个新的Hash值，比较两个Hash值的字符距离。共进行1 024次测试，得平均字符距离为85.89，同时通过表2与其他算法进行对比，本算法的平均字符距离非常接近理论值，可以认为更改原明文消息1 bit后，新的Hash值与原Hash值是相互独立的。

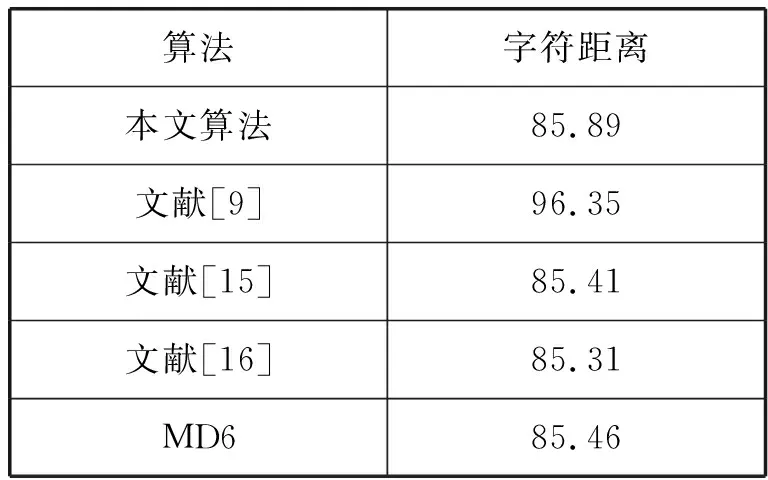
表2 算法的平均字符距离

4.5 NIST随机性测试

NIST测试套件是由15个测试组成的统计软件包，这些是为了测试随机(任意长度)由基于硬件或软件的密码随机或伪随机数生成器产生的二进制序列。测试关注于各种不同类型的已存在的非随机序列。有些测试可以分成各种子测试。NIST测试主要检测P_value的值与设定值α的大小比来判断是否通过测试，α取值为0.01。若P_value≥α，则通过该项测试。测试结果如表3所示。本文提出的Hash函数算法生成的序列通过了其中13项测试，可以认为生成的序列是一个比较理想的随机序列。

表3 NIST随机性测试结果

4.6 执行效率测试

当初始消息块的长度不能满足被分成四块后每块形成的数据块个数为4的次幂时，需要进行数据填充，经检测此部分占用了大量时间去处理，这也是下一步需要改进的地方。图8显示的是初始数据满足条件时各线程运行时间的对比。可以看出在开启1、2/3、4线程算法运行时间是递减的；在开启2/3线程运行时间相近是因为都为将4块数据分为两步处理，因此执行速度差别较小。

图8 算法运行时间

5 结 语

本文采用MD6架构，利用merkle树来实现并行化，压缩函数核心为耦合动态整数帐篷映射，结合传统逻辑函数，使得帐篷映射整数化，并加入动态参量，最后使用耦合映象格子模型，充分发挥了混沌系统的随机性。同时利用merkle树的结构，并行化处理数据，使得杂凑速度在开启多核情况时倍速增长。对比文献[9]可以用在对数据量较大的信息进行杂凑处理。虽然由于数据填充部分使得在填充数据时可能会占用大量时间，但是算法通过了各项测试，可以说是有价值的，值得在未来信息安全中使用。