基于Kinect的手方向实时估计系统

姚 玲 陈建新 潘招来 黄湘君

(南京邮电大学通信与信息工程学院 江苏 南京 210000)

0 引 言

人机交互已有30多年的历史，其发展极大地丰富了用户体验[1]。在人机交互领域，对人体骨骼姿态的追踪已经变得越来越重要，这主要是由于它们在医疗、生物医学、人机界面、虚拟现实、机器人技术等领域的应用[2]。手作为人体骨骼中最灵活的关节，被认为是最方便、最有效的交流工具，因此对手姿势的估计一直是一个热门领域。文献[3]提出了一种将17个惯性传感器(IMU)和中央处理器(CPU)集成在可穿戴式感应手套上来捕捉手关节的自由度。文献[4]提出了一种在大拇指、中指和手背上分别带三个IMU传感器来估计手和手指之间的相对方向。这种基于传感器的方法虽然准确度较高但是手上需要佩戴设备，视野和跟踪范围受到一定的限制。文献[5]提出一种利用更快的卷积神经网络(CNN)的主干生成矩形区域检测手并提取特征，旋转网络生成一个与手对齐的估计面来估计手方向。文献[6]提出了一种利用卷积神经网络(CNN)来检测手的边界框，并将与手边界框对齐的向量的方向作为手的方向。基于卷积神经网络的方法需要大量的数据集来训练，准确度高，但是实时性差，并且在环境改变时会对准确度有影响。文献[7]提出了一种利用几何方法来计算角度并结合分解四元数算法(FQA)[8]对手方向进行估计。文献[9]提出了一种将手的手掌区域和手指区域分离，并提取出手掌中心点和手的中指点、拇指点来估计手方向。几何方法是计算关节角度的一种常用方法，简单易行，但是在准确获取关节位置信息的基础上，抖动和噪声较大，准确度不高。因此，上述方法对手方向进行估计时的缺陷可归结为实时性差以及准确率低。针对此问题，本文提出一种基于Kinect的手方向实时估计系统。该系统可以准确、实时对手方向进行估计，并利用开放图形库(OpenGL)构建一个3D的虚拟手模型，模仿手的实时运动，提高了人机交互的体验。

1 系统设计

本文系统框图如图1所示，首先通过深度数据寻找目标用户，结合从Kinect获得骨骼数据找到目标用户的手腕点的位置，并利用Holt双指数平滑滤波算法对手腕位置的骨骼点坐标进行平滑处理；然后将从Kinect获得手腕点的四元数转换为欧拉角以便可以直观地观察手的方向变化。为了消除由Kinect噪声引起的欧拉角抖动，利用一种将卡尔曼滤波和中值滤波结合的算法来平滑欧拉角，滤除噪声。最后，对计算出的欧拉角进行可视化，主要通过两种方法，分别是在彩色图像中绘制代表手方向的坐标系以及运用OpenGL构建3D手模型。

图1 手方向实时估计系统框图

1.1 寻找目标用户

深度传感器(Kinect)以其成本低，提供彩色图像数据以及来自红外传感器的深度数据的特点而在人机交互领域越来越被研究者青睐[10]。与传统的彩色摄像头不同的是，Kinect深度传感器能够克服彩色摄像头易受光线等外界干扰的缺点，准确跟踪到视野范围内的人体[11]。Kinect可以同时跟踪六个用户，并为这六个用户分配不同的ID信息。为了防止用户间的相互干扰，导致从Kinect获取的数据不准确，本文选取距离Kinect最近的用户ID作为标记用户ID。然后，将当前帧的用户ID与标记用户ID进行匹配。用户ID完成匹配之后，检查当前帧的用户ID的跟踪状态，因为只有当前帧的用户ID的状态处于被跟踪时，Kinect才能对其信息进行处理。其算法流程如下：

1) 识别用户，利用Kinect的深度数据找到距离Kinect最近的用户ID，作为标记用户ID。

2) 搜索当前帧的用户ID，将其与标记用户ID进行匹配。

3) 如果ID值相同，则匹配成功，将当前帧的用户作为目标用户。

4) 检测目标用户的跟踪状态，如果处于被跟踪状态，就可以对Kinect输入帧的信息进行处理。

5) 如果ID匹配不成功或者目标用户状态不是被跟踪时，返回步骤1)重做处理。

1.2 骨骼点平滑

开启骨骼数据流后，当目标用户出现在Kinect的有效视野范围内，Kinect就可以迅速检测出人体并获取其骨骼信息[12]。由于从Kinect获取的骨骼信息存在噪声和抖动，因此可以通过对不同帧的骨骼信息滤波来减小抖动。滤波不可避免地会存在一定的延迟。为了确保实时性，本文使用Holt双指数平滑滤波算法[13]，因为其延迟比其他滤波算法要小。Holt双指数平滑滤波算法主要是通过5个参数进行滤波处理，这5个参数分别为：

平滑参数：代表着处理骨骼数据时的平滑量，其值在0～1之间，值越大代表平滑得越多，0代表不平滑，平滑参数增大得越多，返回的骨骼数据的延迟就越大。

修正参数：代表对原始数据的修正量，其值在0～1之间，较小的值对原始数据修正的速度较慢但会更平滑。

预测超前期数：其值应该大于等于0.5，增大该值能减小滤波的延迟。

抖动半径参数：代表修正的半径，如果抖动超过了设置的这个半径，将会被纠正到这个半径之内。

最大偏离半径参数：用来和抖动半径参数一起来设置抖动半径的最大边界。

同时，为了减少骨骼点坐标的噪声，本文对五帧连续帧的数据进行加权平均来更新当前帧的骨骼点坐标。

1.3 四元数转换

常用的两种表示姿态的方法是四元数[14-16]和欧拉角。由于四元数比欧拉角更复杂并且不够直观，因此本文选用欧拉角来表示手的姿态。欧拉角是用来描述物体旋转姿态的三个角度[17]。如图2所示，ψ、θ和φ分别定义为绕Z轴、Y轴和X轴的旋转角度。

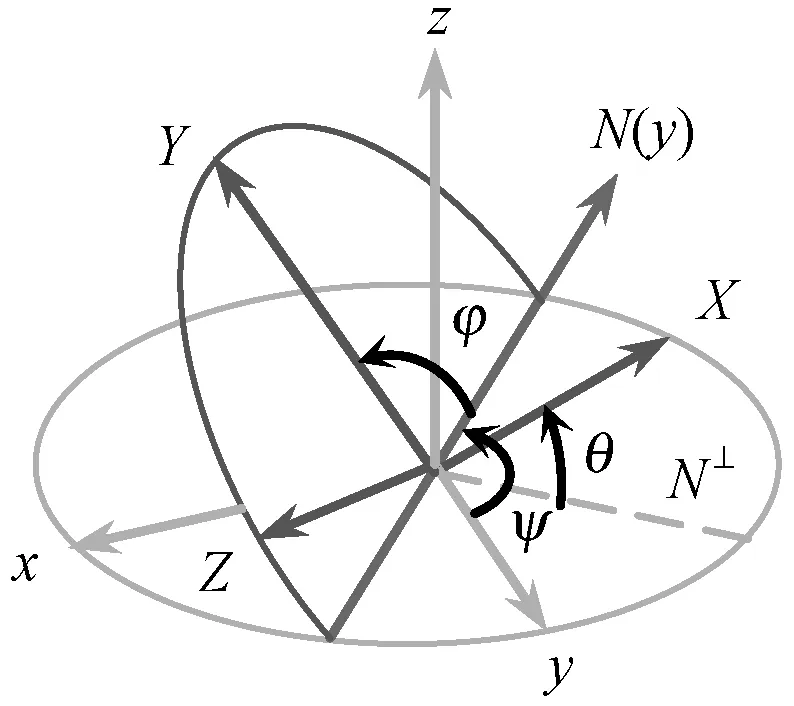
图2 欧拉角示意图

如果用卡尔丹角(Tait-Bryan angles)表示，定义欧拉角的转动顺序为Z-Y-X，则ψ、θ和φ分别对应偏航角(Yaw)、俯仰角(Pitch)、翻滚角(Roll)。

本文首先从Kinect获得手腕点的四元数q=[w,x,y,z]。然后根据式(1)将四元数转换为欧拉角。

(1)

用式(1)计算欧拉角会存在奇异解问题，发生自由度的损失。例如，当俯仰角为90度时，偏航和翻滚角就变成一个自由度[18]。为了解决这个问题，本文通过设置合理的阈值来检测俯仰角的状态。由于当俯仰角等于±90度时，wy-xz的值等于±0.5，因此，设置阈值使其尽可能接近0.5。其算法流程如下：

1) 设置阈值为0.499。

2) 计算四元数q中的wy-xz的值，如果其值在-0.499到0.499之间，则不存在奇异解问题，用式(1)计算欧拉角。

3)如果其值不在-0.499到0.499之间，则存在奇异解问题，用式(2)计算欧拉角。

(2)

1.4 欧拉角滤波

由于Kinect传感器自身存在的噪声，使得计算得到的欧拉角存在很大的噪声并且非常不稳定。对姿态进行滤波常用的算法是卡尔曼滤波[19]。卡尔曼滤波是一种基于状态空间的递归滤波算法。其模型包括状态空间模型和观测模型。前者使用状态方程来描述相邻状态矩阵的转换定律，后者则反映了实际观测值与状态变量之间的关系。滤波是将观测信息和状态转移定律结合起来，以获得对系统状态的最优估计。假设动态系统的状态空间模型是：

xk=Akxk-1+Bkuk+wk

(3)

zk=Hkxk+vk

(4)

式中：k是时间索引；xk是状态向量；zk是测量向量；Ak是状态转移矩阵；uk是控制向量；Bk是控制矩阵；wk是系统误差(噪声)；Hk是测量矩阵；vk是测量误差(噪声)。wk和vk均为高斯噪声，均服从高斯分布，即：

wk～N(0,Qk)

(5)

vk～N(0,Rk)

(6)

式中：Qk、Rk分别是wk和vk的协方差矩阵。

根据式(3)和式(4)，计算过程主要分为预测和修正两个阶段。在预测阶段，滤波器使用上一状态的估计对当前状态进行预测。主要计算过程如下:

(7)

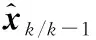
(8)

式中：yk是测量误差；Kk是最佳卡尔曼增益；xk/k为修正后的状态值；Pk/k为修正后的均方误差。

传统的卡尔曼滤波算法仅适用于线性高斯系统，且当描述系统动态特性的数学模型和噪声估计模型不准确时，无法获得良好的效果[20]。并且，卡尔曼滤波是一个递归过程[21]，所以随着滤波次数增加，舍入误差将逐渐累积。针对这个问题，本文提出一种将卡尔曼滤波和中值滤波结合的算法，首先利用卡尔曼滤波器消除在每一帧中欧拉角的噪声。然后，对连续帧的卡尔曼滤波输出进行中值滤波，将中值滤波之后输出的欧拉角作为代表手旋转方向的角。

2 实验设计

2.1 实验环境

本文实验环境为一台配置为Intel Xeon E5 2.4 GHz处理器，48 GB内存,Windows 10 64位操作系统的计算机，一个用于捕获手部动作的深度相机Kinect v2。

2.2 实验结果与分析

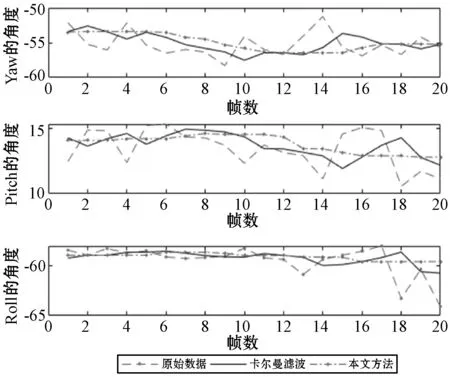
为了验证本文方法与卡尔曼滤波相比平滑效果更好，设计实验一如下：将手沿骨骼方向任意旋转，并从中选取手水平、手垂直和手倾斜时的这三个代表状态，绘制了在这三个状态时不同方法下的欧拉角变化曲线。

实验一的结果如图3所示，本文方法和卡尔曼滤波都对原始欧拉角有平滑效果，但是本文方法的平滑效果更好，使得欧拉角的波动幅度减小，变化曲线趋于更平缓，减小欧拉角的抖动的效果更明显。

(a) 手水平时的欧拉角滤波效果

(b) 手垂直时的欧拉角滤波效果

(c) 手倾斜时的欧拉角滤波效果图3 手不同状态时欧拉角的滤波效果

当手掌平面垂直于Kinect平面时，偏航角Yaw可以表示手沿骨骼旋转的角度。实验数据测量到，当手掌平面垂直于Kinect平面且正对时，偏航角等于0。当手逆时针旋转时，该角度为正；当手顺时针旋转时，该角度为负。

为了验证本文方法与卡尔曼滤波相比对欧拉角的滤波效果更好，从而使欧拉角更加稳定，设计实验二如下：将手旋转到任意11个偏航角值，然后，计算手旋转到这11个角度下不同方法滤波后欧拉角的方差。实验二的结果如表1-表3所示，表中分别列出了Roll、Pitch、Yaw角的原始方差、经过卡尔曼滤波后的方差以及经过本文方法滤波后的方差。从实验结果可以看出，经过本文方法滤波后欧拉角的方差这11个角度下都要小于经过卡尔曼滤波后欧拉角的方差。

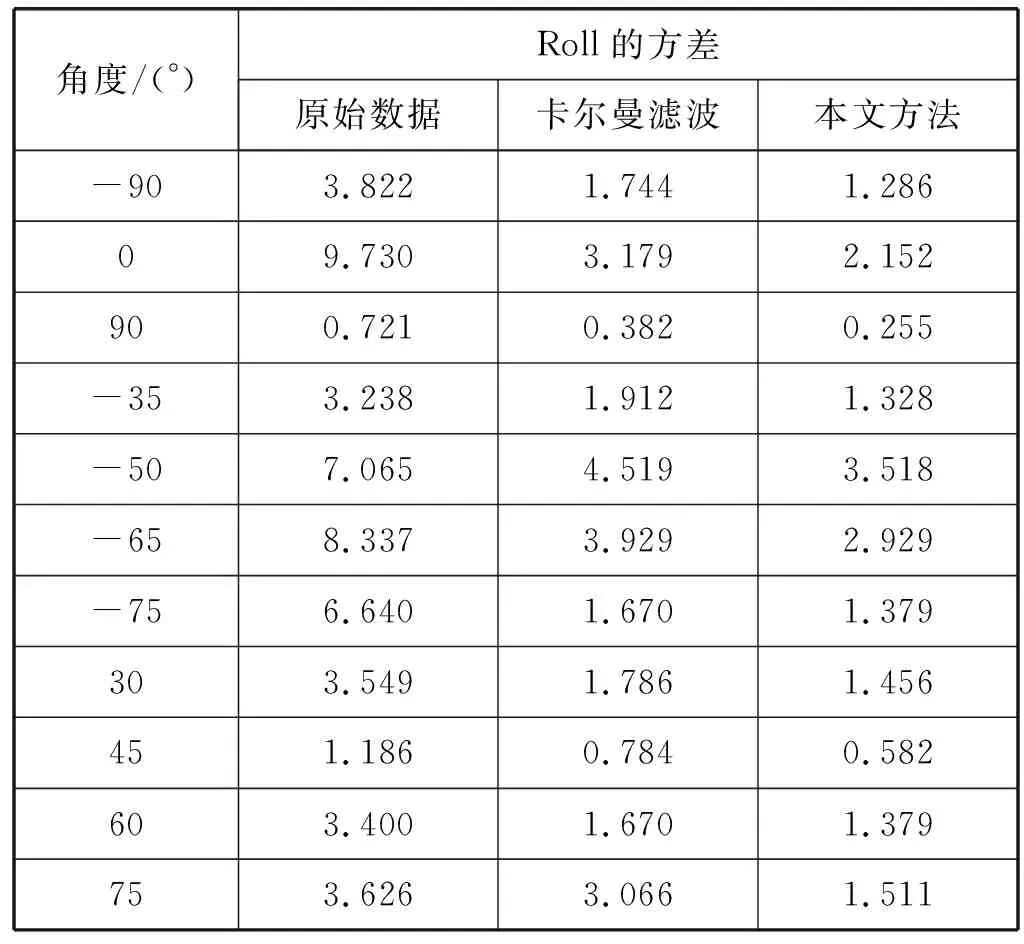
表1 不同方法滤波后Roll角的方差比较

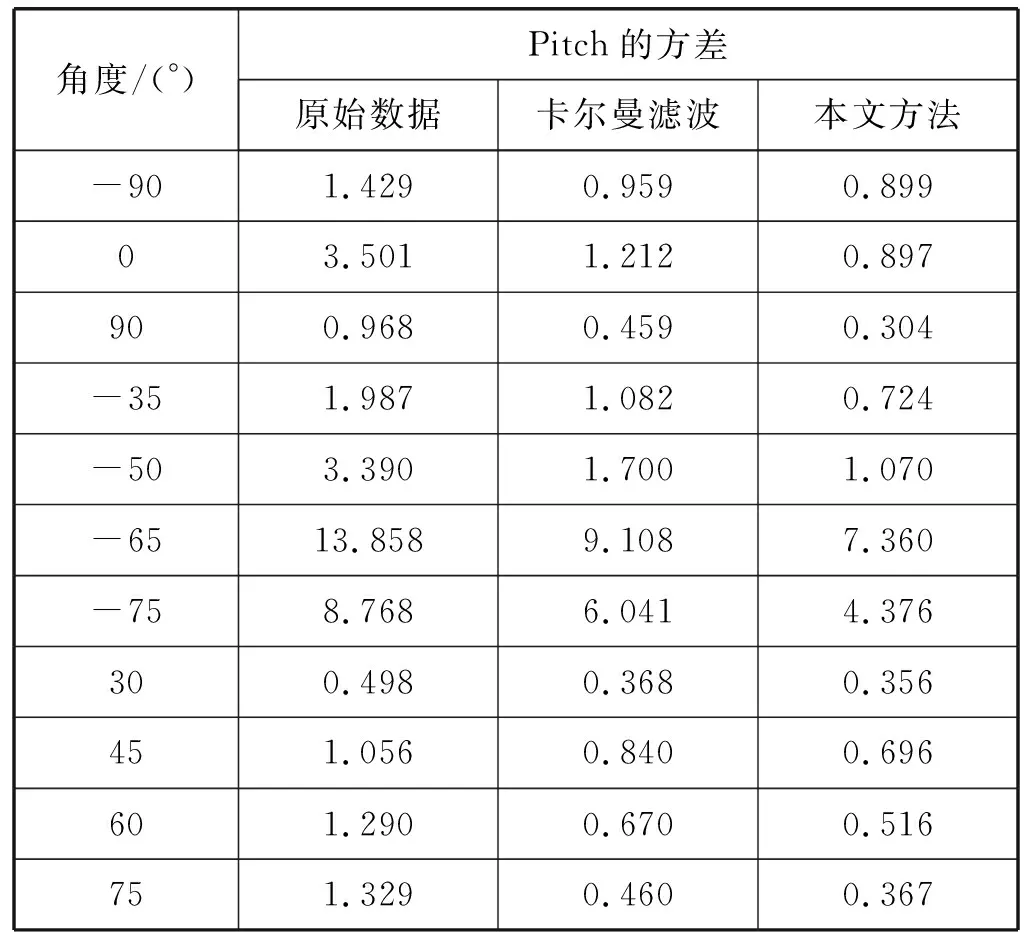
表2 不同方法滤波后Pitch的方差比较

表3 不同方法滤波后Yaw的方差比较

重复上述实验10次，得到欧拉角方差的平均值。表4列出了卡尔曼滤波和本文方法对原始数据方差减小的程度。可以看出，与卡尔曼滤波相比，本文方法对Roll、Pitch、Yaw这三个角原始数据的方差的减小程度更大，分别比卡尔曼滤波多减小11百分点、14百分点、15百分点，从而使欧拉角的稳定性更好。

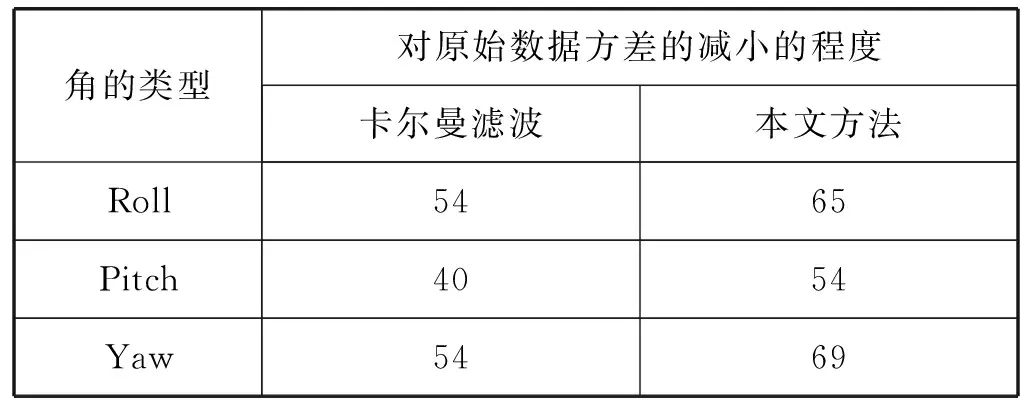
表4 不同方法对原始数据方差减小的程度比较(%)

本系统可以得到手在任何姿势下的角度，并将角度可视化到彩色图像上和OpenGL构建的3D手模型上，为了验证可视化效果，设计实验三如下：站在Kinect摄像头面前，旋转手，在彩色图像上绘制了一个与Kinect具有相同初始状态的坐标系，然后将计算得到的欧拉角传递给坐标系和OpenGL构建的3D手模型。实验三的结果如图4所示,图4展示了手旋转在一系列连续帧的彩色图像和OpenGL虚拟手模型上的估计结果，可以看出彩色图像中的坐标系和OpenGL构建的3D手模型都随手的旋转而旋转，能够准确地模仿手的旋转运动。由于本文方法是基于Kinect骨骼点的四元数进行手方向估计，Kinect的帧率为30帧/s，满足实时性要求。

图4 手方向估计结果

3 结 语

本文是基于Kinect的手方向实时估计系统。该系统利用Holt双指数平滑滤波算法平滑Kinect的骨骼数据，根据骨骼数据定位到手的位置。由于四元数旋转较复杂且不直观，该系统将四元数转换为欧拉角，但是在此过程中会出现奇异解问题，该系统通过设置合理的阈值的方法来解决，使得转换过来的欧拉角不会发生自由度损失。为了克服Kinect噪声对欧拉角的影响，该系统提出一种将卡尔曼滤波和中值滤波结合的算法。实验结果表明，与卡尔曼滤波相比，该方法能更有效地消除欧拉角中的噪声，使得欧拉角更稳定。为了验证系统的准确性和实时性，本文在彩色图像中对手方向进行估计，同时运用OpenGL建立了3D手模型，可以实时准确地模仿手的运动。但是该系统在手不是沿骨骼方向运动时对手方向估计不准确，因为会出现手掌平面将手腕点遮挡的情况，导致骨骼点不能定位到手腕点，因此，优化系统，使其能够解决此问题是下一步的研究方向。