钢-聚丙烯混杂纤维超高性能混凝土受压细观数值模拟

卢秋如, 曾彦钦, 胡煊

(1.武汉市青山区水务工程建设质量安全监督管理站，武汉 430080；2.武汉大学土木建筑工程学院，武汉 430070)

随着经济社会的不断发展，人民生活水平显著提高，但资源枯竭、环境污染、气候变暖等问题也日渐凸显，进行能源结构调整、重点领域减排刻不容缓。建筑行业全过程碳排放量巨大，已占到中国碳排放总量的50%，亟需构建绿色建筑技术体系，发展超低能耗建筑，对建筑规划设计、建造、使用、运行、维护等全过程进行低碳优化控制。

超高性能混凝土(ultra-high performance concrete, UHPC)是一种优良的绿色高性能混凝土，与传统的混凝土相比，UHPC一般采用两种以上的胶凝材料，提高组分的细度与活性，同时剔除粗骨料，使材料内部初始缺陷减到最少，在此基础上，掺入适量纤维，获得高延性与高韧性[1-2]。目前，向UHPC掺入纤维的方式有多种，包括单掺钢纤维、碳纤维[3]、聚丙烯纤维[4]、聚乙烯纤维[5]等，或者混合掺入前述两种纤维[6-10]。采用高弹性模量的钢纤维和低弹性模量的聚丙烯纤维混杂，可在不同层次和受荷阶段发挥阻裂作用，抑制和约束裂缝的开展，显著提高UHPC的延性。

目前多采用试验手段对钢-聚丙烯混杂纤维超高性能混凝土(steel-polypropylene hybrid fiber reinforced ultra-high performance concrete, HFR-UHPC)进行受压力学性能研究[11-13]，而HFR-UHPC是多相复合材料，成分复杂，内部结构具有随机性，是典型的非均质材料。数值模拟是在细观层面研究非均质材料力学性能和损伤演化的有效手段。基于ABAQUS建立HFR-UHPC细观数值模型，分析其力学性能的影响因素，研究其损伤演化过程，揭示纤维增强机理，具有重要的科学意义。

鉴于此，通过建立钢-聚丙烯混杂纤维超高性能混凝土三维细观数值模型，与前期轴心受压试验结果[14]进行对比验证模型的合理性。在此基础上，拓展分析纤维掺量、长径比等参数对超高性能混凝土受压特性的影响，揭示纤维增强超高性能混凝土的机理，从而为深入研究混杂纤维超高性能混凝土力学性能提供理论依据与参考。

1 HFR-UHPC细观数值模型

HFR-UHPC细观结构可细分为钢纤维、聚丙烯纤维、砂浆基体及纤维与基体的界面。研究表明，聚丙烯纤维对材料的宏观力学性能影响主要为闭合微观裂缝增加混凝土的韧性，而聚丙烯纤维非常纤细(直径仅0.048 mm)，在细观层次模拟非常困难。为简化建模并突出主要影响对象，将在基体中考虑聚丙烯纤维的影响，不单独建立聚丙烯纤维的数值模型。

1.1 钢纤维随机分布模型

HFR-UHPC中采用的钢纤维为细直型，截面形状为圆形。在同一试件中，规定投放的钢纤维尺寸相等，三维细观数值模型中钢纤维根数N计算公式为

(1)

式(1)中：floor()为MATLAB中向下取整函数；VSF、lSF和dSF分别为钢纤维的体积掺量、长度和直径，单位分别为%、m、m；Dc和Hc分别为试件的直径和高度，单位都为m。

为实现钢纤维位置和角度的随机性，采用常见的随机函数rand()，具体生成钢纤维随机分布模型的步骤如下。

步骤1生成3组分别在(0, 2π)、(0,Dc/2)和(0,Hc)区间均匀分布的N维随机数数组t1、r、Z1，则钢纤维第一个端点坐标可由式(2)确定。

(2)

步骤2对第一根钢纤维随机生成角度φ和θ，其中，φ为纤维与xoy平面的夹角，θ为纤维在xoy平面上的投影线与x轴的夹角，则钢纤维的第二个端点坐标由式(3)确定。

(3)

步骤3判断钢纤维的第二个端点是否满足下式的边界条件，若满足则储存第二个端点的坐标值；若不满足，则返回步骤2。

(4)

步骤4在试件区域内逐根生成所有满足条件的钢纤维。

雷区 FAR:基于比例因子,对凸包H进行相似转换所形成的区域为雷区FAR F。如果s和t是凸包H外的两个任意节点,且满足式(1):

步骤5输出所有钢纤维的端点坐标数据。

基于MATLAB软件，生成钢纤维随机模型如图1所示。

图1 钢纤维随机模型

1.2 钢纤维数值模型

利用ABAQUS软件进行数值模拟，ABAQUS可通过编辑输入文件实现前处理的二次开发。MATLAB中储存的钢纤维端点坐标可用于定义结点信息，通过结点编号可定义单元信息。输入文件导入的模型均为孤立网格，孤立网格不能进行网格重划分。因此，在输入文件中需要完成钢纤维的网格划分。考虑到钢纤维尺寸较小，根数较多，将钢纤维简化为三维桁架单元，单元类型为T3D2，网格尺寸为0.004 m。将输入文件导入ABAQUS中便可生成钢纤维几何随机模型，如图2所示。

图2 钢纤维几何随机模型

1.3 钢纤维材料参数选取

钢纤维采用双线性随动硬化模型，材料参数取值如下：弹性模量为200 GPa，泊松比为0.3，密度为7 800 kg/m3，屈服应力和极限拉伸应力分别为2 500 MPa和2 800 MPa，极限拉伸应变为0.1[15]。塑性硬化法则设置为“kinematic(随动)”。

1.4 UHPC基体几何模型及网格划分

将UHPC基体视为均匀的材料，单元类型选用C3D8R，网格种子大小设置为0.005 m，采用结构化网格划分技术。虽然基体的网格尺寸最好小于钢纤维的网格尺寸[16]，但是若将基体网格尺寸设置为0.002 m，基体网格总数将高达37.1×104，对计算机的物理运行内存要求将极高，高性能计算机都无法满足要求。因此，参考已有的细观数值模型研究结果[17]，经过试算，确定基体网格尺寸为0.005 m，能得到较好的模拟结果。

1.5 UHPC基体材料参数选取

采用混凝土塑性损伤模型模拟UHPC基体。损伤塑性模型需要输入单轴受压屈服应力-非弹性应变曲线、单轴受拉屈服应力-开裂应变曲线(或应力-裂缝宽度关系、断裂能)和5个塑性参数。

基于前期研究成果[14]得到HFR-UHPC单轴受压应力-应变模型，将模型进行退化得到单掺聚丙烯纤维的UHPC受压应力-应变曲线，减去相应的弹性应变得到屈服应力-非弹性应变曲线。关于受压损伤参数dc，参考文献[18]进行确定。

由于主要侧重于分析受压性能，所以对UHPC基体的受拉本构关系进行了简化，采用断裂能的方式进行定义，且忽略受拉刚度退化。根据单掺聚丙烯纤维UHPC三点弯曲试验结果[19-20]，将UHPC基体开裂应力取为5 MPa，断裂能取为1 600 J/m2。

参考文献[18,21-25]，将UHPC基体的5个塑性参数分别取为1.16、2.0/3.0、56°、0.1和0.000 5。

1.6 钢纤维与UHPC基体间的接触关系

基于已有微细观模拟结果[26-28]可知，钢纤维与超高性能混凝土基体之间的界面具有良好的黏结性能。因此，假定钢纤维和UHPC基体之间为理想黏结状态，不考虑两者的相对滑移，采用类似钢筋混凝土中绑定钢筋的方式约束钢纤维，在ABAQUS中提供的约束中选择“嵌入区域”，指定钢纤维为嵌入单元，UHPC基体为主体单元。

1.7 边界条件

对细观数值模型采用位移控制加载方式，对模型顶面施加沿z轴负方向的轴向位移，位移量为0.003 24 m。限制模型上边界沿xyz轴的转动和下边界沿xyz轴的平移和转动。

1.8 模型验证

基于前期试验研究成果[14]，将数值模拟计算结果与试验结果进行了对比分析。如图3所示，超高性能混凝土细观数值模型与试件破坏形态保持一致，均为剪切破坏形态。模型计算所得应力-应变全曲线与试验曲线[14]在下降段拐点前完全吻合，在拐点后模型计算的轴向应力略大于试验曲线的轴向应力，其原因是细观数值模型中没有考虑钢纤维的粘结滑移及拔出，钢纤维在峰后的桥接作用不会失效，能与基体共同承担轴向荷载，增大峰后残余应力。总体上，数值模拟结果与试验结果吻合较好，所建立的细观模型较准确。

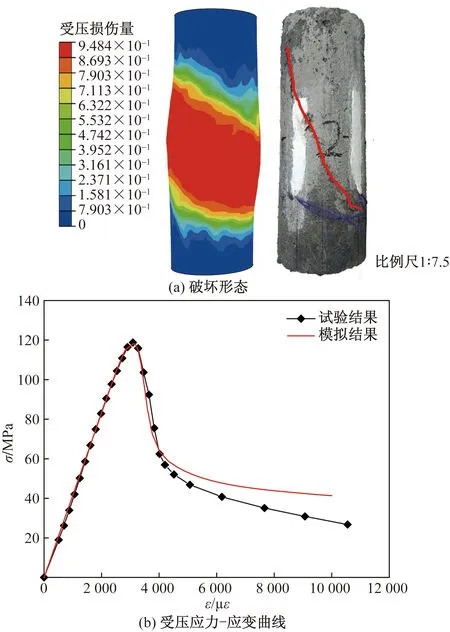
图3 HFR-UHPC数值模拟结果与试验结果对比

2 纤维参数分析

在验证了HFR-UHPC细观数值模型的基础上，扩展分析纤维特征参数对超高性能混凝土受压特性的影响。

2.1 钢纤维体积掺量的影响

当钢纤维体积掺量为零时，数值模型在中部发生了均匀膨胀，如图4(a)所示。这说明将超高性能混凝土视为均匀材料进行数值模拟时，难以模拟出真实的破坏过程。如图4所示，随着钢纤维体积掺量增加，超高性能混凝土横向变形逐渐减小。该结论与Hannawi等[8]进行的超高性能混凝土单轴受压试验结论一致。

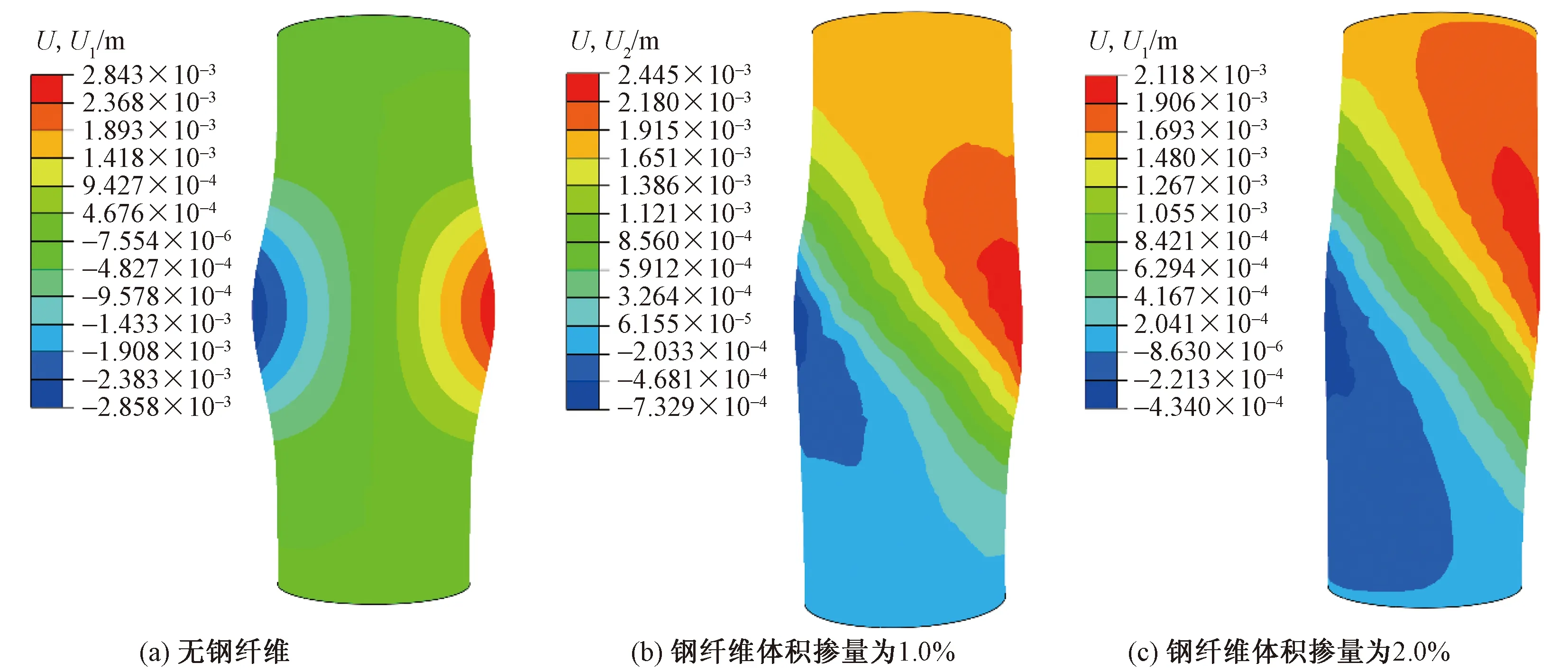
U为位移；U1为沿x轴的位移量；U2为沿y轴的位移量

图5为不同钢纤维掺量下超高性能混凝土基体的损伤云图。可以看出，随着钢纤维体积掺量增加，超高性能混凝土基体的损伤程度逐渐减小。由此可见，纤维能够有效抑制裂纹不稳定扩展和不连续裂纹相连，延缓微裂纹损伤演化，从而减小超高性能混凝土的横向变形。

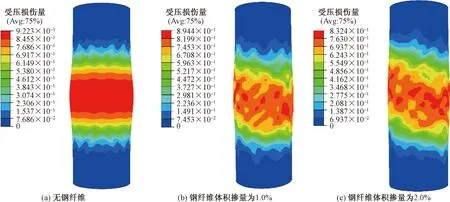
图5 轴向位移加载量为1.69 mm时UHPC基体的损伤云图

如图6所示，钢纤维体积掺量为1.0%的细观数值模型与不掺纤维的模型抗压强度基本相等，钢纤维体积掺量为2.0%的模型抗压强度比前两者略有提高；随着钢纤维体积掺量增加，模型峰值点后轴向应力下降更缓慢，具有更大的残余强度。

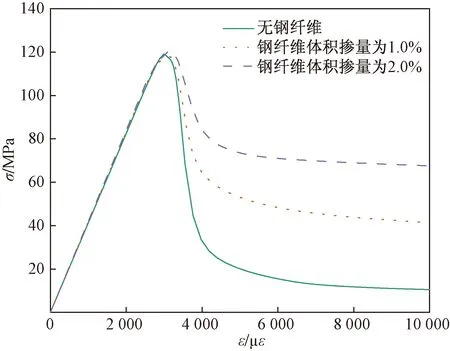
图6 钢纤维掺量对受压应力-应变曲线的影响

2.2 钢纤维长径比的影响

如图7所示，当钢纤维体积掺量为0.5%，长径比分别为30、60、80时，受压应力-应变曲线基本重合。分析其原因，一方面，随着钢纤维长径比增加，每根纤维桥接裂纹的能力增强；另一方面，钢纤维体积掺量保持不变时，钢纤维根数会随着其长径比增加而逐渐减小。相较宏观试验，细观数值模型试验条件更理想，不存在离散性，输出的是理论数值计算结果。受压应力-应变曲线是模型在单轴受压状态下的综合性宏观反映，“一增一减”的影响相互抵消，导致最终曲线基本重合。

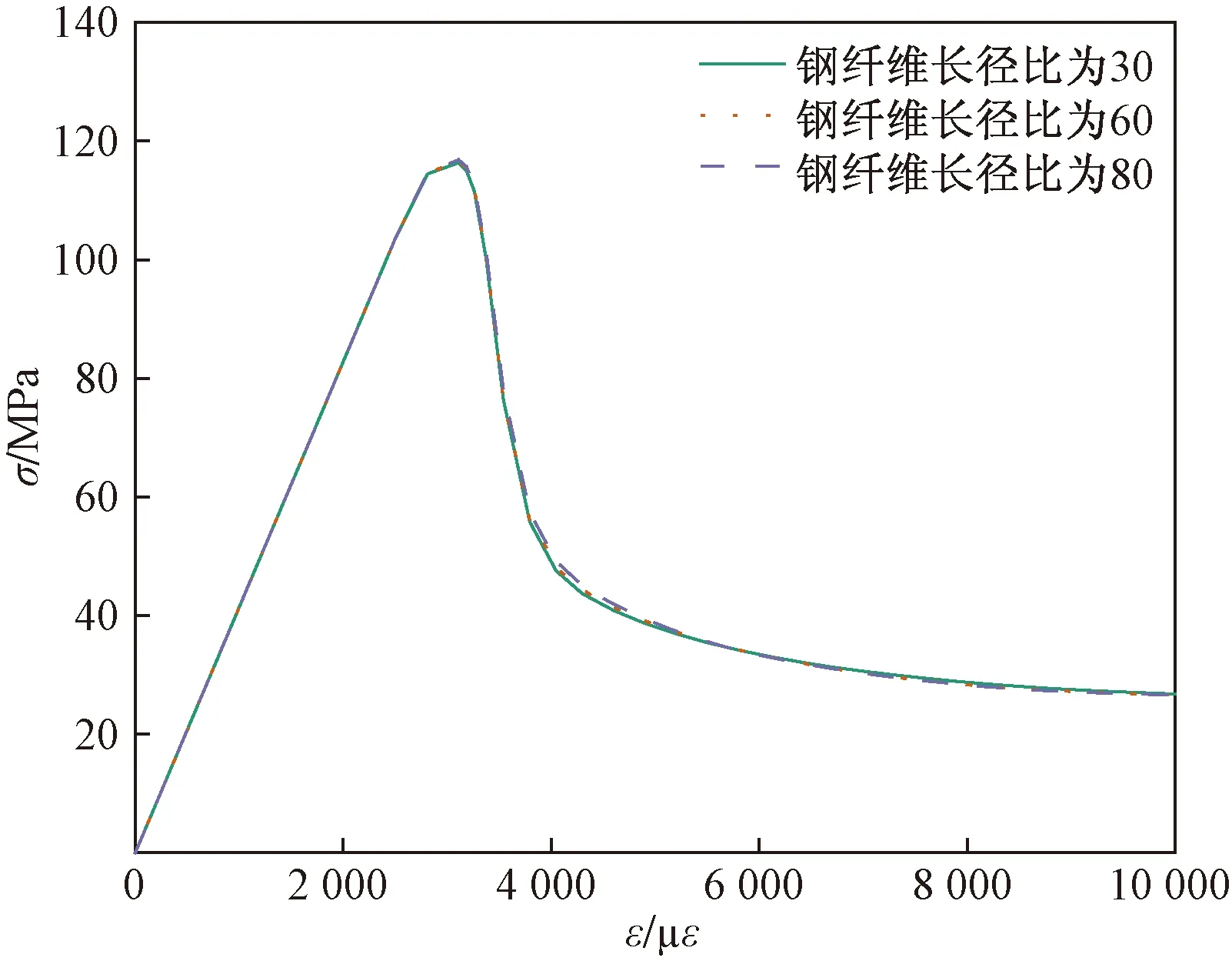
图7 钢纤维长径比对受压应力-应变曲线的影响

尽管如此，3个模型的破坏过程还是有所不同。如图8所示，钢纤维长径比为30的细观数值模型更早出现斜向损伤带，在终止加载时，斜向损伤带倾斜地更明显。纤维越短，桥接裂纹的能力越差，模型也更易形成宏观剪切斜裂纹。

图8 轴向位移加载量为1.78 mm时UHPC基体的损伤云图

3 纤维增强机理

结合试验[14]和数值模拟结果可知，在超高性能混凝土单轴受压过程中，纤维在不同阶段发挥了不同的增强作用：纤维在超高性能混凝土应力达到峰值点之前主要发挥骨架作用，之后主要发挥阻裂作用。

3.1 骨架作用

由于HFR-UHPC中掺入的钢纤维尺寸小，故钢纤维根数在较小的掺量水平下仍然很多，每根钢纤维之间的距离很小。这些钢纤维互相搭接形成三维空间网格骨架，如图2所示。通过细观数值模拟可得到峰值点前钢纤维Mises应力云图和超高性能混凝土基体损伤云图。如图9所示，超高性能混凝土基体在峰值点前损伤程度小；平行于轴向加载方向或者与加载方向夹角小于45°的钢纤维Mises应力值较大，钢纤维与超高性能混凝土基体共同承担轴向外荷载作用；而垂直于加载方向或者与加载方向的夹角大于45°的钢纤维Mises应力值很小，这些钢纤维不发挥作用。由此可知，在HFR-UHPC应力达到峰值强度之前，钢纤维主要与超高性能混凝土共同承担轴向荷载，发挥骨架作用。

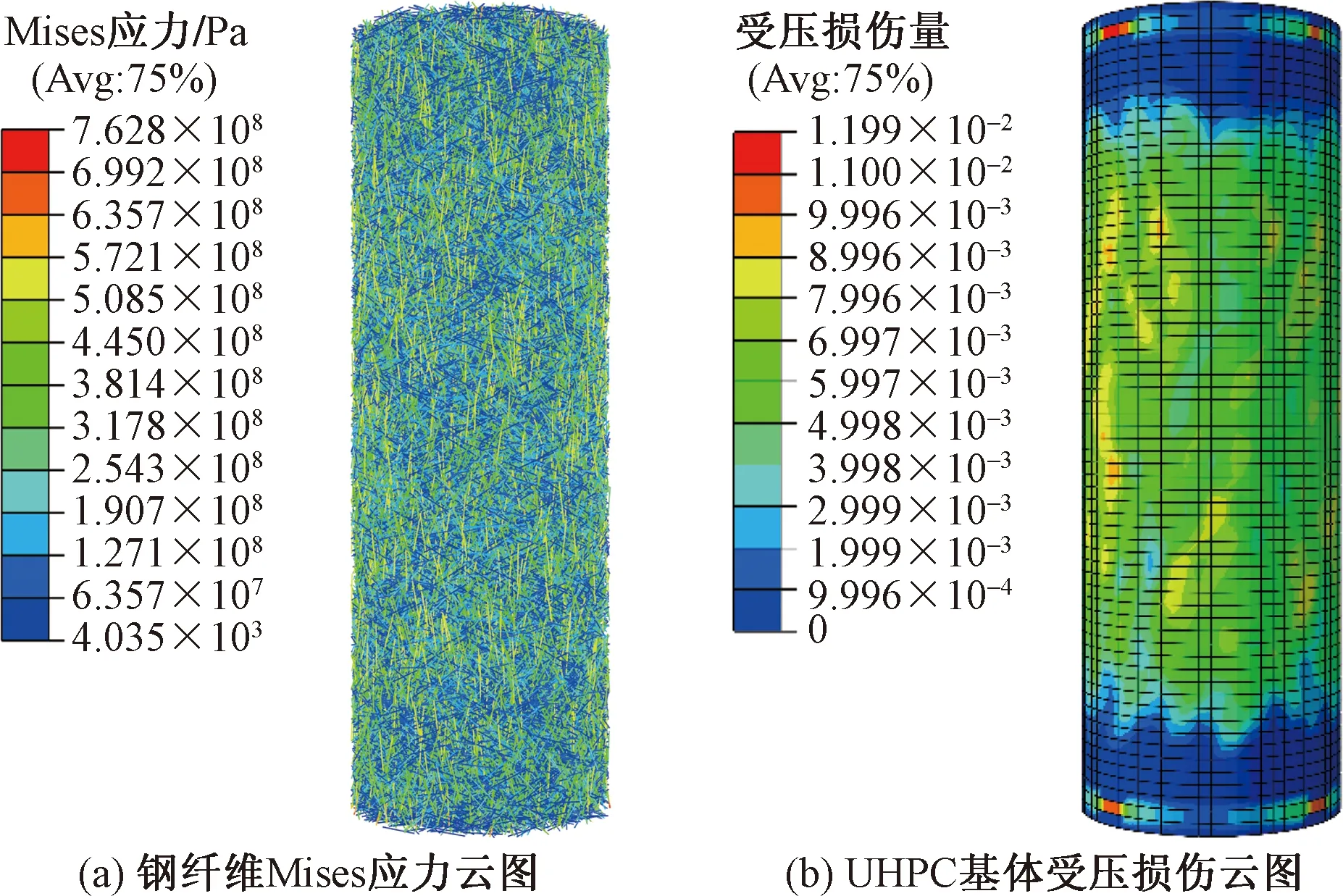
图9 峰值点前钢纤维Mises应力云图和UHPC基体损伤云图

基于前期研究成果[29]可知，纤维和基体界面的宽度主要取决于纤维直径。因此，相较于长钢纤维，微细钢纤维与超高性能混凝土之间的界面宽度更小。而且，超高性能混凝土具有极低的水胶比，使得钢纤维与超高性能混凝土基体之间的界面能够形成较多高密度水化硅酸钙和超高密度水化硅酸钙[26]。当超高性能混凝土中掺入了聚丙烯纤维，聚丙烯纤维能包裹住水泥水化颗粒，形成密实的网状体系，进一步增强钢纤维与基体间界面的化学粘聚力。从而保证钢纤维与超高性能混凝土基体能够共同受力与变形，让钢纤维充分发挥骨架作用。

3.2 阻裂作用

由于超高性能混凝土水胶比低，水分全部用于水化反应，并无多余的水分蒸发形成孔隙。掺入的硅灰和粉煤灰可与基体中的Ca(OH)2发生火山灰反应，提高水化产物质量和数量。未水化的颗粒也可作为“微骨料”增强混凝土基体[28]。超高性能混凝土中还剔除了粗骨料，消除了粗骨料与基体之间的薄弱界面。因此，与普通混凝土相比，超高性能混凝土的初始缺陷更少，不易开裂且裂纹发展滞后，钢纤维的阻裂作用在超高性能混凝土达到峰值强度后才逐渐发挥。

图10为峰值点后钢纤维Mises应力云图与超高性能混凝土基体损伤云图。可以看出，在超高性能混凝土基体中部有几处损伤程度较大，形成了斜向的损伤带，横跨这些损伤带的钢纤维的Mises应力值很大，说明钢纤维分担了部分基体开裂引起的拉应力，发挥明显的阻裂作用。对于钢-聚丙烯混杂纤维超高性能混凝土，与常规的超高性能混凝土相比，聚丙烯纤维的掺入能进一步增强钢纤维与超高性能混凝土基体的摩擦力[29]，使钢纤维在超高性能混凝土中能够更好地发挥阻裂作用，抑制裂纹发展，减弱应力集中，延缓混凝土破坏，提高峰后残余强度。

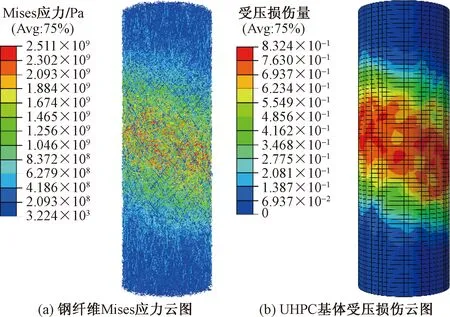
图10 峰值点后钢纤维Mises应力云图与UHPC基体损伤云图

4 结论

(1)建立含有钢-聚丙烯混杂纤维的超高性能混凝土细观数值模型时，可将聚丙烯纤维的作用考虑到基体中，以提高数值计算效率。将钢纤维与超高性能混凝土基体之间视为理想黏结状态，不考虑两者的相对滑移时，细观数值模型仍能准确地模拟出混杂纤维超高性能混凝土单轴受压时的破坏形态和应力-应变全曲线。

(2)随着钢纤维体积掺量增加，超高性能混凝土损伤发展变缓，单轴受压峰值强度略有提高，峰后延性明显增加；钢纤维长径比对超高性能混凝土受压应力-应变曲线的影响较小，但是更长的纤维能更好地发挥阻裂作用。

(3)在超高性能混凝土单轴受压过程中，钢纤维在峰值点前主要发挥骨架作用，在峰值点后主要发挥阻裂作用。