面向三维残缺点云图像的数据精简方法

尹金林，王春香，刘流，王齐超，潘杙成

(内蒙古科技大学机械工程学院，包头 014010)

随着逆向工程技术在各行各业得到广泛应用，其点云数据采集技术也得到了飞速发展。许多具有自由曲面的零件都可以通过采集点云数据获得。采集的点云模型能清楚地表达模型的表面细节，但是也会有冗杂数据。对于接下来的数据处理造成了不必要的数据计算和存储的负担，影响数据预处理的效率以及模型的曲面光顺性，为解决上述问题，就需要对采集数据中的冗杂数据进行精简处理。

中外学者对三维点云数据精简开展了大量研究。文献[1]通过基函数计算点云数据密度值，结合粗滤波和精去噪，保留了模型的细节。文献[2]将粒子群优化算法引入到传统的平均距离精简法中，提高了算法的精简精度。文献[3]对点云法向量特征进行估计后，利用K均值和高斯球聚类来简化点云数据。文献[4]提出了一种基于K近邻和聚类算法的三维点云简化方法，使用K均值算法将3D点云划分为簇，对每个簇执行熵估计以去除具有最小熵的数据点，以此达到数据精简的目的。文献[5]基于法向角的局部熵来作为点重要性的判别依据，通过删除最不重要的点并逐步更新向量和重要性值，直至达到用户指定的缩减率。以上早期对点云冗杂数据的精简主要策略是删除密集区域数据，无法做到较好的保留点云模型几何特征数据点，精简后模型的边界及特征容易失真。

对此，也有许多学者针对保留特征点的点云精简方法展开了研究，即在对点云数据进行有效精简时，同时保留模型原有的特征点。文献[6]对不同类型的点云数据采用不同的精简策略，通过整合特征点和非特征点，实现了精简的目的。文献[7]提出了一种基于最优邻域局部熵的精简算法，较好地保留了模型的特征数据点。文献[8]提出了一种基于共形几何代数的点云简化算法，该方法能有效地保留模型局部细节且总体误差也较小。文献[9]设计了一种自动递归细分方案来挑选代表点并去除冗余点，通过细算算法自适应地进行数据精简，保持原始边界的完整性。文献[10]提出了一种具有特征保留的分散点云精简算法，该方法对不同曲率模型的适应性较好，但计算效率较低。文献[11]提出了一种基于自适应邻域和局部贡献值的点云精简算法，按类别和贡献值对点云进行精简，更好的保留了模型原始面貌。文献[12]提出了一种基于修改后的模糊均值聚类算法，根据点云特征信息和简化参数简化点云。文献[13]利用ε-支持向量回归(ε-support vector regression，ε-SVR)算法的平坦度特性识别扫描线高曲率区域中的点，有效地检测锋利边缘附近的点且无需额外处理。文献[14]利用稀疏矩阵检测点云显著性，在数据精简后不产生表面空洞的情况下，保持了形状特征。

以上的研究大多是针对完整模型的精简方法，但在实际点云数据采集过程中由于模型表面反射，光线环境，操作技术，模型结构角度等限制，会导致采集数据缺失，形成孔洞。而在进行点云数据精简时，需要保留模型原始边界特征点及孔洞邻域特征，以保证精简后模型不失真和后续的孔洞修补处理。针对目前已有方法存在的不足，提出一种针对残缺点云模型数据精简方法，通过点云法向量夹角作为特征检测算子，然后利用欧氏距离搜索特征近邻数据点，完成残缺模型特征点的提取。以平均曲率作为数据精简阈值，实现对非特征区域数据的精简，最后将提取到的特征数据点与精简后的非特征数据点融合，从而完成针对残缺点云的数据精简。为后续对残缺点云的修补等技术处理奠定了基础。

1 边界及孔洞初始特征点提取

1.1 点云空间索引的建立

由于采集的点云模型数据量比较庞大，且在空间内没有明显的特征规律。通过建立空间拓扑关系，可以加快点云查询计算的效率。但激光扫描得到的点云数据，是三维空间，普通的二分树不能满足需求。而KD-tree(KD树)数据结构，常用于大规模高纬度数据索引。其数据检索方式，如图1所示，共有12个数据点(p1～p12)。首先根据不同方向上坐标的方差大小决定起始分割方向(检索方向选取x轴方向)，再按照该方向将数据从小到大排序，选取中值附近数据作为根节点，大于中值的数据p2，存储在右子叶；小于中值的数据p3，存储在左子叶，然后根据方差大小依次更新分割方向(y轴方向、z轴方向)，插入节点，直至所有点云数据包含在该树中。

图1 KD-tree数据索引方式

1.2 点云法向量计算

法向量的估计方法有很多，使用经典而简单的主成分分析方法[15]来估计法向量。通过KD-tree空间点云拓扑关系，对点云数据进行邻域范围查找。对所求点周围满足一定条件的邻域点进行局部微切平面拟合，以该点邻域确定的微切平面法向量作为该点的法向量的估计值。

对于点云中的点pi，(i=1,2,…,k)，及其k个近邻点，拟合平面F(n，d)由式(1)可得。

(1)

对方程中半正定协方差矩阵M的特征值分解，如式(2)所示，其最小特征值的特征向量是点p的法向量的估计值。

(2)

1.3 特征点的判别

一般在平缓区域内法向量夹角变化不明显，但在点云数据边界以及存在明显特征的区域法向量变化比较明显，如图2所示，在模型的角点、平滑区域、边界处法向量夹角各不相同。通过计算样点与其邻域内点云法向量的夹角，来进行特征点的提取。

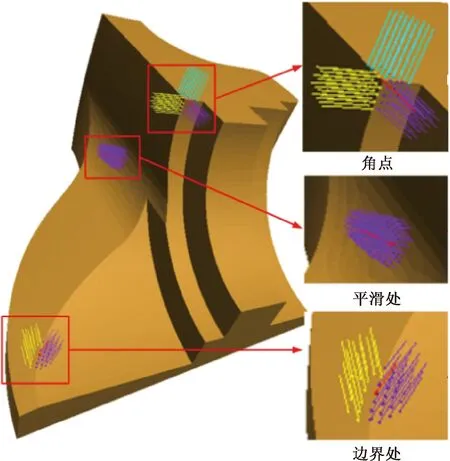
图2 模型不同特征处法向量夹角

记样点p1的法向量为n1(x1，y1，z1)，其邻域点p2的法向量为n2(x2，y2，z2)，两个法向量夹角由式(3)计算可得，从而得到样点与其邻域点法向量夹角的集合，将最大值αmax和设定的阈值ε比较，遍历全部数据。若αmax>ε，判断该点为边界特征点，并储存该点。反之舍弃该点，从而完成特征点初始特征点提取，其流程如图3所示。

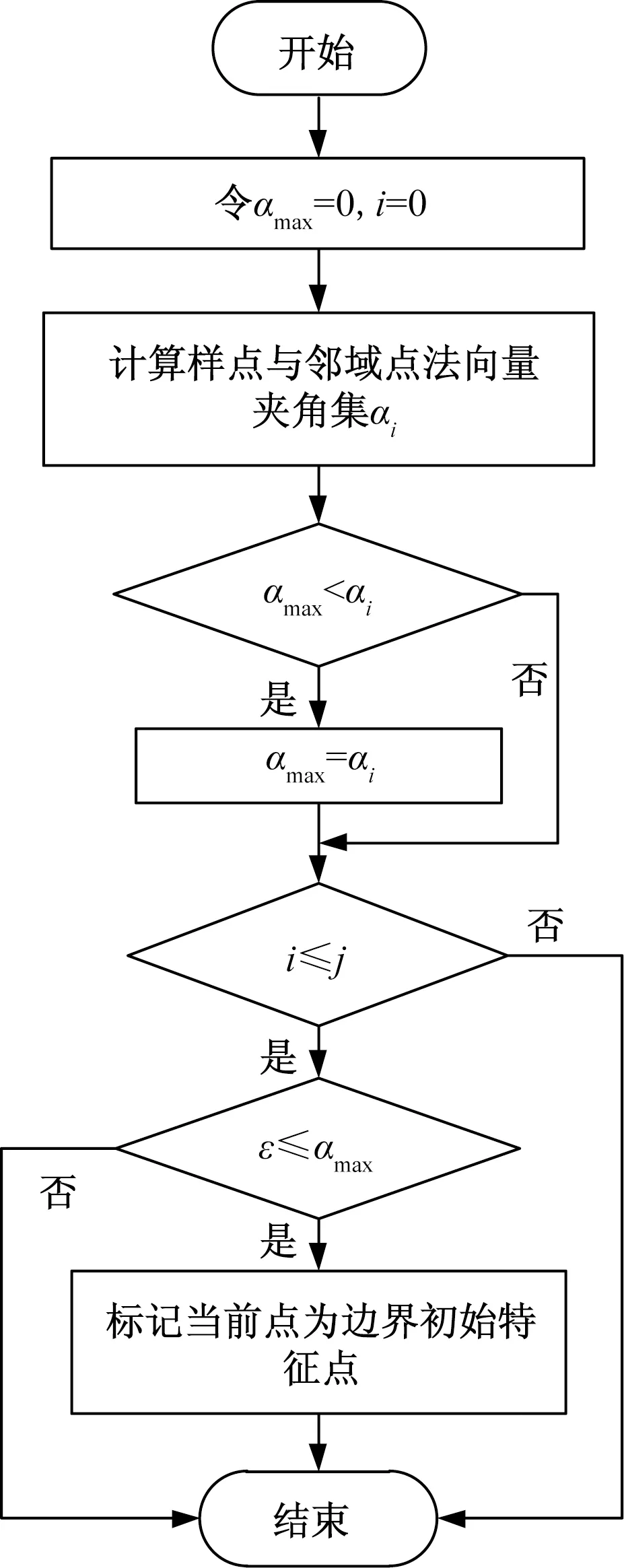
图3 初始特征点提取流程

(3)

采用上述方法对汽车翼子板、某汽车加强板、汽车保险杠外壳(部分)模型进行实验分析，其中，汽车翼子板共18 634个数据点，如图4(a)所示，由于数据采集时模型表面的反射造成的数据缺失。汽车某加强板件共126 128个数据点，如图4(c)所示，该模型原本就存在圆柱特征孔，但在数据采集时由于模型角度的限制，导致无法完整的采集到圆柱特征孔数据。汽车保险杠外壳共152 069个数据点，如图4(e)所示，该模型存在的特征较多，由于环境和操作的影响，在一些细小特征处造成了数据缺失。利用上述方法对以上模型进行特征点的初步提取，其提取的特征点如图4(b)～图4(f)所示。

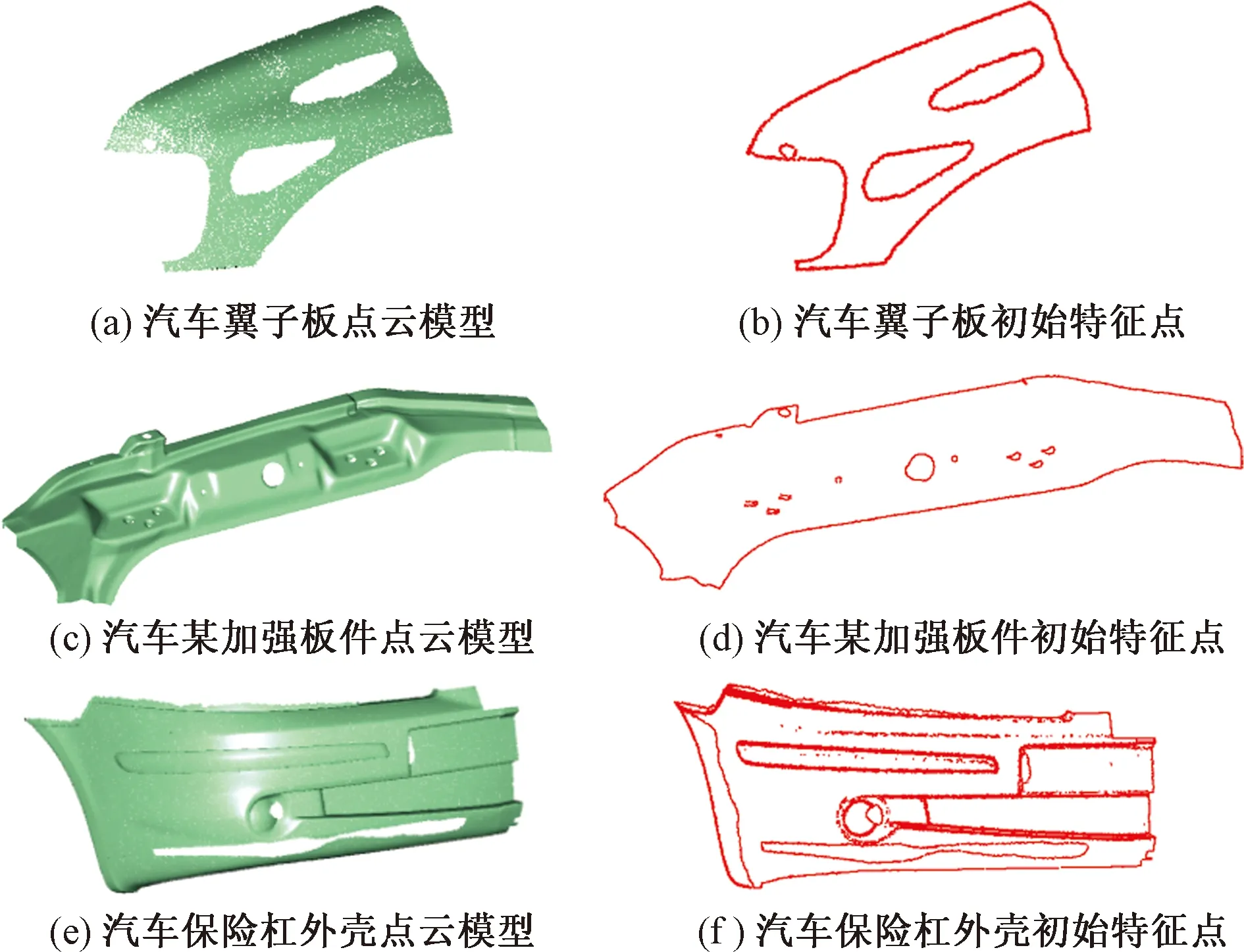
图4 点云模型及初始特征提取

2 边界和孔洞领域提取

通过给定一个目标点集(提取到的初始特征点)，利用点云数据与目标点集的欧氏距离搜索其最近邻，从而得到残缺点云的特征邻域点，使得提取出更多的边界特征数据。搜索最近邻域点数，其效果如图5所示，识别数据量如表1所示，把识别到的边界及孔洞邻域特征点云数据从原始数据中提取保存，以便接下来对非特征数据精简。

表1 识别结果数据量统计

KD-tree的最近邻搜索步骤如下。

步骤1在KD-tree中找出包含初始特征点的叶结点：从根结点出发，依次的向下访问。若目标点当前坐标值小于结点的坐标值，则移动到左子结点，否则移动到右子结点。直到子结点为叶结点为止。

步骤2以此叶结点为“当前最近点”。

步骤3递归的向上回退，在每个结点进行以下操作：①如果该结点保存的实例点比当前最近点距初始特征点更近，则以该实例点为“当前最近点”；②检查另一个子结点对应的区域是否与以初始特征点为球心、以初始特征点与“当前最近点”间的距离为半径的超球体相交。如果相交，可能在另一个子结点对应的区域内存在距离初始特征点更近的点，移动到另一个子结点。接着，递归的进行最近邻搜索。如果不相交，向上回退。

步骤4当回退到根结点时，搜索结束。最后的“当前最近点”即为初始特征点的最近邻点。

3 非特征数据精简

曲率是衡量弯曲程度的一个度量。传统的曲率精简法是一种全局性的精简方法，在数据精简时，根据点云平均曲率值的大小，在曲率变化较小的区域，保留较少的点，而在曲率变化较大的区域，保留更多的点。本文结合对边界和孔洞邻域特征的提取，对非特征区域数据进行曲率精简，以达到保留其特征的目的。

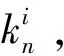
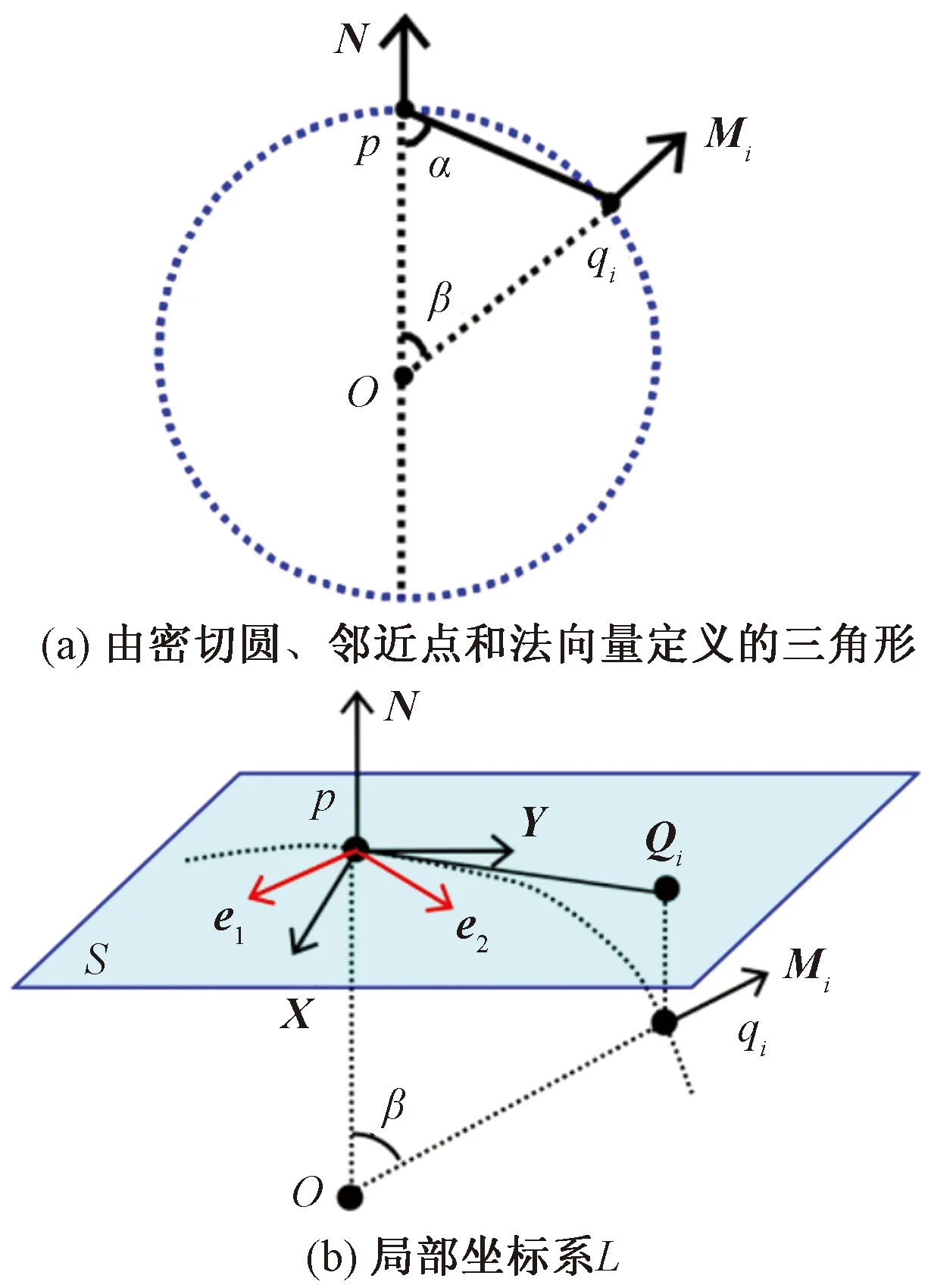
图6 变量的几何关系

(4)

式(4)中：α为向量-N和pqi之间的夹角；β为向量N和Mi之间的夹角。

式(4)的近似值可由式(5)得到。

(5)

设S是经过点p的平面，e1和e2是点p的主方向，对应的主曲率k1和k2都是未知的。未知参数θ为向量e1与X的夹角，θi为向量pQi投影到平面S上得到的向量X与向量pQi的夹角。根据欧拉公式，法曲率和主曲率的关系可表示为

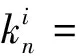
i=1,2,…,j

(6)

写成矩阵形式为

min‖Mμ-R‖2

(7)

式(7)中：

(8)

(9)

μ=[A,B,C]T

(10)

A=k1cos2θ+k2sin2θ

(11)

B=(k2-k1)cosθsinθ

(12)

C=k1sin2θ+k2cos2θ

(13)

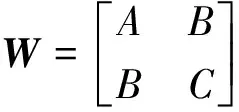
点云的平均曲率计算公式为

(14)

计算所有数据点全局平均曲率的平均值，计算公式为

(15)

将非特征点精简完成后的数据与提取到的边界以及孔洞邻域特征数据联合，从而得到精简后可以保留残缺模型特征数据的点云模型，其精简方法流程图如图7所示。

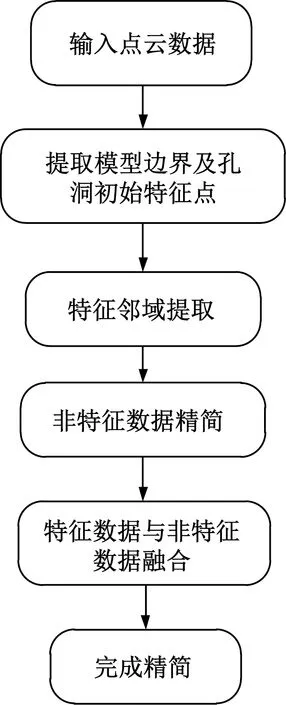
图7 精简方法流程图

4 实验结果对比

4.1 精简效果对比

对于残缺的点云模型，在数据精简过程中，更需要保持其特征数据，以便于后续的数据处理和曲面重构。为验证本文方法对残缺点云模型数据精简效果，基于点云库PCL以Visual studio 2017为平台，用C++语言实现以上方法，同时对某汽车薄壁类零件带有残缺的点云模型实现精简，并将结果与Geomagic Wrap软件中曲率精简法和随机精简法，进行对比。如图8～图10所示，采用随机精简法时，模型孔洞以及边界特征均有一定的失真。曲率精简法虽然保留了模型高曲率区域的点云信息，但模型孔洞以及边界特征数据信息丢失严重。而本文方法在对上述模型精简时，在顾及模型细节情况下，随着精简比率的上升，仍较好地保留了模型的边界特征数据。

图8 汽车翼子板精简效果

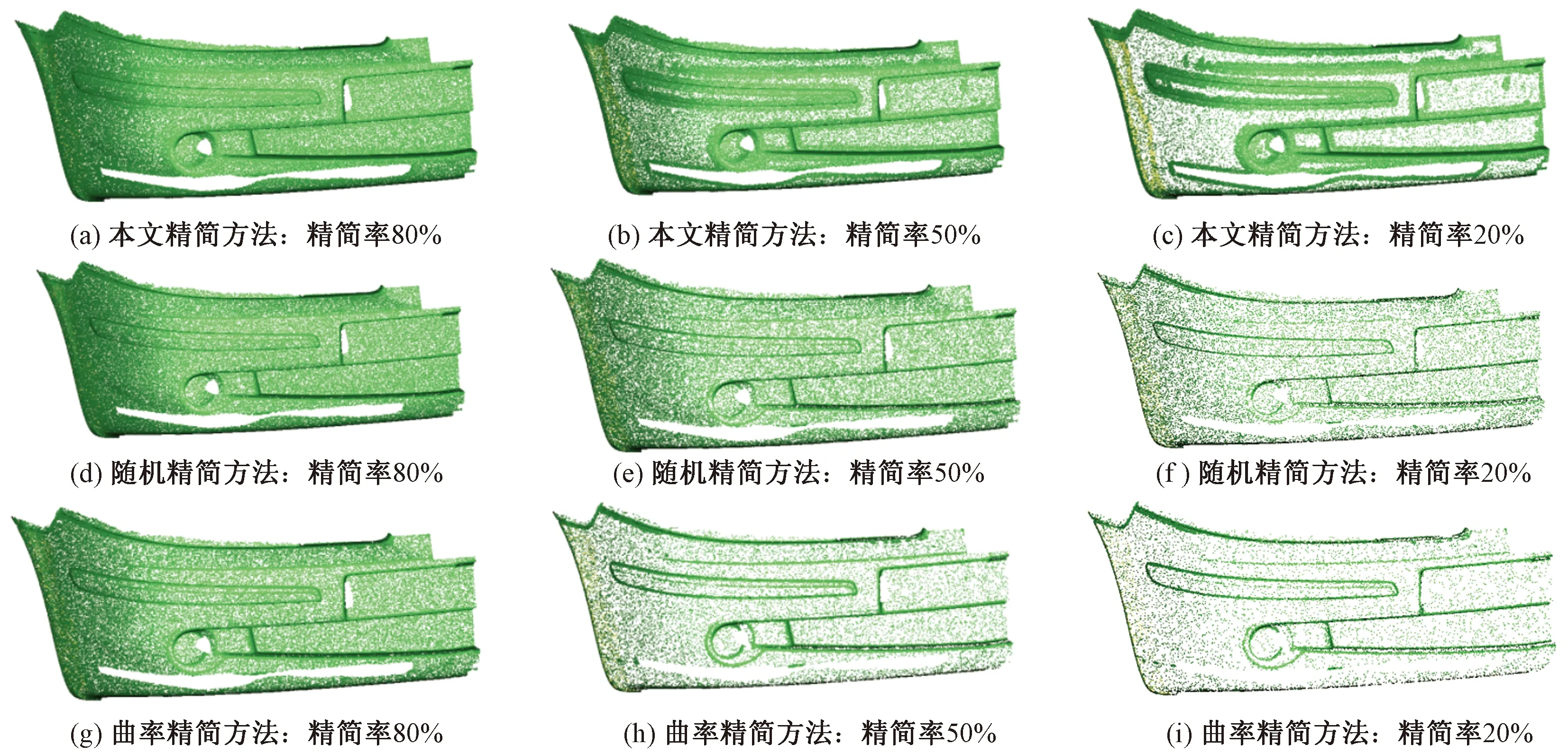
图10 汽车保险杠外壳精简效果

4.2 精简误差分析

为进一步评估本文精简方法，采用标准偏差和曲面表面积变化率对上述四个模型精简效果进行评价[17]。

标准偏差表达式为

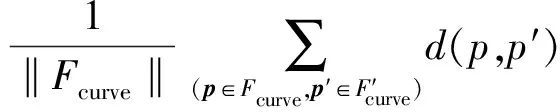
(16)

式(16)中：d(p,p′)为原始曲面Fcurve上采样点p到精简后点云曲面F′curve上投影点的欧氏距离，由p的单位法向量Np可知，d(p,p′)=|Np(p′-p)|。

表面积变化率的表达式为

(17)

式(15)中：Scurve为原始模型的曲面表面积；S′curve为精简后模型的曲面表面积。

如图11、图12所示，通过比较可以发现，总体上随着精简比率的上升，模型的标准偏差及表面积变化率也随之上升。但随机精简法通过随机删除数据点的方法精简，其精简效果具有不稳定性，标准偏差存在一定的波动；曲率精简法在对上述模型精简时，仅保留模型曲率较高的数据，对于较平坦区域的数据会造成丢失，精简结果并不佳，这也导致曲率精简法的表面积变化率高于其他方法。采用本文方法精简后的模型，其标准偏差和表面积变化率总体上大致处于均匀稳定状态且均优于其他方法，并保留了残缺点云模型的边界特征。

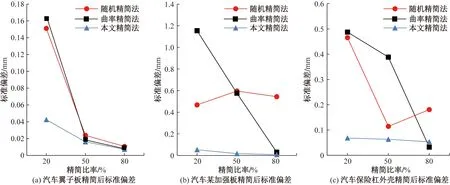
图11 模型精简标准偏差比较

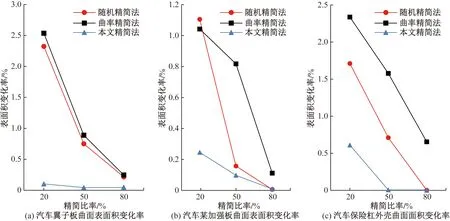
图12 模型精简后曲面表面积变化比较

5 结论

通过分析目前点云模型数据精简方法中的不足，利用本文方法进行实验验证，得出如下结论。

(1)针对薄壁类残缺的点云模型，提出了一种数据精简方法。利用法向量夹角选取初始特征数据点，借助欧氏距离搜索其近邻特征点，将模型数据点划分为特征数据点和非特征数据点，并对非特征数据点采用曲率精简的方法，实现局部数据的精简，最后，把精简的数据与提取的特征点合并，实现了一种保留其边界以及孔洞邻域特征点的数据精简方法。

(2)实现对非特征点最大可能精简又保证了边界及其孔洞邻域特征的不丢失，且精简后的标准偏差以及曲面表面积变化率优于其他两种方法。但本文方法在特征信息计算部分，仅提取到残缺模型的边界特征，针对残缺模型局部特征的提取值还有待进一步研究。