偏磨抽油杆接箍力学性能及承载能力分析
——以塔河油田抽油杆接箍断脱为例
康红兵,彭振华,丁雯,冯园艺,李京帅,李森*
(1.中国石油化工股份有限公司西北油田分公司,乌鲁木齐 830011;2.中国石油化工集团公司碳酸盐岩缝洞型油藏提高采收率重点实验室,乌鲁木齐 830011;3.东北石油大学机械科学与工程学院,大庆 163318)
目前,机械开采依然是油田开采的主要方式,全世界80%的油井是通过机械开采,在中国更是超过90%[1-4];在所有机械开采工艺中,有杆泵开采应用最多也最广泛,中外油田超过90%的生产井使用有杆泵抽油机进行地下采油[5]。抽油杆是有杆泵抽油系统的重要组分,连接着井口与地面,并起到动力和能量传输的作用。因此,抽油杆能否可靠运行是开采设备高效开采的关键。
塔河油田储层埋藏深,范围均在5 300~7 000 m,平均泵挂2 579 m;开采液黏度大,平均黏度为705.09 mPa·s[6],最大达到180×104mPa·s。这些因素都大大增加了抽油杆断脱的危险。为了改善这一状况,在开采工艺和设备选配方面做了大量工作,如对抽油杆材质筛选、抽油杆柱尺寸配备等。这些措施虽然对抽油系统安全运行有所改善,但抽油杆断脱依然是影响工艺开采的重要因素。并且在对抽油杆断脱统计中发现,其由接箍损坏占比很大[7],约为50%。通过对断脱抽油杆接箍对比分析发现,断脱的抽油杆接箍都出现不同程度的磨损。由于泵挂较深、开采液黏度较大、井斜角及开采过程中运行参数等因素存在,抽油杆接箍磨损不可避免。因此,开展抽油杆接箍受力分析及可靠性预测,可为采油系统杆柱结构设计和安全运行提供依据和参考。
为保证采油系统的可靠运行,许多学者针对抽油杆结构开展了实验测试和数值模拟分析,为新结构和新工艺的提出做出了大量工作。从材料的角度,Patil等[8]针对材料为35CrMo的抽油杆利用ABAQUS软件进行了轴向承载力的仿真模拟,从定性的角度揭示了抽油杆接箍断脱的原因。齐光峰等[9]论述了不同材料的抽油杆,在CO2与油井环境共同作用下进行实验,从而得出不同材料的腐蚀规律,为抽油杆的选材及寿命预测提供经验。王彦芳等[10]通过高速激光熔覆技术在抽油杆接箍上进行涂层,并通过各种实验对涂层后的性能进行验证,结果表明,涂层技术能大大提高接箍的耐磨性和耐腐蚀性。从抽油杆杆体受力角度,Romero等[11]利用有限元法对抽油杆接箍进行数值模拟,通过对抽油杆的受力分析,获得了抽油杆失效的主要原因。Villasante等[12]通过数值模拟,分析了有杆抽油泵的抗疲劳性能,间接的阐明了抽油杆失效的因素。许世航[13]建立抽油杆结构受力模型,并利用ABAQUS软件对模型进行分析,得出抽油杆与接箍连接螺纹的根部应力最大。Duan等[14]对断裂接箍试样微观样貌进行分析发现,偏磨和腐蚀是造成接箍损坏的主要因素,交变应力是次要因素。孙秀荣等[15]建立了一种位移激励下的屈曲模型,为抽油杆柱偏磨预测提供新的思路。Fan等[16]利用ANSYS软件建立模拟临界接触载荷方法,分析了最大杆柱应力与抽油杆直径和载荷的关系。张琴等[17]利用计算流体动力学(computational fluid dynamics,CFD)模拟方法得出抽油杆管柱的载荷分布规律,为防偏磨设计提供参考。根据现场调研、理论分析及数值模拟,部分学者从实验角度进一步验证抽油杆失效的使用情况。何文江等[18]通过对断裂面进行理化性能试验并对其金相组织分析,结果表明,腐蚀是导致抽油杆断脱的主要原因。Chacin等[19]通过API方法与实验相结合的方法,研究了稠油井杆柱受载荷的问题。
目前,众多学者多集中于对抽油杆柱整体使用寿命和杆体受力,以及涂层材料增强杆柱磨损方面的研究。缺乏对抽油杆接箍在不同偏磨量下的受力分析。为此,利用有限元法,开展考虑接箍壁厚受磨损程度的数值模拟,通过对不同轴向拉、压力下的等效应力及接触应力进行分析,并与实验结果进行对比,从而对不同磨损量下的抽油杆接箍寿命进行预测,以期为采油工艺的确定、采油抽吸参数确定和采取防断脱措施奠定基础。
1 抽油杆接箍力学模型
1.1 几何模型
建立抽油杆接箍三维模型,利用ABAQUS进行有限元分析,以直径25 mm抽油杆接箍为研究对象,由于抽油杆接箍螺纹螺旋升角较小,故不考虑其对载荷分布的影响。数值模拟将要考虑抽油杆接箍受偏磨后壁厚尺寸变化的影响,这里针对抽油杆接箍未受磨损、轻度磨损及严重磨损3种尺寸结构开展研究,具体结构和尺寸如图1、表1所示。

图1 3种状态下抽油杆接箍几何模型
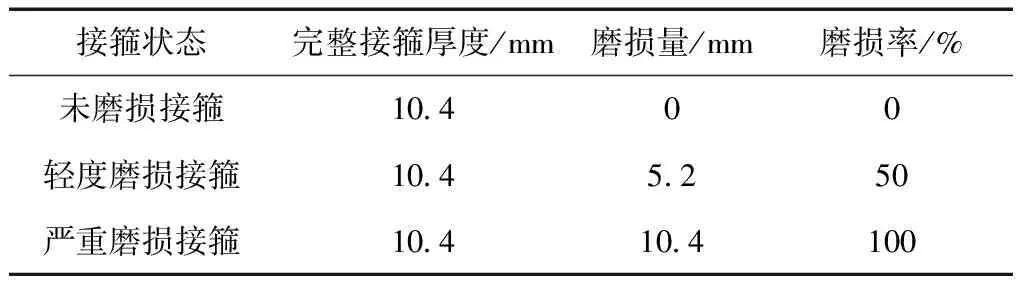
表1 模拟抽油杆接箍尺寸
1.2 数值计算方程
1.2.1 单元应变
由材料力学可得单元应变公式为
ε=Hf=HNδe=Bδe
(1)
式(1)中:ε为应变分量矩阵;H为微分算子矩阵;B为单元应变矩阵;f为单元内任意点的位移分量列阵;N为形状函数矩阵;δe为单元的节点位移分量列阵。
将所建模型看作抽对称可得局部坐标系ξ、η下其位移函数分别表示为
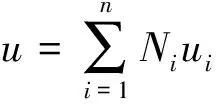
(2)
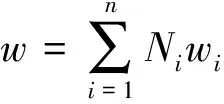
(3)
式中:n为单元节点数;u、w分别为沿x、y方向位移;Ni为单元形函数;ui、wi为节点位移。
转化为矩阵形式可表示为
f=Nδe
(4)
4节点形函数可表示为

(5)
式(5)中:ξ、η为平行于x、y轴的局部坐标系;ξi、ηi为局部坐标系上节点i的值。
8节点形函数可表示为
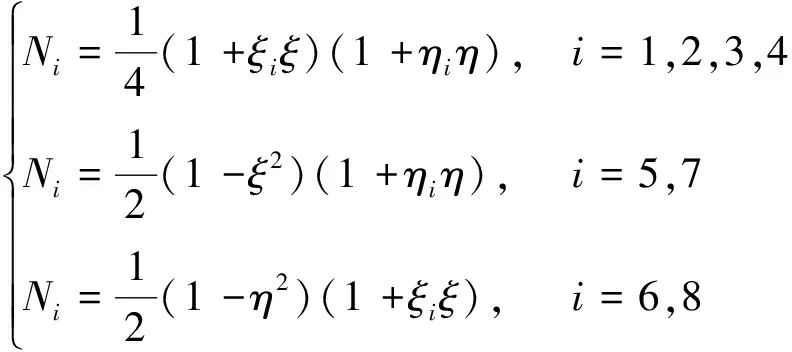
(6)
1.2.2 单元应力
由式(1)可得单元应力公式为
σ=D(ε-ε0)=Sδe+σ0
(7)
S=DB
(8)
σ0=-Dε0
(9)
式中:σ为应力分量列阵;D为弹性矩阵;S为应力矩阵;B为单元的应变矩阵;ε0为初应变分量列阵;σ0为初应力分量列阵。
1.2.3 单元刚度矩阵
设节点力为Fe,由虚功原理得
δ*eT=∭Vε*TσdV
(10)
式(10)中:δ*e为节点虚位移分量列阵;ε*为单元虚应变列阵;dV为微体积。
若无初应变则有
δ*eTFe=δ*eT∭VBTDBdVδe
(11)
化简可得
Fe=Keδe
(12)
Ke=∭VBTDBdV
(13)
式中:Ke为单元刚度矩阵。
1.2.4 单元等效节点力
若任意节点A(x,y,z)所受集中力为P,由虚位移原理得
δ*eTFe=f*TP
(14)
式(14)中:f*为A点虚位移分量。
化简可得单元等效节点力为
Fe=NTP
(15)
式(15)中:N为形函数矩阵。
同理可得单元受分布载荷Pl、分布面力Ps和分布体力W转化为单元节点力的方程为
Fe=∭VNTWdV
(16)
Fe=∬ANTPsdA
(17)

(18)
式中:A为单元面积;l为边界线段。
由式(16)~式(18)可得,不同载荷作用在单元内可转化为节点力方程为
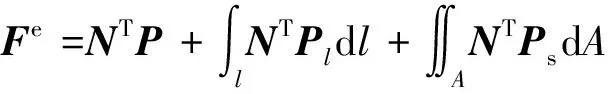
(19)
1.3 数值模拟材料属性
接箍材料为35CrMo,其常温下的力学性能参数如表2所示。

表2 35CrMo材料属性
1.4 网格划分
一般情况下,模拟结果的精度随着单元网格尺寸的减小而增大,但单元网格尺寸设置小到一定程度后,其不仅对计算结果精度增加量变小,反而会大大增加计算的数据量,所以在进行网格划分前进行网格无关性验证是十分必要的。图2(a)~图2(d)单元网格尺寸逐渐减小,可以看出,在相同的轴向拉力作用下,图2(c)、图2(d)图所示接头等效应力分布完全一致,4种网格尺寸下计算得到的等效应力结果如图3所示,可以看出,当计算所用网格尺寸较大时,从模拟所得数值可以看出结果相差很大,随着网格密度增加,计算结果相差逐渐减小,当采用图2(c)、图2(d)网格进行计算时,屈服拉力差值由模拟可知不到1%,同时,最大等效应力差值小于4%。鉴于计算数据量等原因,以图2(c)全局网格尺寸对抽油杆接箍模拟。

图2 不同网格尺寸刨面图与等效应力云图
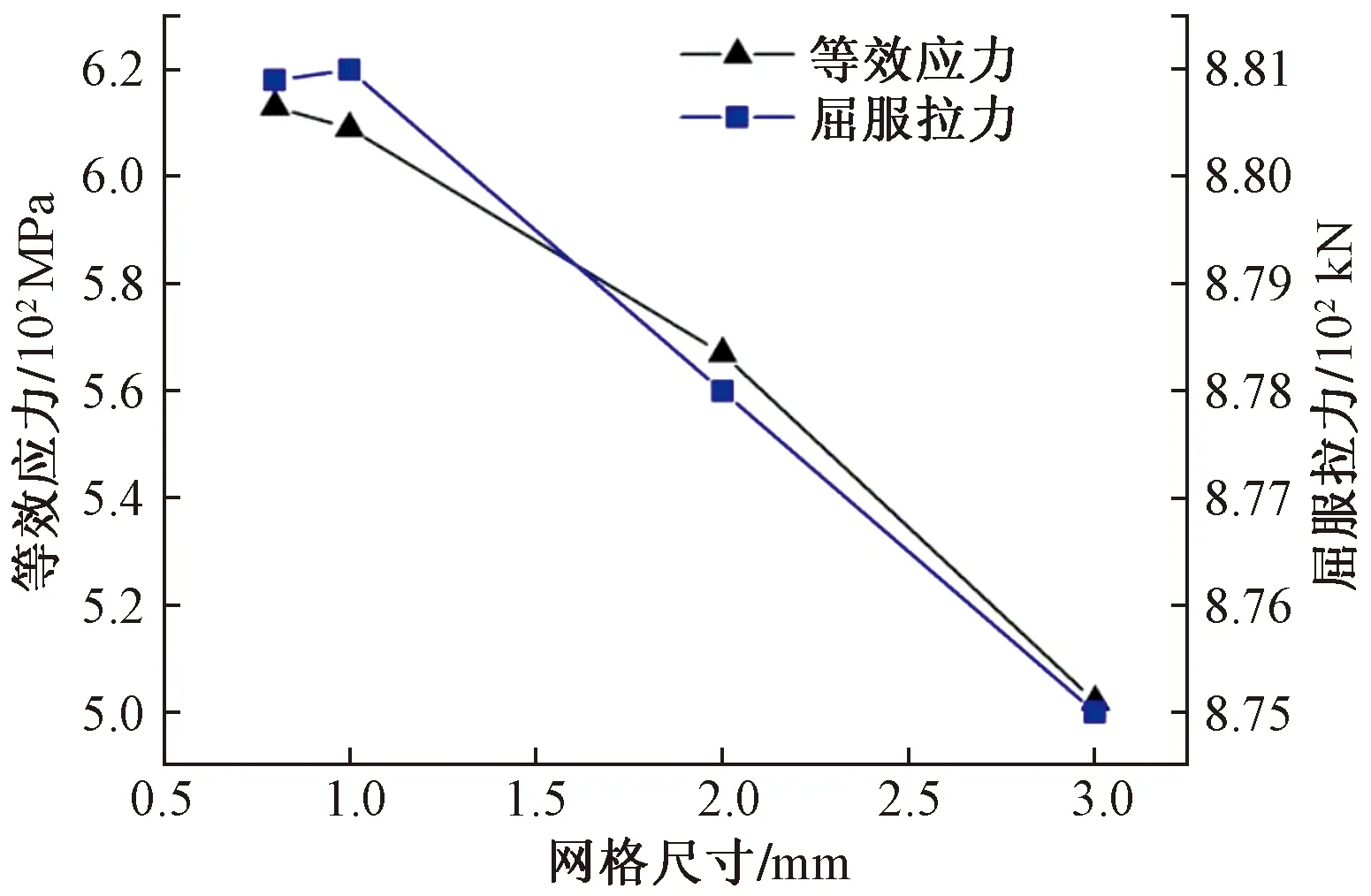
图3 不同网格尺寸及其模拟所得数据
1.5 边界条件
由于考虑抽油杆接箍受偏磨影响,在对抽油杆接箍进行受力分析时,需要限制接箍上部抽油杆的轴向运动及所建模型对称面垂直方向上的运动,然后对接箍下部抽油杆下端面施加轴向力,模型如图4所示。

图4 边界条件三维图
2 实验测试对比分析
为了验证数值模拟分析的可靠性,对同样结构尺寸结构开展了拉伸试验测试,试验测试载荷范围为20~80 MPa,图5为3种抽油杆实验图。

图5 3种抽油杆实验图
将实验所得数据与数值模拟所得数据进行对比,结果如图6所示。可以看出,随着拉伸载荷增大,数值模拟与试验测试的抽油杆接箍位移均在增大,无磨损和轻度磨损位移基本呈线性分布,而重磨损情况则偏移线性特性。数值模拟与试验测试结果基本吻合,最大误差为7.77%,可见所采用的数值计算方法是可行的。
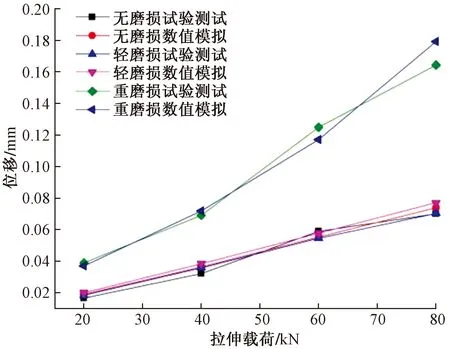
图6 不同载荷作用下实验与数值模拟位移曲线
3 讨论与分析
3.1 拉力作用下受力分析
图7~图9为Ф25 mm的抽油杆接箍,在不同轴向拉力作用下,未磨损、轻度磨损和重度磨损分别所受应力云图及其趋势。可以看出,抽油杆接箍的磨损对其承载能力有很大影响,当抽油杆接箍完好时,模拟数值显示接触应力和等效应力均低于材料的屈服强度且呈对称分布;当对轻度磨损的抽油杆接箍施加同等载荷时,由于受磨损抽油杆接箍的刚度下降,导致接箍的变形量增加,且其接触面之间的压力也相应增加,从而导致接触应力大于未发生磨损接箍,因此发生轻度磨损的接箍相较于未发生磨损的接箍更容易造成黏扣现象;而重度磨损的接箍其抗拉强度和抗粘扣能力均大幅下降,容易发生翘曲现象。当抽油杆的轴向载荷大于150 kN时,在接箍磨损量较大的位置会发生屈服现象,表明接箍失效。
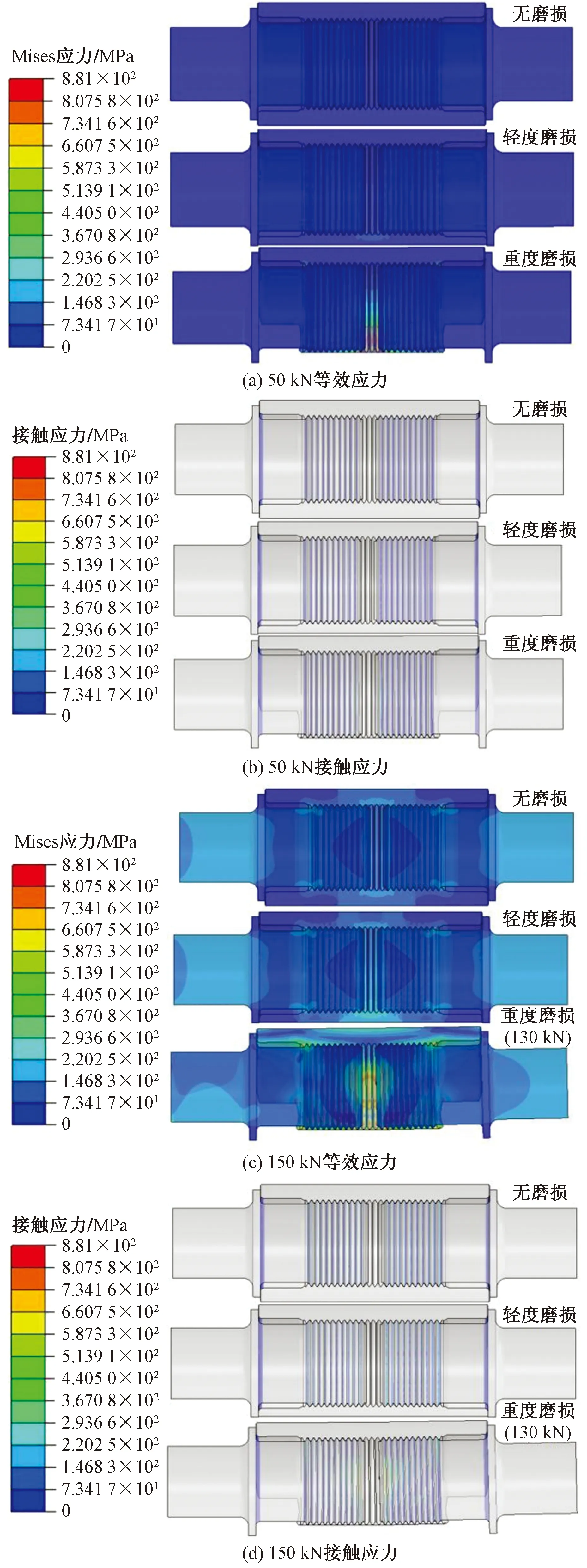
图7 不同拉力作用下25 mm抽油杆接箍不同磨损量应力分布
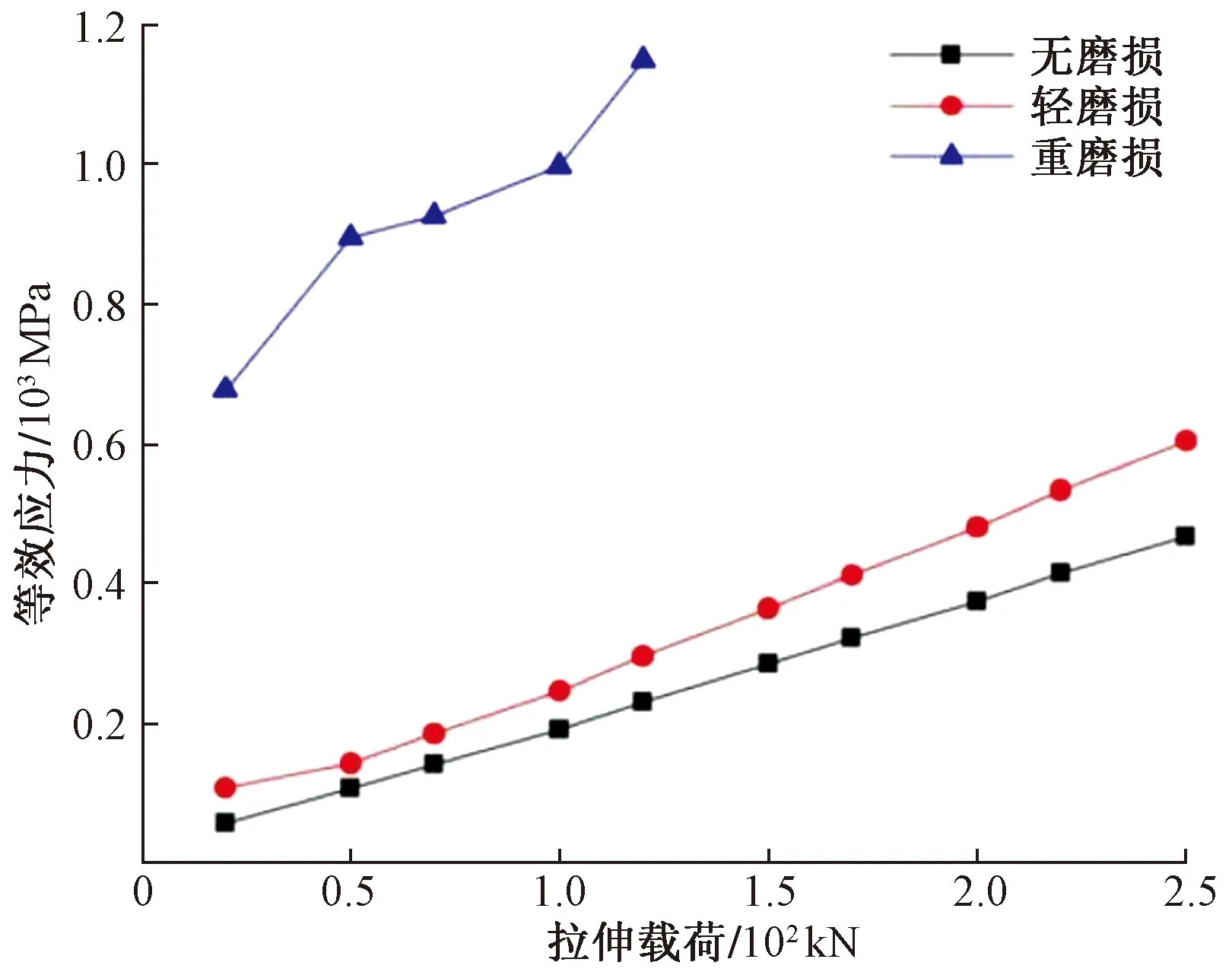
图8 不同拉伸载荷下最大等效应力曲线

图9 不同拉伸载荷下最大接触应力曲线
3.2 压力作用下受力分析
图10~图12为对磨损量不同的抽油杆接箍分别施加不同的轴向压力载荷,分析磨损量对接箍等效应力与接触应力的影响规律,可以看出,对未发生磨损的接箍施加20~250 kN的轴向压力,在载荷逐渐增大的过程中可以发现,未磨损的接箍,其等效应力和接触应力分布基本都呈对称分布规律,且其最大等效应力和最大接触应力也随着轴向压力的增加而增大,与此同时,接箍的整体等效应力和接触应力也会随着增加,当轴向压力达到100 kN时,抽油杆墩粗部分与台肩相连的倒角处的部分点等效应力值超过材料等效应力值,但屈服区域极小,无扩张趋势,且随着轴向压力的提升,屈服区域的等效应力值仅变化不足10 MPa,对于接箍的主体而言,其等效应力及接触应力皆位于材料屈服强度之下,说明Ф25 mm抽油杆接箍在未发生磨损时,其抗压能力是满足在井下环境使用要求的。
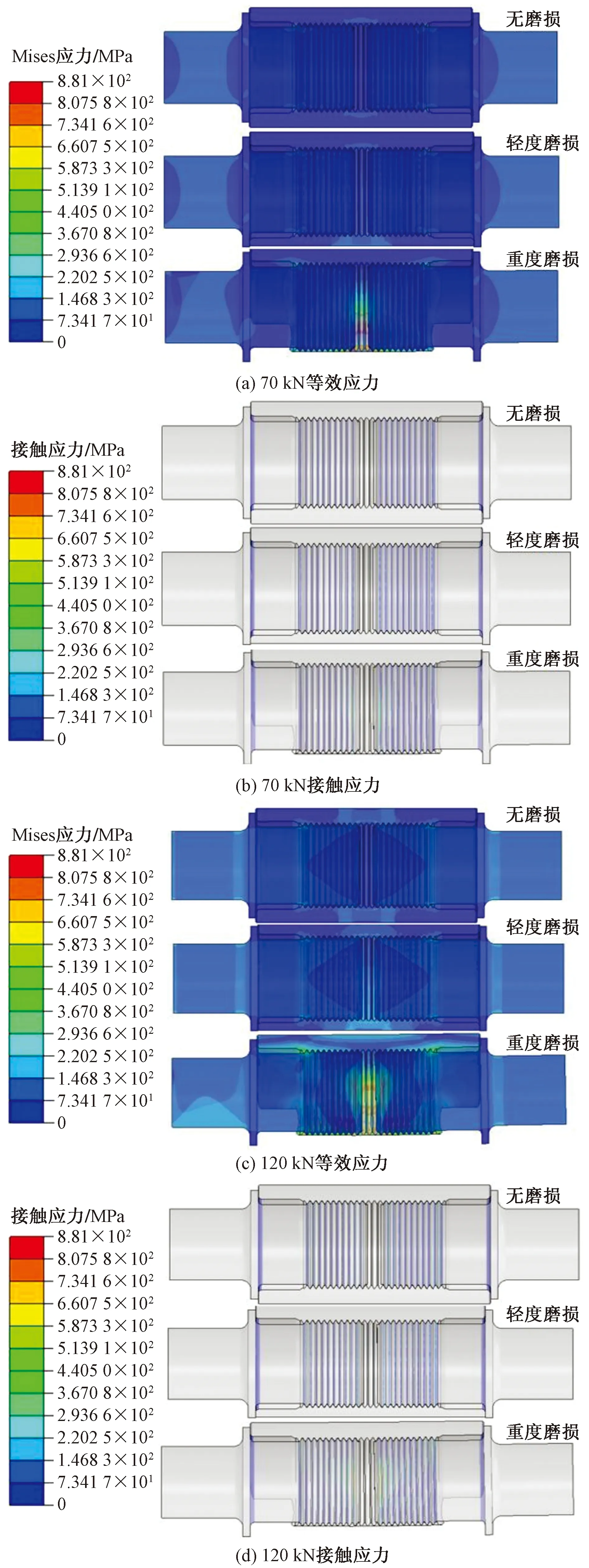
图10 不同压力作用25 mm抽油杆接箍不同磨损量应力分布
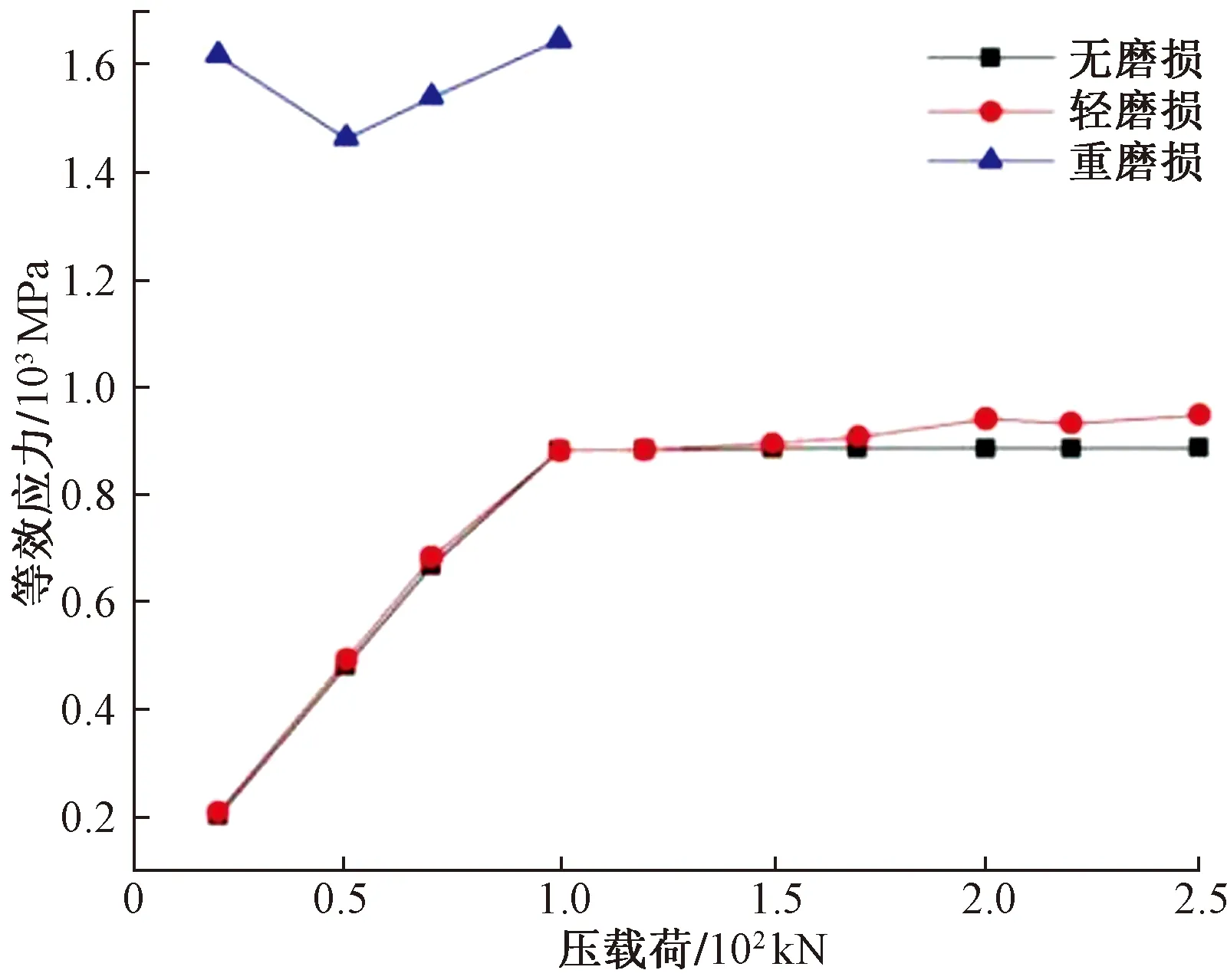
图11 不同压载荷下最大等效应力曲线
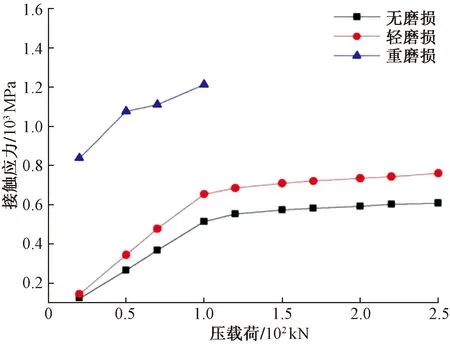
图12 不同压载荷下最大接触应力曲线
当Ф25 mm抽油杆接箍发生轻度磨损时,在对抽油杆施加的轴向压力小于170 kN的情况下,由图11 和图12可以看出,其等效应力随载荷的变化曲线和抽油杆接箍未磨损时基本相同,相差仅为1%,而当轴向压力超过200 kN时,发生轻度磨损的接箍等效应力水平超过未磨损情况的6.99%,这说明轴向压力过大时,发生轻度磨损的接箍其强度下降速度远超过未磨损接箍,并且相同轴向压力作用下,未磨损接箍的接触应力低于轻度磨损的接触应力,随着压力增加到250 kN,未发生磨损接箍所受的最高接触应力已低于轻度磨损的24.91%,因此表明,抽油杆接箍在受到磨损后刚度显著下降,在同等的轴向压力作用下,接箍的变形量明显提升。
当接箍发生严重磨损时,轴向压力达到60 kN时,接箍偏磨严重位置已经出现连续屈服,当轴向压力达到110 kN时,在接箍的薄弱位置会发生屈曲,当抽油杆上下往复运动的过程中,此位置会产生应力集中并导致裂纹产生,这种裂纹在反复的弯折应力作用下扩展并最终导致接箍疲劳断裂,由于25 mm的抽油杆使用位置在有杆泵井的中下部,受力环境以承压为主,故需要在偏磨严重的井段采取防偏磨措施。
4 结论
(1)当接箍未发生磨损且拉压载荷小于250 kN时,抽油杆接箍等效应力和接触应力分布均基本呈现轴对称分布,此时的等效应力和接触应力均低于材料的屈服极限,因此可以满足下井条件。
(2)当接箍发生轻微磨损时,其等效应力和接触应力随着轴向拉力和压力载荷的增加而逐渐呈不对称,此时表明,接箍磨损后其承载能力下降,相较于未磨损接箍,轻微磨损接箍更易发生黏扣现象。
(3)当接箍磨损较严重时,数据表明接箍的承载能力急剧下降,当拉伸载荷大于130 kN,压缩载荷大于110 kN时,接箍出现严重的屈服现象,并会在抽油杆循环载荷的作用下导致接箍的断脱。考虑25 mm的抽油杆使用位置在有杆泵井的中下部,承受压力为主,故需要在偏磨严重的井段采取防偏磨措施。

