液压驱动仿生捕蝇草柔性抓手的设计与实验研究

李健 王雨涵 王扬威 戴楚彦 栾智博

（1. 东北林业大学 机械工程学院，黑龙江 哈尔滨 150040；2. 哈尔滨工业大学 机械工程学院，黑龙江 哈尔滨 150006）

传统的刚性机械手已经被广泛应用在人类社会的生产生活中。随着生产要求的变化，传统刚性机械手所面临的工作任务愈加多样化和非结构化，逐渐难以满足工作需求，机械手逐步向着更加小型化、柔性化、可控易控的方向发展［1-2］。与刚性机械手相比，柔性抓手主体由柔性材料加工而成，可以极大地改变自身尺寸，具有很高的柔顺性、适应性和安全性，常被用在抓取易损物体、复杂环境探索以及医疗康复等场景［3-4］。

液压驱动柔性抓手由于具有驱动力大、刚度大、响应快等特点，受到了国内外学者的广泛关注，并得到了深入研究。如陈英龙等［5］设计的水液压驱动软体机器人、Galloway 等［6］开发的水压驱动的水下软体多指手、Polygerinos 等［7］研制的液压软体康复机械手、刘会聪等［8］提出的利用液态金属微流道应变传感器控制的软体机械手等。

常见的液压驱动柔性抓手一般采用手指、手掌分体式结构设计［9-11］，灵活度高，但对小型或碎片式物体较难完成抓取。文中参考捕蝇草的变形机理，设计了一种由双仿生叶片组成的液压驱动仿生捕蝇草柔性抓手，分析了单列、多列网格弯曲角度和压力的关系，确定了适宜的工作压力和准备压力，并通过适应性实验验证了样机抓取的稳定性，以期获得使用液压驱动稳定抓取的仿生捕蝇草柔性抓手，为安全稳定的无损抓取提供有效解决方案。

1 仿生叶片的结构设计与制备

1.1 仿生原理

捕蝇草（如图1所示）是一种能够实现快速响应的植物，其成熟植物细胞具有中心液泡，受到外界刺激后，会通过因渗透性吸水而肿胀产生的膨压改变细胞壁内的机械应力，实现快速闭合。捕蝇草由2个叶片组成，叶片内部有数根感觉毛，当昆虫第1次触碰到感觉毛时，捕蝇草叶片会进入“准备模式”，产生1个动作电位，导致膨压增大，叶片产生小幅缓慢弯曲。在此基础上，如果昆虫在短时间内再次碰到任意一根感觉毛，捕蝇草叶片将进入“工作模式”，产生第2个动作电位，使膨压进一步增大，叶片产生大幅快速变形，完成包裹式闭合［12-13］。

图1 捕蝇草Fig.1 Venus flytrap

1.2 结构设计与制备

文中所研究的捕蝇草叶片尺寸为20 mm ×11.5 mm，通过模拟捕蝇草的变形机理，将柔性抓手应用于实际生产工作中，结合在多个领域中柔性抓手的尺寸结构设计［14-16］，对捕蝇草尺寸做等比例放大5 倍处理（120 mm × 69 mm），以使该尺寸的结构可以有效抓取实际生活中的物品。由于昆虫在被捕捉时会剧烈挣扎，需要提供大而稳定的抓取力，而采用液压驱动能够更好地实现稳定抓取，因此文中设计的液压驱动仿生捕蝇草柔性抓手通过夹具固定2个仿生叶片构成，每个仿生叶片由限制层和变形层组成，其中变形层采用软体网格结构，按照矩形阵列排布，通过将水注入叶片网格中实现膨胀弯曲运动。根据捕蝇草类椭圆形的叶片结构，将仿生叶片的轮廓设置为长轴120 mm、短轴80 mm 的椭圆形，用距短轴上端点69 mm且平行于长轴的直线截取此椭圆形，得到的大面积部分为柔性抓手的叶片部分。将小面积部分优化为长方形的夹持部分，并将所得轮廓平面拉伸10 mm，得到图2 所示的仿生叶片，叶片的结构参数见表1。

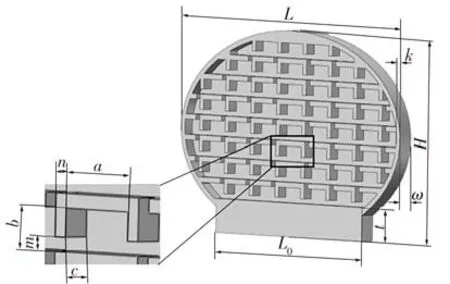
图2 仿生叶片的结构Fig.2 Strurcture of bionic blade

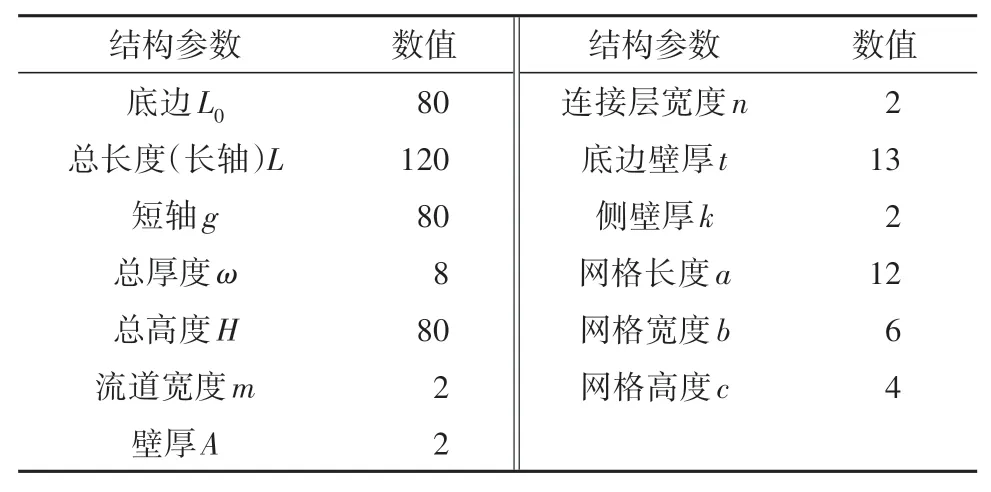
表1 仿生叶片的结构参数Table 1 Structural parameters of bionic blade mm

在限制层中加入较小伸长率的纱布，使仿生叶片在弯曲运动的过程中能够实现单向弯曲。使用同比例硅橡胶将限制层和变形层粘合，实现对捕蝇草叶片的仿生设计。使用FDM（熔融层积成型技术）打印技术制作模具，利用硅橡胶材料制备仿生叶片，制作流程与样机实物如图3所示。

图3 仿生叶片的制作流程与样机Fig.3 Production process and prototype of bionic blade

2 完全嵌入式网格的弯曲角度与压力关系分析

2.1 基于本构模型的单列网格分析

对材料的力学特性进行分析时，一般采用应变能密度函数描述力学性能［17］。考虑到硅橡胶材料的特点，选用适合于分析非线性、超弹性材料的Yeoh模型，其应变能函数如下［18］：

式中，W为应变能，C10、C20为应变能函数中待定的材料参数，I1、I2为变形张量中的2个不变量。

对使用的硅橡胶进行5组单轴拉伸实验，采用Matlab 中能够实现基于非线性最小二乘法拟合的lsqcurvefit 函数，将每组实验得到的应力、应变数据进行拟合，并将得到的5 组C10、C20材料参数取平均值，得C10=0.06、C20=0.01。

完全嵌入式单列网格见图4（a），可以将其看作由多个单独的网格线性排布而成。为控制仿生叶片的弯曲变化，首先应建立单列网格的弯曲模型，获得弯曲角度与压力变化的关系式。

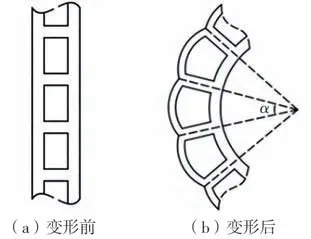
图4 单列网格形变图示Fig.4 Schematic diagram of the deformation of single-column grid

连接层、限制层和变形层受到的压力大小相同，但由于制作工艺和结构的区别，产生了不同的变形。由于连接层两侧受到同样大小的压力，因此只发生拉伸形变；限制层因受到纱布的限制，只发生小幅可以忽略的弯曲形变；而变形层会在单向压力作用下变形成以R为半径的圆弧，如图5（b）所示。单个网格的变形角为α，网格列中网格的个数为i，设每个网格的弯曲角度相同，则总弯曲角度θ=iα。变形层弯曲后的圆心角为β，将5个单个的网格一字排布以模拟单列网格弯曲，并通过Abaqus仿真得出中间网格α和β的数值关系，经多次仿真后取平均值，得β= 3α。

图5 单个网格形变图示Fig.5 Schematic diagram of the deformation of a single grid

在图5（b）所建立的坐标系中，变形层圆弧坐标可以表示为

根据几何关系可得

当压力增大时，网格发生膨胀，变形层和连接层发生形变，导致壁厚变薄，由于变形层与连接层受力大小相同，且变形层截面积是连接层的两倍，故变形层的主伸长量是连接层的两倍，所以根据几何关系可得主伸长量λ1如下：

变形层变形后的长度d通过几何关系表示为

因此，要得到压力p与弯曲角度α之间的关系，就需要得到p与β之间的关系。假设压力从0 增加到p，这个过程中侧壁上每一点的变形也线性增加到y（x），则侧壁上各点压力对侧壁所做的功可以表示为

故应变能密度可表示为关于β的函数：

变形层变形后的变形能可表示为

根据能量守恒定律，变形层上各点压力做功等于变形层整体的变形能，则有

联立式（1）-（8），即可计算出单列网格弯曲角度θ与压力p的关系：

2.2 基于仿真模型的多列网格分析

为减少软体驱动器制作时的工作量，使用能够更好实现超弹性分析的Abaqus 作为仿真平台。由于仿生叶片夹持部分不发生形变，故根据简化了夹持部分的仿生叶片结构建立仿生叶片变形的仿真模型［4］。在忽略重力与摩擦力影响的情况下，通过完全固定底面限制柔性抓手移动，采用静力、通用分析步并开启几何非线性选项，对柔性抓手内部封闭的网格赋予不同压力并逐个求解，得到图6所示不同压力下仿生叶片的变形状况。

图6 不同压力下仿生叶片的仿真结果Fig.6 Simulation results of bionic blade at different pressures

通过仿真得到图7 所示的仿生叶片弯曲角度。可以看出：当压力超过0.040 MPa后，仿生叶片的弯曲角度增加量逐步减小，且仿生叶片限制层处的压缩形变和连接层处的拉伸形变十分明显，网格过度膨胀导致的非理想变形也不断增大，严重影响仿生捕蝇草的工作稳定性，因此，将仿生叶片的工作压力定为0.040 MPa。

图7 仿生叶片的弯曲角度Fig.7 Bending angle of bionic blade

仿生叶片中矩形阵列分布的网格可以看作多个单列网格的组合，当单列网格中每个网格均完整时，多列网格的纵向弯曲角度等于单列网格的弯曲角度，但为保证仿生叶片边缘变形平滑，将侧壁与网格的距离始终固定，仿生叶片边缘必然会有数个不完整的网格，如图8 所示。在计算柔性抓手中每一列网格的弯曲角度时，将大于3/4 体积的网格按1 个有效网格计算，大于1/2 且小于3/4体积的网格按照1/2 个有效网格计算，未满1/2 体积的网格不计算在内。在计算有效网格数后，将横向相邻的2 个单列网格弯曲角度取两者的算数平均值作为整体的弯曲角度。通过这种计算方式，得到仿生叶片多列网格在压力作用下弯曲角度变化规律的理论关系。

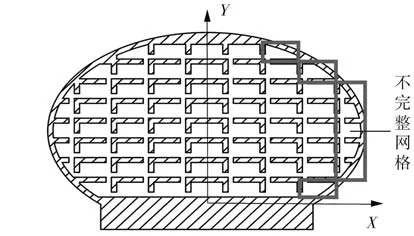
图8 不完整网格图示Fig.8 Schematic diagram of incomplete grids

基于图8建立的坐标轴，对工作压力下仿生叶片中第一象限各网格的角交点弯曲角度进行测量，建立如图9所示的弯曲轨迹图。

通过分析图9可知：1）长方体的网格布置导致柔性抓手的纵向弯曲角度远大于横向弯曲角度，而纵向弯曲角度的增大也会限制横向弯曲角度，使柔性抓手完成包裹式抓取；2）在纵向单列网格中，完整网格列中每多1个网格，弯曲角度就增加8°~9°，变化较为均匀，而不完整网格处的弯曲角度增幅显著增大，这会导致不完整网格处的受力大于完整网格处，故制作时需保证柔性抓手不完整网格内部的连接性能；3）在纵向弯曲变形中，底层厚度为2 mm，弯曲角度为13°，而网格的边缘厚度为1 mm，每个网格的弯曲角度增加量为8°~9°，对比可知纵向弯曲角度中的底层处弯曲角度过大，分析其原因，可能是因为底层厚度与网格边缘厚度不同会影响边缘限制条件，使实物与仿真的弯曲角度出现较大偏差。

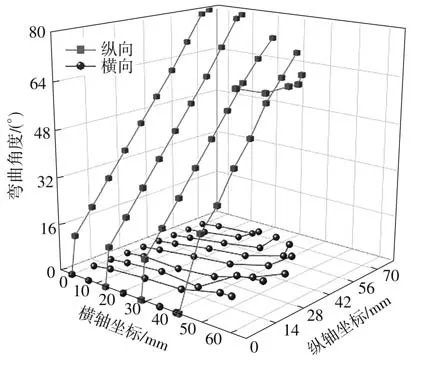
图9 弯曲轨迹图Fig.9 Plot of bending trajactory

3 实验与测试

为了对柔性抓手结构设计和仿真内容进行验证，进行以下3 组实验：①弯曲实验——对比液压与气压驱动仿生叶片的弯曲变化，并结合仿真和理论计算进行分析；②闭合力测试——对比液压驱动与气压驱动仿生捕蝇草机械手的闭合力，确定准备压力；③适应性实验——使用不同形状与质量的物体，对液压驱动柔性抓手的抓取能力进行验证。

3.1 弯曲实验

将仿生叶片安装固定，使用导管将仿生叶片、压力表和KKTS-24S18A 步进电机蠕动泵依次连接，通过液压与气压两种不同方式控制，记录不同压力下仿生叶片弯曲角度的变化，实现了如图10 所示的弯曲实验。

图10 弯曲实验Fig.10 Bending test

由仿真、理论计算与实验结果的对比（见图11）可知，仿真与理论计算的弯曲角度基本相同，液压与气压的实验结果趋势基本相同，证明了理论计算的正确性，其中最大弯曲角度的仿真值为75°，理论计算值为77°，液压驱动时为80°，气压驱动时为65°。相对于仿真结果和理论计算结果，液压驱动时最大弯曲角度的误差分别为6.30%和3.75%，气压驱动时的误差分别为15.40% 和18.50%。出现这些误差可能是因为软体执行器的实际结构参数和设计的参数存在一定的误差，实验条件无法与仿真中设置的边界条件完全一致，比如忽略了硅橡胶受重力的作用、硅橡胶浇铸存在缺陷等。在0.040 MPa的工作压力下，液压驱动的误差小于气压驱动，选用液压驱动的最大弯曲角度增加了23.10%。其原因可能是液压驱动仿生捕蝇草叶片内水的质量远大于气压驱动叶片中空气的质量，当弯曲角度较小时，这种重力引起的差别不明显，但随着弯曲角度增大，重力的影响也随之增大；当然，也可能是因为液体的压缩比小于气体。

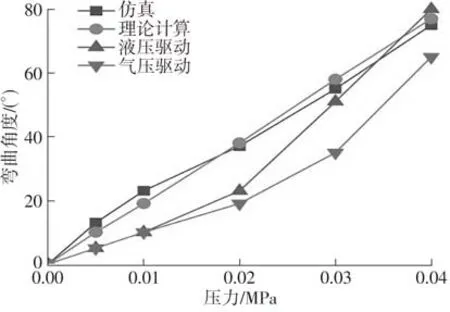
图11 仿真、理论计算与实验结果的对比Fig.11 Comparison of the results among simulation， theoreti⁃cal calculation and test

3.2 闭合力测试

为充分验证柔性抓手的闭合能力，进行了图12所示的闭合力测试，通过PU 管（气动压力软管）将仿生叶片、液压表和液压泵依次连接，并将仿生叶片与水平放置的测力计推力端接触，将测力计示数归零。通过PU 管将仿生叶片、液压表和液压泵依次连接，利用液压表读取不同压力值，并使用测力计 读 取0.005、0.010、0.020、0.030、0.040、0.050 MPa下的闭合力数值。

图12 闭合力测试实验Fig.12 Test of closed force

如图13 所示，随着压力的增大，闭合力也不断增大，在压力为0~0.010 MPa时，两种驱动方式均未对测力计产生推力，压力超过0.010 MPa 时，两种驱动方式下的闭合力均快速增长，所以将准备压力设置为0.010 MPa 能够快速提供闭合力。在0.040 MPa 的工作压力下，液压驱动时的最大闭合力为2.08 N，相比于气压驱动时的1.31 N 提高了58.8%，证明液压驱动的柔性抓手具有更优异的性能，能抓取更重的物品。

图13 不同压力下的测力结果Fig.13 Test results of force at different pressures

3.3 适应性实验

仿生捕蝇草的设计理念是设计一种能够稳定抓取物体的柔性抓手，对不同类型物体抓取的适应性，是衡量柔性抓手性能的重要指标。为了验证液压驱动仿生捕蝇草的抓取稳定性，进行了适应性试验，依次对表2所示的物品进行抓取。在抓取的过程中不断增大柔性抓手的压力，达到压力上限前，所抓取的物体未脱落，则视为能够稳定抓取。

表2 所抓取物品的参数Table 2 Parameters of the captured items

仿生捕蝇草柔性抓手对图14 所示松散（见图14（a））、球形（见图14（（b））、长条形（见图14（c））以及扁平类型（见图14（d）、14（e））的物体均有可靠的抓取稳定性，证明了被抓取物体的形状不会限制柔性抓手的抓取能力。实验测得柔性抓手的最大负载能力为304.3 g，并且具有比较大的上升空间。

图14 适应性实验Fig.14 Compatibility test

4 结语

文中提出了一种由双仿生叶片组成的液压驱动仿生捕蝇草柔性抓手结构。首先基于本构模型分析了完全嵌入式的单列网格弯曲角度与压力的关系，基于仿真模型分析了完全嵌入式的多列网格弯曲角度与压力关系，以及仿真与实物弯曲角度出现偏差的原因，为多列网格的软体网格结构的设计与分析提供了一定的理论参考。随后，模拟了捕蝇草的快速反应机制，通过仿真和闭合力测试，确定了0.010 MPa 的准备压力和0.040 MPa的工作压力。对仿生捕蝇草叶片进行液压和气压驱动的弯曲对比，结果表明，在工作压力下，仿真最大弯曲角度为75°，理论计算值为77°，验证了理论计算的正确性，液压驱动时的最大弯曲角度为80°，气压驱动时的为65°，液压驱动时的最大弯曲角度相比气压驱动时增加了23.1%。文中还对仿生捕蝇草柔性抓手进行了闭合力测试，发现液压驱动时的闭合力相比气压驱动时提高了58.8%，证明液压能够提供更大的负载能力。最后对液压驱动的仿生捕蝇草柔性抓手进行适应性实验，验证了柔性抓手的抓取稳定性，最大负载能力达304.3 g。文中结果为仿生植物机器人的研发提供了理论和技术基础，后续将致力于进一步提升仿生捕蝇草柔性抓手的抓取能力。