对流层增暖热带放大现象:基于FGOALS-g3 的模拟研究
刘士嘉 周天军 江洁 左萌 巫明娜
1 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室(LASG), 北京100029
2 中国科学院大学地球与行星科学学院, 北京100049
1 引言
大气是地球气候系统的重要组成部分,正确认识大气温度垂直廓线的长期变化趋势,对于理解气候变化成因至关重要(Steiner et al., 2020)。作为人类活动的主要区域,对流层内不同高度上的气温变化趋势受到科学界的广泛关注(Lindzen and Giannitsis, 2002; Santer et al., 2017a)。近20 年来,气候学界一直致力于使用气候系统模式模拟对流层大气温度的历史变化,模式对不同高度上大气温度变化趋势的模拟能力是气候模式研发领域重点关注的问题(Santer et al., 2005, 2008; Fu et al., 2011; Po-Chedley and Fu, 2012)。
器测资料揭示的全球平均地表温度自1880 年以来显著增高,增幅约为0.85°C,且记录中的最暖时段出现在近30 年(Santer et al., 2017b)。基于湿绝热过程的基础理论,热带地区的湿绝热过程会放大地表的增暖幅度,在约200 hPa 高度上产生增暖峰值,这种现象被称为“热带对流层放大”(Stone and Carlson, 1979)。热带对流层放大是21 世纪气候变化的显著特征之一。水汽、气温递减率以及云反馈等物理过程,在很大程度上受到热带对流层温度及其垂直结构变化的调控。因此,热带对流层放大现象对于大气环流变化以及气候敏感度均有重要影响。能否合理再现热带对流层放大现象,是评估气候模式模拟性能的重要指标,模式模拟和观测结果的差异及其成因,是科学界关注的热点问题(Fu et al., 2011; Po-Chedley and Fu, 2012;Santer et al., 2017b)。
全球变暖背景下,多套观测资料均揭示热带地区对流层中高层的增温幅度大于低层(Steiner et al., 2020)。研究表明,大多数气候系统模式高估了气温趋势放大率,即气候系统模式模拟的热带对流层高低层增温趋势之比明显大于观测结果,这一偏差在第三次和第五次“国际耦合模式比较计划”(Coupled Model Intercomparison Project,CMIP3/5)的模拟结果中均存在(Santer et al., 2005, 2008,2017b; Po-Chedley and Fu, 2012)。例如,针对1979年以来的热带对流层增温现象,Fu et al.(2011)通过比较CMIP3 耦合模式历史模拟试验与卫星观测资料的结果,发现耦合模式模拟的增温趋势强于观测,并认为这是导致模式模拟的热带对流层上下层静力稳定度变化与观测不同的主要原因。基于CMIP5 耦合模式历史模拟试验和单独大气模式试验(即“AMIP”模拟试验)也得到类似的结论(Po-Chedley and Fu, 2012)。
造成模式模拟与观测差异的因素包括:(1)气候模式外强迫资料的误差(Solomon et al., 2011;Santer et al., 2017a);(2)模拟和观测的海表温度趋势分布型(Tuel, 2019);(3)气候系统内部变率(Santer et al., 2019);(4)空间垂直权重函数对卫星资料反演的影响(Santer et al., 2017b)。例如,耦合模式的历史模拟试验中海洋与大气自由耦合所产生的气候系统内部变率难免与观测不一致,使得内部变率导致的温度变化掩盖外强迫的信号,从而导致耦合模式结果与观测结果在温度趋势上存在差异。相比之下,在观测海温驱动的单独大气模式试验中,海温变化的空间分布受观测约束,故能将气候系统内部变率对于模式和观测之间差异的影响最小化。
卫星微波探测仪能够提供1978 年末至今的全球大气温度估计值(Mears and Wentz, 2017)。通过对原始资料进行反演得到的数据提供了相对于传统器测资料独立的全球对流层增暖的观测证据,由于该资料具有全球空间覆盖率高和数据质量均匀的特点,目前已被作为重要的大气观测资料广泛地应用于气温趋势的研究(Johanson and Fu, 2006;Santer et al., 2008; Po-Chedley et al., 2015; Mears and Wentz, 2016; Steiner et al., 2020)。然而,由于卫星资料的质量受均一化和后处理过程的影响,当前微波探测卫星产品的气温趋势放大率小于气候模式模拟值,也弱于根据湿绝热递减率计算所得的理论值(Santer et al., 2005, 2017b)。得益于对卫星轨道漂移订正与星载仪器校准方法的改进,近年来,卫星探测估算的大气温度资料质量得到了明显提升(Mears and Wentz, 2016; Zou et al., 2018)。
除卫星观测资料以外,覆盖时间较长的再分析资料也是研究大气温度变化的重要数据源。按照对观测资料和数值预报模式的依赖程度,再分析资料的输出变量通常可分为三类,其中大气温度属于第一类,主要受到同化的观测资料影响,可视为“真实情况”(Kalnay et al., 1996)。因此,再分析资料已被用于研究大气温度变化趋势,作为检验模式结果的“观测”证据。
FGOALS-g 是中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室(LASG/IAP)发展的气候系统模式,该模式参加了CMIP3、CMIP5 以及进行中的CMIP6,被广泛应用于各类气候变率和气候变化的研究(周天军等, 2014, 2020)。其中,参加CMIP5 的版本为FGOALS-g2,参加CMIP6 的最新版本为FGOALSg3。从FGOALS-g2 到FGOALS-g3,该模式从大气分量到海洋分量都得到诸多改进(Li et al.,2020b)。然而,目前尚不清楚FGOALS-g3 能否合理再现全球大气温度的变化趋势以及热带对流层放大现象。
本文基于国际上最新的卫星和再分析资料,以及FGOALS-g 新旧版本历史模拟试验和新版本AMIP 试验(GAMIL3)的模拟结果,拟重点回答以下关键科学问题:(1)FGOALS-g3 能否合理再现全球大气温度的变化趋势和热带对流层放大现象?若存在偏差,则模拟偏差产生的原因是什么?(2)FGOALS-g 新版本较旧版本性能是否有提升?若有提升,主要表现在哪些方面?(3)海气耦合过程(气候系统内部变率)对模拟结果有何影响?
2 模式、资料和方法
2.1 模式简介
FGOALS-g 是由LASG/IAP 发展的耦合气候系统模式,包含了大气、海洋、陆面和海冰四个模块。本文分析的两个版本分别是FGOALS-g2 和FGOALSg3,二者间的差异一是在大气模式,具体如表1 所示(Li et al., 2020a)。二是在海洋模式,FGOALSg3 的海洋模式分量为LICOM3,相对于LICOM2的改进主要包括两个方面:(1)动力框架由原来的经纬度格点框架改为适用于任意正交曲面坐标并采用了三极格点,有效解决了北极点引起的一系列计算稳定性问题;(2)改进了潮汐混合以及涡旋混合的物理过程(Lin et al., 2016, 2020)。FGOALSg3 的陆面分量为CAS-LSM(Xie et al., 2020),海冰分量为Los Alamos sea ice model Version 4.0。FGOALS-g3 采用NCAR 开发的CPL7 进行耦合。有关FGOALS-g3 相较于FGOALS-g2 模式改进的详细介绍和整体性能评估详见Li et al.(2020a)。

表1 GAMIL2 和GAMIL3 模式的主要差异Table 1 Main difference points between GAMIL2 model and GAMIL3 model
本文使用到的模式数据为FGOALS-g3 的历史模拟试验和单独大气模式GAMIL3 的AMIP 试验结果。其中,按照CMIP6 的标准设定,历史模拟试验使用历史外强迫(包括温室气体、气溶胶等)驱动耦合模式,模拟1850~2015 年的历史气候,给定初始场后海洋和大气自由耦合;单独大气模式试验利用1979~2015 年的观测海温和海冰作为边界条件,驱动大气模式GAMIL3,即AMIP 试验(周天军等, 2019)。为比较FGOALS-g 耦合模式新旧版本的差异,本文还使用了FGOALS-g2 历史模拟试验数据。上述每组试验均选取第一个集合成员,研究时段为1979~2015 年。
由于FGOALS-g2 的历史模拟试验截止于2005 年12 月,而典型浓度路径情景RCP8.5(Representative Concentration Pathways,RCP)未来预估试验是以历史模拟试验的终止年作为起始场进行模拟的,为便于比较,本文将FGOALS-g2 的历史模拟试验数据和RCP8.5 数据进行拼接,得到1850~2015 年的历史模拟数据。为方便讨论,以下分别用FGOALS-g2,FGOALS-g3 和GAMIL3来表示两个耦合模式的历史模拟试验和单独大气试验。
2.2 观测及再分析资料
本文用到的观测和再分析资料如下:
(1)MSU/AMSU 卫星温度资料。1978 年末以来,美国国家海洋和大气管理局(NOAA)的极轨卫星开始使用微波大气探测仪(Microwave Sounding Unit,MSU)和升级版的微波大气探测仪(Advanced Microwave Sounding Unit,AMSU)对氧分子的微波辐射进行测量(Mears and Wentz,2017; Zou et al., 2018)。MSU/AMSU 通过在不同微波频率下进行测量,得到不同高度层的微波辐射信息,进一步处理得到不同高度层的温度反演信息。本文使用的是美国加利福尼亚州的遥感系统公司(Remote Sensing Systems)提供的MSU/AMSU 卫星微波资料v4.0 版本(以下统称RSS4.0)。该数据集提供了分层逐月温度资料,覆盖时间段为1979 年至今,水平分辨率为2.5°×2.5(Mears and Wentz, 2016)。本文用到的变量为平流层低层温度(TLS)、对流层中高层温度(TMT)和对流层低层温度(TLT)。其权重函数峰值对应高度(气压)分别为17 km(75 hPa)、5 km(540 hPa)和2 km(795 hPa),与平流层低层、对流层中高层和对流层低层的典型高度相对应(Steiner et al.,2020)。
(2)欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMRWF)新一代再分析资料ERA5(Hersbach et al., 2020)。用到的变量为逐月的气温、地表温度、表面气压、海陆分布和海冰范围,覆盖时间段为1979 年至今,水平分辨率为1°×1°,气温垂直高度有37 层。本文使用的ERA5.1 气温数据订正了原ERA5 数据在2000~2006 年期间的冷偏差,平流层和对流层上层温度更为可靠(Simmons et al., 2020)。
基于不同资料的覆盖时段,本文的分析时段统一为1979~2015 年。
2.3 分析方法
2.3.1 合成卫星温度计算方法
为方便将模式结果与卫星数据进行比较,本文使用了RSS 开发的局地权重函数法,分别将模式输出数据和ERA5.1 再分析数据转换为合成卫星温度(Santer et al., 2017b)。该方法在每个经纬网格点上将模式和再分析数据的温度廓线同局地权重函数进行卷积。权重取决于该格点的表面气压、下垫面类型(陆地、海洋或海冰)以及选取的层平均温度(TLS、TMT 或TLT)。该方法较全球平均权重函数法能够提供更为准确的合成卫星温度,其在高海拔地区准确度的提升效果尤为明显(Santer et al., 2017a)。
2.3.2 TMT 订正方法
星载微波探测仪反演的TMT 变化趋势受到平流层低层降温的显著影响(Fu and Johanson, 2004,2005; Johanson and Fu, 2006)。平流层降温对TMT的大部分影响可以通过回归技术去除(Fu et al., 2004)。该方法的可靠性在观测和模式气温数据中都得到了验证(Fu and Johanson, 2004; Gillett et al., 2004)。参考Fu and Johanson(2005),本文采用这一订正方法,具体如下:
其中,a24的选取参考Santer et al.(2017a),在所有纬度均为1.1。
2.3.3 理论廓线计算方法
为得到气温变化趋势随高度变化的理论结果,利用1979~2015 年的ERA5.1 再分析数据,基于1000 hPa 温度和80%相对湿度分别作为初始条件,计算得到两条湿绝热线,做差即可得到气温垂直廓线的理论值(Santer et al., 2005; Steiner et al.,2020)。所用公式如下:
其中,k=0.286,T为气温,p为 气压,L为蒸发潜热,cp为 定压比热,ws为饱和混合比。
2.3.4 滑动线性趋势计算方法
不同分析时段的选取会对温度变化趋势的估算产生影响,为了减小线性趋势对于分析时段的依赖性,本文参考Santer et al.(2011, 2017b)提出的最大重叠L-年趋势计算方法,选取L=10 和L=20 两个时段进行分析。这种方法可以有效去除季节尺度和年际尺度“噪音”对于温度趋势的影响,从而突出温度变化在年代际时间尺度上的基本特征。
以L=10 为例,用于计算第一个10 年线性趋势的时段为1979 年1 月至1988 年12 月,随后起止月份逐次后移1 个月,最后一次计算时段为2006 年1 月至2015 年12 月。
2.3.5 显著性检验方法
本文使用非参数Thei-Sen 趋势估计法(Ohlson and Kim, 2015)计算线性趋势,线性趋势的显著性检验使用了非参数Mann-Kendall(MK)检验方法。
本文所涉及的空间相关系数、时间相关系数等相关分析均使用了双侧Studentt检验,自由度为样本数减2。
3 结果分析
本文首先针对不同高度上全球平均温度的长期变化,通过模式与观测和再分析的比较来评估模式性能。随后,分析对流层中高层与下层温度序列的回归系数空间分布,将研究区域聚焦于热带(海洋),重点关注该地区增温趋势随高度升高而增大的现象。对于该现象,本文选取4 个指标来检验模式的性能并分析内部变率对结果的影响,包括对流层高低层温度回归场的空间相关系数、放大系数(高低层平均温度的回归系数)的年代际尺度变化、对流层高低层平均温度序列的长期趋势和年际变率、热带平均温度的垂直廓线。
3.1 全球温度变化趋势
图1 给出了1979~2015 年不同高度层(TLS、TMT 和TLT)全球平均温度随时间演变情况。观测中平流层低层呈降温趋势(图1a),主要由人类活动引起的平流层臭氧消耗造成,大气CO2浓度升高也有一定贡献(Aquila et al., 2016; Maycock et al., 2018)。平流层低层的降温趋势有两次突变,分别与1982 年El Chichón 和1991 年Pinatubo 火山爆发引起的强增暖信号有关。火山爆发使得大量硫酸盐气溶胶进入平流层,通过吸收近红外和长波辐射导致平流层增温(Robock, 2000)。
FGOALS-g3 和GAMIL3 均能再现平流层低层的长期变冷趋势以及火山爆发引起的两次增温,但都低估了El Chichón 火山爆发造成的平流层增暖,同时高估了Pinatubo 火山的影响,原因是驱动模式的平流层火山气溶胶强迫资料对于两次火山爆发强度的估计不够准确(Rieger et al., 2020)。FGOALSg2 由于未考虑火山气溶胶强迫(Zhou and Song,2014),故无法再现平流层低层的突变增暖信号,FGOALS-g3 较FGOALS-g2 增加了对于平流层火山气溶胶强迫的响应。
图1b 和c 分别为1979~2015 年全球平均TMT和TLT 距平序列。在观测中,对流层(上下两层)在1979~2015 年间主要表现出较为一致的增暖特征。

图1 1979~2015 年全球平均温度距平序列(单位:°C):(a)平流层低层(TLS);(b)对流层中高层(TMT);(c)对流层低层(TLT)Fig.1 Global mean temperature anomalies series (units: °C) from 1979 to 2015: (a) Lower stratosphere temperature; (b) mid-to-upper troposphere temperature; (c) lower troposphere temperature
定量比较结果表明(表2),观测和模式一致表现为平流层低层降温、对流层增温。具体而言,卫星资料和再分析资料揭示的对流层中高层增温幅度分别为0.17°C (10 a)-1、0.12°C (10 a)-1,对流层 低 层 增 温 幅 度 分 别 为0.20°C (10 a)-1、0.14°C(10 a)-1。FGOALS-g2 和FGOALS-g3 均 可 再 现 观测中的对流层显著增暖趋势,但均高估了观测的增温趋势值,原因与气候系统内部变率有关。前人研究表明若历史模拟试验与观测的内部变率位相相似,则模拟的对流层增温趋势与观测更为接近(Po-Chedley et al., 2021)。注意FGOALS-g3 较FGOALSg2 表现出更强的增温趋势,这与二者模拟的内部变率位相不同以及驱动模式的历史模拟外强迫存在差异有关。GAMIL3 的AMIP 试验由于受历史观测海温驱动,其内部变率位相与观测一致,故模拟的对流层增温幅度与卫星观测结果基本一致。

表2 5 套数据1979~2015 年全球平均平流层低层(TLS)、对流层中高层(TMT)和对流层低层(TLT)线性趋势 [单位:°C (10 a)-1],所有趋势均通过99%的信度水平检验Table 2 Linear trend of the global averages of Temperature of Lower Stratosphere (TLS), Temperature of Mid-to-upper Troposphere (TMT), and Temperature of Lower Troposphere (TLT) from 1979 to 2015 [units: °C (10 a)-1], all the linear trends are significant at the 99% confidence level
不同分析时段的选取会对温度变化趋势的估算产生影响,为减小线性趋势对于分析时段的依赖性,参考Santer et al.(2011, 2017b)的方法,图2 比较了模式和观测中不同高度层温度的滑动线性趋势。在观测中,平流层低层温度的10 年滑动趋势主要反映了平流层低层温度对El Chichón 和Pinatubo 火山爆发的响应(图2a),其最大增温趋势出现在El Chichón 火山爆发造成的小幅增暖时期结束与Pinatubo 火山爆发造成的大幅增暖时期之间,最大降温趋势值出现在Pinatubo 火山造成的平流层低层增暖峰值期之后。FGOALS-g3 的结果与观测较为一致,而FGOALS-g2 由于未包含火山气溶胶辐射强迫模块故与观测结果差距较大。GAMIL3 与FGOALS-g3 结果相近,均能够合理再现观测特征。图2b 中平流层低层温度20 年滑动趋势则主要反映的是气温在平流层臭氧消耗期和臭氧恢复期的年代际变化。
在观测资料中,对流层上下两层的温度变化趋势较为一致(图2c-f)。当滑动时长取10 年时,观测数据表现出双峰结构特征(图2c,e)。双峰结构是由火山爆发后的温度恢复和人为活动造成的全球变暖共同引起的。观测资料受厄尔尼诺—南方涛动(ENSO)等年际变率的掩盖,双峰结构不如模拟明显(Santer et al., 2014)。在两个耦合模式(FGOALS-g2 和FGOALS-g3)的结果中,双峰结构较观测更为明显。GAMIL3 的结果与观测一致,双峰结构不明显,原因是受到年际变率的影响。对于20 年滑动趋势,FGOALS-g3 模拟的增温速率在1990s 显著高于观测值,主要是由于受到了驱动模式的外强迫系统性偏差(Li et al., 2020b)以及气候系统内部变率(Po-Chedley et al., 2021)的影响。
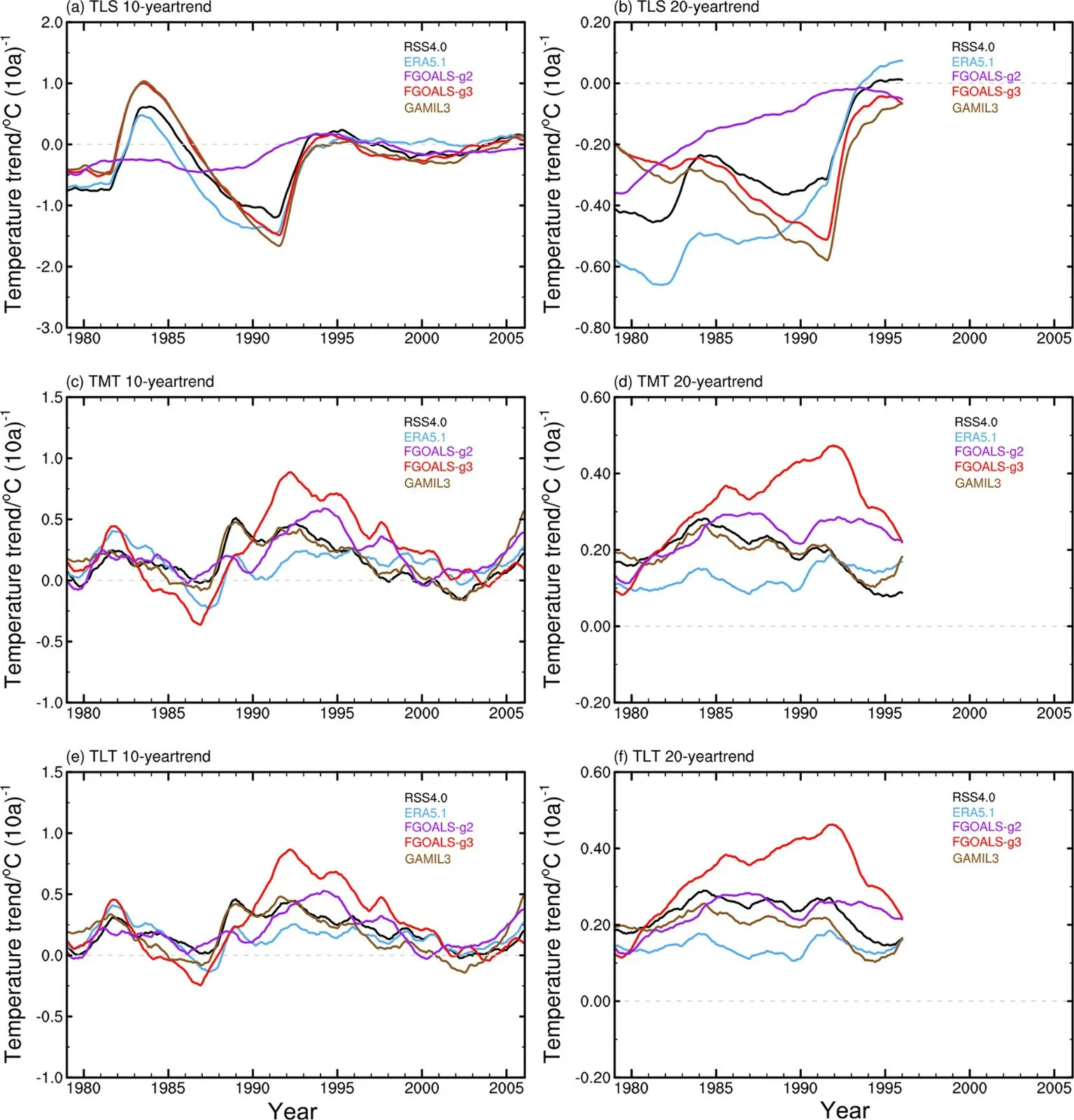
图2 全球平均气温10 年(左列)和20 年(右列)滑动趋势 [单位:°C (10 a)-1]:(a,b)平流层低层;(c,d)对流层中高层;(e,f)对流层低层。横坐标为起始时间Fig.2 10 years’ (left) and 20 years’ (right) sliding trend of the global mean temperature [units: °C (10 a)-1]: (a, b) Lower stratosphere; (c, d) midto-upper troposphere; (e, f) lower troposphere.The abscissa is the starting time
图3a-f 给出了RSS4.0 卫星、ERA5.1 再分析和GAMIL3 单独大气模式试验中对流层中高层及对流层低层温度趋势的全球空间分布。三套数据所揭示的对流层温度趋势的空间分布型较为一致,增暖趋势大值区均位于北半球中高纬,以及西南太平洋等地区。定量估算对流层中高层和低层全球平均温度的趋势,RSS4.0 卫星数据的结果分别为0.15°C(10 a)-1和0.19°C (10 a)-1,ERA5.1 再分析数据结果为0.12°C (10 a)-1和0.13°C (10 a)-1,GAMIL3 的结果均为0.18°C (10 a)-1。因此,GAMIL3 与RSS4.0卫星数据的结果一致,而ERA5.1 再分析数据所揭示的全球平均增温趋势相对较小。三套数据各自的对流层中高层和对流层低层温度变化趋势的空间分布也较为一致,反映在空间相关系数上,RSS4.0、ERA5.1 和GAMIL3 的 结 果 分 别 为0.75、0.88 和0.90(均通过99%的信度水平)。
对于全球平均而言,对流层上下层温度变化趋势比较接近。其中利用RSS4.0 卫星和ERA5.1 再分析数据估算的全球平均对流层上下层温度变化趋势之比分别为0.82 和0.91,GAMIL3 的结果为1.0,三套数据的结果均不大于1。温度变化趋势因纬度而异,在高纬地区,对流层中高层温度增暖趋势弱于低层,而在低纬地区,对流层中高层温度的增暖趋势则强于低层,呈现出“热带对流层放大”现象。
图3g-j 给出了FGOALS-g2 和FGOALS-g3 历史模拟试验的对流层中高层及对流层低层温度变化趋势的全球空间分布。FGOALS-g2 和FGOALSg3 模拟的空间分布型存在一定差异,可能与CMIP6和CMIP5 采用的历史模拟外强迫资料差异有关。相较于CMIP5,CMIP6 历史模拟外强迫的气溶胶冷却效应减弱并增加了温室气体的空间分布,外强迫资料的差异会引起增温趋势空间分布的差异(Nie et al., 2019; Li et al., 2020b)。
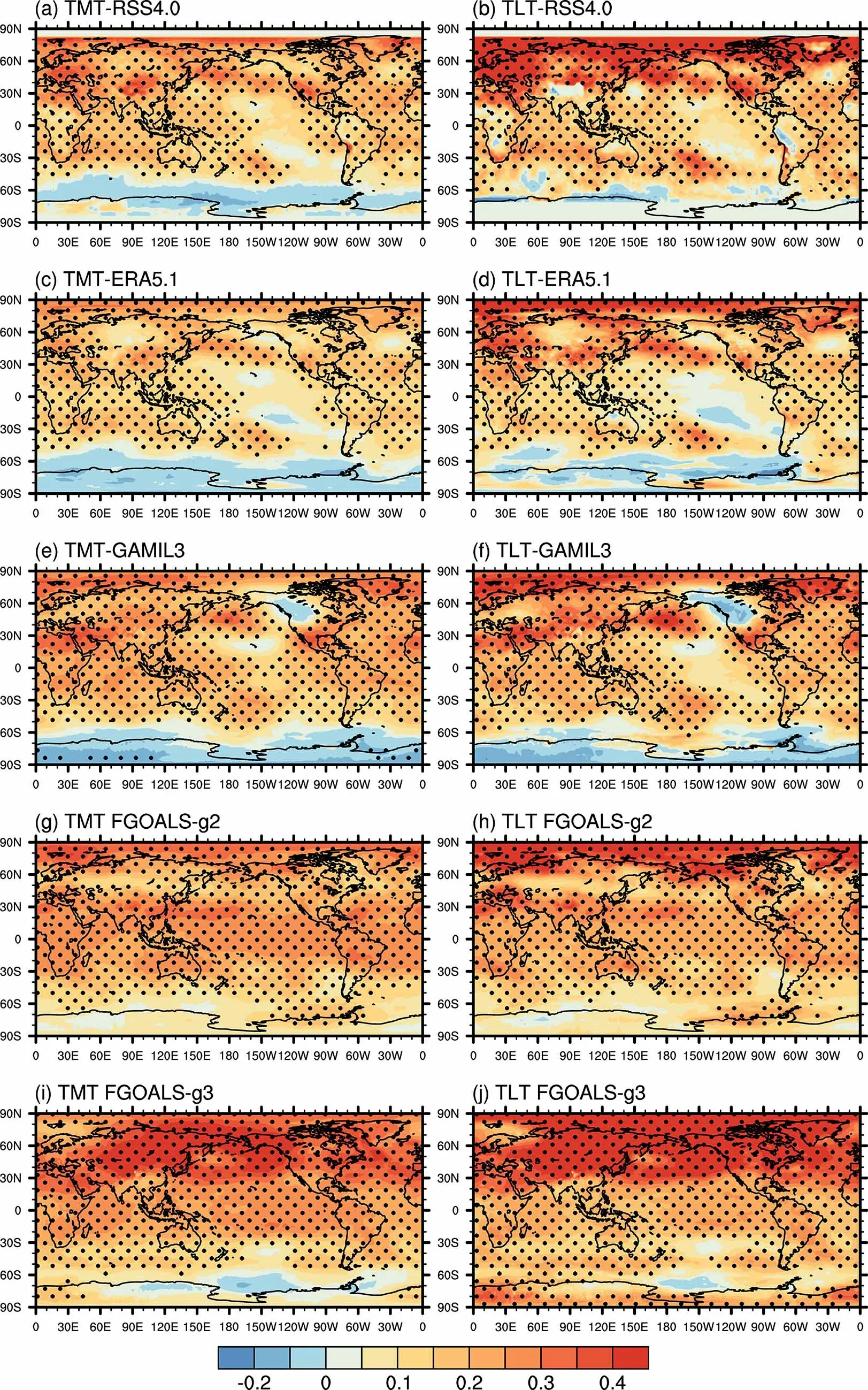
图3 1979~2015 年对流层中高层(左列)和对流层低层(右列)气温变化趋势 [单位:°C (10 a)-1]:(a,b)RSS4.0 卫星资料;(c,d)ERA5.1 再分析资料;(e,f)GAMIL3;(g,h)FGOALS-g2;(i,j)FGOALS-g3。打点区域表示通过95%的信度水平检验Fig.3 Temperature variation trends in the mid-to-upper troposphere (left) and lower troposphere (right) in 1979-2015 [units: °C (10 a)-1]: (a,b) RSS4.0; (c, d) ERA5.1; (e, f) GAMIL3; (g, h) FGOALS-g2; (i, j) FGOALS-g3.The dotted area indicates the significant values at the 95%confidence level
就对流层中高层和低层全球平均温度变化趋势而 言,FGOALS-g2 的 结 果 为0.22°C (10 a)-1和0.21°C (10 a)-1,FGOALS-g3 的结果为0.25°C (10 a)-1和0.26°C (10 a)-1。两个版本的耦合模式模拟结果均明显高于观测和GAMIL3 的结果。
关于全球平均对流层上下层温度变化趋势之比,FGOALS-g2 和FGOALS-g3 的结果分别为1.04 和0.96,与GAMIL3 的结果基本一致。此外,针对高纬地区对流层中高层增温趋势小于低层、低纬地区对流层中高层增温趋势大于低层这一特征,两个耦合模式的结果与观测相符。
3.2 热带对流层放大
为直观描述高低纬地区在对流层上下层增温特征上的不同,图4 给出了对流层中高层温度与低层温度回归系数的空间分布。观测和模拟结果在热带地区(20°N~20°S)的回归系数均大于1,一致表现出对流层中高层温度变化相对于对流层低层放大的现象,且空间分布型表现较为稳健,大值区均出现在赤道辐合带和南太平洋辐合带等典型的热带海洋深对流旺盛区。
如图4a 所示,RSS4.0 卫星数据揭示的西太平洋暖池区的热带对流层放大的强度明显低于另外4套数据,其特征也与湿绝热递减率理论不符。据前人研究,这种现象可能是由于卫星资料自身的残余非均匀误差造成的(Mears and Wentz, 2016)。以ERA5.1 资 料 为 基 准,FGOALS-g3、GAMIL3 和FGOALS-g2 与其在热带地区(20°N~20°S)的空间相关系数分别为0.79、0.80 和0.72(均通过99%的信度水平)。这表明FGOALS-g3 与GAMIL3 均能较好地模拟出热带对流层放大现象的空间分布,FGOALS-g3 较FGOALS-g2 对热带对流层放大现象的模拟能力有明显提升。
热带对流层放大现象有其理论基础。热带地区深对流活动旺盛,基于湿绝热递减率理论,热带深对流旺盛海区的气块湿绝热上升会放大地表增暖,在约200 hPa 高度上产生增暖峰值,从而呈现出对流层放大的特征(Stone and Carlson, 1979; Hegerl and Wallace, 2002)。下面我们将着重关注热带区域。
图5a、b 给出了RSS4.0 卫星、ERA5.1 再分析和GAMIL3 单独大气模式试验在热带地区(20°N~20°S)对流层中高层及低层温度的距平序列。在观测中,热带地区对流层(高低两层)在1979~2015 年间主要表现出较为一致的增暖趋势,同时叠加有年际尺度的波动。GAMIL3 模式的AMIP 试验由于受历史观测海温驱动,其内部变率位相与观测一致,故模拟的热带地区对流层增温幅度和年际尺度波动与观测结果基本一致,反映在时间相关系数上,GAMIL3 与RSS4.0 和ERA5.1 在对流层中高层的结果分别为0.83 和0.81,在对流层低层为0.86 和0.83(均通过99%的信度水平)。
图5c、d 给出了FGOALS-g2 和FGOALS-g3历史模拟试验模拟的热带地区对流层上下层温度距平序列。FGOALS-g2 和FGOALS-g3 均可再现观测中的升温趋势,但年际尺度波动与观测结果差别较大,这种差异主要源于就内部变率的位相而言耦合模式与实际观测不是严格对应的。

图5 热带地区(a,c)对流层中高层和(b,d)对流层低层温度距平序列(单位:°C):(a,b)RSS4.0、ERA5.1 和GAMIL3 试验;(c,d)FGOALS-g2 和FGOALS-g3 历史模拟试验Fig.5 Temperature anomalies series in the (a, c) mid-to-upper troposphere and (b, d) lower troposphere over the tropics (units: °C): (a,b) RSS4.0, ERA5.1, and GAMIL3; (c, d) FGOALS-g2 and FGOALSg3
定量比较结果表明(图6),卫星资料和再分析资料揭示的热带地区对流层中高层增温幅度分别为0.15°C (10 a)-1和0.12°C (10 a)-1,对流层低层增温 幅 度 分 别 为0.14°C (10 a)-1和0.10°C (10 a)-1。GAMIL3 在对流层中高层的增温幅度为0.22°C(10 a)-1,对流层低层为0.18°C (10 a)-1,FGOALSg3 和FGOALS-g2 在对流层中高层均为0.26°C(10 a)-1,低层均为0.22°C (10 a)-1。模式结果均可再现观测中的热带地区对流层显著增暖趋势,但均高估了观测的增温趋势值。
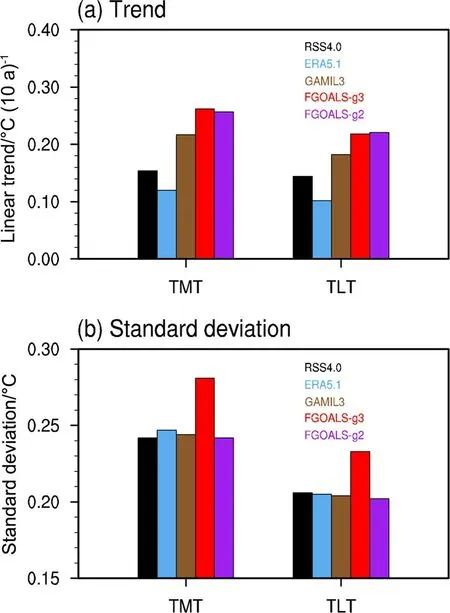
图6 (a)1979~2015 年热带地区(20°N~20°S)平均对流层中高层和对流层低层温度距平序列的最小二乘线性趋势 [单位:°C(10 a)-1],所有趋势均通过99%的信度水平。(b)同(a),但为标准差(单位:°C)Fig.6 (a) Least-squares linear trend of mean temperature anomalies in the mid-to-upper and lower troposphere over the tropical region(20°N-20°S) from 1979 to 2015 [units: °C (10 a)-1]; all the linear trends are significant at the 99% confidence level.(b) Same as (a), except for the standard deviation (units: °C)
就对流层上下层热带平均温度的年际变率而言,观测和模式模拟的对流层中高层结果均大于对流层低层,说明热带对流层放大现象不仅表现在长期趋势上,在年际变率上同样有体现。此外,FGOALSg3 在对流层上下层的温度序列标准差分别为0.28和0.23,明显高于观测、GAMIL3 和FGOALS-g2的结果。
为揭示观测和模式在对热带对流层放大现象的刻画方面产生差异的原因,本文参考Fu et al.(2011)提出的方法,采用公式TMT-TLT=c×TLT(TMT 和TLT 分别表示对流层中高层和低层温度序列的趋势或标准差)表征热带对流层放大的幅度。模式与观测之间的差异由2 个因素决定:对流层低层自身的温度变化(TLT)和增幅因子c。
就温度变化趋势而言,卫星和再分析资料揭示的增幅因子c分别为0.07 和0.18,GAMIL3、FGOALS-g3 和FGOALS-g2 的结果分别为0.19、0.20 和0.16。模式模拟的对流层低层温度趋势和增幅因子均大于卫星资料的结果,造成了模式与卫星观测之间的差异。模式与再分析资料之间差异的主要原因是ERA5.1 数据中对流层增温趋势偏弱。就温度年际变率而言,卫星和再分析资料揭示的增幅因子c分别为0.20 和0.17,GAMIL3、FGOALSg3 和FGOALS-g2 的结果分别为0.20、0.21 和0.20。FGOALS-g3 与观测结果之间差异的主要原因是模式模拟的对流层低层温度年际变率偏强。
由于分析时段会影响热带对流层放大的特征(Santer et al., 2017b),为考察热带对流层放大的时段依赖性,本文将对流层中高层与低层温度序列的回归系数在热带海区的平均值定义为“放大系数”b。此处的放大系数b和前文采用的增幅因子c均为衡量对流层中高层与对流层低层温度变化相对大小的指标,二者所使用的计算方法不同,含义也有所区别:放大系数b为回归系数,表征对流层中高层与对流层低层温度序列自身变化的相对大小;增幅因子c为比值,表征对流层中高层温度变化幅度(趋势或标准差)较对流层低层放大的倍数。
图7 给出了放大系数b随分析时段的变化情况。卫星资料的b值较再分析资料明显偏小,这与其在西太平洋暖池区的表现有关(图4a),据前人研究,这可能是其自身残余误差造成的(Po-Chedley et al., 2015)。此外,卫星资料的结果在时间尺度超过15 年时出现减小趋势,考虑其对不同微波探测仪信息融合方案的高度敏感,我们推测融合方案中含有影响其多年代际表现的残余非均匀误差。ERA5.1 再分析资料的结果始终稳定在1.22 附近。
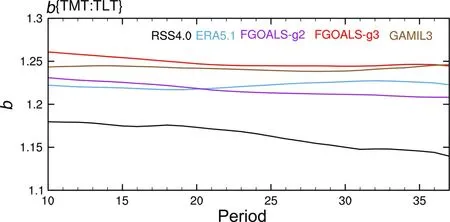
图7 5 套数据的热带海洋平均放大系数(b)随选取时段的变化情况。横坐标为选取时段长度(10 年至37 年)Fig.7 Variation of the mean amplification factor (b) of the tropical oceans with the selected period, and the abscissa is the selected period length (10 years to 37 years)
模拟和再分析数据的放大系数b均大于1,表明热带海区对流层增温趋势随高度增加而增大,且均不随选取时段的长短发生变化,这符合理论和基本的物理定律(Stone and Carlson, 1979; Santer et al., 2005)。FGOALS-g2 与ERA5.1 的结果在数值上基本一致,而FGOALS-g3 和GAMIL3 的结果均大于再分析资料。
需要指出的是,卫星资料无法显示温度廓线,而再分析资料揭示的廓线也因为同化了无线电探空仪数据而存在结构性偏差(Hersbach et al., 2020),因此模式模拟的温度廓线与再分析数据结果有差异并不一定就意味着模式有偏差。参考Santer et al.(2005)和Steiner et al.(2020),本文引入了根据湿绝热递减率计算的理论结果。图8a 给出了ERA5.1 再分析、GAMIL3、FGOALS-g3、FGOALSg2 中不同高度层的温度变化趋势与1000 hPa 对应值之比的廓线及理论结果。ERA5.1 再分析结果与理论值差异较大,这与其同化的无线电探空资料有关。前人基于无线电探空资料的分析与本文基于再分析数据的结果基本一致(Santer et al., 2008;Hersbach et al., 2020)。FGOALS-g3 和FGOALS-g2的结果均与理论值较为一致,表明两代耦合模式对于放大率廓线的模拟能力较高。GAMIL3 单独大气试验的结果明显异于理论廓线,除1000 hPa 外,其各层比值均明显大于理论结果。
为揭示GAMIL3 放大率廓线异于理论结果的原因,图8b 给出了热带地区平均的各层温度变化趋势廓线。GAMIL3 模拟的各层增温趋势值较理论值均偏弱,但在925 hPa 以上与再分析资料较为一致。这种长期趋势的整体偏弱体现了海气耦合过程对于模拟结果的直接影响:对流层温度的长期变化趋势主要受到外强迫变化(温室气体增加等)的影响,而GAMIL3 单独大气模式由于受到观测海温驱动,故无法通过海气耦合过程体现出外强迫变化对于对流层增温趋势的作用,从而使得模拟结果出现负偏差。此外,1000 hPa 增温趋势明显偏弱是GAMIL3 放大率廓线明显异于理论结果的主要原因。
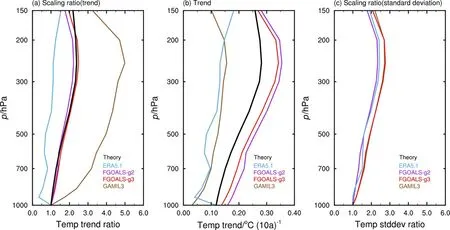
图8 (a)1979~2015 年热带地区(20°N~20°S)平均各层温度趋势与1000 hPa 温度趋势之比(单位:1),黑线为根据假绝热过程计算的理论值。(b)同图(a),但为温度趋势 [单位:°C (10 a)-1]。(c)同图(a),但为温度的年际变率之比)Fig.8 (a) Ratio of the average temperature trend of each layer in the tropical region (20°N-20°S) to the temperature trend of 1000 hPa in 1979-2015(units: 1).The black line is the theoretical value calculated according to the pseudo-adiabatic process.(b) The same as figure (a), except for the temperature trend [units: °C (10 a)-1].(c) Same as fig.(a), except for the ratio of interannual variability
由于AMIP 型海温驱动试验在设计上主要适用于分析年际变率,而热带对流层放大现象在年际尺度上同样存在(图6b),故推测GAMIL3 在对流层温度年际变率上的表现应更为合理。图8c 给出了再分析资料和模式模拟的年际变率放大率廓线,GAMIL3 与再分析资料和耦合模式非常接近,这印证了上述推测。
4 结论
热带对流层放大现象是气候变化的显著特征,也是检验气候模式性能的重要指标。FGOALS-g3是中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室(LASG/IAP)发展的最新版本气候系统模式。本文基于RSS4.0 卫星资料和ERA5.1 再分析资料,系统分析了FGOALSg3 对全球大气温度变化和热带对流层放大的模拟能力及偏差产生原因;并通过新旧版本(FGOALSg3 与FGOALS-g2)的比较揭示了新版本模式技巧的提升;通过比较FGOALS-g3 历史模拟试验与GAMIL3 单独大气试验结果,揭示了海气耦合过程对模拟结果的影响。主要结论归纳如下:
(1)在全球大气温度变化方面,FGOALS-g3能够合理再现观测中的全球对流层显著增温趋势,但其模拟的增温趋势偏强,这与气候系统内部变率以及两代气候系统模式所使用的历史气候外强迫资料存在差异有关。在热带对流层放大方面,FGOALSg3 能够合理再现观测中的空间分布模态、放大系数的年代际尺度变化以及热带平均温度的垂直廓线,偏差产生的主要原因是其模拟的对流层低层温度变化偏强。
(2)FGOALS-g3 较FGOALS-g2 在性能上有一定提升,主要表现为:由于增加了火山气溶胶强迫,使得其在对于平流层火山气溶胶强迫的响应方面实现了从无到有的跨越;模拟的热带对流层放大现象的空间分布更加接近观测;模拟的热带地区平均气温趋势的垂直廓线更加接近基于湿绝热递减率理论的结果。
(3)耦合模式和单独大气模式结果间的差异主要表现为两个方面,一是GAMIL3 模拟的气温趋势值较FGOALS-g3 更接近于观测结果,其气温时间序列及空间分布与观测值的相关系数也更高,原因在于AMIP 型试验中海温变化的空间分布给定了观测值,能够合理反应实际的年际变率;二是GAMIL3 较FGOALS-g3 在热带地区温度长期趋势方面存在结构性偏差,而在年际变率方面表现合理,原因是GAMIL3 的AMIP 试验缺少海气耦合过程,无法合理反映海洋在对流层增温中的反馈作用。

