基于XGBoost算法的盾构施工地面沉降预测方法

夏汉庸,黄 毅,尹和军,张 良

(1.宁波市轨道交通集团有限公司,宁波 315012；2.中铁工程设计咨询集团有限公司,北京 100055)

1 概述

盾构法隧道施工会对地层原有的应力平衡造成较大影响，因此，掌握施工对邻近地面的影响，及时准确、智能地预测地面沉降量，为盾构掘进风险管控提供有效的依据，具有重大的工程价值。目前，盾构施工主要采用传统地面沉降监控量测方法，但监测数据的采集频率相对较低且反馈不及时，不能及时掌握盾构经过地面的详细沉降情况，出现问题均为事后采取控制，因此，通过跨学科融合研究进行数据分析来预测地面沉降量显得尤为重要。

盾构施工过程中地面沉降预测常用的传统方法有数值模拟法和Peck公式法。Peck公式[1]是在隧道工程中影响较为广泛的预测地面沉降方法，后续在此方面的深入研究得到了广泛开展[2-5]，但采用经验公式计算时，因关键参数与经验因素过于依赖特定经验，局限性比较大；而采用数值模拟计算时计算量又较大，建模效率过低且参数选取过于复杂。

近几年，利用人工智能方法对盾构施工过程中地面沉降量的预测成为主流。众多研究者利用人工神经网络模式[6]、BP神经网络训练模型[7]、小波理论[8]、时序分析[9]、自适应神经模糊推理系统(ANFIS)[10-13]等研究理论深入研究了盾构施工地面沉降问题，构建了各种有效的预测模型。此外，支持向量机在地面沉降预测研究中也得到了广泛使用[14-18]，在解决小样本和高维模式识别问题中具有巨大优势，且其在解决非线性回归问题上也具有良好的性能。综上所述，人工智能方法已被广泛应用到地面沉降预测中，实现了对地质参数和掘进参数的筛选，构建了具有较高准确率的地面沉降预测模型，并在模型优化方面做了研究。基于上述筛选后的参数数据建立了精度较高的预测模型，并对模型的参数调优进行了大量研究。但当前多数对地面沉降预测的研究局限于单点单模型预测，针对施工过程中盾构掘进多点产生的地面沉降同步预测研究较少[19]。

以数据融合分析为出发点，通过数据挖掘技术构建预测模型，利用挖掘参数等与沉降相关联的数据作为输入数据，而盾构多监测点的沉降量作为输出数据，以此构建单一地层地面沉降预测模型，最终实现盾构过程中多点同步预测，同时具备建模简单、准确率高等优点。

2 地面沉降预测方法研究

盾构施工中地面沉降监测点布置分为以下两种：①纵向沉降监测点，一般每隔3～5 m布置于隧道轴线的正上方；②横向沉降监测点，以纵向监测点为中心对称布置，一般范围为20 m，左右两侧各设4个点，并且与中心点的距离分别为2，4，6，8 m。根据上述监测点的布置方案，将开挖面后20环至前20环作为纵向沉降预测范围，并且横向沉降预测范围为上述纵向范围中各横断面的所有监测点。横断面内的测点布置示意如图1所示。

图1 横断面监测点布置示意(单位：m)

横向地面沉降是指垂直于隧道周线平面内的地面沉降，横向地面沉降槽形状类似于正态分布曲线。研究表明，纵向地表沉降的发生持续时间较长，按照沉降发生的不同原因，纵向地表沉降过程大致分为先期沉降、盾构到达时的地面沉降、盾构机通过时地面沉降、盾尾间隙地面沉降和后期沉降5个阶段。本次研究对象为盾构掘进过程中因施工所产生的纵向地表沉降量。基于上述场景分析，地面沉降预测方法的实现步骤如图2所示。

图2 基于XGBoost的地面沉降量预测方法

(1)数据预处理。对数据库中的沉降量数据和掘进参数数据进行空值填充和去除异常值，最后再进行归一化处理，得到预处理后的沉降量数据和掘进参数数据。

(2)关键影响因素提取。在确定单一地层相关地质参数的情况下，利用基于随机森林的地面沉降影响分析因素模型对预处理后的盾构掘进各种参数进行筛选，得到地面沉降关键影响因素集、关键参数等。

(3)地面沉降预测。构建基于XGBoost的地面沉降预测模型，模型输入为上步中提取出的关键影响因素，对各个监测点进行沉降量预测。

如若预测评价效果不满足精度要求，首先，需考虑对模型参数进行优化后重新预测；若优化后效果仍不佳，需考虑影响因素选取问题，并通过随机森林算法重新选取影响因素，并对其进行重新预测；若上述方法仍不能达到精度要求，则须考虑数据包重构。

基于XGBoost的盾构施工地面沉降预测受施工过程中的风险监测和施工操作因素影响，需利用当前时刻的盾构掘进参数和地面沉降值，即为掘进参数与地面沉降量二者间典型的耦合关系求解问题。涉及到掘进参数与地面沉降关键影响因素，以及地面沉降关键影响因素与沉降量之间的关系求解，由此，设计了求解二者之间耦合关系的数学表达式

Sd=f(x1，x2，…，xn)

(1)

式中，S为沉降量；d为不同监测点；x1，x2，…，xn，表示与地面沉降相关的影响因素(涉及掘进参数)；f为地面沉降预测函数(拟采取XGBoost进行建模)。

2.1 数据预处理

针对盾构施工产生的数据特点，采用以下3种数据预处理方法。

(1)缺失值处理

原有数据集的某行或某列中存在缺失数据，即为缺失值，针对不同的数据缺失情况，需有不同的处理方法。当某行的缺失值数量超出设定的阈时，即缺失值较多时，较常用的处理方法为忽略该条记录；某列缺失值较多时处理方法也为忽略该属性。当缺失量较小时，通常会采用缺失值填充的方法，主要有手工填充、属性平均值填充、属性众数填充以及利用其他属性并采用回归拟合的填充方法，如：①利用总体数据均值填充的均值插补法；②利用缺失数据从第1到k近邻数据的均值进行填充的近邻插补法；③以某种概率对数据进行多次抽样，并用抽取数据单元值的均值进行填充的随机插补法。文中采用均值插补法对原数据的缺失值进行填充。

(2)异常值处理

在数据集中存在不合理的值即为异常值，又称为离群点。分箱(Binning)、聚类(Clustering)和回归(Regression)是较为常用的处理异常值方法。本文采用分箱法处理异常值。

分箱法是指将数据以不同的规则分到不同的箱子里(“箱子”即为数据区间)，则处于箱子之外的属性值即被当作异常值，分箱法如图3所示。

图3 箱线图示意

图3中，各符号含义如表1所示，其中，异常值为大于QU+1.5IQR，小于QL-1.5IQR的属性值。箱线图的符合含义如表1所示。

表1 箱线图符号

(3)数据的无量纲化

将不同区间的各属性数据按照一定比例进行缩放处理，转化到同一个区间。这一方法能够将数据转化为无量纲数据，消除数据单位的限制。该数据处理步骤对于涉及计算距离的模型极为重要，目前，min-max标准化(Min-max normalization)和z-score标准化(Zero-mean normalization)为较常用的无量纲方法。

①归一化(Min-max normalization)

min-max归一化是指对原始数据进行线性变化，使其映射到[0，1]之间，也被称为离差标准化，变换公式为

x*=(x-xmin)/(xmax-xmin)

(2)

式中，xmax为样本数据的最大值；xmin为样本数据的最小值。

②标准化(Zero-mean normalization)

z-score标准化是指依据原数据的均值与标准差对其进行标准化，处理后的数据符合均值为0，标准差为1的标准正态分布，其也被称为标准差标准化，变换公式为

(3)

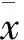
2.2 基于随机森林的地面沉降关键影响因素分析

影响地面沉降量的因素众多，筛选出关键影响因素，并对其进行更深层次的挖掘是进行地面沉降准确预测的重要前提。针对盾构施工数据体量大、种类繁多以及数据质量低的特点，需进行有效特征提取。近年来，随机森林算法大量应用于预测与分类、特征选取与异常值检测中，其能够较好地分析具有复杂相互作用的分类特征，学习速率较快，对于异常值与存在缺失值的数据鲁棒性能较好。同时，随机森林在回归问题中能够依据平均模型拟合误差选取特征集合[20-21]，因此，本文对涉及地面沉降预测的现有业务基础进行梳理，分析地面沉降变形机理及地表沉降变形规律。以不同地层下的掘进参数为主进行分析，将随机森林特征选择方法与机理分析相结合筛选相应地层下地面沉降关键影响因素，从而提高数据质量并保证预测的准确性，具体分析流程如图4所示。

图4 随机森林回归影响因素分析流程

第一步：回归树构建。

对应地层下的掘进参数作为原数据集，对这一数据集采取有放回随机抽样。通过给定N条训练数据集，每次抽取M条样本(M≤N)，随机抽取k次并构建棵回归树，每次未抽到的(N-M)条数据样本即为测试样本集，也被称为袋外测试数据ooB(out-of-Bag)。在总特征数为d的情况下，每次随机抽取f个(f≤d)。k棵回归树均完全增长，不进行任何修剪，回归树的终止条件为设定好的回归树数量。

第二步：计算特征重要度并排序。

计算随机森林回归模型泛化误差，均方误差MSE如下

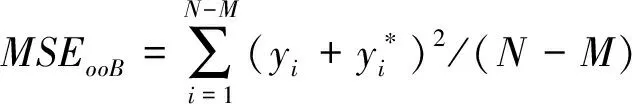
(4)

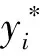
①基于k个训练样本集，构建k棵回归树，并通过预测相对应的测试集得到k个MSE：{M1，M2，…，Mk}。

②通过在k个不同的测试集中随机置换特征Xi产生新的测试集，并用建立好的随机森林模型在新产生的测试集上计算，得到新的MSE，结果如下

(5)

③计算特征重要度分数，将{M1，M2，…，Mk}与新均方误差矩阵第i行相减，得计算特征重要度如下

(6)

式中，Mj为①中计算出的第j个均方误差；Mij为②中计算得出的新均方误差矩阵中的第i行第j个均方误差值；SE为标准差。

④将上述计算得出的重要度分数与查阅的经验知识作为特征重要度评判指标，并筛选出影响地面沉降的关键因素。

2.3 构建基于XGBoost地面沉降预测模型

XGBoost算法[22]是一种设计良好的梯度增强决策树(GBDT)算法，GBDT是一基于集成思想的Boosting学习器，当数据集较大且较为复杂时，运行一次可能需要上千次的迭代，同时GBDT较难实现分布式。而XGBoost能够较好地解决上述问题，具有高效的计算速度，在预测问题中模型表现非常好。在近几年工业领域应用非常的广，并且都取得了很好的效果。XGBoost算法通过建立一系列决策树并为每个叶节点分配一个量化权重来实现对目标变量的估计。预测函数如下

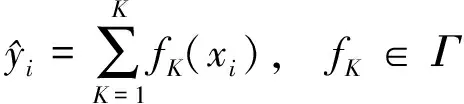
(7)

式中，Γ={f(x)=wq(x)}(q:Rm→T，w∈RT)是由一系列回归树构成的空间；q为每棵树的结构，即每棵树拥有T个叶子节点，每个fK与一棵独立的决策树相对应；w为叶子的权重。为学习模型，权衡模型的复杂程度，XGBoost算法目标函数如下(取目标函数最小值)

(8)

Ω(f)=γT+(λ‖w‖2)/2

(9)

(10)

对损失函数二次泰勒展开有

(11)

式中，gi、hi分别为相互独立的单变量二次函数。通过对候选分割点的估计计算得到最优的权重。

在以上算法原理研究的基础上构建基于XGBoost的地面沉降预测模型。

3 方法实例分析

实例分析所需相关数据由某城市盾构施工工程公司提供，包括盾构开挖过程中某一地层的掘进参数数据和地面沉降监测数据。盾构掘进参数相关数据来自对盾构机各系统实施工况和状态数据采集，地面沉降监测数据来自地面沉降点监测报表。以纵向轴线正上方的监测点为例，共有85个字段，其中，掘进相关数据75列，地面沉降量相关数据10列。按照距轴线距离0 m和开挖面距离(0，3，5，10，15，20，-5，-10，-15，-20环)构建数据包，共可得到 10个数据包用于地面沉降量预测。每个数据包数据样本按4∶1的比例进行划分，其中掘进参数为地面沉降关键影响因素。与训练样本不同的是，验证数据无掘进参数所对应的地面沉降量，其中，训练集用来进行地面沉降量预测模型训练，测试集用来与真实数据集作对比，来验证本文所提出的方法。

3.1 数据包构建结果展示

3.1.1 数据包构建流程

梳理施工安全的数据资源情况，对数据的物理关系、逻辑关系进行分析，并对数据进行预处理，在此基础上构建各类数据包。数据建模流程如图5所示。

图5 数据建模流程

具体步骤如下。

(1)按照距轴线距离初步划分数据包。根据实际项目中横断面地表沉降监测点布置初步划分数据包。

(2)在步骤(1)基础上按照监测点距开挖面距离进一步细化数据包，以坐标的形式准确定位每个地表沉降监测点。

(3)在步骤(2)的基础上，以天为单位，将不同时间点对应的掘进参数数据和地面沉降量数据作为一条数据，这样便可以得到盾构机地面沉降最终数据包。

3.1.2数据包构建结果

根据数据包构建流程，按照每天数据距轴线距离0 m 和开挖面距离(0，3，5，10，15，20，-5，-10，-15，-20环)构建数据包，共可得到10个数据包用于地面沉降量预测，详细数据包构建情况示例如表2所示。

表2 距轴线0 m、距开挖面0环数据包构建结果展示

3.2 地面沉降关键影响因素分析结果展示

3.2.1 地面沉降机理分析

隧道掘进过程中的间隙与超挖现象会导致理论出土量一般情况下小于实际出土量，隧道与衬砌之间会因此产生空隙。空隙的产生会导致盾构周围土体发生流动，从而产生地面沉降。地面沉降的原因一般为土体损失与固结沉降两种。

土体损失指实际出土量与理论出土量的差值，主要分为3类。①正常地层损失：指由于隧道掘进对周围土体产生扰动，从而造成可避免的土体流失。该部分地层损失主要与施工线路的地质情况与施工工艺有关，例如，管片与隧道间空隙产生的沉降等，此种沉降不可避免。②非正常地层损失：指由于盾构机掘进过程中非正常操作导致的地层损失，产生的主要原因有参数设置不当，可能会加速土体扰动，产生更多的非正常地层损失；注浆操作问题，注浆不及时或注浆量不足等问题均会导致土体灌入；纠偏过程中会导致盾体在隧道内发生“摆动”，从而加大隧道与盾体的空隙，产生沉降。③灾害性地层损失：在隧道掘进过程中，遭遇塌方、突水突泥等突发事故从而产生的地层损失。

固结沉降，盾构掘进过程中的超前开挖、挤压与注浆等对地层产生扰动，导致隧道周围产生正负超空隙水压力，从而导致地面沉降。

在盾构掘进过程中，盾构外径、覆土厚度、注浆压力、注浆量、土舱压力、推进速度、千斤顶推力等掘进参数均对地面沉降产生较大影响，如表3所示。

表3 掘进参数与地面沉降的关系

3.2.2 基于随机森林的地面沉降关键影响因素分析

利用随机森林算法对每个数据包进行影响因素提取，以距轴线0 m距开挖面0环、3环、15环为例，影响因素特征提取重要度得分如图6所示。

图6 特征提取重要度得分示例

由图6可知，距轴线0 m情况下，距开挖面0环处共提取得到13个特征，距开挖面3环处共提取得到18个特征，距开挖面5环处共提取得到23个特征，距开挖面10环处共提取得到18个特征，距开挖面15环处共提取得到6个特征，距开挖面20环处共提取得到18个特征，距开挖面-5环处共提取得到9个特征，距开挖面-10环处共提取得到8个特征，距开挖面-15环处共提取得到33个特征，距开挖面-20环处共提取得到22个特征。

综上所述，经过机理知识分析与随机森林选取特征重要度大于10的特征提取后的关键影响因素结果，示例如表4所示。

表4 关键影响因素提取结果示例

3.3 地面沉降预测结果展示

在基于XGBoost的地面沉降预测模型基础上，根据盾构施工实际数据得到距轴线0 m距开挖面0环、3环、5环、10环、15环、20环、-5环、-10环、-15环处、-20环处的预测结果，以0环、3环、20环、-20环为例，如图7所示。

图7 实际数据与预测数据对比示例

综上，各模型的精确度与平均误差如表5所示。

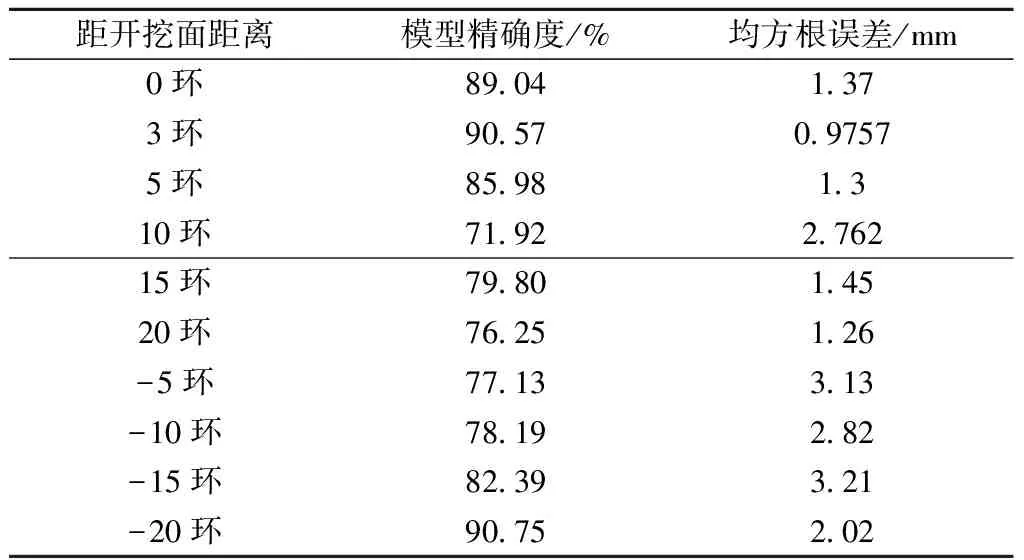
表5 模型的准确度和平均误差

3.4 对比分析

针对上述XGBoost模型的预测结果，分别利用支持向量机(SVR)，AdaBoost回归模型对数据进行预测，以均方根误差(RMSE)为评价指标，并进行对比分析，最终对比分析结果如表6所示。

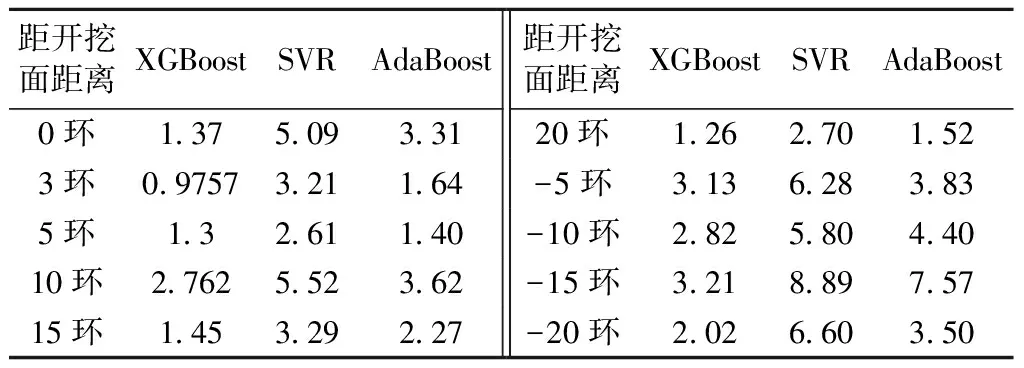
表6 模型均方根误差RMSE对比分析结果

4 结论

针对盾构掘进过程中难以精确预测地面沉降问题，提出一种单一地层地面沉降量的多点预测方法，通过数据挖掘可以得到地面沉降值与盾构机开挖参数值的内在关系。该方法主要创新点如下。

(1)对盾构机开挖前后方不同的环数构建差异化的影响因素分析模型，将提取的差异化关键影响因素集作为XGBoost地面沉降预测模型的输入集，对所设置的10个沉降监测点分别建立预测模型，从而得到多监测点的地面沉降预测值，更为准确地预测施工中的地面沉降量。

(2)基于该方法构建的地表沉降预测模型平均误差在2～3 mm之间，适用于同一地层下的近轴线多点地表沉降量预测，做到对开挖面一定范围内的沉降进行提前准确预测和预警，具备建模简单、准确率较高的优点，为盾构施工过程中安全风险评估提供重要决策。

但对于复杂地层等地表沉降预测问题，该方法缺少研究与案例实证，后续应结合地质参数因素对不同地层的地表沉降量进行模型分析，提高模型的应用广泛性。